空気圧システムにおいて、シリンダースピードが遅い、動作が一定しない、力が不十分であるといったことでお困りではありませんか?これらの一般的な問題は、しばしば誤解された原因である流動抵抗に起因しています。多くのエンジニアは、圧力と力の要件のみに基づいて空気圧コンポーネントのサイズを決定し、実際の性能に及ぼす流体抵抗の重要な影響を見落としています。
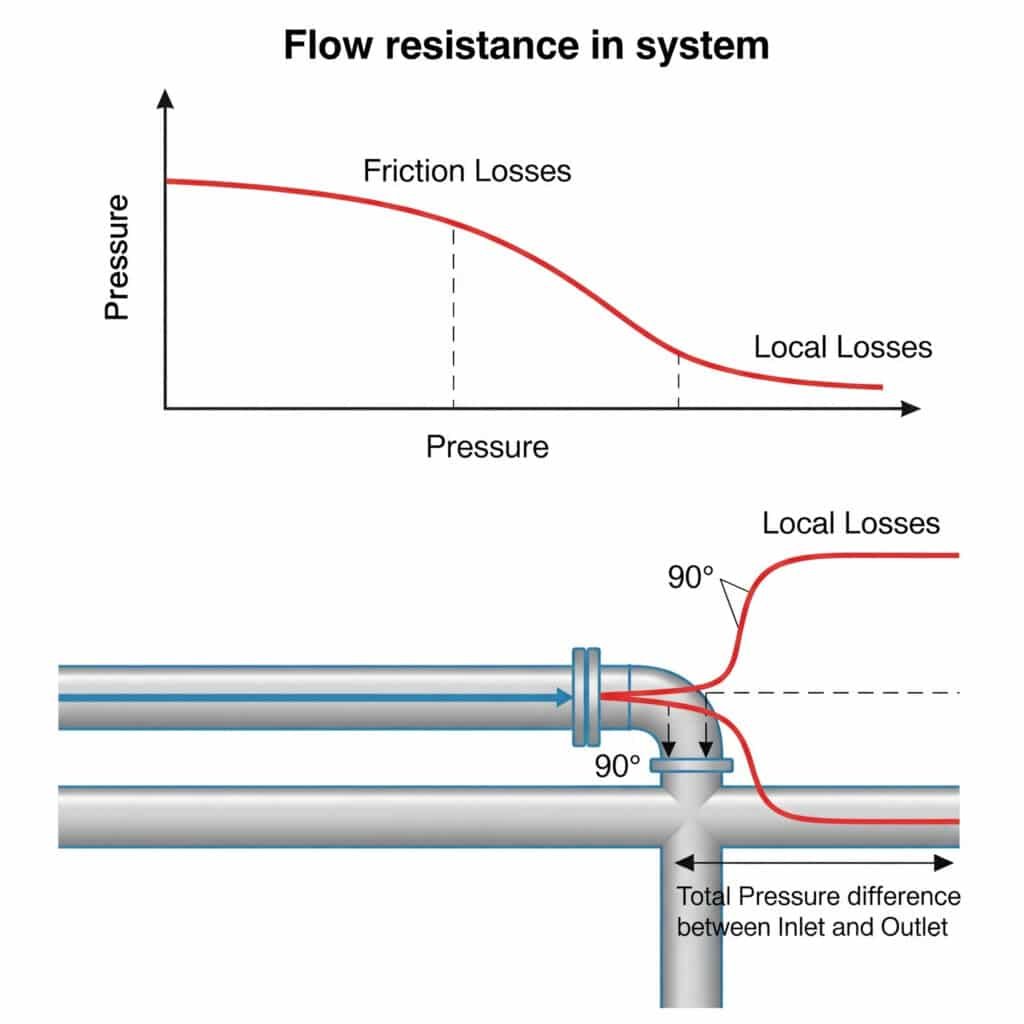
空気圧システムにおける流れの抵抗は、利用可能な力を減少させ、最大速度を制限し、一貫性のない動きを引き起こす圧力低下を生じます。この抵抗は、直管に沿った摩擦(摩擦損失)と継手、ベンド、バルブでの破壊(局所損失)の両方から生じます。これらの抵抗を合わせると、実際のシステム性能は理論計算よりも20-50%低下します。
Beptoで15年以上空気圧システムに携わってきた私は、流動抵抗を理解し対処することで、低性能のシステムが信頼性の高い効率的なオペレーションに変化した事例を数え切れないほど見てきました。これらの隠れたパフォーマンスキラーを計算し、最小化する方法について学んだことをお話しします。
目次
空気圧ラインの摩擦損失はどのように計算するのか?
直管パイプやチューブの摩擦損失は、流体抵抗計算の基礎となるものですが、多くのエンジニアが単純化しすぎた経験則に頼っているため、システムのサイズが過小評価されています。
空気圧ラインの摩擦損失は、次の式で計算される。 ダルシー・ワイスバッハ方程式1ここで、λは摩擦係数、Lはパイプ長、Dはパイプ直径、ρは空気密度、vは流速である。空気圧システムの場合、摩擦係数λは以下に基づいて変化する。 レイノルズ数2 と相対粗さであり、一般的にはルックアップテーブルまたは ムーディー図3.
摩擦損失を理解することは、システム設計やトラブルシューティングに実用的な意味を持つ。これを実用的な洞察に分解してみよう。
摩擦係数表の効果的な使い方
摩擦係数(λ)は圧力損失を計算する上で重要なパラメータですが、その値を決定するには流れの条件を考慮する必要があります:
| フロー・レジーム | レイノルズ数(Re) | 摩擦係数の決定 |
|---|---|---|
| 層流 | Re < 2000 | λ = 64/Re |
| トランジショナル・フロー | 2000 < Re < 4000 | 信頼性に欠ける - この範囲での設計は避けること |
| 乱流 | Re > 4000 | 相対粗さ(ε/D)に基づくルックアップテーブルを使用する。 |
実用摩擦係数ルックアップテーブル
空気圧システムの乱流には、この簡略化した表を使用する:
| パイプ素材 | 相対粗さ(ε/D) | 一般的なレイノルズ数における摩擦係数 (λ) |
|---|---|---|
| Re = 10,000 | ||
| スムース・チューブ(PVC、ポリウレタン) | 0.0001 – 0.0005 | 0.031 |
| アルミニウム・チューブ | 0.001 – 0.002 | 0.035 |
| 亜鉛メッキスチール | 0.003 – 0.005 | 0.042 |
| 錆びた鋼鉄 | 0.01 – 0.05 | 0.054 |
実際の空気圧システムにおける圧力損失の計算
実際の例を見てみよう:
| パラメータ | 値/計算 | 例 |
|---|---|---|
| パイプ径 (D) | 内径 | 8mm (0.008m) |
| パイプの長さ (L) | ストレート全長 | 5m |
| 流量 (Q) | システム要件より | 標準20リットル/秒 |
| 空気密度 (ρ) | 動作圧力時 | 7.2kg/m³(6バール |
| 流速(v) | v = Q/(π×D²/4) | v = 0.02m³/s/(π×0.008²/4) = 398 m/s |
| レイノルズ数(Re) | Re = ρvD/μ | Re = 7.2×398×0.008/1.8×10-⁵ = 1,273,600 |
| 相対粗さ | ポリウレタン・チューブ用 | 0.0003 |
| 摩擦係数 (λ) | ルックアップテーブルより | 0.017 |
| 圧力降下 (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP=0.017×(5/0.008)×(7.2×398²/2)=6.07バール |
実世界での応用シリンダースピードの問題を解決する
昨年、私はウィスコンシン州にある包装機器会社の製造エンジニア、サラと仕事をした。彼女のロッドレスシリンダーシステムは、適切なサイズのシリンダーと十分な供給圧力があるにもかかわらず、期待された速度の60%でしか稼動していませんでした。
彼女のシステムを分析した結果、高流量用途に6mmチューブを使用していることがわかりました。摩擦損失により2.1バールの圧力降下が発生し、使用可能な力と速度が大幅に低下していました。10mmチューブにアップグレードすることで、圧力降下を0.4barに抑えることができました。
実システムにおける摩擦損失の要因
実際の摩擦損失にはいくつかの要因が影響する:
- 気温:高温になると粘度が増し、摩擦が大きくなる
- 汚染:汚れや油分は有効粗さを増加させる
- チューブ曲げ:曲げられたチューブの微小変形が抵抗を増大
- 経年劣化:腐食や付着物が経時的に粗さを増す
- 動作圧力:圧力が高いほど密度が高くなり、損失が増加する。
なぜ等価長法が正確なシステム設計に不可欠なのか?
継手、バルブ、ベンドでの局所的な損失は、直管での摩擦損失を上回ることがよくあるが、多くのエンジニアはそれを無視するか、性能の問題につながる粗雑な見積もり方法を用いている。
等価長さ法は、継手やバルブによる局部的な損失を、同じ圧力損失を引き起こす直管の等価長さに変換する。これはLe = K(D/λ)で計算され、Leは等価長さ、Kは等価長さを表す。 局所損失係数4Dはパイプ径、λは摩擦係数である。この方法は計算を簡素化し、より正確なシステム性能予測を提供する。
この方法を空気圧システム設計に効果的に適用する方法を探ってみよう。
一般的な空圧部品の等価長さ表
一般的な空気圧コンポーネントの実用的な参照表です:
| コンポーネント | K値 | 等価長 (Le/D) |
|---|---|---|
| 90°エルボ(シャープ) | 0.9 | 30 |
| 90°エルボ(標準半径) | 0.3 | 10 |
| 45°エルボ | 0.2 | 7 |
| Tジャンクション(スルーフロー) | 0.3 | 10 |
| Tジャンクション(分岐流) | 1.0 | 33 |
| ボールバルブ(全開) | 0.1 | 3 |
| ゲートバルブ(全開) | 0.2 | 7 |
| クイックコネクトカップリング | 0.4-0.8 | 13-27 |
| 逆止弁 | 1.5-2.5 | 50-83 |
| 標準フローコントロールバルブ | 1.0-3.0 | 33-100 |
等価長法の適用
この方法を効果的に使うために:
- 空気圧回路の全コンポーネントを特定する
- 各コンポーネントのK値または等価長さ比(Le/D)を求める。
- パイプの直径を掛けて等価長さを計算する。
- 等価な長さをすべて、実際の直管の長さに加える。
- 摩擦損失の計算には、有効長の合計を使用する。
例えば、5m の8mm ストレート・チューブに4つの90° エルボー、1つのT字型ジャンクション、2つのクイック・ コネクトを加えたシステム:
| コンポーネント | 数量 | レ/ド | 同等の長さ |
|---|---|---|---|
| 90°エルボ | 4 | 10 | 4 × 10 × 0.008m = 0.32m |
| T字路 | 1 | 10 | 1 × 10 × 0.008m = 0.08m |
| クイックコネクト | 2 | 20 | 2 × 20 × 0.008m = 0.32m |
| 全長 | 0.72m | ||
| 実際のストレートの長さ | 5.00m | ||
| 有効長 | 5.72m |
つまり、5mのシステムは、局所的な損失により、実際には5.72mのシステムのように動作する。
ケーススタディ組立システムにおけるバルブ配置の最適化
私は最近、アリゾナにある電子機器組立工場のオートメーション・エンジニア、ミゲルを手伝った。彼のピックアンドプレースシステムは、高品質の部品を使用しているにもかかわらず、一貫性のない動きとサイクルタイムのばらつきが発生していた。
解析の結果、彼のバルブマニホールドはシリンダーから3m離れており、回路には多数の継手が含まれていることが判明した。等価長計算の結果、実際の距離は3mであったが、局所的なロスにより、有効長は7.2mとなり、直管距離の2倍以上となった!
バルブマニホールドをシリンダーの近くに移設し、いくつかのフィッティングを廃止することで、有効長を7.2mから2.1mに短縮しました。これにより、圧力損失が70%減少し、安定した動作と15%のサイクルタイムの短縮を実現しました。
地元での損失を最小限に抑えるための実践的なヒント
空気圧システムの局所的な損失を低減する:
- スイープエルボーまたはラウンドエルボーを使用する シャープベンドの代わりに(K値を67%下げる)
- 継手の数を最小限に抑える より直接的なルーティングを計画することで
- 摩擦の少ない部品を選ぶ フルボアボールバルブ
- 適切なサイズの継手 - サイズの小さい継手が不均衡な損失を引き起こす
- バルブをアクチュエータの近くに配置する チューブの有効長を最小にする
縮小ボアセクションに空気が流れると何が起こるか?
バルブが部分的に閉じていたり、継手のサイズが小さかったり、直径が変化しているなど、空気圧回路の内径が小さくなっている部分は、システムの性能に重大な影響を与える重大な流量制限を生み出します。
縮径部を空気が流れる場合、 圧力損失5 ΔP=ρ(v₂²-v₁²)/2の式に従って発生し、ここでv₁は制限前の速度、v₂は制限内の速度である。これは、ボア比補正係数C = (1 - (d/D)⁴)を使用して補正することができます。この係数は、実際のシステム性能を予測し、コンポーネントのサイズ不足を避けるのに役立ちます。
ここでは、ボア断面積の減少がもたらす実際的な意味と、システム設計においてそれをどのように考慮すべきかを探ってみよう。
直径遷移における圧力損失の計算
大口径から小口径に空気が流れる場合、圧力損失は次のようにして計算できる:
| パラメータ | フォーミュラ | 例 |
|---|---|---|
| 元の直径 (D) | 仕様書より | 10mm |
| 縮径 (d) | 仕様書より | 6mm |
| ボア比(d/D) | 単純分割 | 0.6 |
| 流量 (Q) | システム要件より | 標準15リットル/秒 |
| 原管内速度 (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| 縮小区間での速度(v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| 圧力降下 (ΔP) | ΔP = ρ(v₂ - v₁²)/2 | 0.88バール |
| 補償係数(C) | C = (1 - (d/D)⁴) | 0.87 |
一般的な口径縮小シナリオとその影響
ここでは、口径の減少が流量にどのように影響するかを説明する:
| ボア減少 | フロー容量削減 | 圧力降下の増加 |
|---|---|---|
| 10mm~8mm | 36% | 2.4× |
| 10mm~6mm | 64% | 7.7× |
| 10mm~4mm | 84% | 39× |
| 8mmから6mm | 44% | 3.2× |
| 8mm~4mm | 75% | 16× |
| 6mmから4mm | 56% | 5.1× |
これらの数値は、一見小さな直径の縮小がシステム性能に劇的な影響を及ぼす理由を浮き彫りにしている。
複数の制限の累積効果
実際の空気圧回路では、複数の制限が直列に発生します。それらの効果は累積的であり、以下を使用して計算できます:
- 各制限を等価なCファクターに変換する。
- トータルCファクターを計算する:Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- この合計係数を使用して、システム全体の性能低下を決定する。
ケーススタディバルブとアクチュエータのミスマッチ問題の解決
先月、私はノースカロライナ州にある家具製造工場のメンテナンス・スーパーバイザー、トーマスと仕事をした。彼の新しいロッドレスシリンダーシステムは、メーカーが推奨するバルブサイズを使用しているにもかかわらず、予想される速度の半分以下で稼動していた。
調査の結果、彼のサーキットに複数のボア減少があることが判明した:
- 10mm供給ラインから8mmバルブポートへ(C₁=0.36)
- 8mmバルブポート~6mmフィッティング(C₂ = 0.44)
- 6mm継手、8mmシリンダーポート、内部制限あり(C₃ = 0.32)
総補償係数はCtotal = 1 - (1-0.36)(1-0.44)(1-0.32) = 0.75で、彼のシステムは理論流量の75%を失っていたことになる!
システム全体を適切なサイズの部品にアップグレードすることで、こうした制約をなくし、シリンダーや供給圧力を変えることなく、要求される性能を達成しました。
ボア減少ロスを最小限に抑える実践的戦略
ボア減少による損失を減らす:
- 部品のサイズを一定にする 空気回路全体
- 実用的な最大サイズのチューブを使用する 高流量用
- 内部コンポーネントの制限に注意接続サイズだけでなく
- 平行流路を考える 大流量が必要な場合
- 不要なアダプターやトランジションを排除 可能な限り
空気圧システムにおける「最弱リンク」の原則
空気圧システムの性能は、最も制限の多いコンポーネントによって制限されることを忘れないでください。サイズが小さいエレメントが1つあると、システム内の他の場所にある適切なサイズのコンポーネントの利点が無効になる可能性があります。
例えば、10mmチューブ、10mmバルブ、シリンダー部の6mmフィッティングのシステムは、全体が6mmコンポーネントのシステムと基本的に同じ性能を発揮するが、コストは高くなる。
結論
摩擦係数表、等価長さ法、縮径補正法など、流動抵抗を理解し、適切に計算することは、実環境で期待通りの性能を発揮する空圧システムを設計するために不可欠です。これらの計算方法と設計原則を適用することで、ロッドレスシリンダアプリケーションやその他の空圧システムを最適化し、最大の性能と信頼性を得ることができます。
空気圧システムの流動抵抗に関するFAQ
空気圧システムで許容できる圧力損失はどのくらいですか?
許容可能な圧力損失はアプリケーションの要件によって異なりますが、一般的なガイドラインとして、効率的な運転のためには、総圧力損失を供給圧力の10~15%に制限してください。6バールのシステムの場合、これは総圧力損失を0.6~0.9バール以下に抑えることを意味します。重要な用途では、安定した性能を維持するために、5~8%というさらに低い圧力降下が必要になる場合があります。
チューブ径と圧力損失の関係は?
空気圧システムの乱流では、圧力損失は直径(D⁵)の5乗に反比例する。つまり、チューブの直径を2倍にすると、圧力損失は約32分の1になります。例えば、6mmから12mmにチューブを太くすると、同じ流量条件下で圧力損失が1.5 barからわずか0.047 barに減少します。
空気圧用途に適したチューブサイズはどのように決めればよいですか?
流量要件と許容可能な圧力損失に基づいてチューブサイズを選択する。レイノルズ数と摩擦係数を計算し、ダルシー・ワイスバッハ方程式を使用して異なる直径の圧力損失を求めます。スペースの制約とコストを考慮しながら、圧力損失を許容範囲内(通常は供給圧力の<10%)に抑える最小径を選択します。
90°エルボと5メートルのストレートチューブ、どちらがより大きな制限を作るか?
鋭利な90°エルボは通常、直管チューブの直径30本分に相当する抵抗を生じさせます。8mmチューブの場合、鋭利なエルボ1個は約240mm (30 × 8mm)のストレート・チューブに相当します。つまり、5メートルのストレート・チューブは、エルボ1個 の約21倍の抵抗を生み出すことになる。しかし、シス テムには複数のエルボや継手が含まれることが多く、そ れらの累積効果が直管長を上回ることもある。
クイック・コネクト・フィッティングはシステム性能にどのような影響を与えますか?
標準的なクイック・コネク ト・フィッティングは、通常、直管チューブの直径 15 ~ 25 に相当する局部的な損失をもたらします。さらに重大な点として、多くのクイックコネク トは、公称サイズよりも小さな内部制限を有してい る。10mm "のクイックコネク トは、わずか7-8mmの内部制限を持つ場合があ り、その時点で50-70%の流量容量を減少 させる内径減少を生じさせる。
流量制御弁の一部閉鎖がシステム性能に与える影響は?
流量制御弁を全口径の50%まで閉じた場合、50%だけ流量が減少するのではなく、口径と流量容量の間の非線形関係により、約75%だけ流量が減少します。圧力損失は流速変化の二乗に従って増加するので、有効直径を半分にすると、同じ流量条件下で圧力損失は約16倍に増加する。
-
ダルシー・ワイスバッハ方程式は、流体力学において、パイプ内の摩擦による圧力損失を計算するための基本的かつ広く使用されている式である。 ↩
-
レイノルズ数の明確な定義を提供。レイノルズ数は、さまざまな流体流動状況における流動パターン(層流または乱流)を予測するために使用される重要な無次元量である。 ↩
-
ダルシー摩擦係数をレイノルズ数と相対粗さに対してプロットした包括的なグラフであるムーディー・ダイアグラムを紹介。これは、エンジニアがパイプ内の圧力損失を決定するための標準的なツールである。 ↩
-
等価長法の一部として配管継手やバルブの圧力損失を特徴付けるために使用される無次元数であるK値(局所損失係数)の概念について説明。 ↩
-
流体が制限(オリフィス)を通過する際に生じる圧力損失の背後にある物理学について、連続方程式とベルヌーイの原理の原則に基づいて詳述。 ↩




