
を触ったことがあるだろうか? 空気圧シリンダー 連続運転の後、その熱さに驚きましたか?その熱さは単なる不便さではなく、エネルギーの浪費、効率の低下、潜在的な信頼性の問題を表しており、あなたのオペレーションに何千ドルもの損失を与えている可能性があります。
空気圧システムにおける熱伝達は、部品材料を介した伝導、表面と空気間の対流、高温の表面からの放射という3つのメカニズムで発生します。これらの原理を理解し最適化することで、動作温度を15-30%低下させ、部品寿命を最大40%延長し、エネルギー効率を5-15%向上させることができます。
先月、私はジョージア州のある食品加工工場のコンサルティングを行った。そこでは、ロッドレスシリンダーが熱の問題で3~4カ月ごとに故障していた。メンテナンス・チームは、根本的な原因に対処することなく、単に部品を交換していました。適切な伝熱原理を適用することで、作動温度を22℃下げ、部品の寿命を1年以上に延ばしました。私たちがどのようにそれを実現したのか、そして、同じ原理をあなたのシステムにどのように適用できるのか、お見せしましょう。
目次
- 伝導率の計算:熱は部品の中をどのように移動するか?
- 対流強化法:空気から表面への熱伝達を最大化する手法とは?
- 放射効率モデル:空気圧システムにおいて熱放射が問題となるのはどのような場合か?
- 結論
- 空気圧システムの熱伝達に関するFAQ
伝導率の計算:熱は部品の中をどのように移動するか?
伝導は、固体空気圧コンポーネント内の主要な熱伝達メカニズムです。伝導係数を計算し、最適化する方法を理解することは、システム温度を管理するために不可欠です。
熱伝導率は次の式で計算できる。 フーリエの法則1ここで、qは熱流束(W/m²)、kは熱伝導率(W/m・K)、dT/dxは温度勾配である。空気圧部品の場合、効果的な伝導は、材料の選択、界面の品質、および熱経路の長さと断面積に影響する幾何学的要因に依存します。
テネシー州の製造ラインで、ロッドレスシリンダーのベアリングが早期に破損するトラブルシューティングを行ったことを覚えている。メンテナンスチームは複数の潤滑剤を試しましたが、うまくいきませんでした。伝導経路を分析したところ、ベアリングとハウジングの界面に熱のボトルネックがあることがわかりました。表面仕上げを改善し、熱伝導性コンパウンドを塗布することで、有効伝導係数を340%増加させ、不具合を完全に解消しました。
基本伝導方程式
空気圧部品の伝導を計算するための主要な方程式を分解してみよう:
熱伝導に関するフーリエの法則
熱伝導を支配する基本方程式は次の通りである:
q = -k(dT/dx)
どこでだ:
- q = 熱流束 (W/m²)
- k = 熱伝導率 (W/m-K)
- dT/dx = 温度勾配(K/m)
断面が一定の単純な一次元の場合:
Q = kA(T₁-T₂)/L
どこでだ:
- Q = 熱伝達率(W)
- A = 断面積 (m²)
- T₁、T₂=両端の温度(K)
- L = ヒートパスの長さ(m)
熱抵抗の概念
複雑な形状の場合、熱抵抗アプローチの方が実用的であることが多い:
R = L/(kA)
どこでだ:
- R = 熱抵抗(K/W)
複数のコンポーネントを直列に接続したシステムの場合:
Rtotal = R₁ + R₂ + R₃ + ... + Rm_2099
そして熱伝達率はこうなる:
Q = ΔT/Rtotal
材料の熱伝導率の比較
| 素材 | 熱伝導率 (W/m-K) | 相対導電率 | 一般的なアプリケーション |
|---|---|---|---|
| アルミニウム | 205-250 | 高い | シリンダー、ヒートシンク |
| スチール | 36-54 | ミディアム | 構造部品 |
| ステンレス鋼 | 14-16 | ロー・ミディアム | 腐食性環境 |
| ブロンズ | 26-50 | ミディアム | ベアリング、ブッシュ |
| PTFE | 0.25 | 非常に低い | シール、ベアリング |
| ニトリルゴム | 0.13 | 非常に低い | Oリング、シール |
| 空気(静止) | 0.026 | 極めて低い | 隙間埋め |
| サーマルペースト | 3-8 | 低い | インターフェイス素材 |
空気圧アセンブリの接触抵抗
部品間の界面では、接触抵抗が熱伝導に大きく影響する:
Rcontact = 1/(hc × A)
どこでだ:
- hc = 接触係数 (W/m²-K)
- A = 接触面積 (m²)
接触抵抗に影響を与える要因には、以下のようなものがある:
- 表面粗さ:粗い表面は実際の接触面積が少ない。
- コンタクト・プレッシャー:圧力が高いほど有効接触面積が増える
- インターフェイス材料:サーマル・コンパウンドが隙間を埋める
- 表面清浄度:汚染物質が抵抗性を高める
ケーススタディロッドレスシリンダーの熱最適化
熱問題が発生している磁気ロッドレスシリンダー用:
| コンポーネント | オリジナル・デザイン | 最適化されたデザイン | 改善 |
|---|---|---|---|
| シリンダーボディ | 陽極酸化アルミニウム | 同素材で仕上げが向上 | 15%より優れた伝導性 |
| ベアリング・インターフェース | 金属同士の接触 | サーマルコンパウンドの追加 | 340% より良い伝導 |
| 取付ブラケット | 塗装スチール | ベアアルミニウム | 280% より良い伝導 |
| 全体的な熱抵抗 | 2.8 K/W | 0.7 K/W | 75%リダクション |
| 動作温度 | 78°C | 56°C | 22℃低減 |
| 部品寿命 | 4ヶ月 | >12ヶ月以上 | 3倍向上 |
実用的な伝導最適化技術
何百もの空気圧システムに携わってきた私の経験に基づき、導通を改善するための最も効果的なアプローチをご紹介します:
インターフェイスの最適化
- 表面仕上げ:Ra0.4~0.8μmまで相手表面の平滑性を向上。
- 熱インターフェース材料2:適切なコンパウンドを塗布する(3~8W/m・K)
- ファスナートルク:最適な接触圧を得るために適切な締め付けを行うこと
- 清潔さ:組み立ての前に、すべての油と汚染物質を取り除く
材料選択戦略
- クリティカル・ヒート・パス:導電性の高い材料を使用する(アルミニウム、銅)
- サーマルブレイク:熱を遮断するために、意図的に導電性の低い素材を使用する。
- 複合アプローチ:最適なパフォーマンスとコストのために素材を組み合わせる
- 異方性材料:適切な場合には指向性伝導率を利用する
幾何学的最適化
- ヒートパスの長さ:熱源とシンク間の距離を最小にする
- 断面積:熱の流れに垂直な面積を最大にする
- 熱ボトルネック:熱経路の狭窄を特定し、取り除く
- 冗長パス:複数の平行伝導ルートを作る
対流強化法:空気から表面への熱伝達を最大化する手法とは?
空気圧システムの冷却において、対流はしばしば制限要因となります。対流熱伝達を強化することで、熱管理とシステム性能を劇的に向上させることができます。
対流熱伝導は以下の通りである。 ニュートンの冷却の法則3:ここで、hは対流係数(W/m²・K)、Aは表面積、(Ts-T∞)は表面と流体の温度差である。強化方法には、フィンによる表面積の増加、指向性気流による流体速度の向上、乱流境界層を促進するための表面特性の最適化などがある。
アリゾナ州にある包装施設のエネルギー効率監査で、私は43℃の周囲環境で稼動している空気圧システムに遭遇しました。ロッドレスシリンダーは、メンテナンス要件をすべて満たしているにもかかわらず、オーバーヒートしていました。小型のアルミフィンと低電力ファンを追加することで、対流係数を450%増加させました。これにより、システムを大きく変更することなく、運転温度を危険なレベルから仕様の範囲内まで下げることができました。
対流熱伝達の基礎
対流熱伝達を支配する基本方程式は次の通りである:
Q = hA(Ts-T∞)
どこでだ:
- Q = 熱伝達率(W)
- h = 対流係数 (W/m²-K)
- A = 表面積 (m²)
- Ts = 表面温度 (K)
- T∞ = 流体(空気)の温度(K)
対流係数hは複数の要因に依存する:
- 流体特性(密度、粘度、熱伝導率)
- 流れの特性(流速、乱流)
- 表面の形状と向き
- 流れレジーム(自然対流と強制対流)
自然対流と強制対流
| パラメータ | 自然対流 | 強制対流 | 意味合い |
|---|---|---|---|
| 典型的なh値 | 5-25 W/m²-K | 25-250 W/m²-K | 強制対流は10倍の効果がある |
| 原動力 | 浮力(温度差) | 外圧(ファン、ブロワー) | 強制対流は温度への依存度が低い |
| フローパターン | 表面に沿った垂直方向の流れ | 強制メカニズムに基づく方向性 | 強制フローは特定の部品に最適化できる |
| 信頼性 | 受動的、常に存在する | 電源とメンテナンスが必要 | 自然対流によるベースライン冷却 |
| スペース要件 | 空気循環のためのクリアランスが必要 | エアムーバーとダクト用のスペースが必要 | 強制システムはより計画的でなければならない |
対流強化テクニック
表面積拡大
有効表面積を増やす
フィンとエクステンド・サーフェス
- ピンフィン:全方向エアフロー、150-300%面積増加
- プレートフィン:指向性エアフロー、200-500%面積増加
- 波形表面:中程度の強化、50-150%面積増加表面粗面化
- マイクロテクスチャ加工:5-15%の有効面積増加
- ディンプル表面:10-30%の増加と境界層効果
- 溝付きパターン:15-40%は、方向性の利点を持つ増加
フロー操作
気流特性の改善
強制空気システム
- ファン:指向性気流、200-600% h改善
- ブロワ高圧フロー、300-800% h改善
- 圧縮空気ジェット:ターゲット冷却、400-1000%局所時間改善フローパスの最適化
- バッフル:重要部品に直接空気を送る
- ベンチュリー効果:特定の表面で空気を加速させる
- 渦発生装置:境界層を乱す乱流を発生
表面の修正
対流を促進するために表面特性を変える:
放射率治療
- ブラックオキサイド:放射率を0.7~0.9に高める。
- 陽極酸化処理:放射率を0.4~0.9に制御
- 塗料とコーティング最大0.98までカスタマイズ可能な放射率濡れ性コントロール
- 親水性コーティング:液体冷却の強化
- 疎水性の表面:結露の問題を防ぐ
- パターン化された濡れ性凝縮水の流れ
実施例
高温環境で使用されるロッドレス空圧シリンダー用:
| 強化メソッド | 実施 | h改善 | 温度低減 |
|---|---|---|---|
| ピンフィン(6mm) | アルミニウム製クリップオンフィン、10mm間隔 | 180% | 12°C |
| ダイレクト・エアフロー | 80mm、2W DCファン(1.5m/秒 | 320% | 18°C |
| 表面処理 | ブラックアルマイト | 40% | 3°C |
| 複合アプローチ | すべての方法を統合 | 450% | 24°C |
設計計算のためのヌッセルト数相関
工学的な計算では ヌッセルト数4 (Nu)は対流に対する無次元的なアプローチを提供する:
Nu = hL/k
どこでだ:
- L = 特性長
- k = 流体の熱伝導率
平板上の強制対流の場合:
Nu = 0.664Re^(1/2)Pr^(1/3) (層流)
Nu = 0.037Re^(4/5)Pr^(1/3) (乱流)
どこでだ:
- Re = レイノルズ数(速度×長さ×密度/粘度)
- Pr = プランドル数(比熱×粘度/熱伝導率)
これらの相関関係により、エンジニアはさまざまな構成の対流係数を予測し、それに応じて冷却戦略を最適化することができる。
放射効率モデル:空気圧システムにおいて熱放射が問題となるのはどのような場合か?
空気圧システムの熱管理において、輻射は見過ごされがちですが、多くのアプリケーションにおいて、輻射は全熱伝達の15-30%を占めることがあります。放射熱伝達を最適化するタイミングと方法を理解することは、包括的な熱管理にとって非常に重要です。
輻射熱伝達は次の式に従う。 ステファン・ボルツマンの法則5:Q=εσA(T₁⁴-T₂⁴)、ここでεは表面放射率、σはステファン-ボルツマン定数、Aは表面積、T₁とT₂は放射表面と周囲の絶対温度である。空気圧システムにおける放射効率は、主に表面放射率、温度差、およびコンポーネントとその環境との間の視界要因に依存する。
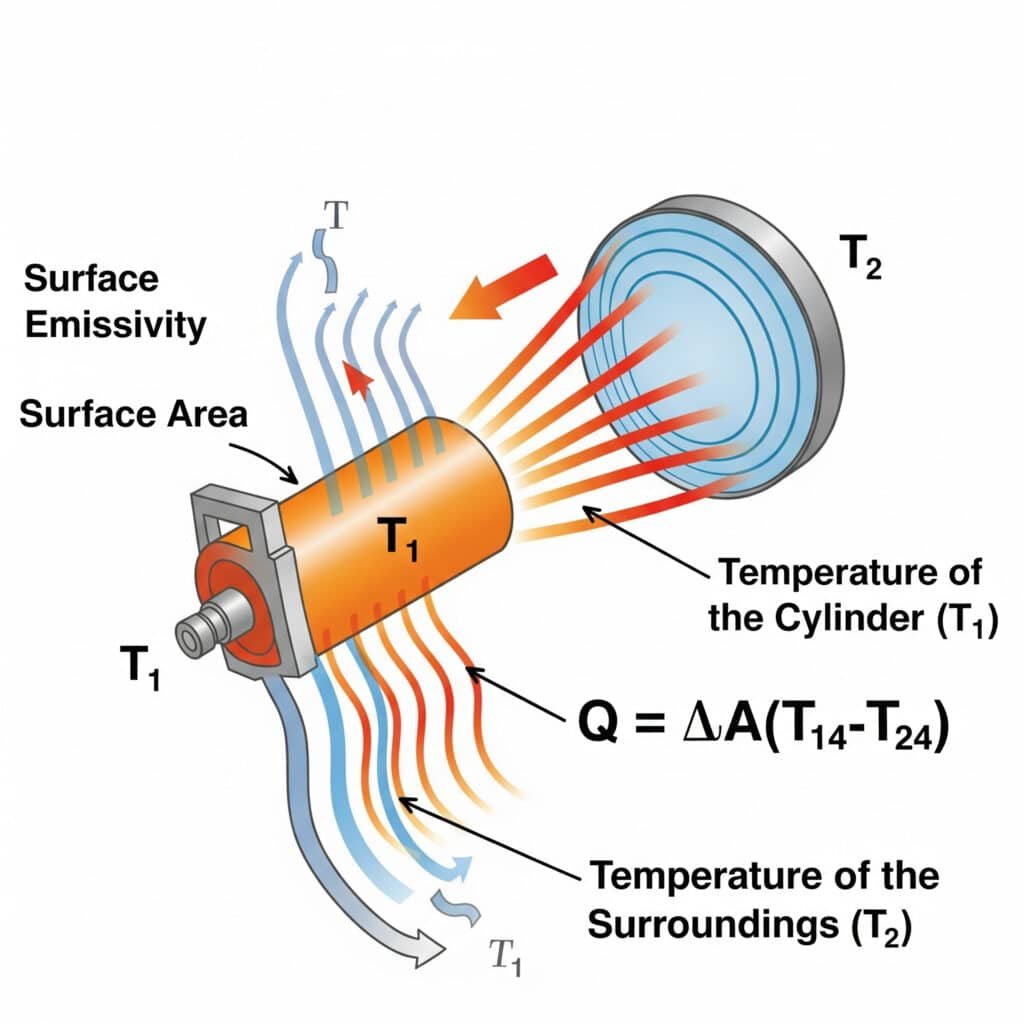
私は最近、オレゴン州にある半導体製造装置メーカーの精密ロッドレスシリンダーの過熱問題を解決する手助けをした。同社のエンジニアは、伝導と対流にばかり注目していたが、放射を見落としていた。高放射率コーティング(εを0.11から0.92に増加)を施すことで、放射熱伝達を700%以上向上させました。このシンプルでパッシブなソリューションにより、可動部品やエネルギー消費なしに動作温度を9℃下げることができました。
放射伝熱の基礎
放射熱伝達を支配する基本方程式は次の通りである:
Q = εσA(T₁⁴-T₂⁴)
どこでだ:
- Q = 熱伝達率(W)
- ε = 放射率(無次元、0-1)
- σ = ステファン・ボルツマン定数 (5.67 × 10-⁸ W/m²-K⁴)
- A = 表面積 (m²)
- T₁ = 表面絶対温度(K)
- T₂=周囲の絶対温度(K)
一般的な空気圧材料の表面放射率値
| 素材/表面 | 放射率 (ε) | 放射効率 | 強化の可能性 |
|---|---|---|---|
| ポリッシュド・アルミニウム | 0.04-0.06 | 非常に悪い | >1500%改善可能 |
| 陽極酸化アルミニウム | 0.7-0.9 | 素晴らしい | すでに最適化されている |
| ステンレススチール(ポリッシュ仕上げ) | 0.07-0.14 | 貧しい | >600%改善可能 |
| ステンレススチール(酸化処理) | 0.6-0.85 | グッド | 中程度の改善の可能性 |
| スチール(ポリッシュ仕上げ) | 0.07-0.10 | 貧しい | >900%改善可能 |
| スチール(酸化処理) | 0.7-0.9 | 素晴らしい | すでに最適化されている |
| 塗装面 | 0.8-0.98 | 素晴らしい | すでに最適化されている |
| PTFE(白) | 0.8-0.9 | 素晴らしい | すでに最適化されている |
| ニトリルゴム | 0.86-0.94 | 素晴らしい | すでに最適化されている |
ファクターに関する考察
放射交換は放射率だけでなく、表面間の幾何学的関係にも依存する:
F₁₂=表面1を出た放射線のうち表面2に当たる割合
複雑な形状の場合、ビューファクターは次のようにして計算できる:
- 分析ソリューション 単純な形状の場合
- 因子代数を表示 既知の解を組み合わせるための
- 数値手法 複雑な手配の場合
- 経験的近似値 実践的エンジニアリングのために
放射線の温度依存性
4乗の温度関係により、放射線は特に高温で効果を発揮する:
| 表面温度 | 放射*による熱伝達の割合 |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*自然対流条件、ε=0.8、周囲温度25℃を想定
放射線効率向上戦略
産業用空気圧システムに関する私の経験に基づき、輻射熱伝達を改善するための最も効果的なアプローチを紹介します:
表面放射率の修正
高放射率コーティング
- アルミニウム用黒アルマイト処理(ε≒0.8~0.9)
- スチール用黒色酸化物 (ε≈ 0.7-0.8)
- 特殊セラミックコーティング (ε≈ 0.9-0.98)表面のテクスチャリング
- 微細粗面化により実効放射率を向上
- 多孔質表面は放射特性を高める
- 放射率/対流強化の組み合わせ
環境最適化
周囲の温度管理
- 高温の機器/プロセスからの遮蔽
- 壁や天井を冷やして放射交換を改善
- 放射線をより涼しい表面に導く反射バリアファクター改善を見る
- 涼しい表面に最大限触れるような向き
- 障害物の除去
- 涼しい地域との放射線交換を改善する反射板
ケーススタディ精密空気圧における放射線強化
クリーンルーム環境での高精度ロッドレスシリンダー用:
| パラメータ | オリジナル・デザイン | 放射線強調設計 | 改善 |
|---|---|---|---|
| 表面素材 | ポリッシュ・アルミニウム(ε≒0.06) | セラミック・コーティング・アルミニウム(ε≒0.94) | 1467%の放射率の増加 |
| 放射熱伝達 | 2.1W | 32.7W | 1457%放射線の増加 |
| 動作温度 | 68°C | 59°C | 9℃低下 |
| 部品寿命 | 8ヶ月 | >24カ月以上 | 3倍向上 |
| 実施コスト | – | $175/シリンダー | 4.2ヶ月の投資回収 |
放射と他の熱伝達モード
効率的な熱管理には、いつ放射が優勢になるかを理解することが重要である:
| コンディション | 伝導優位 | 対流優位 | 放射線支配 |
|---|---|---|---|
| 温度範囲 | 低い方から高い方へ | 低~中 | 中~高 |
| 材料特性 | 高誘電率素材 | 低k、高表面積 | 高εサーフェス |
| 環境要因 | 良好な熱接触 | 動く空気、ファン | 大きな温度差 |
| スペースの制約 | 厳重な梱包 | オープンエアフロー | 涼しい周囲の眺め |
| ベストアプリケーション | コンポーネント・インターフェース | 一般冷却 | 熱い表面、真空、静止空気 |
結論
伝導係数計算、対流促進法、放射効率モデリングなど、熱伝導の原理をマスターすることは、空気圧システムにおける効果的な熱管理の基礎を提供します。これらの原理を応用することで、厳しい環境下でも信頼性の高い動作を保証しながら、動作温度を下げ、部品の寿命を延ばし、エネルギー効率を向上させることができます。
空気圧システムの熱伝達に関するFAQ
運転中の空気圧シリンダーの典型的な温度上昇は?
空気圧シリンダーは通常、連続運転中に周囲温度より20~40℃上昇する。この上昇は、シールとシリンダー壁の摩擦、空気の圧縮加熱、機械的な仕事が熱に変換されることに起因する。ロッドレスシリンダーは、より複雑なシールシステムとベアリング/シールアセンブリでの集中的な発熱により、より高い温度上昇(30~50℃)を経験することがよくあります。
作動圧力は空気圧システムの発熱にどのように影響しますか?
作動圧力は発熱に大きな影響を与え、圧力が高いほど、いくつかのメカニズムによってより多くの熱が発生します。作動圧力が1bar上がるごとに、シールと表面間の摩擦力が大きくなり、圧縮発熱が大きくなり、漏れに関連する損失が増加するため、発熱量は通常8-12%増加します。この関係は、通常の運転範囲(3~10 bar)ではほぼ直線的です。
さまざまな環境における空圧部品の最適な冷却方法とは?
クリーンな中温環境(15~30℃)では、適切な部品間隔による自然対流で十分な場合が多い。高温環境(30~50℃)では、ファンや圧縮空気による強制対流が必要になる。極端に高温の環境(50℃以上)や空気の流れが制限される場所では、サーモエレクトリック・クーラーや液冷のような能動的な冷却方法が必要になる場合があります。いずれの場合も、高放射率表面による放射を最大化することで、さらに受動的な冷却が可能になります。
空気圧部品からの全熱伝達はどのように計算するのですか?
各機構からの寄与を合計して全熱伝導を計算する:Qtotal = Qconduction + Qconvection + Qradiation。伝導については、各熱経路について Q = kA(T₁-T₂)/L を用いる。対流については、Q = hA(Ts-T∞) と適切な対流係数を用いる。放射については、Q = εσA(T₁⁴-T₂⁴) を使用する。30~80℃で作動するほとんどの産業用空気圧アプリケーションでは、おおよその分布は、20~40%伝導、40~70%対流、および10~30%放射である。
温度と空気圧機器の寿命の関係は?
部品の寿命は、温度が上昇するにつれて指数関数的に減少し、アレニウスの関係が修正されます。経験則として、使用温度が10℃上昇するごとに、シールとコンポーネントの寿命は40~50%短くなります。つまり、70℃で作動する部品は、50℃で作動する同じ部品の3分の1しか持たない可能性があるということです。この関係は、シール、ベアリング、ガスケットのようなポリマー部品にとって特に重要で、空気圧システムのメンテナンス間隔を決定することがよくあります。
-
熱伝導率と温度勾配に基づき、固体物質を通して熱がどのように伝導するかを説明する基本原理であるフーリエの法則について、基礎的な解説を行う。 ↩
-
熱伝導を改善し、熱抵抗を低減するために部品間の微細な空隙を埋めるために使用されるサーマルインターフェイス材料(TIM)の機能と種類を説明。 ↩
-
システム冷却設計の重要な要素である、対流によって周囲の流体に熱を伝えることで物体が冷却される仕組みを支配するニュートンの冷却法則の原理について詳しく説明します。 ↩
-
流体力学と伝熱における重要な無次元量であるヌッセルト数について詳しく解説。ヌッセルト数は、境界を介した対流熱伝達と伝導熱伝達の比を表す。 ↩
-
黒体から放射される全エネルギーを定量化する基本的な物理原理であるステファン・ボルツマンの法則について解説。 ↩


