공압 시스템의 느린 실린더 속도, 일관되지 않은 동작 또는 불충분한 힘으로 인해 어려움을 겪고 계신가요? 이러한 일반적인 문제는 종종 잘못 알려진 원인인 유량 저항에서 비롯됩니다. 많은 엔지니어가 압력과 힘 요구 사항만을 기준으로 공압 부품의 크기를 정하고, 유량 저항이 실제 성능에 미치는 중대한 영향을 간과합니다.
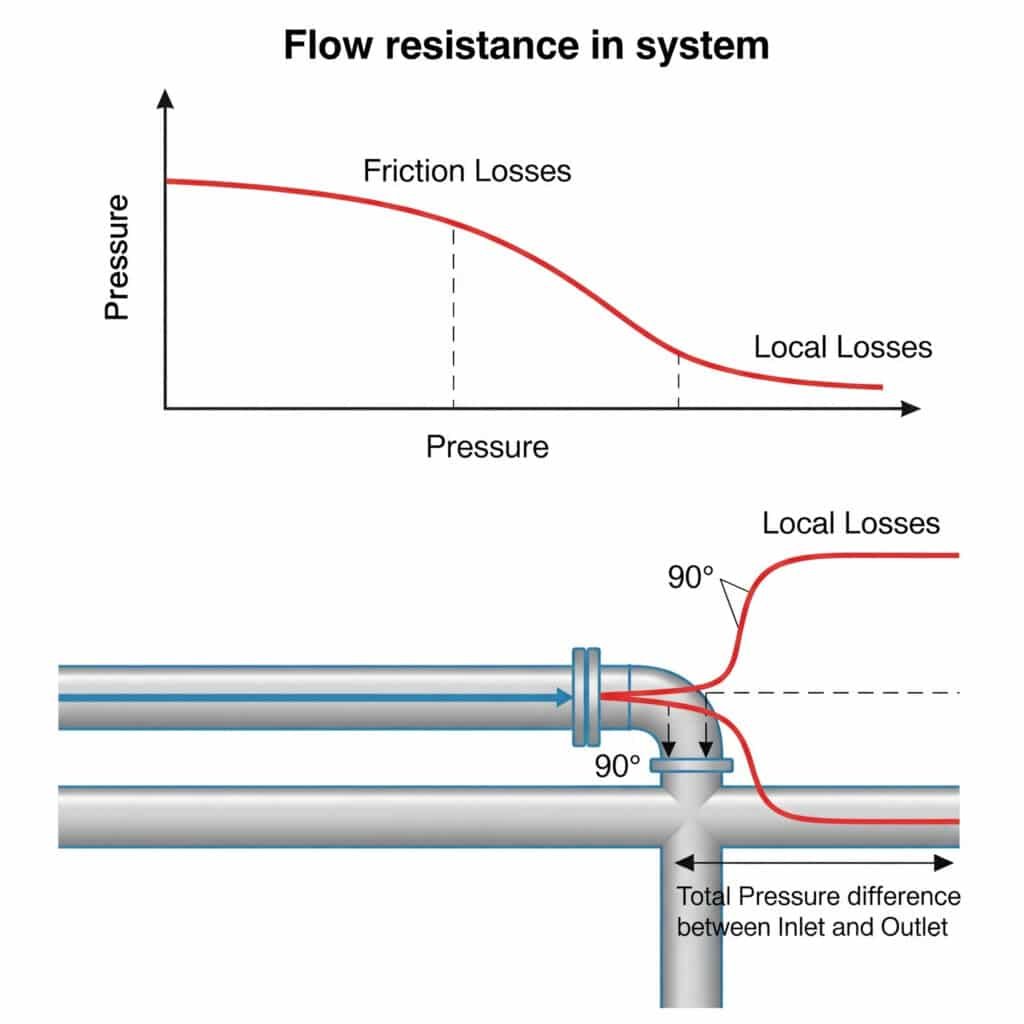
공압 시스템의 흐름 저항은 압력 강하를 발생시켜 사용 가능한 힘을 감소시키고 최대 속도를 제한하며 일관되지 않은 동작을 유발합니다. 이러한 저항은 직선 파이프를 따라 발생하는 마찰(마찰 손실)과 피팅, 굽힘 및 밸브에서의 중단(국부적 손실) 모두에서 발생합니다. 이러한 저항이 합쳐지면 이론적 계산에 비해 실제 시스템 성능이 20~50% 감소할 수 있습니다.
벱토에서 15년 이상 공압 시스템을 다루면서 유량 저항을 이해하고 해결함으로써 성능이 저하된 시스템을 안정적이고 효율적인 운영으로 전환한 사례를 수없이 많이 보았습니다. 이러한 숨겨진 성능 저하 요인을 계산하고 최소화하는 방법에 대해 제가 배운 것을 공유하겠습니다.
목차
- 공압 라인의 마찰 손실은 실제로 어떻게 계산할 수 있을까요?
- 등가 길이 방식이 정확한 시스템 설계에 중요한 이유는 무엇인가요?
- 축소된 보어 섹션을 통해 공기가 흐르면 어떻게 될까요?
- 결론
- 공압 시스템의 유량 저항에 대한 FAQ
공압 라인의 마찰 손실은 실제로 어떻게 계산할 수 있을까요?
직선 파이프와 튜브의 마찰 손실은 유량 저항 계산의 기초이지만, 많은 엔지니어가 지나치게 단순화된 경험 법칙에 의존하여 시스템 크기를 잘못 계산하는 경우가 많습니다.
공압 라인의 마찰 손실은 다음을 사용하여 계산됩니다. 다아시-바이스바흐 방정식1ΔP = λ(L/D)(ρv²/2), 여기서 λ는 마찰 계수, L은 파이프 길이, D는 파이프 직경, ρ는 공기 밀도, v는 유속입니다. 공압 시스템의 경우 마찰 계수 λ는 다음에 따라 달라집니다. 레이놀즈 수2 및 상대적 거칠기이며, 일반적으로 조회 테이블이나 무디 다이어그램3.
마찰 손실을 이해하는 것은 시스템 설계와 문제 해결에 실질적인 영향을 미칩니다. 이를 실행 가능한 인사이트로 세분화해 보겠습니다.
마찰 계수 테이블을 효과적으로 사용하기
마찰 계수(λ)는 압력 강하를 계산하는 핵심 매개 변수이지만, 그 값을 결정하려면 흐름 조건을 고려해야 합니다:
| 흐름 체제 | 레이놀즈 수(Re) | 마찰 계수 결정 |
|---|---|---|
| 층류 흐름 | Re < 2000 | λ = 64/Re |
| 전환 흐름 | 2000 < Re < 4000 | 신뢰할 수 없음 - 이 범위에서 설계하지 마십시오. |
| 난류 흐름 | Re > 4000 | 상대 거칠기(ε/D) 기반 조회 테이블 사용 |
실제 마찰 계수 조회 테이블
공압 시스템의 난류 흐름의 경우 이 단순화된 표를 사용하세요:
| 파이프 재질 | 상대 거칠기(ε/D) | 일반 레이놀즈 수에서의 마찰 계수(λ) |
|---|---|---|
| Re = 10,000 | ||
| 부드러운 튜브(PVC, 폴리우레탄) | 0.0001 – 0.0005 | 0.031 |
| 알루미늄 튜브 | 0.001 – 0.002 | 0.035 |
| 아연 도금 강철 | 0.003 – 0.005 | 0.042 |
| 녹슨 강철 | 0.01 – 0.05 | 0.054 |
실제 공압 시스템에서 압력 강하 계산하기
실제 사례를 살펴보겠습니다:
| 매개변수 | 가치/계산 | 예 |
|---|---|---|
| 파이프 직경(D) | 내경 | 8mm(0.008m) |
| 파이프 길이(L) | 총 직선 길이 | 5m |
| 유량(Q) | 시스템 요구 사항에서 | 20 표준 리터/초 |
| 공기 밀도(ρ) | 작동 압력에서 | 6bar에서 7.2kg/m³ |
| 유속(v) | v = Q/(π×D²/4) | v = 0.02m³/s/(π×0.008²/4) = 398m/s |
| 레이놀즈 수(Re) | Re = ρvD/μ | Re = 7.2×398×0.008/1.8×10-⁵ = 1,273,600 |
| 상대적 거칠기 | 폴리우레탄 튜브의 경우 | 0.0003 |
| 마찰 계수(λ) | 조회 테이블에서 | 0.017 |
| 압력 강하(ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0.017×(5/0.008)×(7.2×398²/2) = 6.07bar |
실제 적용 사례: 실린더 속도 문제 해결
작년에 저는 위스콘신에 있는 포장 장비 회사의 제조 엔지니어인 Sarah와 함께 일한 적이 있습니다. 그녀의 로드리스 실린더 시스템은 정확한 크기의 실린더와 적절한 공급 압력을 갖추고 있음에도 불구하고 예상 속도의 60%로만 작동하고 있었습니다.
시스템을 분석한 결과, 고유량 애플리케이션에 6mm 튜브를 사용하고 있다는 사실을 발견했습니다. 마찰 손실로 인해 2.1bar의 압력 강하가 발생하여 사용 가능한 힘과 속도가 크게 감소했습니다. 10mm 튜빙으로 업그레이드하여 압력 강하를 0.4bar로 줄였고, 그녀의 시스템은 다른 변경 없이 즉시 필요한 성능을 달성했습니다.
실제 시스템에서 마찰 손실에 영향을 미치는 요인
실제 마찰 손실에 영향을 미치는 요인은 여러 가지가 있습니다:
- 공기 온도: 온도가 높을수록 점도와 마찰이 증가합니다.
- 오염: 먼지와 기름은 효과적인 거칠기를 증가시킬 수 있습니다.
- 튜브 굽힘: 구부러진 튜브의 미세 변형으로 저항 증가
- 노화 악화: 시간이 지남에 따라 부식과 침전물이 거칠기를 증가시킵니다.
- 작동 압력: 압력이 높을수록 밀도 및 손실 증가
등가 길이 방식이 정확한 시스템 설계에 중요한 이유는 무엇인가요?
피팅, 밸브 및 굴곡부에서의 국부적 손실은 종종 직선 파이프의 마찰 손실을 초과하지만 많은 엔지니어가 이를 무시하거나 성능 문제를 초래하는 조잡한 추정 방법을 사용합니다.
등가 길이 방법은 피팅과 밸브의 국부적 손실을 동일한 압력 강하를 유발하는 직선 파이프의 등가 길이로 변환합니다. 이는 Le = K(D/λ)를 사용하여 계산되며, 여기서 Le는 등가 길이, K는 로컬 손실 계수4여기서 D는 파이프 직경, λ는 마찰 계수입니다. 이 방법은 계산을 간소화하고 보다 정확한 시스템 성능 예측을 제공합니다.
이 방법을 공압 시스템 설계에 효과적으로 적용하는 방법을 알아보세요.
일반적인 공압 부품의 등가 길이 표
다음은 일반적인 공압 구성 요소에 대한 실용적인 참조 표입니다:
| 구성 요소 | K-가치 | 등가 길이(Le/D) |
|---|---|---|
| 90° 팔꿈치(날카로운) | 0.9 | 30 |
| 90° 팔꿈치(표준 반경) | 0.3 | 10 |
| 45° 팔꿈치 | 0.2 | 7 |
| T-정션(흐름 통과) | 0.3 | 10 |
| T-정션(분기 흐름) | 1.0 | 33 |
| 볼 밸브(완전 개방) | 0.1 | 3 |
| 게이트 밸브(완전 개방) | 0.2 | 7 |
| 퀵 커넥트 커플링 | 0.4-0.8 | 13-27 |
| 체크 밸브 | 1.5-2.5 | 50-83 |
| 표준 유량 제어 밸브 | 1.0-3.0 | 33-100 |
등가 길이 방법 적용
이 방법을 효과적으로 사용하려면 다음과 같이 하세요:
- 공압 회로의 모든 구성 요소 식별
- 각 구성 요소의 K-값 또는 등가 길이 비율(Le/D)을 구합니다.
- 파이프 지름을 곱하여 등가 길이를 계산합니다.
- 실제 직선 파이프 길이에 모든 등가 길이를 더합니다.
- 마찰 손실 계산에 총 유효 길이를 사용합니다.
예를 들어, 5m의 직선 8mm 튜브와 4개의 90° 엘보, 1개의 T-정션, 2개의 퀵 커넥트로 구성된 시스템입니다:
| 구성 요소 | 수량 | Le/D | 등가 길이 |
|---|---|---|---|
| 90° 팔꿈치 | 4 | 10 | 4 × 10 × 0.008m = 0.32m |
| T-정션 | 1 | 10 | 1 × 10 × 0.008m = 0.08m |
| 빠른 연결 | 2 | 20 | 2 × 20 × 0.008m = 0.32m |
| 총 등가 길이 | 0.72m | ||
| 실제 직선 길이 | 5.00m | ||
| 총 유효 길이 | 5.72m |
즉, 5m 시스템은 로컬 손실로 인해 실제로는 5.72m 시스템처럼 작동하며, 유효 길이가 14.4% 증가합니다.
사례 연구: 조립 시스템에서 밸브 배치 최적화
저는 최근 애리조나에 있는 전자제품 조립 공장의 자동화 엔지니어인 미구엘을 도왔습니다. 그의 픽 앤 플레이스 시스템은 고품질 부품을 사용했음에도 불구하고 동작과 사이클 시간이 일정하지 않았습니다.
분석 결과, 그의 밸브 매니폴드는 실린더에서 3m 떨어진 곳에 위치해 있었고 회로에는 수많은 피팅이 포함되어 있었습니다. 등가 길이 계산 결과 3m의 실제 거리는 국부적 손실로 인해 7.2m의 유효 길이를 가졌으며, 이는 직선 파이프 거리의 두 배가 넘는 길이였습니다!
밸브 매니폴드를 실린더에 더 가깝게 재배치하고 여러 피팅을 제거하여 유효 길이를 7.2m에서 2.1m로 줄였습니다. 그 결과 압력 강하가 70% 감소하여 동작이 일관되고 사이클 시간이 15% 단축되었습니다.
로컬 손실 최소화를 위한 실용적인 팁
공압 시스템의 로컬 손실을 줄이려면:
- 스윕 또는 둥근 팔꿈치 사용 날카로운 굴곡 대신 (K-값 67% 감소)
- 피팅 수 최소화 보다 직접적인 경로를 계획하여
- 제한이 적은 구성 요소 선택 적절한 경우 풀보어 볼 밸브와 같은
- 적절한 피팅 사이즈 맞추기 - 크기가 작은 피팅은 불균형적인 손실을 초래합니다.
- 액추에이터에 가까운 곳에 밸브 배치 유효 튜브 길이를 최소화하기 위해
축소된 보어 섹션을 통해 공기가 흐르면 어떻게 될까요?
부분적으로 닫힌 밸브, 크기가 작은 피팅 또는 직경 전환과 같이 공압 회로에서 보어 섹션이 줄어들면 시스템 성능에 심각한 영향을 미칠 수 있는 심각한 유량 제한이 발생합니다.
축소된 보어 섹션을 통해 공기가 흐르는 경우, 압력 강하5 는 ΔP = ρ(v₂² - v₁²)/2 공식에 따라 발생하며, 여기서 v₁는 제한 전 속도, v₂는 제한 후 속도입니다. 이는 보어 비율 보정 계수 C = (1 - (d/D)⁴)를 사용하여 보정할 수 있으며, 여기서 d는 축소된 직경이고 D는 원래 직경입니다. 이 계수는 실제 시스템 성능을 예측하고 구성 요소의 크기 부족을 방지하는 데 도움이 됩니다.
보어 섹션 감소의 실질적인 의미와 시스템 설계에서 이를 고려하는 방법을 살펴보겠습니다.
직경 전환 시 압력 강하 계산하기
공기가 큰 직경에서 작은 직경으로 흐르면 다음을 사용하여 압력 강하를 계산할 수 있습니다:
| 매개변수 | 공식 | 예 |
|---|---|---|
| 원래 지름(D) | 사양에서 | 10mm |
| 감소된 직경(d) | 사양에서 | 6mm |
| 보어 비율(d/D) | 단순 나누기 | 0.6 |
| 유량(Q) | 시스템 요구 사항에서 | 15 표준 리터/초 |
| 원래 파이프의 속도(v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| 감소 구간에서의 속도(v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| 압력 강하(ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0.88 바 |
| 보상 계수(C) | C = (1 - (d/D)⁴) | 0.87 |
일반적인 보어 감소 시나리오와 그 영향
다양한 보어 감소가 유량에 미치는 영향은 다음과 같습니다:
| 보어 감소 | 유량 감소 | 압력 강하 증가 |
|---|---|---|
| 10mm ~ 8mm | 36% | 2.4× |
| 10mm ~ 6mm | 64% | 7.7× |
| 10mm ~ 4mm | 84% | 39× |
| 8mm ~ 6mm | 44% | 3.2× |
| 8mm ~ 4mm | 75% | 16× |
| 6mm ~ 4mm | 56% | 5.1× |
이 수치는 직경의 사소한 감소가 시스템 성능에 극적인 영향을 미칠 수 있는 이유를 잘 보여줍니다.
여러 제한의 누적 효과
실제 공압 회로에서는 여러 제한이 직렬로 발생합니다. 그 효과는 누적되며 다음을 사용하여 계산할 수 있습니다:
- 각 제한 사항을 해당 C-팩터로 변환하기
- 총 C 계수를 계산합니다: C총계 = 1 - (1-C₁)(1-C₂)(1-C₃)...
- 이 총계수를 사용하여 전체 시스템 성능 감소를 결정합니다.
사례 연구: 밸브-액추에이터 불일치 문제 해결하기
지난달 저는 노스캐롤라이나에 있는 한 가구 제조 공장의 유지보수 감독관인 Thomas와 함께 일했습니다. 그의 새로운 로드리스 실린더 시스템은 제조업체에서 권장하는 밸브 크기를 사용했음에도 불구하고 예상 속도의 절반 이하로 작동하고 있었습니다.
조사 결과 그의 회로에 여러 개의 구멍이 있는 것으로 밝혀졌습니다:
- 8mm 밸브 포트에 10mm 공급 라인(C₁ = 0.36)
- 8mm 밸브 포트 - 6mm 피팅(C₂ = 0.44)
- 내부 제한이 있는 6mm 피팅 - 8mm 실린더 포트(C₃ = 0.32)
총 보상 계수는 Ctotal = 1 - (1-0.36)(1-0.44)(1-0.32) = 0.75로, 그의 시스템이 이론적 유량 용량 중 75%를 잃고 있다는 뜻입니다!
시스템 전체에 걸쳐 적절한 크기의 부품으로 업그레이드함으로써 이러한 제한을 없애고 실린더나 공급 압력을 변경하지 않고도 필요한 성능을 달성했습니다.
보어 감소 손실을 최소화하기 위한 실용적인 전략
보어 감소로 인한 손실을 줄입니다:
- 일관된 크기 구성 요소 공압 회로 전체에 걸쳐
- 실용적인 가장 큰 튜브 크기 사용 고유량 애플리케이션용
- 내부 구성 요소 제한에 주의하세요연결 크기뿐만 아니라
- 병렬 흐름 경로 고려 높은 유량 요구 사항의 경우
- 불필요한 어댑터 및 전환 제거 가능한 경우
공압 시스템의 '가장 약한 연결 고리' 원리
공압 시스템의 성능은 가장 제한적인 구성 요소에 의해 제한된다는 점을 기억하세요. 크기가 작은 부품 하나가 시스템의 다른 곳에 있는 적절한 크기의 부품의 이점을 무효화할 수 있습니다.
예를 들어, 10mm 튜브, 10mm 밸브가 있지만 실린더에 6mm 피팅이 있는 시스템은 전체적으로 6mm 부품이 있는 시스템과 본질적으로 동일한 성능을 발휘하지만 비용은 더 높습니다.
결론
실제 조건에서 예상대로 작동하는 공압 시스템을 설계하려면 마찰 계수 표, 등가 길이 방법, 보어 감소 보정 등을 통해 유량 저항을 이해하고 올바르게 계산하는 것이 필수적입니다. 이러한 계산 방법과 설계 원칙을 적용하면 로드리스 실린더 애플리케이션 및 기타 공압 시스템을 최적화하여 성능과 안정성을 극대화할 수 있습니다.
공압 시스템의 유량 저항에 대한 FAQ
공압 시스템에서 허용되는 압력 강하는 어느 정도인가요?
허용되는 압력 강하는 애플리케이션 요구 사항에 따라 다르지만, 효율적인 작동을 위해 총 압력 강하를 공급 압력의 10-15%로 제한하는 것이 일반적인 지침입니다. 6bar 시스템의 경우, 이는 총 압력 강하를 0.6~0.9bar 미만으로 유지해야 함을 의미합니다. 중요한 애플리케이션의 경우 일관된 성능을 유지하기 위해 5-8%의 더 낮은 압력 강하가 필요할 수 있습니다.
튜브 직경과 압력 강하 사이에는 어떤 관계가 있나요?
공압 시스템의 난류 흐름에서 압력 강하는 직경의 5제곱(D⁵)에 반비례합니다. 즉, 튜브 직경을 두 배로 늘리면 압력 강하가 약 32배 감소합니다. 예를 들어, 6mm에서 12mm 튜브를 늘리면 동일한 유량 조건에서 압력 강하가 1.5bar에서 0.047bar로 감소할 수 있습니다.
공압 애플리케이션에 적합한 튜브 크기는 어떻게 결정하나요?
유량 요구 사항과 허용 가능한 압력 강하에 따라 튜브 크기를 선택합니다. 레이놀즈 수와 마찰 계수를 계산한 다음 Darcy-Weisbach 방정식을 사용하여 다양한 직경에 대한 압력 강하를 결정합니다. 공간 제약과 비용을 고려하면서 압력 강하를 허용 가능한 한도(일반적으로 공급 압력 10% 미만) 이내로 유지하는 가장 작은 직경을 선택합니다.
90° 엘보 또는 5미터의 직선 튜브 중 무엇이 더 많은 제한을 만들까요?
날카로운 90° 엘보우는 일반적으로 파이프 직경 30개의 직선 튜빙에 해당하는 저항을 생성합니다. 8mm 튜브의 경우, 날카로운 엘보 1개는 약 240mm(30 × 8mm)의 직선 튜브에 해당합니다. 즉, 5m의 직선 튜빙은 단일 엘보보다 약 21배 더 많은 제한을 생성합니다. 그러나 시스템에는 여러 개의 엘보와 피팅이 포함되는 경우가 많으며, 누적 효과는 직선 길이 손실을 초과할 수 있습니다.
빠른 연결 피팅은 시스템 성능에 어떤 영향을 미치나요?
표준 퀵 커넥트 피팅은 일반적으로 직선 튜브의 파이프 직경 15~25개에 해당하는 국부적 손실을 발생시킵니다. 더 중요한 것은 많은 퀵 커넥트의 내부 제한이 공칭 크기보다 작다는 점입니다. "10mm" 퀵 커넥트의 경우 내부 제한이 7-8mm에 불과할 수 있으며, 이 경우 보어 감소로 인해 유량이 50-70%까지 감소할 수 있습니다.
부분적으로 닫힌 유량 제어 밸브가 시스템 성능에 미치는 영향은 무엇인가요?
유량 제어 밸브가 전체 보어 면적의 50%로 닫히면 직경과 유량 사이의 비선형 관계로 인해 유량이 50%만 감소하는 것이 아니라 약 75%가 감소합니다. 압력 강하는 속도 변화의 제곱에 따라 증가하므로 동일한 유량 조건에서 유효 직경을 절반으로 줄이면 압력 강하가 약 16배 증가합니다.
-
파이프의 마찰로 인한 압력 손실을 계산하기 위해 유체 역학에서 기본적이고 널리 사용되는 공식인 Darcy-Weisbach 방정식에 대한 자세한 분석을 제공합니다. ↩
-
다양한 유체 흐름 상황에서 흐름 패턴(층류 또는 난류)을 예측하는 데 사용되는 중요한 무차원 수량인 레이놀즈 수에 대한 명확한 정의를 제공합니다. ↩
-
엔지니어가 파이프의 압력 강하를 결정하는 표준 도구인 레이놀즈 수와 상대 거칠기에 대한 다아시 마찰 계수를 표시하는 종합 그래프인 무디 다이어그램을 제공합니다. ↩
-
등가 길이 방법의 일부로 파이프 피팅 또는 밸브의 압력 손실을 특성화하는 데 사용되는 무차원 수치인 K-값 또는 국부 손실 계수의 개념에 대해 설명합니다. ↩
-
연속성 방정식과 베르누이의 원리를 바탕으로 유체가 제한 장치(오리피스)를 통과할 때 발생하는 압력 강하에 대한 물리학을 자세히 설명합니다. ↩



