Kaip vibracijos rezonansas veikia pramoninės įrangos našumą?

Kiekvieno techninės priežiūros inžinieriaus košmaras - netikėtas įrangos gedimas. Kai mašinos vibruoja savo natūraliu dažniu, katastrofiška žala gali atsirasti per kelias minutes. Esu matęs, kaip ši problema įmonėms kainuoja tūkstančius prastovų.

Vibracijos rezonansas¹ atsiranda, kai išorinė jėga sutampa su sistemos savituoju dažniu ir sukelia sustiprintus virpesius, kurie gali sugadinti įrangą. Norint išvengti gedimų ir prailginti mašinų tarnavimo laiką, labai svarbu suprasti ir kontroliuoti šį reiškinį.

Leiskite pasidalyti trumpa istorija. Praėjusiais metais man paskambino klientas iš Vokietijos ir puolė į paniką. Jų gamybos linija sustojo, nes cilindras be lazdelių smarkiai vibravo. Problema? Rezonansas. Šio straipsnio pabaigoje suprasite, kaip nustatyti panašias problemas savo sistemose ir užkirsti joms kelią.

Turinys

Natūralaus dažnio formulė: Kaip apskaičiuoti pažeidžiamus sistemos taškus?
"Mass-Spring" modelis: Kodėl šis supaprastintas požiūris toks vertingas?
slopinimo koeficiento optimizavimas: Kokie eksperimentai duoda geriausius rezultatus?
Išvada
DUK apie vibracinį rezonansą

Natūralaus dažnio formulė: Kaip apskaičiuoti pažeidžiamus sistemos taškus?

Pirmas žingsnis siekiant išvengti rezonanso problemų - suprasti savo įrangos natūralųjį dažnį. Ši kritinė vertė nustato, kada jūsų sistema yra labiausiai pažeidžiama dėl vibracijos problemų.

Svetainė savasis dažnis² (fn) galima apskaičiuoti pagal formulę: fn = (1/2π) × √(k/m), kur k - standumo koeficientas, o m - masė. Šis skaičiavimas parodo, kokiu dažniu jūsų sistema rezonuos, jei ją sužadins atitinkamos išorinės jėgos.

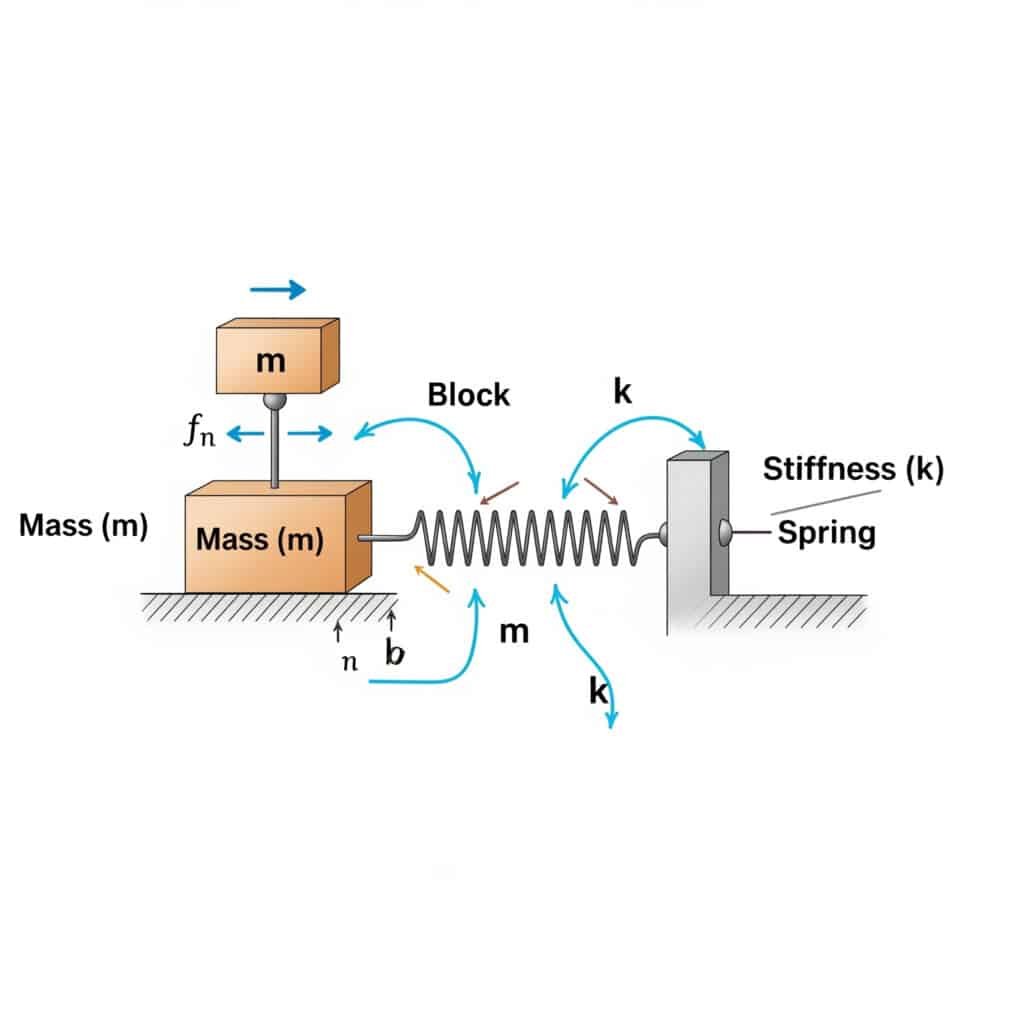
Švari, mokomoji diagrama, paaiškinanti savitąjį dažnį. Iliustracijoje pavaizduota paprasta masės ir spyruoklės sistema, kurioje blokas pažymėtas "Masė (m)", o spyruoklė - "Standumas (k)". Judėjimo linijos rodo, kad sistema svyruoja. Šalia diagramos aiškiai pavaizduota formulė "fn = (1/2π) × √(k/m)", o rodyklės aiškiai susieja lygties kintamuosius "m" ir "k" su atitinkamomis fizikinėmis dalimis. — savasis dažnis

Apsilankęs Šveicarijoje esančioje gamykloje pastebėjau, kad jų pneumatiniai cilindrai be lazdelių sugenda anksčiau laiko. Jų techninės priežiūros komanda nebuvo apskaičiavusi jų sąrankos savojo dažnio. Pritaikę šią formulę nustatėme, kad jų darbinis greitis buvo pavojingai artimas sistemos savitajam dažniui.

Praktinis natūraliojo dažnio skaičiavimų taikymas

Natūraliojo dažnio formulė nėra tik teorinė - ji tiesiogiai taikoma įvairiose pramonės srityse:

Įrangos pasirinkimas: Komponentų, kurių savieji dažniai toli nuo jūsų darbo sąlygų, pasirinkimas
Prevencinė priežiūra: Patikrinimų planavimas pagal vibracijos rizikos profilius
Trikčių šalinimas: Pagrindinės netikėtos vibracijos priežasties nustatymas

Bendrosios pramoninių komponentų natūraliojo dažnio vertės

Komponentas	Tipinis natūraliojo dažnio diapazonas (Hz)
Cilindrai be strypų	10-50 Hz
Montavimo laikikliai	20-100 Hz
Pagalbinės struktūros	5-30 Hz
Valdymo vožtuvai	40-200 Hz

Kritiniai veiksniai, turintys įtakos natūraliajam dažniui

Atrodo, kad apskaičiuoti savitąjį dažnį yra paprasta, tačiau realiame pasaulyje gali būti sudėtinga dėl keleto veiksnių:

Nevienodas masės pasiskirstymas: Daugumos pramoninių komponentų masė nėra tobulai pasiskirsčiusi
Kintamas standumas: Komponentų standumas skirtingomis kryptimis gali skirtis.
Prijungimo taškai: Komponentų montavimo būdas daro didelę įtaką jų vibracijos savybėms
Temperatūros poveikis: Tiek masės, tiek standumo savybės gali kisti priklausomai nuo temperatūros

"Mass-Spring" modelis: Kodėl šis supaprastintas požiūris toks vertingas?

Masės ir spyruoklės modelis suteikia intuityvią sistemą sudėtingoms vibracijos sistemoms suprasti. Sudėtingas mašinas jis sumažina iki pagrindinių elementų, kuriuos inžinieriai gali lengvai analizuoti.

Svetainė masės ir spyruoklės modelis³ supaprastina vibracijų analizę, nes mechaninės sistemos vaizduojamos kaip diskrečios masės, sujungtos spyruoklėmis. Šis metodas leidžia inžinieriams prognozuoti sistemos elgseną, nustatyti galimas rezonanso problemas ir kurti veiksmingus sprendimus be sudėtingos matematikos.

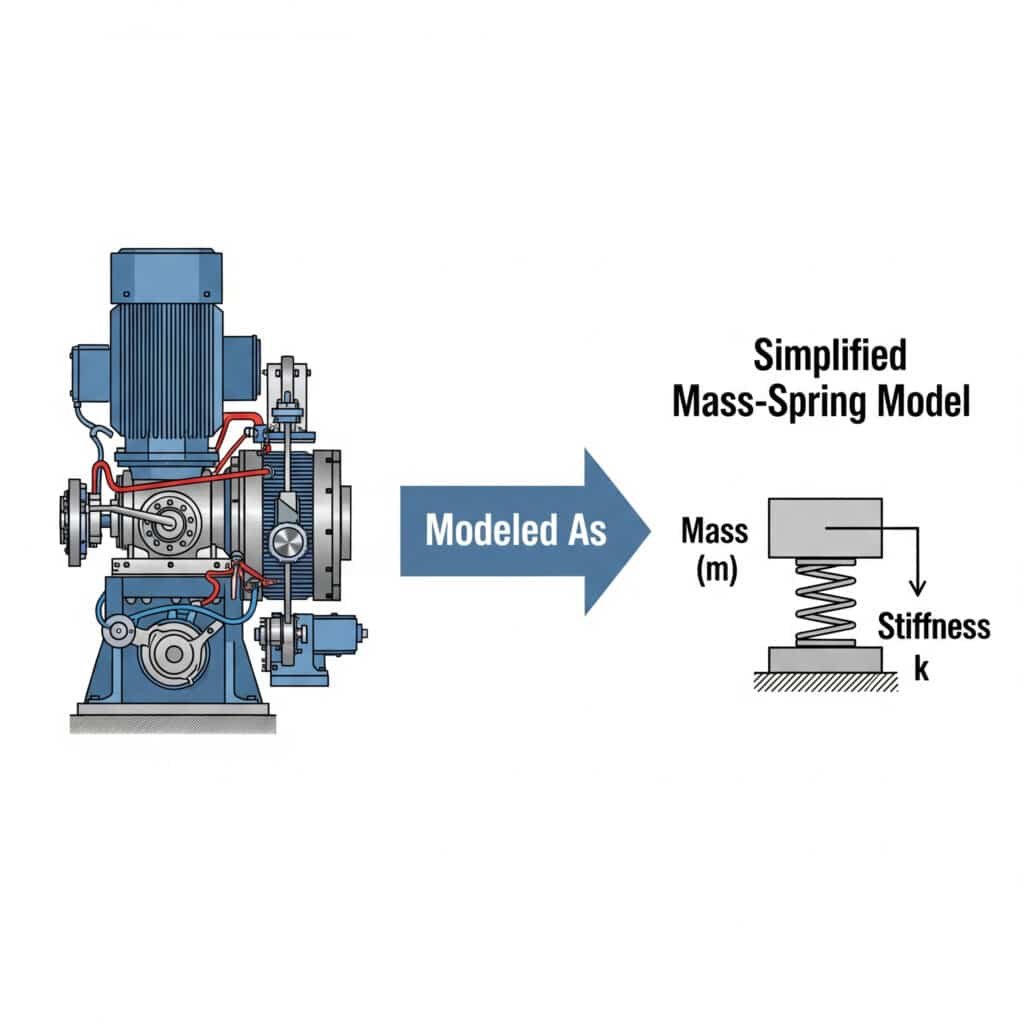
Lyginamasis infografikas, kuriame paaiškinamas masės ir spyruoklės modelis. Kairėje pusėje, po užrašu "Sudėtinga mechaninė sistema", pateikta išsami pramoninio variklio iliustracija. Didelė rodyklė su užrašu "Modeliuojama kaip" rodo į dešinę. Dešinėje pusėje, po užrašu "Supaprastintas masės ir spyruoklės modelis", visas sudėtingas variklis pavaizduotas paprastu bloku, pažymėtu "Masė (m)", sujungtu su paprasta spyruokle, pažymėta "Standumas (k)". — masės ir spyruoklės modelis

Prisimenu, kaip dirbau su automobilių dalių gamintoju Mičigane, kuris negalėjo suprasti, kodėl jų valdomi cilindrai be lazdelių sugenda. Sumodeliavę jų sistemą kaip paprastą masės ir spyruoklės sąrangą, nustatėme, kad tvirtinimo kronšteinai veikė kaip nenumatytos spyruoklės, sukeldami rezonansą.

Realių sistemų konvertavimas į masės ir spyruoklės modelius

Norėdami taikyti šį metodą savo įrangai:

Nustatykite pagrindines mases: Nustatykite, kurios sudedamosios dalys sudaro didelį svorį
Raskite spyruoklių elementus: Suraskite komponentus, kurie kaupia ir atiduoda energiją (tikras spyruokles, lanksčius laikiklius ir pan.)
Žemėlapio jungtys: Užfiksuokite, kaip sąveikauja masės ir spyruoklės
Supaprastinkite: Sujungti panašius elementus, kad sukurtumėte valdomą modelį

Masinių spyruoklių sistemų tipai

Sistemos tipas	Aprašymas	Bendros programos
Vienas DOF	Viena masė su viena spyruokle	Paprasti pneumatiniai cilindrai
Daugiafunkcinė sistema	Kelios masės su keliomis spyruoklėmis	Sudėtingos mašinos su daugybe komponentų
Nuolatinis	Begalinis DOF (reikia kitokios analizės)	Sijos, plokštės ir korpusai

Išplėstinio modeliavimo aspektai

Nors pagrindinis masės ir spyruoklės modelis yra vertingas, keletas patobulinimų daro jį realistiškesnį:

Amortizatorių pridėjimas: Realiose sistemose visada vyksta energijos sklaida
Atsižvelgiant į netiesiškumą: Spyruoklės ne visada seka Hūko dėsnis⁴ puikiai
Priverstinės vibracijos apskaita: Išorinės jėgos keičia sistemos elgseną
Įskaitant susiejimo poveikį: Judėjimas viena kryptimi gali turėti įtakos kitoms kryptims

slopinimo koeficiento optimizavimas: Kokie eksperimentai duoda geriausius rezultatus?

Amortizacija yra geriausia apsauga nuo rezonanso problemų. Eksperimentuodami raskite optimalų slopinimo santykį, kuris gali gerokai pagerinti sistemos veikimą ir patikimumą.

Amortizavimo koeficientas⁵ optimizavimo eksperimentai apima sistemingą įvairių slopinimo konfigūracijų bandymą, siekiant rasti idealią pusiausvyrą tarp vibracijos kontrolės ir sistemos reakcijos. Optimalus slopinimo koeficientas paprastai būna nuo 0,2 iki 0,7 ir užtikrina pakankamą vibracijos slopinimą be pernelyg didelių energijos nuostolių.

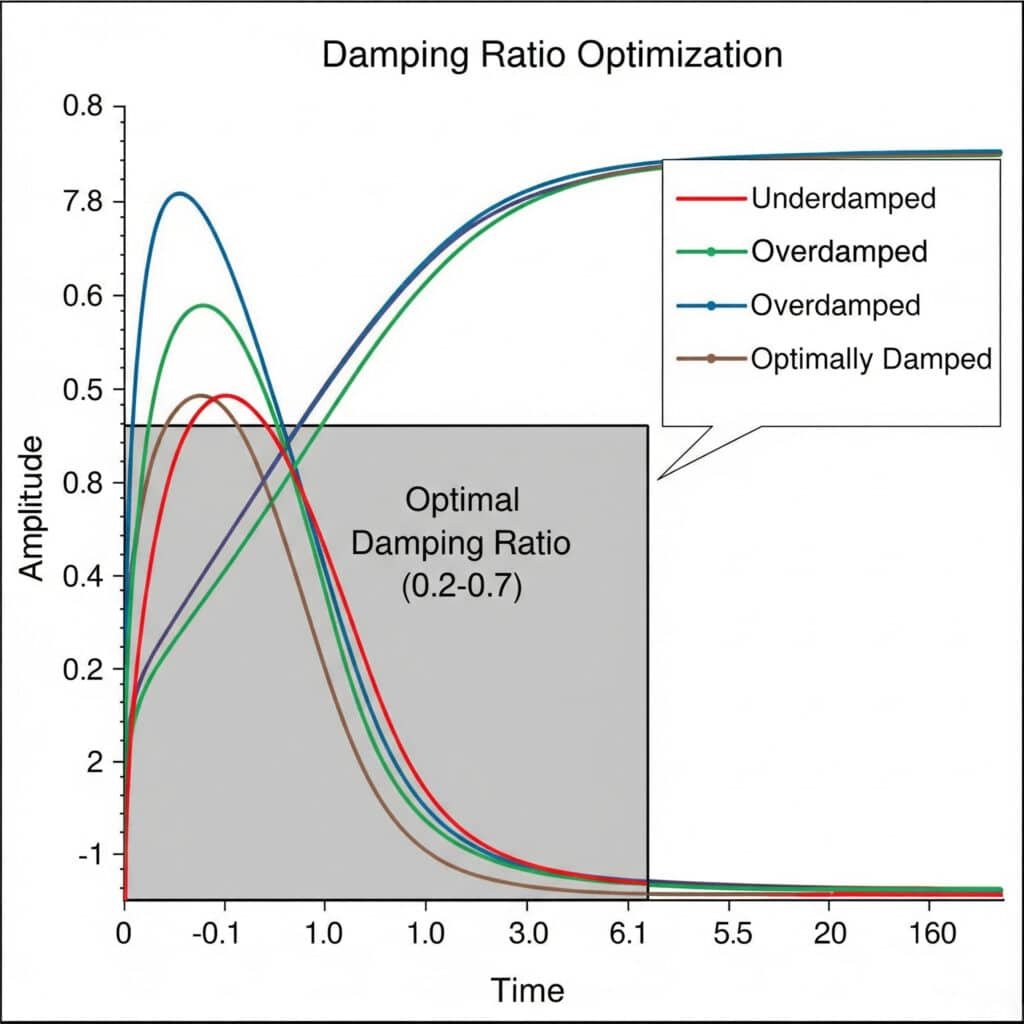
Diagrama, iliustruojanti slopinimo santykio optimizavimą, nubraižant sistemos "Amplitudės" ir "Laiko" santykį. Jame pateikiamos trys skirtingos atsako kreivės: "nepakankamai amortizuota" kreivė, kuri smarkiai svyruoja, "per daug amortizuota" kreivė, kuri labai lėtai grįžta į nulį be svyravimų, ir "optimaliai amortizuota" kreivė, kuri greitai nusistovi su minimaliu viršijimu. Ši ideali reakcija pažymėta šešėliu ir pažymėta "Optimalus slopinimo koeficientas (0,2-0,7)". — slopinimo koeficiento optimizavimas

Praėjusį mėnesį padėjau maisto perdirbimo įrangos gamintojui Prancūzijoje išspręsti nuolatines vibracijos problemas, susijusias su jų magnetiniais cilindrais be lazdelių. Atlikę keletą slopinimo koeficiento eksperimentų, nustatėme, kad jų pirminės konstrukcijos slopinimo koeficientas buvo tik 0,05 - per mažas, kad būtų išvengta rezonanso problemų.

Eksperimentinė slopinimo koeficiento bandymo sąranka

Atlikti efektyvaus slopinimo optimizavimo eksperimentus:

Bazinis matavimas: Įrašykite sistemos atsaką be papildomo slopinimo
Inkrementinis testavimas: Kontroliuojamais žingsniais pridėkite slopinimo elementų
Reakcijos matavimas: Matuokite amplitudę, nusistovėjimo laiką ir dažninę charakteristiką
Duomenų analizė: Apskaičiuokite kiekvienos konfigūracijos slopinimo koeficientą
Patvirtinimas: Patikrinkite veikimą faktinėmis darbo sąlygomis

Duslinimo technologijų palyginimas

Amortizavimo technologija	Privalumai	Apribojimai	Tipinės programos
Klampos slopintuvai	Numatomas veikimas, stabili temperatūra	Reikalinga techninė priežiūra, galimi nutekėjimai	Sunkioji technika, tikslioji įranga
Trinties slopintuvai	Paprastas dizainas, ekonomiškas	Dėvėjimasis laikui bėgant, netiesinė elgsena	Konstrukcinės atramos, pagrindinės mašinos
Medžiagos slopinimas	Nėra judančių dalių, kompaktiškas	Ribotas reguliavimo diapazonas	Tikslieji prietaisai, vibracijos izoliacija
Aktyvus slopinimas	Prisitaikymas prie kintančių sąlygų	Sudėtinga, reikalinga galia	Kritiniai taikymai, kintamo greičio įranga

Amortizavimo optimizavimas skirtingoms darbo sąlygoms

Idealus slopinimo santykis nėra universalus - jis priklauso nuo konkretaus naudojimo būdo:

Didelės spartos operacijos: Mažesni slopinimo koeficientai (0,1-0,3) išlaiko reakciją
Tikslūs taikymai: Didesni slopinimo koeficientai (0,5-0,7) užtikrina stabilumą
Kintamos apkrovos sistemos: Gali prireikti adaptyvaus slopinimo
Temperatūrai jautri aplinka: Apsvarstykite stabilių savybių slopinimo medžiagas

Atvejo analizė: Cilindrų be strypų amortizacijos optimizavimas

Optimizuodami pakavimo mašinai skirtą dvigubo veikimo cilindrą be strypų, išbandėme penkias skirtingas slopinimo konfigūracijas:

Standartinės galinės pagalvėlės: slopinimo koeficientas = 0,12
Prailgintos pagalvėlės: slopinimo koeficientas = 0,25
Išoriniai amortizatoriai: slopinimo koeficientas = 0,41
Kompozitiniai montavimo laikikliai: slopinimo koeficientas = 0,38
Kombinuotas metodas (3+4): slopinimo koeficientas = 0,53

Kombinuotas metodas buvo geriausias, nes vibracijos amplitudė buvo sumažinta 78%, išlaikant priimtiną atsako laiką.

Išvada

Norint išvengti įrangos gedimų, labai svarbu suprasti vibracijos rezonansą apskaičiuojant savitąjį dažnį, modeliuojant mases ir spyruokles bei optimizuojant slopinimo koeficientą. Taikydami šiuos principus, galite pailginti mašinų eksploatavimo laiką, sutrumpinti prastovas ir pagerinti bendrą sistemos veikimą.

DUK apie vibracinį rezonansą

Kas yra pramoninės įrangos vibracinis rezonansas?

Vibracinis rezonansas atsiranda tada, kai išorinė jėga sutampa su sistemos savituoju dažniu ir sukelia sustiprintus virpesius. Pramonės įrangoje šis reiškinys gali sukelti pernelyg didelį judėjimą, komponentų nuovargį ir katastrofiškus gedimus, jei nėra tinkamai valdomas.

Kaip nustatyti, ar mano sistema rezonuoja?

Ieškokite tokių simptomų, kaip nepaaiškinamas triukšmo padidėjimas, matoma vibracija esant tam tikram greičiui, ankstyvi komponentų gedimai ir eksploatacinių savybių pablogėjimas, atsirandantis esant vienodiems veikimo taškams. Vibracijos analizės įrankiai gali patvirtinti rezonanso sąlygas.

Koks skirtumas tarp priverstinės vibracijos ir rezonanso?

Priverstinė vibracija atsiranda, kai sistemą veikia išorinė jėga, o rezonansas - tai specifinė būklė, kai priverstinis dažnis sutampa su sistemos savituoju dažniu ir dėl to sustiprėja atsakas. Visi rezonansai yra susiję su priverstiniais virpesiais, tačiau ne visi priverstiniai virpesiai sukelia rezonansą.

Kaip bepakopio pneumatinio cilindro konstrukcija veikia jo vibracijos charakteristikas?

Bepakopių pneumatinių cilindrų su judančiu vežimėliu, vidine sandarinimo sistema ir kreipiamaisiais mechanizmais konstrukcija kelia unikalių vibracijos iššūkių. Prailgintas profilis veikia kaip sija, kuri gali lankstytis, vežimėlio masė sukuria inercines jėgas, o sandarinimo juostos gali sukelti kintamą trintį.

Kokiais paprastais pakeitimais galima sumažinti esamos įrangos rezonansą?

Jei esama įranga patiria rezonanso problemų, apsvarstykite galimybę pridėti masės, kad pasikeistų savasis dažnis, sumontuoti išorinius slopintuvus ar amortizatorius, pakeisti montavimo metodus, kad būtų užtikrinta vibracijos izoliacija, arba sureguliuoti darbo greitį, kad būtų išvengta rezonansinių dažnių.

Pateikiamas esminis mechaninio rezonanso paaiškinimas, dažnai su vaizdiniais pavyzdžiais, parodantis, kaip maža periodinė jėga gali sukelti didelės amplitudės sistemos svyravimus. ↩
Išsamiai nagrinėjama fizikinė savojo dažnio, t. y. konkretaus dažnio, kuriuo sistema linkusi svyruoti, jei nėra jokios varomosios ar slopinamosios jėgos, samprata. ↩
Paaiškina masės ir spyruoklės modelio, kuris yra pagrindinis fizikos ir inžinerijos idealizavimo būdas, naudojamas sudėtingoms sistemoms, kurioms būdingas paprastas harmoninis judėjimas, analizuoti, principus. ↩
Išsami informacija apie Hūko dėsnį - fizikos principą, kuris teigia, kad jėga, reikalinga spyruoklei ištempti arba suspausti tam tikru atstumu, yra tiesiogiai proporcinga tam atstumui. ↩
Apibūdina slopinimo koeficientą - nedimensinį matą, kuris apibrėžia, kaip sistemos svyravimai po trikdžių slopsta, o tai labai svarbu siekiant kontroliuoti rezonansą. ↩

Sveiki, esu Chuckas, vyresnysis ekspertas, turintis 15 metų patirtį pneumatikos pramonėje. Bendrovėje "Bepto Pneumatic" daugiausia dėmesio skiriu aukštos kokybės, mūsų klientams pritaikytų pneumatinių sprendimų teikimui. Mano kompetencija apima pramonės automatizavimą, pneumatinių sistemų projektavimą ir integravimą, taip pat pagrindinių komponentų taikymą ir optimizavimą. Jei turite klausimų arba norėtumėte aptarti savo projekto poreikius, nedvejodami kreipkitės į mane el. paštu chuck@bepto.com.