Vai jūsu pneimatiskajās sistēmās ir problēmas ar lēniem cilindru apgriezieniem, nekonsekventu kustību vai nepietiekamu spēku? Šīs bieži sastopamās problēmas bieži rodas no nepareizi saprasta vaininieka - plūsmas pretestības. Daudzi inženieri nosaka pneimatisko komponentu izmērus, pamatojoties tikai uz spiediena un spēka prasībām, neņemot vērā plūsmas pretestības kritisko ietekmi uz reālo darbību.
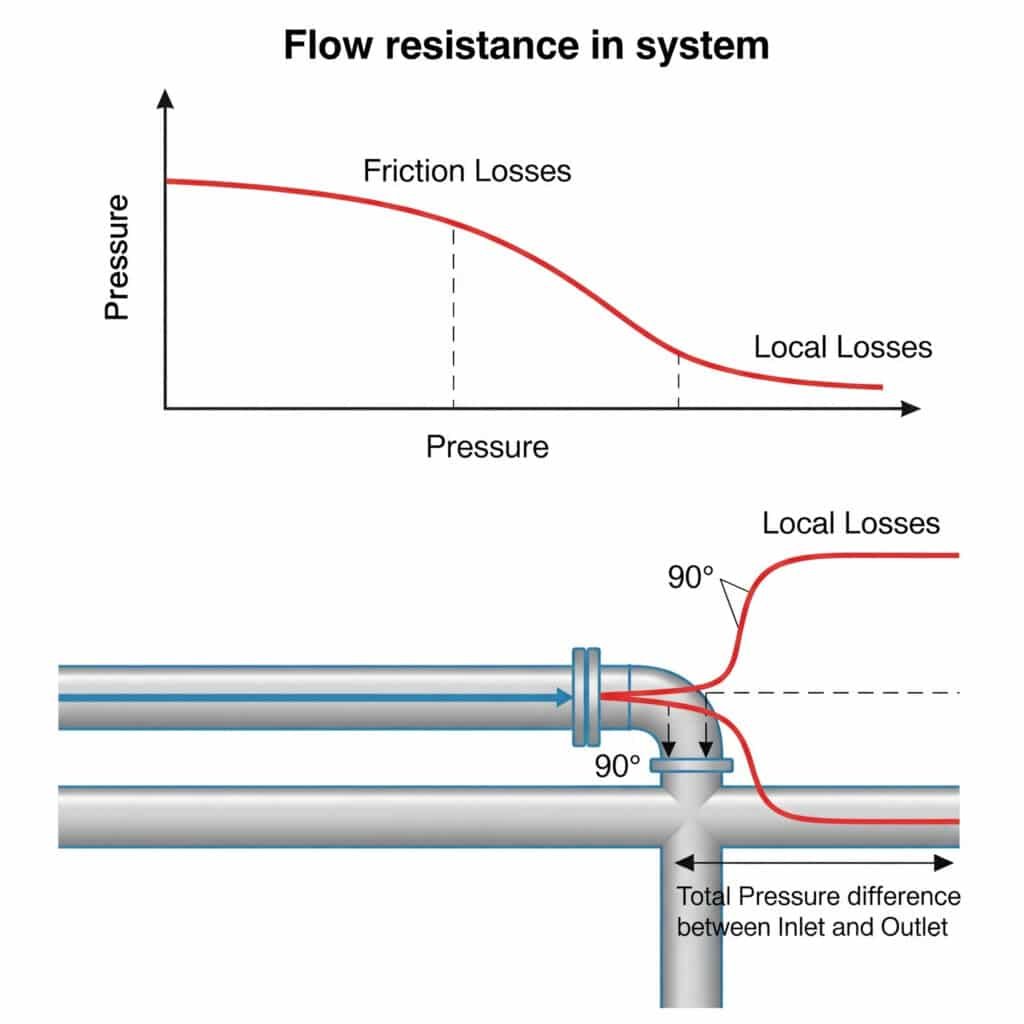
Plūsmas pretestība pneimatiskajās sistēmās rada spiediena kritumus, kas samazina pieejamo spēku, ierobežo maksimālo ātrumu un izraisa nekonsekventu kustību. Šo pretestību rada gan berze taisnās caurulēs (berzes zudumi), gan traucējumi pie savienotājelementiem, līkumiem un vārstiem (vietējie zudumi). Kopā šīs pretestības var samazināt faktisko sistēmas veiktspēju par 20-50% salīdzinājumā ar teorētiskajiem aprēķiniem.
Vairāk nekā 15 gadu laikā, kopš es strādāju Bepto ar pneimatiskajām sistēmām, esmu redzējis neskaitāmus gadījumus, kad plūsmas pretestības izpratne un novēršana ir pārveidojusi nepietiekami efektīvas sistēmas par uzticamām un efektīvām operācijām. Ļaujiet man dalīties ar to, ko esmu iemācījies par šo slēpto veiktspējas traucēkļu aprēķināšanu un samazināšanu līdz minimumam.
Satura rādītājs
- Kā faktiski aprēķināt berzes zudumus pneimatiskajās līnijās?
- Kāpēc ekvivalentā garuma metode ir kritiski svarīga precīzai sistēmas projektēšanai?
- Kas notiek, kad gaiss plūst caur samazinātām urbuma sekcijām?
- Secinājums
- Bieži uzdotie jautājumi par plūsmas pretestību pneimatiskajās sistēmās
Kā faktiski aprēķināt berzes zudumus pneimatiskajās līnijās?
Trīšanas zudumi taisnās caurulēs un caurulītēs ir plūsmas pretestības aprēķinu pamatā, taču daudzi inženieri paļaujas uz pārāk vienkāršotiem likumsakarībām, kas noved pie pārāk maza izmēra sistēmām.
Berzes zudumus pneimatiskajās līnijās aprēķina, izmantojot formulu Dārsija-Veisbaha vienādojums1: ΔP = λ(L/D)(ρv²/2), kur λ ir berzes koeficients, L ir caurules garums, D ir caurules diametrs, ρ ir gaisa blīvums un v ir plūsmas ātrums. Pneimatiskajās sistēmās berzes koeficients λ mainās atkarībā no Reinoldsa skaitlis2 un relatīvo raupjumu, un to parasti nosaka, izmantojot uzskates tabulas vai Moody diagramma3.
Izpratnei par berzes zudumiem ir praktiska nozīme sistēmu projektēšanā un problēmu novēršanā. Ļaujiet man to sadalīt praktiski izmantojamās atziņās.
Efektīva berzes koeficientu tabulu izmantošana
Berzes koeficients (λ) ir galvenais parametrs spiediena kritumu aprēķināšanā, bet, nosakot tā vērtību, jāņem vērā plūsmas apstākļi:
| Plūsmas režīms | Reinoldsa skaitlis (Re) | Berzes koeficienta noteikšana |
|---|---|---|
| Laminārā plūsma | Re < 2000 | λ = 64/Re |
| Pārejas plūsma | 2000 < Re < 4000 | Uzticams - izvairieties no projektēšanas šajā diapazonā |
| Turbulenta plūsma | Re > 4000 | Izmantojiet uzskates tabulas, pamatojoties uz relatīvo raupjumu (ε/D). |
Praktiskā berzes koeficienta uzrādīšanas tabula
Pneimatisko sistēmu turbulentai plūsmai izmantojiet šo vienkāršoto tabulu:
| Caurules materiāls | Relatīvais raupjums (ε/D) | Berzes koeficients (λ) pie parastajiem Reinotsa skaitļiem |
|---|---|---|
| Re = 10 000 | ||
| Gludas caurules (PVC, poliuretāns) | 0.0001 – 0.0005 | 0.031 |
| Alumīnija caurules | 0.001 – 0.002 | 0.035 |
| Cinkots tērauds | 0.003 – 0.005 | 0.042 |
| Rūsējis tērauds | 0.01 – 0.05 | 0.054 |
Spiediena krituma aprēķināšana reālās pneimatiskajās sistēmās
Aplūkosim praktisku piemēru:
| Parametrs | Vērtība/aprēķins | Piemērs |
|---|---|---|
| Caurules diametrs (D) | Iekšējais diametrs | 8 mm (0,008 m) |
| Caurules garums (L) | Kopējais taisnais garums | 5m |
| Plūsmas ātrums (Q) | No sistēmas prasībām | 20 standarta litri sekundē |
| Gaisa blīvums (ρ) | Pie darba spiediena | 7,2 kg/m³ pie 6 bāriem |
| Plūsmas ātrums (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Reinoldsa skaitlis (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1 273 600 |
| Relatīvais raupjums | Poliuretāna caurulēm | 0.0003 |
| Berzes koeficients (λ) | No uzmeklēšanas tabulas | 0.017 |
| Spiediena kritums (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Reāla pielietošana: Cilindra ātruma problēmu risināšana
Pagājušajā gadā es strādāju kopā ar Sāru, ražošanas inženieri iepakojuma iekārtu uzņēmumā Viskonsīnā. Viņas balonu sistēma bez stieņiem darbojās tikai ar 60% no paredzētā ātruma, lai gan tai bija pareiza izmēra balons un atbilstošs padeves spiediens.
Analizējot viņas sistēmu, atklāju, ka viņa izmanto 6 mm caurules liela caurplūduma sistēmai. Berzes zudumi radīja 2,1 bāru spiediena kritumu, ievērojami samazinot pieejamo spēku un ātrumu. Pārejot uz 10 mm caurulēm, mēs samazinājām spiediena kritumu līdz 0,4 bāriem, un viņas sistēma nekavējoties sasniedza nepieciešamo veiktspēju bez jebkādām citām izmaiņām.
Faktori, kas ietekmē berzes zudumus reālās sistēmās
Faktiskos berzes zudumus ietekmē vairāki faktori:
- Gaisa temperatūra: Augstāka temperatūra palielina viskozitāti un berzi.
- Piesārņojums: Netīrumi un eļļa var palielināt faktisko raupjumu
- Cauruļu locīšana: Mikrodeformācija liektās caurulēs palielina pretestību
- Vecuma pasliktināšanās: Korozija un nogulsnes laika gaitā palielina raupjumu
- Darba spiediens: Augstāks spiediens palielina blīvumu un zudumus
Kāpēc ekvivalentā garuma metode ir kritiski svarīga precīzai sistēmas projektēšanai?
Vietējie zudumi veidgabalos, vārstos un līkumos bieži vien pārsniedz berzes zudumus taisnās caurulēs, tomēr daudzi inženieri tos ignorē vai arī izmanto aptuvenas novērtēšanas metodes, kas rada darbības problēmas.
Ar ekvivalentā garuma metodi vietējos zudumus, ko rada armatūra un vārsti, pārrēķina ekvivalentā taisnas caurules garumā, kas radītu tādu pašu spiediena kritumu. To aprēķina, izmantojot Le = K(D/λ), kur Le ir ekvivalents garums, K ir vietējo zudumu koeficients4, D ir caurules diametrs un λ ir berzes koeficients. Šī metode vienkāršo aprēķinus un nodrošina precīzāku sistēmas veiktspējas prognozēšanu.
Izpētīsim, kā šo metodi efektīvi izmantot pneimatisko sistēmu projektēšanā.
Biežāk sastopamo pneimatisko komponentu ekvivalenta garuma tabulas
Šeit ir praktiska uzziņu tabula par parastām pneimatikas sastāvdaļām:
| Sastāvdaļa | K-vērtība | Ekvivalents garums (Le/D) |
|---|---|---|
| 90° līkums (asais) | 0.9 | 30 |
| 90° līkums (standarta rādiuss) | 0.3 | 10 |
| 45° līkums | 0.2 | 7 |
| T-veida savienojums (caurplūdums) | 0.3 | 10 |
| T-veida savienojums (atzarojuma plūsma) | 1.0 | 33 |
| Lodveida vārsts (pilnībā atvērts) | 0.1 | 3 |
| Vārsts (pilnībā atvērts) | 0.2 | 7 |
| Ātrās savienošanas savienojums | 0.4-0.8 | 13-27 |
| Pārbaudes vārsts | 1.5-2.5 | 50-83 |
| Standarta plūsmas regulēšanas vārsts | 1.0-3.0 | 33-100 |
Ekvivalenta garuma metodes piemērošana
Lai efektīvi izmantotu šo metodi:
- Identificējiet visus pneimatiskās ķēdes komponentus.
- Katrai sastāvdaļai atrast K-vērtību vai ekvivalentā garuma attiecību (Le/D).
- Aprēķiniet ekvivalento garumu, reizinot ar caurules diametru.
- Pievienojiet visus ekvivalentos garumus faktiskajam taisnas caurules garumam.
- Berzes zudumu aprēķinos izmantojiet kopējo efektīvo garumu.
Piemēram, sistēma ar 5 m garu taisnu 8 mm cauruli un četriem 90° leņķa līkumiem, vienu T veida savienojumu un diviem ātrgaitas savienojumiem:
| Sastāvdaļa | Daudzums | Le/D | Ekvivalents garums |
|---|---|---|---|
| 90° līkumi | 4 | 10 | 4 × 10 × 0,008 m = 0,32 m |
| T-veida savienojums | 1 | 10 | 1 × 10 × 0,008 m = 0,08 m |
| Ātrie savienojumi | 2 | 20 | 2 × 20 × 0,008 m = 0,32 m |
| Kopējais ekvivalents garums | 0.72m | ||
| Faktiskais taisnais garums | 5.00m | ||
| Kopējais efektīvais garums | 5.72m |
Tas nozīmē, ka jūsu 5 m sistēma faktiski darbojas kā 5,72 m sistēma vietējo zudumu dēļ - efektīvais garums palielinās par 14,4%.
Gadījuma izpēte: Vārstu izvietojuma optimizācija montāžas sistēmās
Nesen palīdzēju Miguelam, automatizācijas inženierim elektronikas montāžas rūpnīcā Arizonā. Viņa komplektēšanas un ievietošanas sistēmā bija vērojamas nekonsekventas kustības un cikla laika svārstības, lai gan tika izmantoti augstas kvalitātes komponenti.
Analīze atklāja, ka viņa vārstu kolektors atradās 3 m attālumā no cilindriem, un ķēdē bija vairāki savienotājelementi. Ekvivalentā garuma aprēķins parādīja, ka viņa 3 m faktiskais attālums bija 7,2 m, jo radās vietējie zudumi - vairāk nekā divreiz lielāks nekā tiešās caurules attālums!
Pārvietojot vārstu kolektoru tuvāk cilindriem un likvidējot vairākus savienotājelementus, mēs samazinājām faktisko garumu no 7,2 m līdz 2,1 m. Tas samazināja spiediena kritumu par 70%, kā rezultātā tika panākta vienmērīga kustība un par 15% samazināts cikla laiks.
Praktiski padomi vietējo zaudējumu samazināšanai
Lai samazinātu vietējos zudumus pneimatiskajās sistēmās:
- Lietojiet izvērstus vai noapaļotus elkoņus asu līkumu vietā (samazina K-vērtību par 67%).
- Minimizēt veidgabalu skaitu plānojot tiešākus maršrutus
- Izvēlieties sastāvdaļas ar zemu sašaurinājumu piemēram, lodveida vārsti ar pilnu diametru, ja nepieciešams.
- Pareiza izmēra veidgabalu izvēle - nepietiekama izmēra veidgabali rada nesamērīgus zudumus.
- Novietojiet vārstus tuvu piedziņām lai līdz minimumam samazinātu efektīvo caurules garumu
Kas notiek, kad gaiss plūst caur samazinātām urbuma sekcijām?
Pneimatisko ķēžu samazinātas urbumu daļas - piemēram, daļēji aizvērti vārsti, nepietiekama izmēra savienotājelementi vai diametra pārejas - rada ievērojamus plūsmas ierobežojumus, kas var nopietni ietekmēt sistēmas veiktspēju.
Kad gaiss plūst cauri samazinātām urbuma sekcijām, spiediena kritumi5 notiek saskaņā ar formulu ΔP = ρ(v₂² - v₁²)/2, kur v₁ ir ātrums pirms ierobežojuma un v₂ ir ātrums ierobežojumā. To var kompensēt, izmantojot urbuma attiecības kompensācijas koeficientu C = (1 - (d/D)⁴), kur d ir samazinātais diametrs un D ir sākotnējais diametrs. Šis koeficients palīdz prognozēt faktisko sistēmas veiktspēju un izvairīties no komponentu nepietiekama izmēra.
Izpētīsim, kāda ir praktiskā ietekme uz samazinātu urbumu sekciju un kā to ņemt vērā, projektējot sistēmu.
Spiediena kritumu aprēķināšana diametra pārejās
Ja gaiss plūst no lielāka diametra uz mazāku, spiediena kritumu var aprēķināt, izmantojot:
| Parametrs | Formula | Piemērs |
|---|---|---|
| Sākotnējais diametrs (D) | No specifikācijām | 10 mm |
| Samazinātais diametrs (d) | No specifikācijām | 6 mm |
| Caurumu attiecība (d/D) | Vienkārša dalīšana | 0.6 |
| Plūsmas ātrums (Q) | No sistēmas prasībām | 15 standarta litri sekundē |
| Ātrums sākotnējā caurulē (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Ātrums samazinātā griezumā (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Spiediena kritums (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Kompensācijas koeficients (C) | C = (1 - (d/D)⁴) | 0.87 |
Biežāk sastopamie urbumu samazināšanas scenāriji un to ietekme
Lūk, kā dažādi urbumu samazinājumi ietekmē plūsmas caurlaides spēju:
| Caurumu samazināšana | Plūsmas jaudas samazināšana | Spiediena krituma palielināšanās |
|---|---|---|
| 10 mm līdz 8 mm | 36% | 2.4× |
| 10 mm līdz 6 mm | 64% | 7.7× |
| 10 mm līdz 4 mm | 84% | 39× |
| 8 mm līdz 6 mm | 44% | 3.2× |
| 8 mm līdz 4 mm | 75% | 16× |
| 6 mm līdz 4 mm | 56% | 5.1× |
Šie skaitļi parāda, kāpēc šķietami neliels diametra samazinājums var būtiski ietekmēt sistēmas veiktspēju.
Vairāku ierobežojumu kumulatīvā ietekme
Reālās pneimatiskajās ķēdēs vairāki ierobežojumi notiek virknē. To ietekme ir kumulatīva, un to var aprēķināt, izmantojot:
- Katra ierobežojuma konvertēšana ekvivalentā C-faktoram
- Aprēķiniet kopējo C-faktoru: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Izmantojiet šo kopējo koeficientu, lai noteiktu kopējo sistēmas veiktspējas samazinājumu.
Gadījuma izpēte: Vārstu un izpildmehānismu neatbilstības problēmu risināšana
Pagājušajā mēnesī es strādāju kopā ar Tomasu, tehniskās apkopes vadītāju mēbeļu ražotnē Ziemeļkarolīnā. Viņa jaunā cilindru sistēma bez stieņiem darbojās ar ātrumu, kas bija mazāks par pusi no paredzētā, lai gan tika izmantots ražotāja ieteiktais vārsta izmērs.
Izmeklēšana atklāja vairākus urbumu samazinājumus viņa ķēdē:
- 10 mm padeves līnija uz 8 mm vārsta atverēm (C₁ = 0,36)
- 8 mm vārsta porti uz 6 mm savienotājelementiem (C₂ = 0,44)
- 6 mm savienotājelementi uz 8 mm cilindra pieslēgvietām ar iekšējiem ierobežojumiem (C₃ = 0,32)
Kopējais kompensācijas koeficients bija Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32)(1-0,32) = 0,75, kas nozīmē, ka viņa sistēma zaudēja 75% no tās teorētiskās caurplūdes jaudas!
Modernizējot sistēmu ar atbilstoša izmēra komponentiem, mēs novērsām šos ierobežojumus un panācām nepieciešamo veiktspēju, nemainot balonu vai padeves spiedienu.
Praktiskas stratēģijas urbumu samazināšanas zudumu samazināšanai līdz minimumam
Lai samazinātu urbumu samazināšanas radītos zaudējumus:
- Konsekvents komponentu izmērs visā pneimatiskajā ķēdē
- Izmantojiet lielāko praktisko cauruļu izmēru liela caurplūduma lietojumiem
- Pievērsiet uzmanību iekšējiem komponentu ierobežojumiem, ne tikai savienojumu izmēri
- Apsveriet paralēlus plūsmas ceļus augsta caurplūduma prasībām
- Novērst nevajadzīgus adapterus un pārejas ja iespējams.
"Vājākā posma" princips pneimatiskajās sistēmās
Atcerieties, ka pneimatiskās sistēmas veiktspēju ierobežo tās ierobežojošākā sastāvdaļa. Viens nepietiekami izmērīts elements var izjaukt priekšrocības, ko sniedz pareizi izmērīti komponenti citur sistēmā.
Piemēram, sistēma ar 10 mm caurulēm, 10 mm vārstiem, bet 6 mm savienotājelementiem pie cilindra darbosies pēc būtības tāpat kā sistēma ar 6 mm komponentiem visā sistēmā, taču tās izmaksas būs lielākas.
Secinājums
Izpratne par plūsmas pretestību un tās pareiza aprēķināšana, izmantojot berzes koeficientu tabulas, ekvivalentā garuma metodes un samazināta urbuma kompensāciju, ir būtiska, lai projektētu pneimatiskās sistēmas, kas reālos apstākļos darbotos, kā paredzēts. Izmantojot šīs aprēķinu metodes un projektēšanas principus, varat optimizēt bezvārpstu cilindru lietojumus un citas pneimatiskās sistēmas, lai nodrošinātu maksimālu veiktspēju un uzticamību.
Bieži uzdotie jautājumi par plūsmas pretestību pneimatiskajās sistēmās
Cik liels spiediena kritums ir pieļaujams pneimatiskajā sistēmā?
Pieļaujamais spiediena kritums ir atkarīgs no jūsu lietojuma prasībām, bet, lai nodrošinātu efektīvu darbību, kā vispārīgu vadlīniju var izmantot ierobežojumu, kas paredz kopējo spiediena kritumu līdz 10-15% no padeves spiediena. 6 bāru sistēmai tas nozīmē, ka kopējais spiediena kritums nedrīkst pārsniegt 0,6-0,9 bārus. Kritiskiem lietojumiem var būt nepieciešams vēl mazāks spiediena kritums - 5-8%, lai saglabātu nemainīgu veiktspēju.
Kāda ir saistība starp caurules diametru un spiediena kritumu?
Spiediena kritums ir apgriezti proporcionāls diametra piektajai pakāpei (D⁵), ja plūsma pneimatiskajās sistēmās ir turbulenta. Tas nozīmē, ka caurules diametra divkāršošana samazina spiediena kritumu aptuveni 32 reizes. Piemēram, palielinot caurules diametru no 6 mm līdz 12 mm, var samazināt spiediena kritumu no 1,5 bāriem līdz tikai 0,047 bāriem tādos pašos plūsmas apstākļos.
Kā noteikt pareizo caurules izmēru savam pneimatiskajam lietojumam?
Izvēlieties caurules izmēru, pamatojoties uz plūsmas ātruma prasībām un pieļaujamo spiediena kritumu. Aprēķiniet Reinoldsa skaitli un berzes koeficientu, pēc tam izmantojiet Darcy-Weisbach vienādojumu, lai noteiktu spiediena kritumu dažādiem diametriem. Izvēlieties mazāko diametru, kas nodrošina spiediena kritumu pieņemamās robežās (parasti <10% no padeves spiediena), vienlaikus ņemot vērā vietas ierobežojumus un izmaksas.
Kas rada vairāk ierobežojumu: 90° leņķa līkums vai 5 metri taisnas caurules?
Ass 90° leņķa līkums parasti rada pretestību, kas līdzvērtīga 30 taisnas caurules diametru pretestībai. Attiecībā uz 8 mm caurulēm viens asais līkums atbilst aptuveni 240 mm (30 × 8 mm) taisnas caurules diametram. Tas nozīmē, ka 5 metri taisnas caurules rada aptuveni 21 reizi lielāku ierobežojumu nekā viens līkums. Tomēr sistēmās bieži vien ir vairāki līkumi un savienotājelementi, kuru kumulatīvais efekts var pārsniegt taisnās caurules garuma zudumus.
Kā ātri savienojamie savienotājelementi ietekmē sistēmas veiktspēju?
Standarta ātrās savienošanas savienotājelementi parasti rada vietējos zudumus, kas ir līdzvērtīgi 15-25 caurules diametriem taisnās caurulēs. Vēl būtiskāk ir tas, ka daudziem ātrgaitas savienojumiem ir iekšējie ierobežojumi, kas ir mazāki par to nominālo izmēru. "10 mm" ātrajam savienojumam var būt tikai 7-8 mm iekšējais ierobežojums, tādējādi radot urbuma samazinājumu, kas var samazināt plūsmas caurlaides spēju par 50-70% šajā punktā.
Kāda ir daļēji aizvērtu plūsmas regulēšanas vārstu ietekme uz sistēmas veiktspēju?
Plūsmas regulēšanas vārsts, kas ir aizvērts līdz 50% no pilnas urbuma platības, nesamazina plūsmu tikai par 50% - tas samazina plūsmu par aptuveni 75% nelineārās sakarības starp diametru un plūsmas jaudu dēļ. Spiediena kritums palielinās atbilstoši ātruma izmaiņu kvadrātam, tāpēc, samazinot efektīvo diametru uz pusi, spiediena kritums palielinās aptuveni 16 reižu pie tādiem pašiem plūsmas nosacījumiem.
-
Sniedz detalizētu Darcy-Weisbach vienādojuma, kas ir fundamentāla un plaši izmantota formula šķidrumu dinamikā, lai aprēķinātu spiediena zudumus berzes dēļ caurulē, sadalījumu. ↩
-
Piedāvā skaidru Reinolda skaitļa definīciju, kas ir kritisks bezdimensiju lielums, ko izmanto, lai prognozētu plūsmas modeļus (lamināras vai turbulentas) dažādās šķidruma plūsmas situācijās. ↩
-
Sniedz Mūdija diagrammu - visaptverošu grafiku, kurā Darcy berzes koeficients ir attēlots atkarībā no Reinoldsa skaitļa un relatīvā raupjuma, kas ir standarta rīks inženieriem, lai noteiktu spiediena kritumu caurulēs. ↩
-
Paskaidro K vērtības jeb vietējo zudumu koeficienta jēdzienu, kas ir bezizmēra skaitlis, ko izmanto, lai raksturotu spiediena zudumus cauruļu veidgabalā vai vārstā kā daļu no ekvivalentā garuma metodes. ↩
-
Detalizēti apraksta fizikālās īpašības, kas nosaka spiediena kritumu, kurš rodas, šķidrumam plūstot caur ierobežojumu (atveri), pamatojoties uz nepārtrauktības vienādojuma un Bernuļa principa principiem. ↩



