Projektējot pneimatisko cilindru sistēmas, inženieri bieži vien nepareizi aprēķina stieņu laukumus, kas izraisa nepareizus spēka aprēķinus un sistēmas darbības traucējumus.
Stieņa laukums ir apaļā šķērsgriezuma laukums, ko aprēķina kā A = πr² vai A = π(d/2)², kur "r" ir stieņa rādiuss un "d" ir stieņa diametrs, kas ir kritisks spēka un spiediena aprēķinos.
Vakar es palīdzēju Karlosam, projektēšanas inženierim no Meksikas, kura pneimatiskā sistēma neizdevās, jo viņš divpusējas darbības cilindra spēka aprēķinos aizmirsa atņemt stieņa laukumu no virzuļa laukuma.
Satura rādītājs
- Kas ir stieņa laukums pneimatisko cilindru sistēmās?
- Kā aprēķināt stieņa šķērsgriezuma laukumu?
- Kāpēc stieņa laukums ir svarīgs spēka aprēķinos?
- Kā stieņa laukums ietekmē cilindra veiktspēju?
Kas ir stieņa laukums pneimatisko cilindru sistēmās?
Virzuļa laukums ir virzuļa stieņa apaļā šķērsgriezuma laukums, kas ir būtisks, lai aprēķinātu efektīvos virzuļa laukumus un spēka izvades jaudu divpusējas darbības pneimatiskajos cilindros.
Stieņa laukums ir virzuļa stieņa šķērsgriezuma apaļais laukums, ko mēra perpendikulāri stieņa asij un ko izmanto, lai noteiktu neto efektīvo laukumu spēka aprēķiniem.
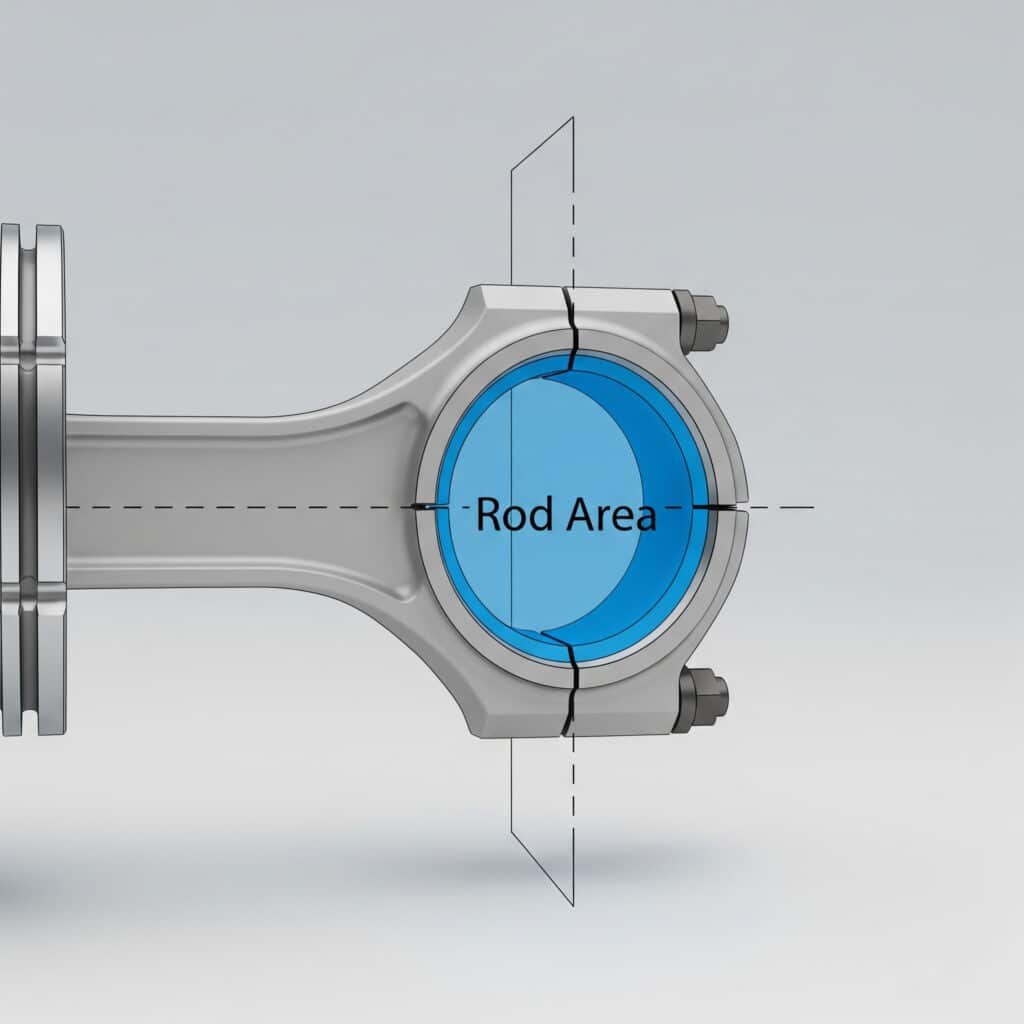
Stieņa laukuma definīcija
Ģeometriskās īpašības
- Apļveida šķērsgriezums: Standarta stieņa ģeometrija
- Perpendikulārais mērījums: 90° leņķī pret stieņa centra līniju
- Nemainīga platība: Vienmērīga stieņa garumā
- Cietā zona: Pilns materiāla šķērsgriezums
Galvenie mērījumi
- Stieņa diametrs: Platības aprēķina pamatdimensija
- Stieņa rādiuss: Puse no diametra mērījuma
- Šķērsgriezuma laukums: Apļveida apgabala formulas piemērošana
- Efektīvā platība: Ietekme uz balona veiktspēju
Stieņa un virzuļa laukuma attiecība
| Sastāvdaļa | Platības formula | Mērķis | Pieteikums |
|---|---|---|---|
| Virzuļa | A = π(D/2)² | Pilna urbuma zona | Paplašināt spēka aprēķinu |
| Rod | A = π(d/2)² | Stieņa šķērsgriezums | Atvilkšanas spēka aprēķins |
| Neto platība | A_pistons - A_stienis | Efektīva ievilkšanas zona | Divpusējas darbības cilindri |
| Stūra laukums1 | π(D² - d²)/4 | Gredzenveida zona | Stieņa puses spiediens |
Standarta stieņu izmēri
Parastie stieņu diametri
- 8 mm stienis: Platība = 50,3 mm²
- 12 mm stienis: Platība = 113,1 mm²
- 16 mm stienis: Platība = 201,1 mm²
- 20 mm stienis: Platība = 314,2 mm²
- 25 mm stienis: Platība = 490,9 mm²
- 32 mm stienis: Platība = 804,2 mm²
Stieņa un urbuma attiecība
- Standarta attiecība: stieņa diametrs = 0,5 × urbuma diametrs
- Lieljaudas: stieņa diametrs = 0,6 × urbuma diametrs
- Vieglā slodze: stieņa diametrs = 0,4 × urbuma diametrs
- Pielāgotas lietojumprogrammas: Atkarībā no prasībām
Stieņa zonas lietojumprogrammas
Spēka aprēķini
Es izmantoju stieņa laukumu, lai:
- Paplašināt spēku: Pilna virzuļa laukums × spiediens
- Atvilkšanas spēks: (virzuļa laukums - stieņa laukums) × spiediens
- Spēka starpība: Atšķirība starp pagarināt/atvilkt
- Slodzes analīze: Cilindra atbilstība lietojumam
Sistēmas izstrāde
Stieņa platība ietekmē:
- Cilindru izvēle: Pareiza izmēra noteikšana lietojumiem
- Ātruma aprēķini: Plūsmas prasības katram virzienam
- Spiediena prasības: Sistēmas spiediena specifikācijas
- Veiktspējas optimizācija: Līdzsvarota darbības konstrukcija
Stieņa laukums dažādos cilindru tipos
Viendarbības cilindri
- Nav ietekmes uz stieņa laukumu: Atsperes atgriešanās darbība
- Tikai pagarināt spēku: Pilna virzuļa laukuma efektivitāte
- Vienkāršoti aprēķini: Nav apsvērumu par ievilkšanas spēku
- Izmaksu optimizācija: Samazināta sarežģītība
Divpusējas darbības cilindri
- Stieņa platība ir kritiska: Ietekmē ievilkšanas spēku
- Asimetriska darbība: Dažādi spēki katrā virzienā
- Sarežģīti aprēķini: Jāņem vērā abas jomas
- Veiktspējas līdzsvarošana: Nepieciešamie dizaina apsvērumi
Cilindri bez stieņiem
- Nav stieņa zonas: Izslēgts no konstrukcijas
- Simetriska darbība: Vienādi spēki abos virzienos
- Vienkāršoti aprēķini: Viena apgabala apsvērumi
- Telpas priekšrocības: Stieņa pagarināšanas prasību nav
Kā aprēķināt stieņa šķērsgriezuma laukumu?
Stieņa šķērsgriezuma laukuma aprēķinā izmanto standarta apļa laukuma formulu ar stieņa diametra vai rādiusa mērījumiem, lai precīzi projektētu pneimatisko sistēmu.
Aprēķiniet stieņa laukumu, izmantojot A = πr² (ar rādiusu) vai A = π(d/2)² (ar diametru), kur π = 3,14159, nodrošinot vienotas mērvienības visā aprēķina gaitā.
Platības pamatformula
Stieņa rādiusa izmantošana
A = πr²
- A: Stieņa šķērsgriezuma laukums
- π: 3,14159 (matemātiskā konstante)
- r: Stieņa rādiuss (diametrs ÷ 2)
- Vienības: Platība rādiusa vienībās kvadrātā
Stieņa diametra izmantošana
A = π(d/2)² vai A = πd²/4
- A: Stieņa šķērsgriezuma laukums
- π: 3.14159
- d: Stieņa diametrs
- Vienības: Platība diametra vienībās kvadrātā
Pakāpenisks aprēķins
Mērīšanas process
- Izmēriet stieņa diametru: Lai nodrošinātu precizitāti, izmantojiet suporti
- Pārbaudīt mērījumus: Veikt vairākus nolasījumus
- Aprēķināt rādiusu: r = diametrs ÷ 2 (ja izmanto rādiusa formulu)
- Piemērot formulu: A = πr² vai A = π(d/2)²
- Pārbaudes vienības: Nodrošināt konsekventu vienību sistēmu
Aprēķina piemērs
20 mm diametra stienim:
- 1. metode: A = π(10)² = π × 100 = 314,16 mm²
- 2. metode: A = π(20)²/4 = π × 400/4 = 314,16 mm²
- Verifikācija: Abas metodes sniedz identiskus rezultātus
Stieņa laukuma aprēķina tabula
| Stieņa diametrs | Stieņa rādiuss | Platības aprēķināšana | Stieņa laukums |
|---|---|---|---|
| 8 mm | 4 mm | π × 4² | 50,3 mm² |
| 12 mm | 6 mm | π × 6² | 113,1 mm² |
| 16 mm | 8 mm | π × 8² | 201,1 mm² |
| 20 mm | 10 mm | π × 10² | 314,2 mm² |
| 25 mm | 12,5 mm | π × 12.5² | 490,9 mm² |
| 32 mm | 16 mm | π × 16² | 804,2 mm² |
Mērīšanas rīki
Digitālie suporti
- Precizitāte: ±0,02 mm precizitāte
- Diapazons: 0-150 mm tipisks
- Funkcijas: Digitālais displejs, vienību konvertēšana
- Labākā prakse: Vairāki mērījumu punkti
Mikrometrs
- Precizitāte: ±0,001 mm precizitāte
- Diapazons: Pieejami dažādi izmēri
- Funkcijas: Sprūdrata fiksators, digitālās opcijas
- Pieteikumi: Augstas precizitātes prasības
Biežāk sastopamās aprēķinu kļūdas
Mērīšanas kļūdas
- Diametrs pret rādiusu: Nepareizas dimensijas izmantošana formulā
- Vienības nekonsekvence: mm un collu sajaukšana
- Precizitātes kļūdas: Nepietiekami daudz zīmju aiz komata
- Instrumentu kalibrēšana: Nekalibrēti mērinstrumenti
Formulas kļūdas
- Nepareiza formula: Apjoma izmantošana laukuma vietā
- Trūkst π: Aizmirstot matemātisko konstanti
- Kļūdu izlīdzināšana: Nepareiza eksponenta piemērošana
- Vienību konvertēšana: Nepareizas vienību transformācijas
Verifikācijas metodes
Krustpārbaudes metodes
- Vairāki aprēķini: Dažādas formulas metodes
- Mērījumu verifikācija: Atkārtot diametra mērījumus
- Atsauces tabulas: Salīdziniet ar standarta vērtībām
- CAD programmatūra: 3D modeļa platības aprēķini
Pamatotības pārbaudes
- Izmēra korelācija: Lielāks diametrs = lielāks laukums
- Standarta salīdzinājumi: Atbilst tipiskiem stieņu izmēriem
- Piemērotība lietošanai: Atbilstoši balona izmēram
- Ražošanas standarti: Kopējie pieejamie izmēri
Uzlabotie aprēķini
Dobi stieņi
A = π(D² - d²)/4
- D: Ārējais diametrs
- d: Iekšējais diametrs
- Pieteikums: Svara samazināšana, iekšējā maršrutēšana
- Aprēķins: Iekšējā laukuma atņemšana no ārējā laukuma
Ne-apļveida stieņi
- Kvadrātveida stieņi: A = puse²
- Taisnstūrveida stieņi: A = garums × platums
- Īpašas formas: Izmantot atbilstošas ģeometriskās formulas
- Pieteikumi: Novērst rotāciju, īpašas prasības
Kad strādāju ar Dženiferu, pneimatisko sistēmu projektētāju no Kanādas, viņa sākotnēji nepareizi aprēķināja stieņa laukumu, izmantojot diametru, nevis rādiuss πr² formulā, kā rezultātā tika iegūts 4 reizes pārvērtēts un pilnīgi nepareizi aprēķināts spēks divpusējas darbības cilindra lietojumam.
Kāpēc stieņa laukums ir svarīgs spēka aprēķinos?
Stieņa laukums tieši ietekmē efektīvu virzuļa laukumu divpusējas darbības cilindru stieņa pusē, radot spēka atšķirības starp izvilkšanas un ievilkšanas operācijām.
Stieņa laukums samazina efektīvu virzuļa laukumu ievilkšanas laikā, radot mazāku ievilkšanas spēku salīdzinājumā ar izvilkšanas spēku divpusējas darbības cilindros, kas prasa kompensāciju sistēmas konstrukcijā.
Spēka aprēķināšanas pamati
Pamatspēka formula
- Paplašināt spēku: F = P × A_pistons
- Atvilkšanas spēks: F = P × (A_stūmējs - A_stūmējs)
- Spēka starpība: Izstiepšanas spēks > Atvilkšanas spēks
- Dizaina ietekme: Jāņem vērā abi virzieni
Efektīvās jomas
- Pilns virzuļa laukums: Pieejams pagarinājuma laikā
- Virzuļa neto laukums: Virzuļa laukums mīnus stieņa laukums ievilkšanas laikā
- Stūra laukums: Gredzena formas laukums stieņa pusē
- Platības attiecība: Nosaka spēka starpību
Spēka aprēķina piemēri
63 mm diametra urbums, 20 mm stieņa cilindrs
- Virzuļa laukums: π(31,5)² = 3,117 mm²
- Stieņa laukums: π(10)² = 314 mm²
- Neto platība: 3 117 - 314 = 2 803 mm²
- Pie 6 bāru spiediena:
– Paplašināt spēku: 6 × 3,117 = 18,702 N
– Atvilkšanas spēks: 6 × 2,803 = 16,818 N
– Spēka starpība: 1,884 N (10% samazinājums)
Spēka salīdzināšanas tabula
| Cilindra izmērs | Virzuļa laukums | Stieņa laukums | Neto platība | Spēka attiecība |
|---|---|---|---|---|
| 32 mm/12 mm | 804 mm² | 113 mm² | 691 mm² | 86% |
| 50 mm/16 mm | 1 963 mm² | 201 mm² | 1,762 mm² | 90% |
| 63 mm/20 mm | 3 117 mm² | 314 mm² | 2 803 mm² | 90% |
| 80 mm/25 mm | 5,027 mm² | 491 mm² | 4 536 mm² | 90% |
| 100 mm/32 mm | 7 854 mm² | 804 mm² | 7 050 mm² | 90% |
Pieteikuma ietekme
Slodzes saskaņošana
- Paplašināt slodzes: Iztur pilnu nominālo spēku
- Ielieciet slodzes: Ierobežota efektīvā platība
- Slodzes līdzsvarošana: Ņemiet vērā spēka starpību projektēšanā
- Drošības rezerves: Samazinātās ievilkšanas spējas ņemšana vērā
Sistēmas veiktspēja
- Ātruma atšķirības: Dažādas plūsmas prasības katrā virzienā
- Spiediena prasības: Var būt nepieciešams lielāks spiediens ievilkšanai
- Kontroles sarežģītība: Asimetriskas darbības apsvērumi
- Energoefektivitāte: Optimizēt abos virzienos
Dizaina apsvērumi
Stieņa izmēra izvēle
- Standarta koeficienti: stieņa diametrs = 0,5 × urbuma diametrs
- Smagās kravas: Lielāks stienis konstrukcijas izturībai
- Spēka līdzsvars: Mazāks stienis vienādākiem spēkiem
- Pielietojumam specifisks: Pielāgotie koeficienti īpašām prasībām
Spēka līdzsvarošanas stratēģijas
- Spiediena kompensācija: Augstāks spiediens stieņa pusē
- Platībatkarīgā kompensācija: Lielāks cilindrs ievilkšanas prasībām
- Divi cilindri: Atsevišķi cilindri katram virzienam
- Konstrukcija bez stieņiem: Novērst stienīšu zonas ietekmi
Praktiskie lietojumi
Materiālu apstrāde
- Pacelšanas lietojumprogrammas: Paplašināt spēka kritisko
- Stumšanas operācijas: Var būt nepieciešama savilkšanas spēka saskaņošana
- Saspiešanas sistēmas: Spēka starpība ietekmē turēšanas jaudu
- Pozicionēšanas precizitāte: Spēka svārstības ietekmē precizitāti
Ražošanas procesi
- Preses operācijas: Konsekventas spēka prasības
- Montāžas sistēmas: Nepieciešama precīza spēka kontrole
- Kvalitātes kontrole: Spēka variācijas ietekmē produkta kvalitāti
- Cikla ilgums: Spēka atšķirības ietekmes ātrums
Force problēmu novēršana
Bieži sastopamās problēmas
- Nepietiekams ievilkšanas spēks: Tīkla platībai pārāk liela slodze
- Nevienmērīga darbība: Spēka starpība rada problēmas
- Ātruma izmaiņas: Dažādas plūsmas prasības
- Kontroles grūtības: Asimetriskas reakcijas raksturlielumi
Risinājumi
- Cilindru izmēru palielināšana: Lielāks urbums atbilstošam ievilkšanas spēkam.
- Spiediena regulēšana: Optimizēt kritisko virzienu
- Stieņa izmēra optimizācija: Līdzsvara spēks pret spēka prasībām
- Sistēmas pārprojektēšana: Apsveriet alternatīvas bez stieņiem
Kad es konsultējos ar Maikls, mašīnbūves meistaru no Austrālijas, viņa iepakošanas iekārtas darbojās nekonsekventi, jo viņš bija projektējis tikai izstiepšanas spēka pielietošanai. 15% ievilkšanas spēka samazinājums izraisīja aizķeršanos atgriešanās gājiena laikā, tāpēc bija nepieciešams palielināt cilindra izmērus, lai pareizi darbotos abos virzienos.
Kā stieņa laukums ietekmē cilindra veiktspēju?
Pneimatiskajos lietojumos stieņa laukums būtiski ietekmē cilindra ātrumu, izejas spēku, enerģijas patēriņu un kopējo sistēmas veiktspēju.
Lielāki stieņa laukumi samazina ievilkšanas spēku un palielina ievilkšanas ātrumu, jo ir mazāks efektīvais laukums un mazāks nepieciešamais gaisa tilpums, radot asimetriskas cilindra darbības īpašības.
Ātruma veiktspējas ietekme
Plūsmas ātruma attiecības
Ātrums = Plūsmas ātrums3 ÷ efektīvais laukums
- Paplašināt ātrumu: Plūsma ÷ pilna virzuļa laukums
- Atvilkšanas ātrums: Plūsma ÷ (virzuļa laukums - stieņa laukums)
- Ātruma starpība: Atvilkt parasti ātrāk
- Plūsmas optimizācija: Atšķirīgas prasības katrā virzienā
Ātruma aprēķina piemērs
63 mm caurulei, 20 mm stienis ar 100 L/min plūsmu:
- Paplašināt ātrumu: 100 000 ÷ 3 117 = 32,1 mm/s
- Atvilkšanas ātrums: 100 000 ÷ 2 803 = 35,7 mm/s
- Ātruma palielināšana: 11% ātrāka ievilkšana
Veiktspējas raksturlielumi
Spēka izejas efekti
| Stieņa izmērs | Spēka samazināšana | Ātruma palielināšana | Ietekme uz veiktspēju |
|---|---|---|---|
| Mazs (d/D = 0,3) | 9% | 10% | Minimāla asimetrija |
| Standarta (d/D = 0,5) | 25% | 33% | Mērena asimetrija |
| Liels (d/D = 0,6) | 36% | 56% | Ievērojama asimetrija |
Enerģijas patēriņš
- Pagarināt insultu: Nepieciešams pilns gaisa tilpums
- Atvilkšanas gājiens: Samazināts gaisa tilpums (stieņa pārvietojums)
- Enerģijas ietaupījums: Mazāks patēriņš ievilkšanas laikā
- Sistēmas efektivitāte: Iespējama vispārēja enerģijas optimizācija
Gaisa patēriņa analīze
Tilpuma aprēķini
- Paplašināt apjomu: Virzuļa laukums × gājiena garums
- Atvilkt tilpumu: (virzuļa laukums - stieņa laukums) × gājiena garums
- Tilpuma starpība: Stieņu apjoma ietaupījums
- Izmaksu ietekme: Samazinātas kompresora prasības
Patēriņa piemērs
100 mm urbums, 32 mm stienis, 500 mm gājiens:
- Paplašināt apjomu: 7,854 × 500 = 3,927,000 mm³
- Atvilkt tilpumu: 7,050 × 500 = 3,525,000 mm³
- Uzkrājumi: 402 000 mm³ (10% samazinājums)
Sistēmas dizaina optimizācija
Stieņa izmēra izvēles kritēriji
- Strukturālās prasības: Izlieces4 un lieces slodzes
- Spēka līdzsvars: Pieņemama spēka starpība
- Ātruma prasības: Vēlamie ātruma raksturlielumi
- Energoefektivitāte: Gaisa patēriņa optimizācija
- Izmaksu apsvērumi: Materiālu un ražošanas izmaksas
Veiktspējas līdzsvarošana
- Plūsmas kontrole: Atsevišķa regula katram virzienam
- Spiediena kompensācija: Pielāgojiet spēka prasībām
- Ātruma saskaņošana: Ja nepieciešams, droseles ātrāks virziens
- Slodzes analīze: Cilindra atbilstība lietojumprogrammas prasībām
Īpaši lietojumprogrammas apsvērumi
Ātrgaitas lietojumprogrammas
- Mazie stieņi: Minimizēt ātruma starpību
- Plūsmas optimizācija: Katra virziena vārstu izmēri
- Kontroles sarežģītība: Asimetriskās reakcijas pārvaldība
- Precizitātes prasības: Ātruma svārstību ņemšana vērā
Lielas noslodzes lietojumprogrammas
- Lieli stieņi: Konstrukcijas stiprības prioritāte
- Spēka kompensācija: Pieņemt samazinātu ievilkšanas spēku
- Slodzes analīze: Nodrošināt atbilstošas iespējas abos virzienos
- Drošības faktori: Konservatīva dizaina pieeja
Veiktspējas uzraudzība
Galvenie darbības rādītāji
- Cikla laika konsekvence: Uzraudzīt ātruma svārstības
- Spēka izvade: Pārbaudīt atbilstošas spējas
- Enerģijas patēriņš: Izsekojiet gaisa izmantošanas modeļus
- Sistēmas spiediens: Optimizēt efektivitāti
Problēmu novēršanas vadlīnijas
- Lēna ievilkšana: Pārbaudiet, vai nav pārmērīga stieņa laukuma
- Nepietiekams spēks: Faktiskās platības aprēķinu pārbaude
- Nevienmērīgs ātrums: Noregulējiet plūsmas regulēšanas ierīces
- Liels enerģijas patēriņš: Optimizēt stieņa izmēra izvēli
Uzlabotas veiktspējas koncepcijas
Dinamiskā reakcija
- Paātrinājuma atšķirības: Masas un zonas ietekme
- Rezonanses raksturlielumi: Dabiskās frekvences svārstības
- Kontroles stabilitāte: Asimetriska sistēmas uzvedība
- Pozicionēšanas precizitāte: Ātruma starpības ietekme
Siltuma ietekme
- Siltuma ražošana: Augstāks pagarinājuma virzienā
- Temperatūras paaugstināšanās: Ietekmē darbības konsekvenci
- Dzesēšanas prasības: Var būt nepieciešama uzlabota siltuma izkliedēšana
- Materiāla paplašināšanās: Siltuma pieauguma apsvērumi
Reālās darbības dati
Gadījuma izpētes rezultāti
Analizējot 100 instalācijas, tika konstatēts, ka:
- Standarta stieņu attiecība: 10-15% ātruma starpība tipiska
- Lielizmēra stieņi: Līdz 50% ātruma palielinājums ievelkot
- Mazizmēra stieņi: Strukturālās kļūmes 25% gadījumu
- Optimizēti dizaini: Sasniedzama līdzsvarota veiktspēja
Kad optimizēju cilindra izvēli Lizai, iepakojuma inženierei no Apvienotās Karalistes, mēs samazinājām stieņa izmēru no 0,6 līdz 0,5 urbuma attiecībai, uzlabojot spēka līdzsvaru par 20%, vienlaikus saglabājot atbilstošu strukturālo izturību un samazinot cikla laika izmaiņas par 30%.
Secinājums
Stieņa laukums ir π(d/2)², izmantojot stieņa diametru "d". Šis laukums samazina efektīvo ievilkšanas spēku divpusējas darbības cilindros, radot ātruma un spēka atšķirības, kas jāņem vērā, projektējot pneimatisko sistēmu.
Bieži uzdotie jautājumi par stieņu zonu
Kā aprēķināt stieņa laukumu?
Aprēķiniet stieņa laukumu, izmantojot A = π(d/2)², kur "d" ir stieņa diametrs, vai A = πr², kur "r" ir stieņa rādiuss. 20 mm diametra stienim: A = π(10)² = 314,2 mm².
Kāpēc pneimatiskajos cilindros ir svarīga stieņa laukums?
Stieņa laukums samazina efektīvu virzuļa laukumu divpusējas darbības cilindru ievilkšanas laikā, radot mazāku ievilkšanas spēku salīdzinājumā ar izvilkšanas spēku. Tas ietekmē spēka aprēķinus, ātruma raksturlielumus un sistēmas veiktspēju.
Kā stieņa laukums ietekmē cilindra spēku?
Stieņa laukums samazina ievilkšanas spēku par attiecīgo daudzumu: Spriegums = spiediens × (virzuļa laukums - stieņa laukums). 20 mm stienis 63 mm cilindrā samazina ievilkšanas spēku par aptuveni 10% salīdzinājumā ar izvilkšanas spēku.
Kas notiek, ja aprēķinos neņem vērā stieņa laukumu?
Stieņa laukuma ignorēšana noved pie pārvērtētiem vilkšanas spēka aprēķiniem, nepietiekama izmēra cilindru vilkšanas slodzēm, nepareizām ātruma prognozēm un iespējamām sistēmas kļūmēm, ja faktiskā veiktspēja neatbilst projektētajām.
Kā stieņa izmērs ietekmē cilindra veiktspēju?
Lielāki stieņi vairāk samazina ievilkšanas spēku, bet palielina ievilkšanas ātrumu, jo ir mazāks efektīvais laukums. Standarta stieņu attiecība (d/D = 0,5) nodrošina labu līdzsvaru starp konstrukcijas izturību un spēka simetriju lielākajā daļā lietojumu.
-
Izpratne par gredzenveida laukuma definīciju un aprēķināšanu inženiertehniskajā kontekstā. ↩
-
Izpētiet fizikas pamatprincipu - Paskāla likumu, kas nosaka šķidrumu enerģijas sistēmu darbību. ↩
-
Iepazīstieties ar konstrukcijas izlieces principiem, kas ir kritisks bojājuma veids tievām detaļām, kuras tiek saspiestas. ↩
-
Apskatiet plūsmas ātruma definīciju un tā nozīmi ātruma aprēķināšanā šķidrumu sistēmās. ↩




