Sliter du med lave sylinderhastigheter, inkonsekvente bevegelser eller utilstrekkelig kraft i de pneumatiske systemene dine? Disse vanlige problemene skyldes ofte en misforstått årsak: strømningsmotstand. Mange ingeniører dimensjonerer pneumatiske komponenter utelukkende basert på trykk- og kraftkrav, og overser den kritiske effekten strømningsmotstanden har på ytelsen i den virkelige verden.
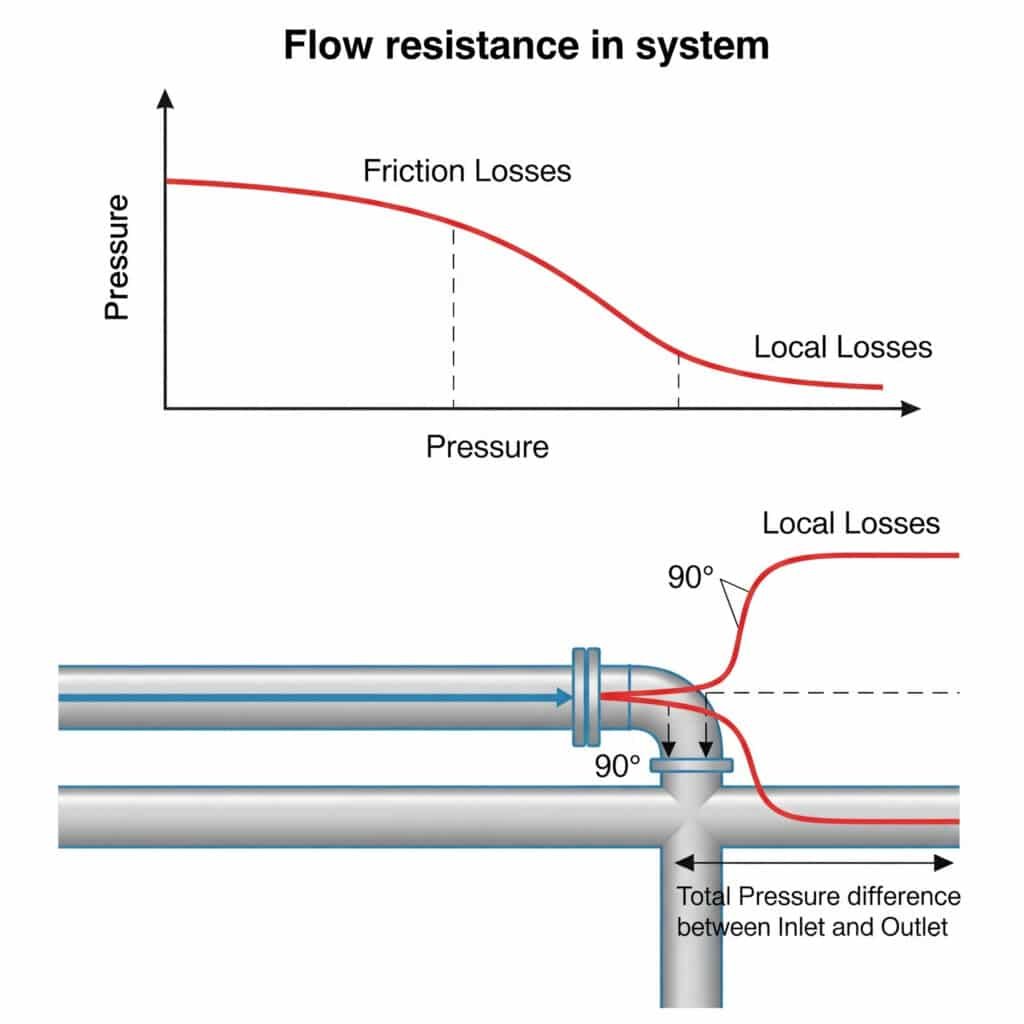
Strømningsmotstand i pneumatiske systemer skaper trykkfall som reduserer tilgjengelig kraft, begrenser maksimal hastighet og forårsaker inkonsekvent bevegelse. Denne motstanden kommer både fra friksjon langs rette rør (friksjonstap) og forstyrrelser ved koblinger, bend og ventiler (lokale tap). Til sammen kan disse motstandene redusere den faktiske systemytelsen med 20-50% sammenlignet med teoretiske beregninger.
I løpet av de mer enn 15 årene jeg har jobbet med pneumatiske systemer i Bepto, har jeg sett utallige tilfeller der forståelse og håndtering av strømningsmotstand har forvandlet underpresterende systemer til pålitelige og effektive operasjoner. La meg dele det jeg har lært om hvordan man beregner og minimerer disse skjulte ytelsesdriverne.
Innholdsfortegnelse
- Hvordan beregner man egentlig friksjonstap i pneumatiske ledninger?
- Hvorfor er metoden for ekvivalent lengde avgjørende for nøyaktig systemdesign?
- Hva skjer når luft strømmer gjennom reduserte boreseksjoner?
- Konklusjon
- Vanlige spørsmål om strømningsmotstand i pneumatiske systemer
Hvordan beregner man egentlig friksjonstap i pneumatiske ledninger?
Friksjonstap i rette rør og slanger er grunnlaget for beregninger av strømningsmotstand, men mange ingeniører baserer seg på overforenklede tommelfingerregler som fører til underdimensjonerte systemer.
Friksjonstap i pneumatiske ledninger beregnes ved hjelp av Darcy-Weisbach-ligningen1ΔP = λ(L/D)(ρv²/2), der λ er friksjonsfaktoren, L er rørlengden, D er rørdiameteren, ρ er lufttettheten og v er strømningshastigheten. For pneumatiske systemer varierer friksjonsfaktoren λ basert på Reynolds tall2 og relativ ruhet, og bestemmes vanligvis ved hjelp av oppslagstabeller eller Moody-diagram3.
Å forstå friksjonstap har praktiske konsekvenser for systemdesign og feilsøking. La meg bryte dette ned i praktisk anvendelig innsikt.
Effektiv bruk av friksjonsfaktortabeller
Friksjonsfaktoren (λ) er nøkkelparameteren ved beregning av trykkfall, men for å bestemme verdien må man ta hensyn til strømningsforholdene:
| Strømningsregime | Reynolds tall (Re) | Bestemmelse av friksjonsfaktor |
|---|---|---|
| Laminær strømning | Re < 2000 | λ = 64/Re |
| Overgangsstrøm | 2000 < Re < 4000 | Upålitelig - unngå å designe i dette området |
| Turbulent strømning | Re > 4000 | Bruk oppslagstabeller basert på relativ ruhet (ε/D) |
Praktisk oppslagstabell for friksjonsfaktor
For turbulent strømning i pneumatiske systemer kan du bruke denne forenklede tabellen:
| Rørmateriale | Relativ ruhet (ε/D) | Friksjonsfaktor (λ) ved vanlige Reynolds-tall |
|---|---|---|
| Re = 10 000 | ||
| Glatte slanger (PVC, polyuretan) | 0.0001 – 0.0005 | 0.031 |
| Aluminiumsrør | 0.001 – 0.002 | 0.035 |
| Galvanisert stål | 0.003 – 0.005 | 0.042 |
| Rustent stål | 0.01 – 0.05 | 0.054 |
Beregning av trykkfall i virkelige pneumatiske systemer
La oss gå gjennom et praktisk eksempel:
| Parameter | Verdi/beregning | Eksempel |
|---|---|---|
| Rørdiameter (D) | Innvendig diameter | 8 mm (0,008 m) |
| Rørlengde (L) | Total rett lengde | 5m |
| Strømningshastighet (Q) | Fra systemkrav | 20 standard liter/sekund |
| Luftens tetthet (ρ) | Ved driftstrykk | 7,2 kg/m³ ved 6 bar |
| Strømningshastighet (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Reynolds tall (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1 273 600 |
| Relativ ruhet | For polyuretanslanger | 0.0003 |
| Friksjonsfaktor (λ) | Fra oppslagstabellen | 0.017 |
| Trykkfall (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Anvendelse i den virkelige verden: Løsning av problemer med sylinderhastighet
I fjor jobbet jeg sammen med Sarah, en produksjonsingeniør i et selskap som produserer emballasjeutstyr i Wisconsin. Det stangløse sylindersystemet hennes fungerte bare med 60% av forventet hastighet, til tross for at sylinderen hadde riktig størrelse og tilstrekkelig forsyningstrykk.
Etter å ha analysert systemet hennes, oppdaget jeg at hun brukte 6 mm slanger til en høystrømsapplikasjon. Friksjonstapene førte til et trykkfall på 2,1 bar, noe som reduserte den tilgjengelige kraften og hastigheten betydelig. Ved å oppgradere til 10 mm slanger reduserte vi trykkfallet til 0,4 bar, og systemet hennes oppnådde umiddelbart den nødvendige ytelsen uten noen andre endringer.
Faktorer som påvirker friksjonstap i virkelige systemer
Flere faktorer påvirker det faktiske friksjonstapet:
- Lufttemperatur: Høyere temperaturer øker viskositeten og friksjonen
- Forurensning: Smuss og olje kan øke den effektive ruheten
- Bøying av rør: Mikrodeformasjon i bøyde rør øker motstanden
- Aldersforringelse: Korrosjon og avleiringer øker ruheten over tid
- Driftstrykk: Høyere trykk øker tettheten og tapene
Hvorfor er metoden for ekvivalent lengde avgjørende for nøyaktig systemdesign?
Lokale tap ved rørdeler, ventiler og bend overstiger ofte friksjonstapene i rette rør, men mange ingeniører enten ignorerer dem eller bruker grove estimeringsmetoder som fører til problemer med ytelsen.
Metoden for ekvivalent lengde omregner lokale tap fra armaturer og ventiler til en ekvivalent lengde på et rett rør som vil forårsake samme trykkfall. Dette beregnes ved hjelp av Le = K(D/λ), der Le er den ekvivalente lengden, K er lokal tapskoeffisient4D er rørdiameteren, og λ er friksjonsfaktoren. Denne metoden forenkler beregningene og gir mer nøyaktige prognoser for systemets ytelse.
La oss se nærmere på hvordan denne metoden kan brukes effektivt i design av pneumatiske systemer.
Ekvivalenstabeller for ekvivalent lengde for vanlige pneumatiske komponenter
Her er en praktisk referansetabell for vanlige pneumatiske komponenter:
| Komponent | K-verdi | Ekvivalent lengde (Le/D) |
|---|---|---|
| 90° albue (skarp) | 0.9 | 30 |
| 90° albue (standard radius) | 0.3 | 10 |
| 45° albue | 0.2 | 7 |
| T-kryss (gjennomstrømning) | 0.3 | 10 |
| T-kryss (grenstrøm) | 1.0 | 33 |
| Kuleventil (helt åpen) | 0.1 | 3 |
| Portventil (helt åpen) | 0.2 | 7 |
| Hurtigkobling | 0.4-0.8 | 13-27 |
| Tilbakeslagsventil | 1.5-2.5 | 50-83 |
| Standard strømningsreguleringsventil | 1.0-3.0 | 33-100 |
Bruke metoden for ekvivalent lengde
For å bruke denne metoden effektivt:
- Identifiser alle komponentene i den pneumatiske kretsen
- Finn K-verdien eller det ekvivalente lengdeforholdet (Le/D) for hver komponent
- Beregn ekvivalent lengde ved å multiplisere med rørdiameteren
- Legg alle ekvivalente lengder til den faktiske lengden på det rette røret
- Bruk den totale effektive lengden i beregningene av friksjonstap
For eksempel et system med 5 m rett 8 mm slange pluss fire 90° bend, en T-kobling og to hurtigkoblinger:
| Komponent | Antall | Le/D | Ekvivalent lengde |
|---|---|---|---|
| 90 graders albuer | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| T-kryss | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Hurtigkoblinger | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Total ekvivalent lengde | 0.72m | ||
| Faktisk rett lengde | 5.00m | ||
| Total effektiv lengde | 5.72m |
Dette betyr at systemet på 5 m faktisk oppfører seg som et system på 5,72 m på grunn av lokale tap - en økning på 14,4% i effektiv lengde.
Casestudie: Optimalisering av ventilplassering i monteringssystemer
Jeg hjalp nylig Miguel, en automatiseringsingeniør ved en elektronikkfabrikk i Arizona. Pick-and-place-systemet hans opplevde inkonsekvente bevegelser og variasjoner i syklustid, til tross for at det ble brukt komponenter av høy kvalitet.
Analysen viste at ventilmanifolden var plassert 3 m fra sylindrene, og at kretsen inneholdt en rekke koblinger. Beregningen av ekvivalent lengde viste at den faktiske avstanden på 3 m hadde en effektiv lengde på 7,2 m på grunn av lokale tap - mer enn det dobbelte av avstanden med rett rør!
Ved å flytte ventilmanifolden nærmere sylindrene og eliminere flere beslag, reduserte vi den effektive lengden fra 7,2 m til 2,1 m. Dette reduserte trykkfallet med 70%, noe som resulterte i jevn bevegelse og en reduksjon i syklustiden på 15%.
Praktiske tips for å minimere lokale tap
For å redusere lokale tap i de pneumatiske systemene dine:
- Bruk sveipede eller avrundede albuer i stedet for skarpe bøyer (reduserer K-verdien med 67%)
- Minimer antall beslag ved å planlegge mer direkte ruting
- Velg komponenter med lav restriksjon som fullborede kuleventiler der det er hensiktsmessig
- Riktig størrelse på beslagene - underdimensjonerte beslag forårsaker uforholdsmessig store tap
- Plasser ventiler nær aktuatorene for å minimere effektiv slangelengde
Hva skjer når luft strømmer gjennom reduserte boreseksjoner?
Reduserte boringer i pneumatiske kretser - for eksempel delvis lukkede ventiler, underdimensjonerte beslag eller diameteroverganger - skaper betydelige strømningsbegrensninger som kan påvirke systemets ytelse i alvorlig grad.
Når luft strømmer gjennom reduserte boreseksjoner, trykkfall5 oppstår i henhold til formelen ΔP = ρ(v₂² - v₁²)/2, der v₁ er hastigheten før innsnevringen og v₂ er hastigheten i innsnevringen. Dette kan kompenseres for ved hjelp av kompensasjonsfaktoren C = (1 - (d/D)⁴), der d er den reduserte diameteren og D er den opprinnelige diameteren. Denne faktoren bidrar til å forutsi den faktiske systemytelsen og unngå underdimensjonering av komponenter.
La oss se nærmere på de praktiske konsekvensene av reduserte boreseksjoner og hvordan vi kan ta hensyn til dem i systemdesignet.
Beregning av trykkfall ved diameteroverganger
Når luft strømmer fra en større diameter til en mindre, kan trykkfallet beregnes ved hjelp av :
| Parameter | Formel | Eksempel |
|---|---|---|
| Opprinnelig diameter (D) | Fra spesifikasjoner | 10 mm |
| Redusert diameter (d) | Fra spesifikasjoner | 6 mm |
| Boreforhold (d/D) | Enkel inndeling | 0.6 |
| Strømningshastighet (Q) | Fra systemkrav | 15 standard liter/sekund |
| Hastighet i det opprinnelige røret (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Hastighet i redusert seksjon (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Trykkfall (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Kompensasjonsfaktor (C) | C = (1 - (d/D)⁴) | 0.87 |
Vanlige scenarier for reduksjon av borehull og konsekvensene av disse
Slik påvirker ulike boringsreduksjoner gjennomstrømningskapasiteten:
| Reduksjon av boring | Reduksjon av strømningskapasitet | Økning i trykkfall |
|---|---|---|
| 10 mm til 8 mm | 36% | 2.4× |
| 10 mm til 6 mm | 64% | 7.7× |
| 10 mm til 4 mm | 84% | 39× |
| 8 mm til 6 mm | 44% | 3.2× |
| 8 mm til 4 mm | 75% | 16× |
| 6 mm til 4 mm | 56% | 5.1× |
Disse tallene viser hvorfor tilsynelatende små reduksjoner i diameter kan ha dramatiske effekter på systemytelsen.
Den kumulative effekten av flere restriksjoner
I virkelige pneumatiske kretser forekommer flere restriksjoner i serie. Effekten av disse er kumulativ og kan beregnes ved hjelp av:
- Konverter hver restriksjon til en tilsvarende C-faktor
- Beregn den totale C-faktoren: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Bruk denne totale faktoren til å bestemme den totale ytelsesreduksjonen i systemet
Casestudie: Løsning av problemer med uoverensstemmelser mellom ventil og aktuator
I forrige måned jobbet jeg med Thomas, en vedlikeholdsleder ved en møbelprodusent i North Carolina. Hans nye stangløse sylindersystem fungerte med mindre enn halvparten av forventet hastighet, til tross for at han brukte produsentens anbefalte ventilstørrelse.
Undersøkelsen avslørte flere borehullsreduksjoner i kretsen hans:
- 10 mm tilførselsledning til 8 mm ventilåpninger (C₁ = 0,36)
- 8 mm ventilåpninger til 6 mm beslag (C₂ = 0,44)
- 6 mm koblinger til 8 mm sylinderporter med innvendige begrensninger (C₃ = 0,32)
Den totale kompensasjonsfaktoren var Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, noe som betyr at systemet hans mistet 75% av sin teoretiske strømningskapasitet!
Ved å oppgradere til riktig dimensjonerte komponenter i hele systemet eliminerte vi disse begrensningene og oppnådde den nødvendige ytelsen uten å endre sylinderen eller forsyningstrykket.
Praktiske strategier for å minimere tap ved boringsreduksjon
For å redusere tap fra borehullsreduksjoner:
- Enhetlig størrelse på komponentene gjennom hele den pneumatiske kretsen
- Bruk den største praktiske slangestørrelsen for applikasjoner med høy gjennomstrømning
- Vær oppmerksom på interne komponentbegrensninger, ikke bare tilkoblingsstørrelser
- Vurder parallelle strømningsveier for krav til høy gjennomstrømning
- Eliminer unødvendige adaptere og overganger så langt det er mulig
Prinsippet om "det svakeste leddet" i pneumatiske systemer
Husk at det pneumatiske systemets ytelse begrenses av den mest restriktive komponenten. Et enkelt underdimensjonert element kan oppheve fordelene med riktig dimensjonerte komponenter andre steder i systemet.
For eksempel vil et system med 10 mm slanger, 10 mm ventiler, men 6 mm beslag på sylinderen, i hovedsak ha samme ytelse som et system med 6 mm komponenter gjennomgående - men til en høyere pris.
Konklusjon
Å forstå og beregne strømningsmotstand på riktig måte - ved hjelp av friksjonsfaktortabeller, metoder for ekvivalent lengde og kompensasjon for redusert boring - er avgjørende for å kunne designe pneumatiske systemer som fungerer som forventet under virkelige forhold. Ved å bruke disse beregningsmetodene og designprinsippene kan du optimalisere stangløse sylinderapplikasjoner og andre pneumatiske systemer for å oppnå maksimal ytelse og pålitelighet.
Vanlige spørsmål om strømningsmotstand i pneumatiske systemer
Hvor stort trykkfall er akseptabelt i et pneumatisk system?
Det akseptable trykkfallet avhenger av kravene til bruksområdet, men som en generell retningslinje bør du begrense det totale trykkfallet til 10-15% av forsyningstrykket for effektiv drift. For et 6 bar-system betyr dette at det totale trykkfallet må holdes under 0,6-0,9 bar. Kritiske bruksområder kan kreve enda lavere trykkfall på 5-8% for å opprettholde jevn ytelse.
Hva er forholdet mellom rørdiameter og trykkfall?
Trykkfallet er omvendt proporsjonalt med femte potens av diameteren (D⁵) for turbulent strømning i pneumatiske systemer. Dette betyr at en dobling av rørdiameteren reduserer trykkfallet med omtrent 32 ganger. For eksempel kan en økning fra 6 mm til 12 mm slange redusere trykkfallet fra 1,5 bar til bare 0,047 bar under de samme strømningsforholdene.
Hvordan finner jeg riktig slangestørrelse for min pneumatiske applikasjon?
Velg rørstørrelse basert på krav til strømningshastighet og akseptabelt trykkfall. Beregn Reynolds tall og friksjonsfaktor, og bruk deretter Darcy-Weisbach-ligningen til å bestemme trykkfallet for ulike diametre. Velg den minste diameteren som holder trykkfallet innenfor akseptable grenser (vanligvis <10% av forsyningstrykket), samtidig som du tar hensyn til plassbegrensninger og kostnader.
Hva skaper mest begrensning: en 90° albue eller 5 meter rett slange?
En skarp 90°-vinkel skaper vanligvis motstand som tilsvarer 30 rørdiametere med rett rør. For 8 mm rør tilsvarer en skarp vinkel ca. 240 mm (30 × 8 mm) rett rør. Dette betyr at 5 meter rett rør skaper omtrent 21 ganger mer restriksjon enn én enkelt vinkel. Systemer inneholder imidlertid ofte flere bend og koblinger, og den kumulative effekten av disse kan overstige tapene ved bruk av rette rørlengder.
Hvordan påvirker hurtigkoblinger systemets ytelse?
Standard hurtigkoblinger gir vanligvis et lokalt tap som tilsvarer 15-25 rørdiametere med rette rør. Enda viktigere er det at mange hurtigkoblinger har innvendige begrensninger som er mindre enn den nominelle størrelsen. En "10 mm" hurtigkobling kan ha en innvendig begrensning på bare 7-8 mm, noe som gir en boringsreduksjon som kan redusere strømningskapasiteten med 50-70% på dette punktet.
Hvilken innvirkning har delvis lukkede reguleringsventiler på systemets ytelse?
En strømningsreguleringsventil som er stengt til 50% av sitt fulle gjennomstrømningsareal, reduserer ikke bare strømningen med 50% - den reduserer strømningen med ca. 75% på grunn av det ikke-lineære forholdet mellom diameter og strømningskapasitet. Trykkfallet øker i henhold til kvadratet av hastighetsendringen, slik at en halvering av den effektive diameteren øker trykkfallet med omtrent 16 ganger under de samme strømningsforholdene.
-
Gir en detaljert gjennomgang av Darcy-Weisbach-ligningen, en grunnleggende og mye brukt formel i fluiddynamikk for beregning av trykktap på grunn av friksjon i et rør. ↩
-
Gir en klar definisjon av Reynolds tall, en kritisk dimensjonsløs størrelse som brukes til å forutsi strømningsmønstre (laminære eller turbulente) i ulike væskestrømningssituasjoner. ↩
-
Moody-diagrammet, en omfattende graf som plotter Darcy-friksjonsfaktoren mot Reynolds-tall og relativ ruhet, og som er standardverktøyet for ingeniører for å bestemme trykkfall i rør. ↩
-
Forklarer begrepet K-verdi, eller lokal tapskoeffisient, et dimensjonsløst tall som brukes til å karakterisere trykktapet i en rørkobling eller ventil som en del av ekvivalentlengdemetoden. ↩
-
Beskriver fysikken bak trykkfallet som oppstår når en væske passerer gjennom en begrensning (en åpning), basert på prinsippene i kontinuitetsligningen og Bernoullis prinsipp. ↩




