Trykkmålinger forvirrer selv erfarne ingeniører. Jeg har feilsøkt utallige pneumatiske systemer der feil trykkreferanser har forårsaket ytelsesproblemer. Forståelse av absolutt trykk forhindrer kostbare beregningsfeil og systemfeil.
Absolutt trykk (ABS-trykk) måler trykket i forhold til et perfekt vakuum, og inkluderer atmosfærisk trykk i målingen. Det er lik overtrykk pluss atmosfæretrykk (14,7 PSI ved havnivå), noe som gir det sanne totale trykket som virker på pneumatiske komponenter.
I forrige uke hjalp jeg Thomas, en designingeniør fra et nederlandsk produksjonsselskap, med å løse høyderelaterte ytelsesproblemer med sin stangløs pneumatisk sylinder1 system. Beregningene hans fungerte perfekt ved havnivå, men feilet på fjellanlegget deres. Problemet var ikke svikt i utstyret - det var misoppfatninger om absolutt trykk.
Innholdsfortegnelse
- Hva er absolutt trykk, og hvordan skiller det seg fra manometertrykk?
- Hvorfor er absolutt trykk avgjørende for pneumatiske beregninger?
- Hvordan påvirker høyden det absolutte trykket i pneumatiske systemer?
- Hva er de vanligste bruksområdene for absolutt trykk i industrielle miljøer?
- Hvordan konverterer du mellom ulike trykkmålinger?
- Hvilke feil gjør ingeniører når de beregner absolutt trykk?
Hva er absolutt trykk, og hvordan skiller det seg fra manometertrykk?
Absolutt trykk representerer det totale trykket som virker på et system, målt fra et referansepunkt med perfekt vakuum. Denne målingen inkluderer atmosfæriske trykkeffekter som manometertrykket ikke tar hensyn til.
Absolutt trykk er lik overtrykk pluss atmosfærisk trykk. Ved havnivå er atmosfæretrykket 14,7 PSI, så 80 PSIG overtrykk tilsvarer 94,7 PSIA absolutt trykk. Denne forskjellen er avgjørende for nøyaktige beregninger av pneumatiske systemer.

Forståelse av trykkreferansepunkter
Ulike trykkmålinger bruker forskjellige referansepunkter:
| Trykktype | Referansepunkt | Symbol | Typisk rekkevidde |
|---|---|---|---|
| Absolutt | Perfekt vakuum | PSIA | 0 til 1000+ PSIA |
| Måler | Atmosfærisk | PSIG | -14,7 til 1000+ PSIG |
| Differensial | Mellom to punkter | PSID | Variabel |
| Vakuum | Under atmosfærisk | "Hg | 0 til 29,92"Hg |
Grunnleggende om absolutt trykk
Absolutt trykk gir det komplette trykkbildet. Det omfatter både det påførte trykket og det atmosfæriske trykket som omgir systemet.
Det grunnleggende forholdet er:
PSIA = PSIG + atmosfærisk trykk
Ved standard forhold ved havnivå:
PSIA = PSIG + 14,7
Begrensninger i målertrykk
Målinger av manometertrykk tar ikke hensyn til variasjoner i atmosfæretrykket. Dette skaper problemer når atmosfæretrykket endres på grunn av høyde over havet eller værforhold.
Manometertrykk fungerer godt for de fleste industrielle bruksområder fordi atmosfæretrykket forblir relativt konstant på faste steder. Absolutt trykk blir imidlertid kritisk for:
- Beregninger av høydekompensasjon
- Design av vakuumsystem
- Anvendelser av gassloven
- Beregning av strømningshastighet
- Temperaturkompensasjon
Praktiske måleforskjeller
Jeg jobbet nylig med Anna, en prosessingeniør fra en norsk offshoreplattform. De pneumatiske beregningene hennes fungerte perfekt på land, men sviktet da utstyret ble flyttet til sjøbaserte operasjoner.
Problemet var variasjoner i atmosfæretrykket. Værsystemer skapte endringer i atmosfæretrykket på 1-2 PSI, noe som påvirket målerens trykkavlesninger. Ved å gå over til absolutte trykkmålinger eliminerte vi værrelaterte ytelsesvariasjoner.
Visuell forståelse
Tenk på absolutt trykk som å måle fra bunnen av et svømmebasseng (perfekt vakuum) til vannoverflaten (systemtrykk). Manometertrykk måler kun fra normal vannstand (atmosfærisk trykk) til overflaten.
Denne analogien gjør det lettere å forstå hvorfor absolutt trykk gir mer fullstendig informasjon for tekniske beregninger.
Hvorfor er absolutt trykk avgjørende for pneumatiske beregninger?
Absolutt trykk danner grunnlaget for nøyaktige beregninger av pneumatiske systemer. Mange tekniske formler krever absolutte trykkverdier for å gi korrekte resultater.
Absolutt trykk er avgjørende for pneumatiske beregninger fordi gasslover, strømningsligninger og termodynamiske forhold bruker absolutte trykkverdier. Bruk av manometertrykk i disse formlene gir feil resultater, noe som kan føre til systemfeil.
Anvendelser av gassloven
Den idealgassloven2 krever absolutt trykk for nøyaktige beregninger:
PV = nRT
Hvor?
- P = Absolutt trykk
- V = volum
- n = antall mol
- R = Gasskonstant
- T = Absolutt temperatur3
Bruk av manometertrykk i gasslovberegninger gir feil som er proporsjonale med atmosfæretrykket. Ved havnivå gir dette 15% feil i de fleste beregninger.
Beregning av strømningshastighet
Formler for pneumatisk strømningshastighet krever absolutte trykkforhold:
Strømningshastighet ∝ √(P₁² - P₂²)
Der P₁ og P₂ er absolutt trykk oppstrøms og nedstrøms for en restriksjon.
Bruk av manometertrykk i strømningsberegninger kan gi feil som overstiger 20%, noe som kan føre til underdimensjonerte eller overdimensjonerte systemkomponenter.
Beregninger av sylinderkraft
Mens grunnleggende kraftberegninger (F = P × A) fungerer med manometertrykk, krever avanserte bruksområder absolutt trykk:
Kompensasjon for høyde
Krafteffekten endres med høyden på grunn av variasjoner i atmosfæretrykket. Beregninger av absolutt trykk tar hensyn til disse endringene.
Temperaturpåvirkning
Beregninger av gassekspansjon og -kontraksjon krever absolutte trykk- og temperaturverdier for å være nøyaktige.
Kompressorens ytelse
Ved beregning av kompressordimensjonering og ytelse brukes absolutte trykkforhold:
Kompresjonsforhold = P₂(abs) ÷ P₁(abs)
Dette forholdet bestemmer kompressorens trinnkrav og energiforbruk. Bruk av manometertrykk gir feil kompresjonsforhold4.
Eksempel fra den virkelige verden
Jeg hjalp Marcus, en vedlikeholdssjef fra et sveitsisk presisjonsverksted, med å løse problemet med ujevn ytelse på sylindere uten stang. Anlegget hans lå på 3000 meters høyde, der atmosfæretrykket er 13,2 PSI i stedet for 14,7 PSI ved havnivå.
Manometertrykket viste 80 PSIG, men absoluttrykket var bare 93,2 PSIA i stedet for de forventede 94,7 PSIA. Denne forskjellen på 1,5 PSI reduserte sylinderkraften med 1,6%, noe som førte til problemer med posisjoneringsnøyaktigheten i presisjonsapplikasjoner.
Ved å rekalibrere beregningene hans for lokalt atmosfæretrykk, gjenopprettet vi riktig systemytelse.
Vakuumapplikasjoner
Vakuumsystemer krever absolutt trykkmåling fordi overtrykket blir negativt under atmosfærisk trykk:
| Vakuumnivå | Manometer Trykk | Absolutt trykk |
|---|---|---|
| Grovvakuum | -10 PSIG | 4,7 PSIA |
| Medium vakuum | -13 PSIG | 1,7 PSIA |
| Høyt vakuum | -14,5 PSIG | 0,2 PSIA |
| Perfekt vakuum | -14,7 PSIG | 0,0 PSIA |
Hvordan påvirker høyden det absolutte trykket i pneumatiske systemer?
Høyden over havet har en betydelig innvirkning på atmosfæretrykket, noe som påvirker ytelsen til pneumatiske systemer. Ved å forstå disse effektene kan man forebygge ytelsesproblemer i installasjoner i høyden.
Atmosfæretrykket synker med ca. 0,5 PSI per 1000 fot høydeøkning. Denne reduksjonen påvirker beregningene av absolutt trykk og kan redusere den pneumatiske sylinderkraften med 3-4% per 1 000 fot høyde.
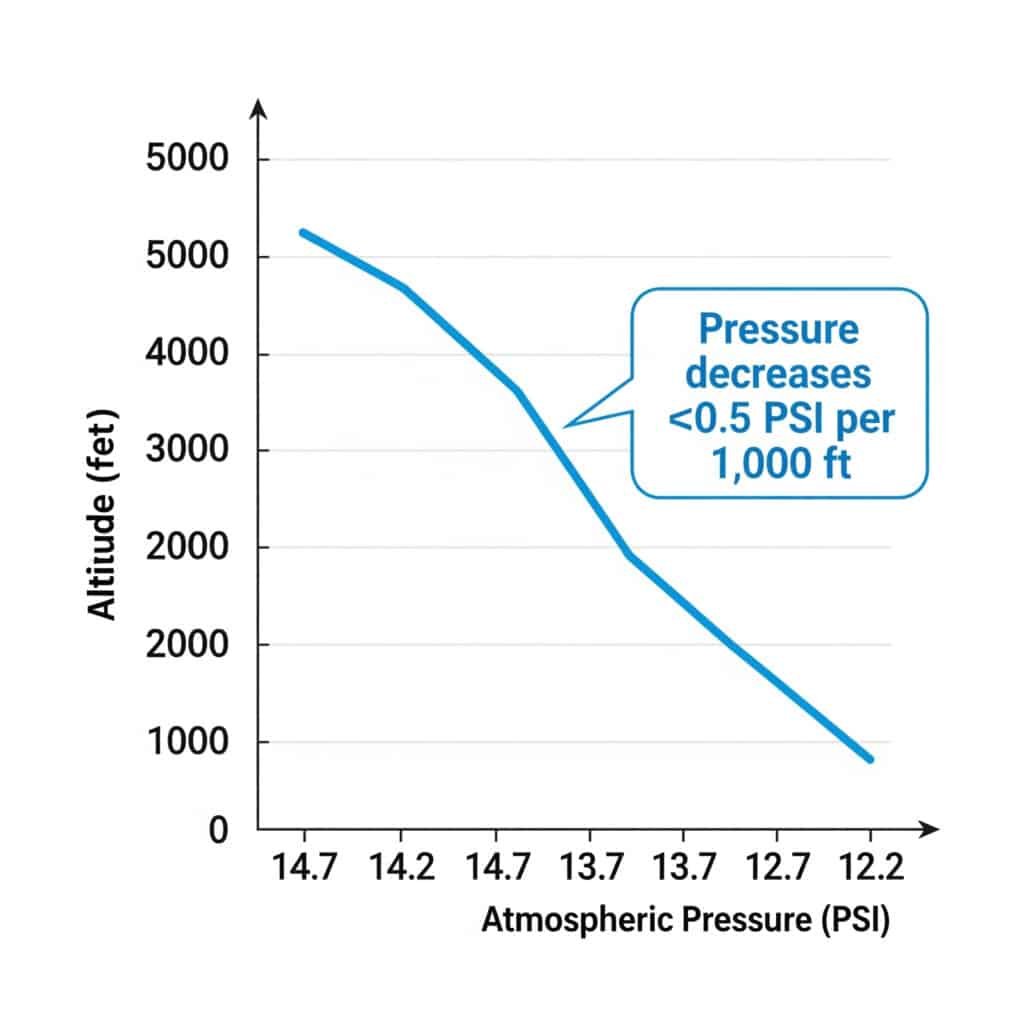
Atmosfærisk trykk vs. høyde over havet
Standard atmosfærisk trykk varierer forutsigbart med høyden:
| Høyde (fot) | Atmosfærisk trykk (PSIA) | Trykkreduksjon |
|---|---|---|
| Havnivå | 14.7 | 0% |
| 1,000 | 14.2 | 3.4% |
| 2,000 | 13.7 | 6.8% |
| 5,000 | 12.2 | 17.0% |
| 10,000 | 10.1 | 31.3% |
Kraftutgang Effekt
Redusert atmosfæretrykk påvirker beregningen av sylinderkraften ved bruk av absolutt trykk:
Effektivt trykk = manometertrykk + lokalt atmosfærisk trykk
For en sylinder som arbeider ved 80 PSIG:
- Havnivå: 80 + 14,7 = 94,7 PSIA
- 5 000 fot: 80 + 12,2 = 92,2 PSIA
- Styrkereduksjon: 2.6%
Strategier for høydekompensasjon
Det finnes flere metoder for å kompensere for høydeeffekter:
Justering av trykk
Øk manometertrykket for å opprettholde konstant absolutt trykk:
Nødvendig manometertrykk = Absolutt måltrykk - lokalt atmosfærisk trykk
Ny utforming av systemet
Endre størrelsen på sylindrene for å opprettholde kraften ved redusert absolutt trykk.
Kompensasjon av kontrollsystem
Programmer kontrollsystemer for å justere for lokale variasjoner i atmosfærisk trykk.
Kombinerte effekter av temperatur og høyde
Både høyde og temperatur påvirker lufttettheten og systemets ytelse:
Lufttetthet = (absolutt trykk × molekylvekt) ÷ (gasskonstant × absolutt temperatur)
Høyere høyder har vanligvis lavere temperaturer, noe som delvis oppveier effekten av trykkreduksjon på lufttettheten.
Høydeapplikasjoner i den virkelige verden
Jeg jobbet sammen med Carlos, en prosjektleder som installerte pneumatiske systemer i en gruvedrift i Peru, på 12 000 meters høyde. Beregningene hans viste at det var tilstrekkelig kraft for materialhåndtering på havnivå.
I installasjonshøyde var det atmosfæriske trykket bare 9,3 PSIA, sammenlignet med 14,7 PSIA ved havnivå. Denne reduksjonen i atmosfærisk trykk på 37% påvirket systemets ytelse betydelig.
Vi kompenserte med:
- Økning av driftstrykket fra 80 til 95 PSIG
- Oppdimensjonering av kritiske sylindere med 15%
- Legge til trykkforsterkere for bruksområder med høy kraft
Det modifiserte systemet leverte ønsket ytelse til tross for ekstreme høydeforhold.
Værpåvirkning i høyden
På steder i stor høyde er det større variasjoner i atmosfæretrykket på grunn av været:
Variasjoner i havnivået
- Høyt trykk: 15,2 PSIA (+0,5 PSI)
- Lavt trykk: 14,2 PSIA (-0,5 PSI)
- Totalt utvalg: 1,0 PSI
Variasjoner i stor høyde (10 000 fot)
- Høyt trykk: 10,6 PSIA (+0,5 PSI)
- Lavt trykk: 9,6 PSIA (-0,5 PSI)
- Totalt utvalg: 1,0 PSI (10% av basistrykket)
Hva er de vanligste bruksområdene for absolutt trykk i industrielle miljøer?
Absolutte trykkmålinger er avgjørende i en rekke industrielle applikasjoner der nøyaktige trykkforhold er avgjørende for systemets ytelse og sikkerhet.
Vanlige bruksområder for absolutt trykk omfatter vakuumsystemer, beregning av gasstrøm, kompressordimensjonering, høydekompensering og termodynamiske prosesser. Disse bruksområdene krever absolutt trykk fordi manometertrykkmålinger gir ufullstendig informasjon.
Design av vakuumsystem
Vakuumapplikasjoner krever absolutte trykkmålinger fordi manometertrykket blir negativt under atmosfæriske forhold:
Dimensjonering av vakuumpumper
Vakuumpumpens kapasitet avhenger av det absolutte trykkforholdet:
Pumpehastighet = Volumstrøm ÷ (P₁ - P₂)
Der P₁ og P₂ er absolutt trykk ved pumpens innløp og utløp.
Spesifikasjoner for vakuumnivå
Industrielle vakuumnivåer bruker absolutt trykkmålinger:
| Søknad | Vakuumnivå (PSIA) | Typisk bruk |
|---|---|---|
| Materialhåndtering | 10-12 | Sugekopper, transportbånd |
| Emballasje | 5-8 | Vakuumpakking |
| Prosessindustrien | 1-3 | Destillasjon, tørking |
| Laboratoriet | 0.1-0.5 | Forskningsapplikasjoner |
Måling av gassgjennomstrømning
Nøyaktige beregninger av gasstrømmen krever absolutte trykkverdier:
Kvelte strømningsforhold
Gasstrømmen blir strupet når trykket nedstrøms faller under kritisk trykk:
Kritisk trykkforhold = 0,528 (for luft)
Denne beregningen krever absolutte trykk for å bestemme strømningsbegrensninger.
Beregning av massestrøm
Massestrømningshastigheten avhenger av absolutt trykk og temperatur:
Massestrøm = (absolutt trykk × areal × hastighet) ÷ (gasskonstant × absolutt temperatur)
Bruksområder for kompressorer
Kompressordimensjonering og -ytelse bruker absolutte trykkforhold:
Beregning av kompresjonsforhold
Kompresjonsforhold = Utløpstrykk (abs) ÷ innsugstrykk (abs)
Dette forholdet avgjør:
- Antall kompresjonstrinn som kreves
- Strømforbruk
- Utløpstemperatur
- Effektivitetsegenskaper
Kart over kompressorens ytelse
Produsentens ytelseskart bruker absolutte trykkforhold for nøyaktig valg og drift.
Applikasjoner for prosesskontroll
Mange prosesskontrollsystemer krever absolutte trykkmålinger:
Beregninger av tetthet
Beregning av gasstetthet for strømningsmåling og -kontroll:
Tetthet = (absolutt trykk × molekylvekt) ÷ (gasskonstant × absolutt temperatur)
Beregninger av varmeoverføring
Termodynamiske beregninger for varmevekslere og prosessutstyr bruker absolutte trykk- og temperaturverdier.
Prosessanvendelse i den virkelige verden
Jeg hjalp nylig Elena, en prosessingeniør ved et tysk kjemisk anlegg, med pneumatisk transport5 systemdesign. Systemet hennes transporterte plastpellets ved hjelp av trykkluft gjennom opphøyde rørledninger.
Transportberegningene krevde absolutte trykkverdier for å bestemme:
- Lufttetthet ved ulike rørledningshøyder
- Beregning av trykkfall gjennom vertikale seksjoner
- Krav til materialhastighet
- Begrensninger i systemkapasiteten
Bruk av manometertrykk ville ha ført til 15-20% feil i beregningene av transportkapasiteten, noe som ville ha ført til underdimensjonert utstyr og dårlig ytelse.
Applikasjoner for kvalitetskontroll
Presisjonsproduksjon krever ofte absolutte trykkmålinger:
Lekkasjetesting
Absolutte trykkmålinger gir mer nøyaktig lekkasjedeteksjon:
Lekkasjehastighet = volum × trykkfall ÷ tid
Ved å bruke absolutt trykk eliminerer man atmosfæriske trykkvariasjoner som påvirker manometeravlesningene.
Kalibreringsstandarder
Trykkalibreringsstandarder bruker absolutte trykkreferanser for nøyaktighet og sporbarhet.
Hvordan konverterer du mellom ulike trykkmålinger?
Trykkomregning mellom ulike målesystemer krever forståelse av referansepunkter og omregningsfaktorer. Nøyaktige omregninger forhindrer beregningsfeil i internasjonale prosjekter.
Trykkomregninger krever at man legger til eller trekker fra atmosfærisk trykk når man veksler mellom absolutte målinger og manometermålinger, i tillegg til å bruke enhetsomregningsfaktorer. Vanlige omregninger inkluderer PSIA til bar, PSIG til kPa og vakuummålinger til absolutt trykk.
Grunnleggende konverteringsformler
Det grunnleggende forholdet mellom trykktyper:
Absolutt trykk = manometertrykk + atmosfærisk trykk
Manometertrykk = absolutt trykk - atmosfærisk trykk
Vakuum = atmosfærisk trykk - absolutt trykk
Omregningsfaktorer for enheter
Omregning av vanlige trykkenheter:
| Fra | Til | Multipliser med | | Multipliser med
|——|—-|———–|
| PSI | bar | 0,06895
| bar | PSI | 14.504 | 14.504
| PSI | kPa | 6,895
| kPa | PSI | 0,1450 | 0,1450
| PSI | "Hg | 2,036 |
| "Hg | PSI | 0,4912 |
Standarder for atmosfærisk trykk
Standardverdier for atmosfærisk trykk for omregninger:
| Beliggenhet/Standard | Trykkverdi |
|---|---|
| Havnivåstandard | 14,696 PSIA, 1,01325 bar |
| Teknisk standard | 14,7 PSIA, 1,013 bar |
| Metrisk standard | 101,325 kPa, 760 mmHg |
Eksempler på konvertering
Konvertering fra PSIG til PSIA
80 PSIG til PSIA ved havnivå:
80 PSIG + 14,7 = 94,7 PSIA
Bar Gauge til Bar Absolutt
5 barg til bara ved havnivå:
5 barg + 1,013 = 6,013 bara
Vakuum til absolutt trykk
25"Hg vakuum til PSIA:
14,7 - (25 × 0,4912) = 2,42 PSIA
Hensyn til internasjonale enheter
Ulike land bruker forskjellige trykkenheter:
| Region | Felles enheter | Standard Atmosfærisk |
|---|---|---|
| USA | PSIG, PSIA | 14,7 PSI |
| Europa | bar, kPa | 1,013 bar |
| Asia | MPa, kgf/cm² | 1,033 kgf/cm² |
| Vitenskapelig | Pa, kPa | 101,325 kPa |
Betraktninger rundt konverteringsnøyaktighet
Omregningsnøyaktigheten avhenger av antagelser om atmosfærisk trykk:
Standard vs. faktiske forhold
- Standard: Bruker 14,7 PSI atmosfærisk trykk
- Faktisk: Bruker lokalt atmosfærisk trykk
- Feil: Kan være 1-3% avhengig av sted og værforhold
Temperaturpåvirkning
Atmosfæretrykket varierer med temperatur og værforhold. For presise omregninger bør du bruke det faktiske lokale atmosfæretrykket i stedet for standardverdier.
Digitale konverteringsverktøy
Moderne trykkinstrumenter tilbyr ofte automatisk enhetskonvertering. Men ved å forstå prinsippene for manuell omregning er det lettere å verifisere digitale målinger og feilsøke konverteringsfeil.
Praktisk anvendelse av konvertering
Jeg samarbeidet med Jean-Pierre, en prosjektingeniør fra en fransk bilprodusent, om spesifikasjonene for et pneumatisk system i et globalt prosjekt. De europeiske spesifikasjonene hans brukte bar overtrykk, men den nordamerikanske installasjonen krevde PSIG-verdier.
Konverteringsprosessen involvert:
- Europeisk spesifikasjon: 6 barg driftstrykk
- Konverter til absolutt: 6 + 1,013 = 7,013 bara
- Konverter enheter: 7,013 × 14,504 = 101,7 PSIA
- Konverter til Gauge: 101,7 - 14,7 = 87,0 PSIG
Denne systematiske tilnærmingen sikret nøyaktige trykkspesifikasjoner på tvers av ulike målesystemer og forhindret feil i utstyrsdimensjoneringen.
Hvilke feil gjør ingeniører når de beregner absolutt trykk?
Feil i beregningen av absolutt trykk er vanlige og kan føre til betydelige problemer med systemytelsen. Ved å forstå disse feilene kan du forebygge kostbare konstruksjons- og driftsproblemer.
Vanlige feil ved absolutt trykk omfatter bruk av manometertrykk i gasslovberegninger, ignorering av atmosfæriske trykkvariasjoner, feilaktig enhetskonvertering og misforståelse av vakuummålinger. Disse feilene fører vanligvis til unøyaktigheter i 10-30%-beregningene og problemer med systemytelsen.
Bruk av manometertrykk i gasslovberegninger
Den vanligste feilen er å bruke manometertrykk i formler som krever absolutt trykk:
Feil anvendelse av gassloven
Feil: PV = nRT ved bruk av manometertrykk
Riktig: PV = nRT ved bruk av absolutt trykk
Denne feilen skaper beregningsfeil som er proporsjonal med atmosfæretrykket - ca. 15% ved havnivå.
Ignorerer variasjoner i atmosfærisk trykk
Mange ingeniører antar et konstant atmosfærisk trykk på 14,7 PSI, uavhengig av sted eller forhold:
Variasjoner i beliggenhet
- Havnivå: 14,7 PSIA
- Denver (5 280 fot): 12,2 PSIA
- Feil: 17% hvis du bruker verdien for havnivå i Denver
Variasjoner i været
- Høytrykkssystem: 15,2 PSIA
- Lavtrykkssystem: 14,2 PSIA
- Variasjon: ±3,4% fra standard
Feilaktig omregning av enheter
Blanding av absolutte og manometriske trykkenheter skaper betydelige feil:
Vanlige konverteringsfeil
- Legger til 14,7 til barmåleravlesninger (skal legge til 1,013)
- Bruk av 14,7 PSI for steder som ikke ligger på havnivå
- Glemmer å konvertere mellom absolutt og måleenhet når du bytter enhet
Forvirring rundt vakuummålinger
Vakuummålinger forvirrer ofte ingeniører fordi de representerer trykk under atmosfærisk trykk:
Forhold mellom vakuum og trykk
- 29 "Hg Vakuum = 0,76 PSIA (ikke -29 PSIA)
- Perfekt vakuum = 0 PSIA absolutt
- Atmosfærisk trykk = Maksimalt mulig vakuum i "Hg
Jeg hjalp nylig Roberto, en designingeniør fra et italiensk emballasjeselskap, med å løse problemer med vakuumsystemets ytelse. Beregningene hans viste at vakuumpumpekapasiteten var tilstrekkelig, men systemet klarte ikke å oppnå de nødvendige vakuumnivåene.
Problemet var forvirring rundt vakuummålingen. Roberto beregnet pumpebehovet ved hjelp av -25 PSIG i stedet for det korrekte absolutte trykket på 1,4 PSIA. Denne feilen fikk pumpen til å virke 18 ganger kraftigere enn den faktiske kapasiteten.
Temperaturkompensasjonsfeil
Beregninger av absolutt trykk tar ofte ikke hensyn til temperatureffekter:
Temperaturkrav i gassloven
Gasslovberegninger krever absolutt temperatur (Rankine eller Kelvin):
- Fahrenheit til Rankine: °R = °F + 459,67
- Celsius til Kelvin: K = °C + 273,15
Bruk av Fahrenheit- eller Celsius-temperaturer i gasslovberegninger gir betydelige feil.
Overvåking av høydekompensasjon
Ingeniører bruker ofte atmosfærisk trykk på havnivå for installasjoner i stor høyde:
Trykkfeil i høyden
På 3000 meters høyde:
- Faktisk atmosfærisk: 10.1 PSIA
- Antagelse om havnivå: 14,7 PSIA
- Feil: 45% overestimering av absolutt trykk
Feil ved beregning av kompressorforhold
Beregninger av kompresjonsforhold krever absolutt trykk, men ingeniører bruker ofte manometertrykk:
Feil kompresjonsforhold
For 80 PSIG utløp, atmosfærisk sug:
- Feil: 80 ÷ 0 = udefinert
- Riktig: 94.7 ÷ 14.7 = 6.44:1
Feil i strømningsberegningen
Beregning av strømningshastighet ved hjelp av trykkdifferanser krever absolutte trykkverdier:
Feil ved kvalt strømning
Beregninger av kritisk trykkforhold:
- Feil: Bruk av manometertrykkforhold
- Riktig: Bruk av absolutte trykkforhold
- Påvirkning: Kan overestimere strømningskapasiteten med 15-20%
Feil i utformingen av sikkerhetssystemer
Dimensjonering av sikkerhetsventilen krever beregning av absolutt trykk:
Dimensjonering av overtrykksventil
Avlastningsventilens kapasitet avhenger av absolutte trykkforhold. Bruk av manometertrykk kan resultere i underdimensjonerte overtrykksventiler og sikkerhetsrisikoer.
Strategier for forebygging
Unngå feil ved beregning av absolutt trykk gjennom:
Systematisk tilnærming
- Identifiser ønsket trykktype: Avgjør om beregningen krever absolutt trykk eller manometertrykk
- Bruk riktig atmosfærisk trykk: Bruk lokalt atmosfærisk trykk, ikke standard havnivå
- Verifiser enhetens konsistens: Sørg for at alle trykk bruker samme enhetssystem
- Dobbeltsjekk konverteringer: Verifiser omregningsfaktorer og referansepunkter
Standarder for dokumentasjon
- Tydelig merking av trykktyper: Angi alltid PSIA, PSIG, bara, barg
- Statlige referansebetingelser: Dokumenter antagelser om atmosfærisk trykk
- Inkluder konverteringstabeller: Oppgi referanseomregningsfaktorer
Konklusjon
Absolutt trykk gir et komplett trykkbilde som er avgjørende for nøyaktige beregninger av pneumatiske systemer. Forståelse av prinsippene for absolutt trykk forhindrer vanlige beregningsfeil og sikrer pålitelig ytelse for stangløse sylindersystemer under varierende driftsforhold.
Vanlige spørsmål om absolutt trykk i pneumatiske systemer
Hva er forskjellen mellom absolutt trykk og manometertrykk?
Absolutt trykk måler det totale trykket fra perfekt vakuum, mens overtrykk måler trykket over atmosfærisk trykk. Absolutt trykk er lik overtrykk pluss atmosfærisk trykk (14,7 PSI ved havnivå).
Hvorfor krever pneumatiske beregninger absolutt trykk?
Gasslover, strømningsligninger og termodynamiske beregninger krever absolutt trykk fordi de involverer trykkforhold og relasjoner som trenger fullstendige trykkverdier. Bruk av manometertrykk gir beregningsfeil på 10-30%.
Hvordan påvirker høyden det absolutte trykket i pneumatiske systemer?
Atmosfæretrykket synker med ca. 0,5 PSI per 1000 fot høyde over havet. Dette reduserer absolutt trykk og kan redusere sylinderkraften med 3-4% per 1000 fot, med mindre det kompenseres gjennom trykkjusteringer.
Hvordan konverterer du manometertrykk til absolutt trykk?
Legg til atmosfærisk trykk til manometertrykket: PSIA = PSIG + atmosfærisk trykk. Bruk lokalt atmosfæretrykk (varierer med høyden) i stedet for standard 14,7 PSI for nøyaktige omregninger.
Hva skjer hvis du bruker overtrykk i beregninger av absolutt trykk?
Bruk av manometertrykk i formler som krever absolutt trykk, skaper feil som er proporsjonale med atmosfæretrykket - vanligvis 15% ved havnivå. Disse feilene kan føre til underdimensjonert utstyr og dårlig systemytelse.
Krever stangløse sylindere beregning av absolutt trykk?
Ja, sylindere uten stang bruker de samme trykkforholdene som tradisjonelle sylindere. Kraftberegninger, strømningsdimensjonering og ytelsesanalyser drar alle nytte av absolutte trykkverdier, spesielt ved bruk i høyden eller under vakuum.
-
Lær mer om design- og driftsfordelene med stangløse pneumatiske sylindere, som ofte brukes til materialhåndtering og automatisering. ↩
-
Utforsk idealgassloven (PV=nRT), en grunnleggende tilstandsligning som beskriver forholdet mellom trykk, volum og temperatur i en gass. ↩
-
Lær om absolutte temperaturskalaer som Kelvin og Rankine, og hvorfor de er viktige for termodynamiske beregninger og gasslovberegninger. ↩
-
Forstå betydningen av kompresjonsforholdet for kompressorens ytelse og hvordan det beregnes ved hjelp av absolutt trykk. ↩
-
Oppdag hvordan pneumatiske transportsystemer fungerer for å transportere bulkmaterialer ved hjelp av komprimert gass i industrielle prosesser. ↩




