Sliter du stadig med beregninger av pneumatiske systemer? Mange ingeniører står overfor det samme problemet når de skal designe eller feilsøke pneumatiske systemer. Den gode nyheten er at du kan løse de fleste pneumatiske utfordringer ved å beherske noen få nøkkelligninger.
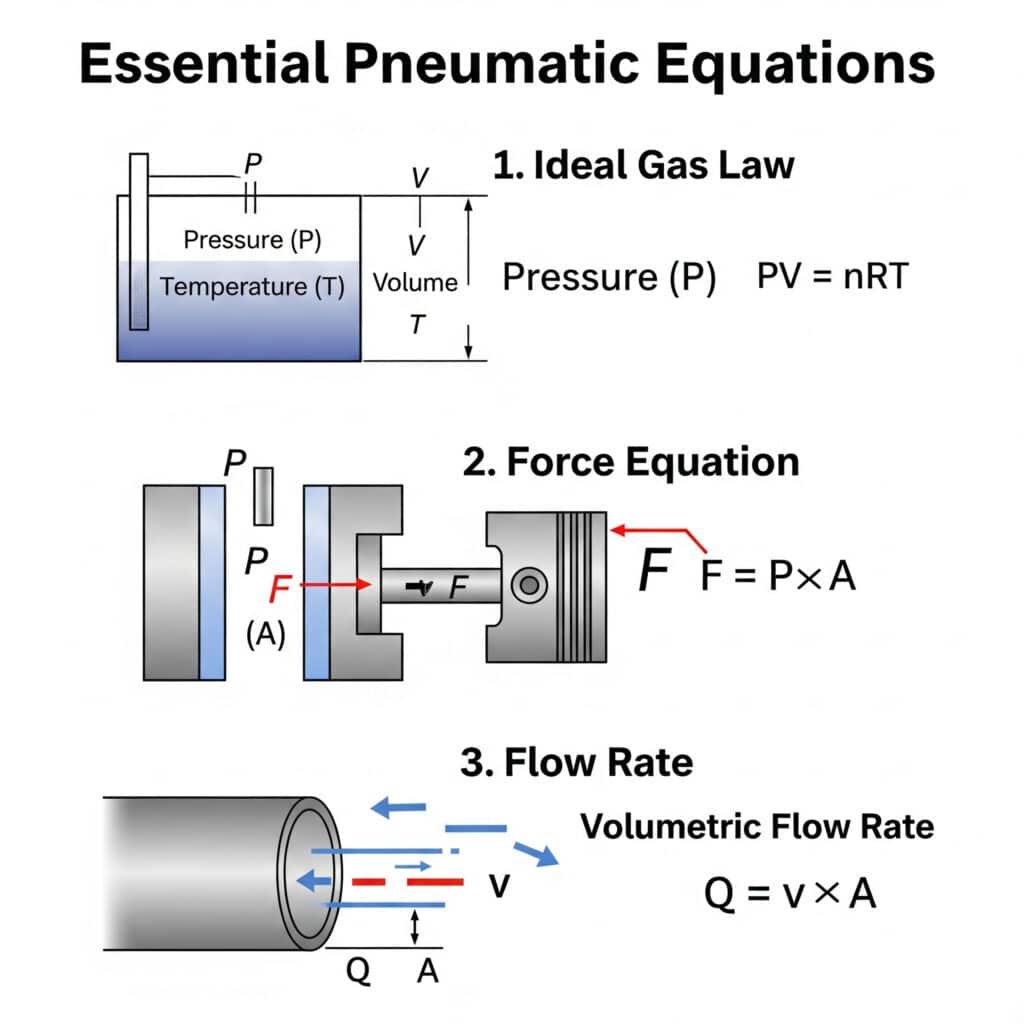
De viktigste ligningene for pneumatisk transmisjon som alle ingeniører bør kjenne til, inkluderer idealgassloven (PV = nRT)1, kraftlikning (F = P × A) og strømningshastighetsforhold (Q = v × A). Forståelse av disse grunnleggende prinsippene gjør det mulig å designe og feilsøke systemet nøyaktig.
Jeg har jobbet med pneumatiske systemer i Bepto i over 15 år, og jeg har sett hvordan forståelse av disse grunnleggende ligningene kan spare tusenvis av kroner i nedetid og forhindre kostbare designfeil.
Innholdsfortegnelse
- Utledning av gassligningen: Hvorfor er PV = nRT viktig i pneumatiske systemer?
- Hvordan henger kraft, trykk og areal sammen i pneumatiske sylindere?
- Hva er forholdet mellom strømningshastighet og hastighet i pneumatiske systemer?
- Konklusjon
- Vanlige spørsmål om ligninger for pneumatisk overføring
Utledning av gassligningen: Hvorfor er PV = nRT viktig i pneumatiske systemer?
Når man designer pneumatiske systemer, er det avgjørende å forstå hvordan gasser oppfører seg under ulike forhold. Denne kunnskapen kan utgjøre forskjellen mellom et system som fungerer pålitelig, og et system som svikter uventet.
Den ideelle gassloven (PV = nRT) er grunnleggende for pneumatiske systemer fordi den beskriver hvordan trykk, volum og temperatur samvirker. Dette forholdet hjelper ingeniører med å forutsi hvordan luft vil oppføre seg i sylindere uten stang og andre pneumatiske komponenter under varierende driftsforhold.

Den ideelle gassloven kan virke som et teoretisk konsept fra fysikkundervisningen, men den har direkte praktisk anvendelse i pneumatiske systemer. La meg forklare dette i mer praktiske termer.
Forstå variablene i PV = nRT
| Variabel | Betydning | Pneumatisk anvendelse |
|---|---|---|
| P | Trykk | Driftstrykket i systemet ditt |
| V | Volum | Størrelse på luftkammer i sylindere |
| n | Antall mol | Mengde luft i systemet |
| R | Gasskonstant2 | Universell konstant (8,314 J/mol-K) |
| T | Temperatur | Driftstemperatur |
Hvordan temperaturen påvirker pneumatisk ytelse
Temperaturvariasjoner kan ha betydelig innvirkning på ytelsen til pneumatiske systemer. I fjor kontaktet en av våre kunder i Tyskland, Hans, meg på grunn av ujevn ytelse i det stangløse sylindersystemet hans. Systemet fungerte perfekt om morgenen, men mistet kraften om ettermiddagen.
Etter å ha analysert oppsettet hans oppdaget vi at systemet var utsatt for direkte sollys, noe som førte til en temperaturøkning på 15 °C. Ved hjelp av idealgassloven beregnet vi at denne temperaturendringen førte til en trykkvariasjon på nesten 5%. Vi installerte riktig isolasjon, og problemet ble løst umiddelbart.
Praktiske anvendelser av gassloven i pneumatisk design
Ved utforming av pneumatiske systemer med stangløse sylinderehjelper gassloven oss:
- Beregn trykkendringer på grunn av temperatursvingninger
- Bestem volumkrav for luftbeholdere
- Forutsi variasjoner i kraftuttaket under ulike forhold
- Kompressorer med riktig størrelse for bruksområdet
Hvordan henger kraft, trykk og areal sammen i pneumatiske sylindere?
Å forstå forholdet mellom kraft, trykk og areal er avgjørende når du skal velge riktig stangløs sylinder til ditt bruksområde. Denne kunnskapen sikrer at du får den ytelsen du trenger uten å bruke for mye penger.
Den forholdet mellom kraft-trykk-areal3 i pneumatiske sylindere defineres av F = P × A, der F er kraft (N), P er trykk (Pa) og A er det effektive arealet (m²). Denne ligningen gjør det mulig for ingeniører å beregne den nøyaktige kraften i sylindere uten stang ved ulike driftstrykk.
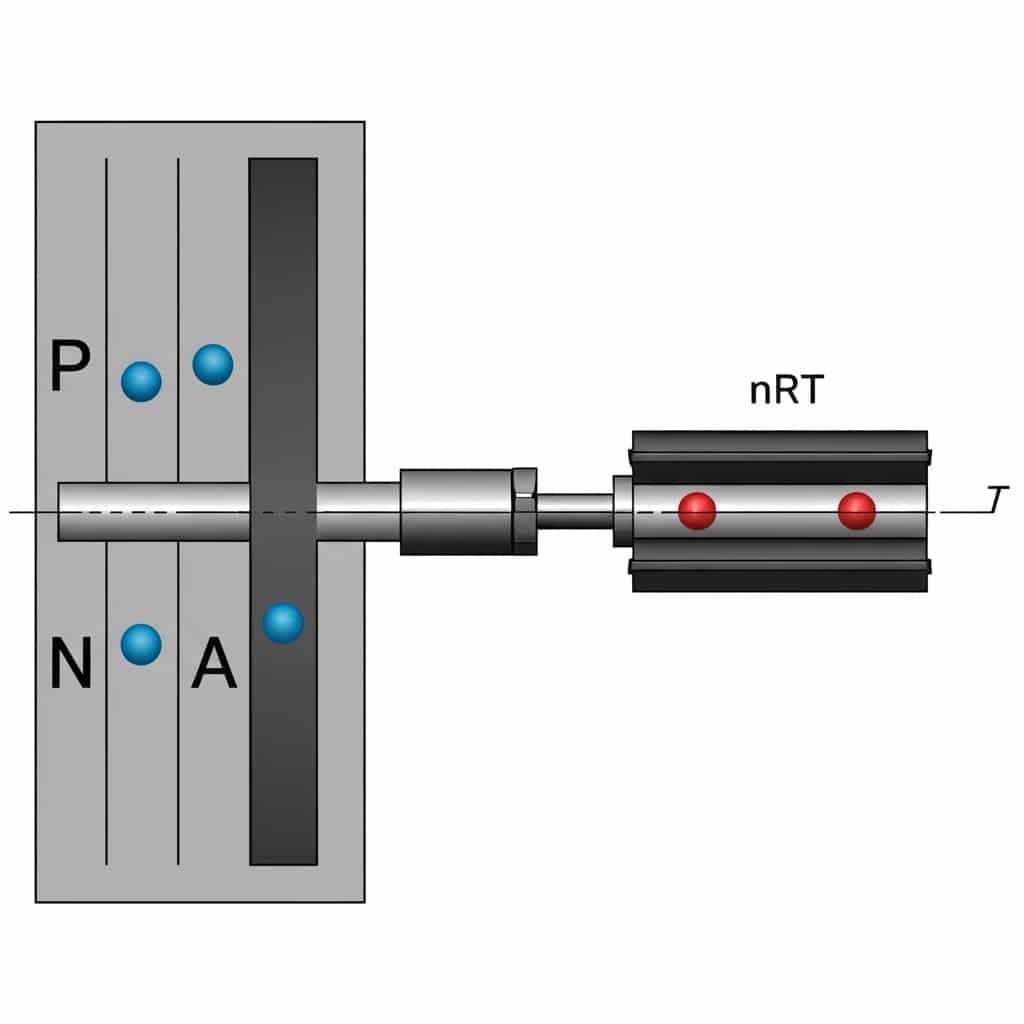
Denne enkle ligningen er grunnlaget for alle pneumatiske kraftberegninger, men det er flere praktiske hensyn som mange ingeniører overser.
Beregning av effektivt areal for ulike flasketyper
Det effektive arealet varierer avhengig av sylindertype:
| Sylindertype | Beregning av effektivt areal | Merknader |
|---|---|---|
| Enkeltvirkende | A = πr² | Fullt boreområde |
| Dobbeltvirkende (forlengelse) | A = πr² | Fullt boreområde |
| Dobbeltvirkende (tilbaketrekking) | A = π(r² - r'²) | r' er stangens radius |
| Sylinder uten stang | A = πr² | Konsekvent i begge retninger |
Effektivitetsfaktorer i den virkelige verden
I praksis påvirkes den faktiske kraften av:
- Friksjonstap: Vanligvis 3-20%, avhengig av tetningsdesign
- Trykkfall: Kan redusere det effektive trykket med 5-10%
- Dynamiske effekter: Akselerasjonskrefter kan redusere tilgjengelig kraft
Jeg husker at jeg jobbet sammen med Sarah, en maskiningeniør fra et emballasjeselskap i Storbritannia. Hun skulle konstruere en ny maskin og hadde regnet ut at hun trengte en stangløs sylinder med en boring på 63 mm for å oppnå den nødvendige kraften. Hun hadde imidlertid ikke tatt høyde for friksjonstap.
Vi anbefalte å gå over til en sylinder med 80 mm boring, noe som ga nok ekstra kraft til å overvinne friksjonen samtidig som den nødvendige ytelsen ble opprettholdt. Denne enkle justeringen sparte henne for en kostbar redesign etter installasjonen.
Sammenligning av teoretisk og faktisk kraftproduksjon
Når du velger sylindere uten stang, anbefaler jeg alltid:
- Beregn teoretisk kraft ved hjelp av F = P × A
- Bruk en sikkerhetsfaktor på 25% for de fleste bruksområder
- Verifiser beregningene med faktiske ytelsesdata fra produsenten
- Vurder dynamiske belastningsforhold hvis det er aktuelt
Hva er forholdet mellom strømningshastighet og hastighet i pneumatiske systemer?
Strømningshastighet og hastighet er kritiske parametere som avgjør hvor raskt det pneumatiske systemet reagerer. Forståelse av dette forholdet bidrar til å forhindre treg ytelse og sikrer at systemet oppfyller kravene til syklustid.
Forholdet mellom strømningshastighet (Q) og hastighet (v)4 i pneumatiske systemer er definert ved Q = v × A, der Q er volumstrømningshastigheten, v er lufthastigheten og A er tverrsnittsarealet i passasjen. Denne ligningen er avgjørende for riktig dimensjonering av luftledninger og ventiler.
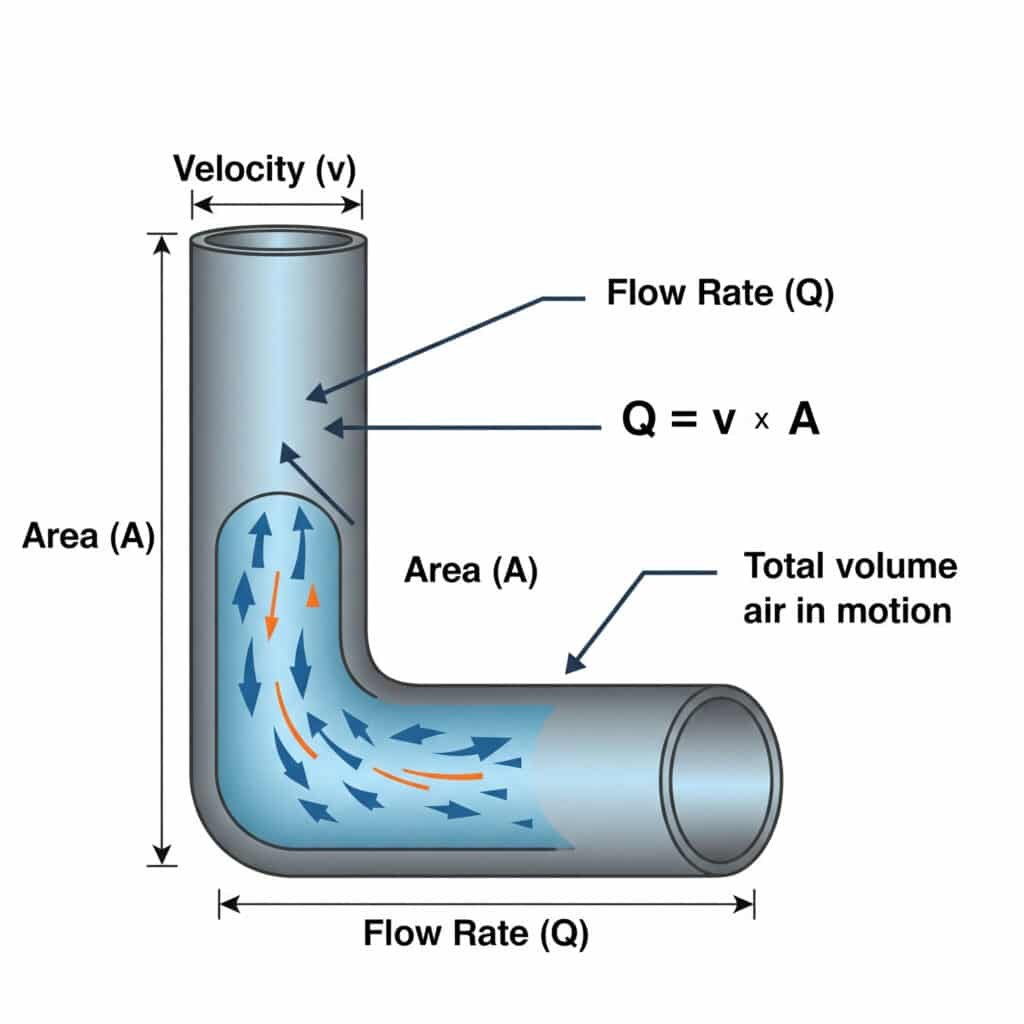
Mange problemer med pneumatiske systemer skyldes feil dimensjonering av lufttilførselskomponenter. La oss se nærmere på hvordan denne ligningen påvirker ytelsen i den virkelige verden.
Kritiske strømningshastigheter for vanlige pneumatiske komponenter
Ulike komponenter har ulike krav til gjennomstrømning:
| Komponent | Typisk krav til strømningshastighet | Konsekvenser av underdimensjonering |
|---|---|---|
| Sylinder uten stang (25 mm boring) | 15-30 l/min | Langsom drift, redusert kraft |
| Stangløs sylinder (63 mm boring) | 60-120 l/min | Inkonsekvent bevegelse |
| Retningsstyrt reguleringsventil | Varierer etter størrelse | Trykkfall, treg respons |
| Enhet for luftforberedelse | System totalt + 30% | Trykksvingninger |
Hvordan rørdiameteren påvirker systemets ytelse
Diameteren på luftledningene har en dramatisk effekt på systemets ytelse:
- Trykkfall: Øker med kvadratet av hastigheten
- Svartid: Mindre linjer betyr høyere hastighet, men mer motstand
- Energieffektivitet: Større ledninger reduserer trykkfallet, men øker kostnadene
Beregning av riktig ledningsstørrelse for pneumatiske systemer
For å dimensjonere luftledningene riktig for din stangløse sylinderapplikasjon:
- Bestem nødvendig gjennomstrømningshastighet basert på sylinderstørrelse og syklustid
- Beregn maksimalt tillatt trykkfall (vanligvis 0,1 bar eller mindre)
- Velg en linediameter som holder hastigheten under 15-20 m/s
- Kontroller ventilens strømningskapasitet (Cv- eller Kv-verdi5) samsvarer med systemkravene
En gang hjalp jeg en kunde i Frankrike som opplevde treg sylinderbevegelse til tross for at han hadde en stor kompressor. Problemet var ikke utilstrekkelig luftgenerering - det var at slangene på 6 mm skapte for mye motstand. En oppgradering til 10 mm rør løste problemet umiddelbart, og økte maskinens syklushastighet med 40%.
Konklusjon
Forståelsen av disse tre grunnleggende pneumatiske ligningene - den ideelle gassloven, forholdet mellom kraft, trykk og areal og sammenhengen mellom strømningshastighet og hastighet - danner grunnlaget for vellykket design av pneumatiske systemer. Ved å bruke disse prinsippene kan du velge de riktige stangløse sylinderkomponentene, feilsøke problemer effektivt og optimalisere systemets ytelse.
Vanlige spørsmål om ligninger for pneumatisk overføring
Hva er idealgassloven, og hvorfor er den viktig for pneumatiske systemer?
Den ideelle gassloven (PV = nRT) beskriver hvordan trykk, volum, temperatur og gassmengde henger sammen i et pneumatisk system. Den er viktig fordi den hjelper ingeniører med å forutsi hvordan endrede forhold (spesielt temperatur) vil påvirke systemets ytelse og trykkbehov.
Hvordan beregner jeg kraften i en sylinder uten stang?
Beregn kraften ved å multiplisere trykket med det effektive arealet (F = P × A). For en sylinder uten stang er det effektive arealet det samme i begge retninger, noe som gjør kraftberegningene enklere enn med konvensjonelle sylindere som har forskjellige ut- og inntrekkskrefter.
Hva er forskjellen mellom strømningshastighet og hastighet i pneumatiske systemer?
Strømningshastighet er volumet av luft som beveger seg gjennom et system per tidsenhet (vanligvis i l/min), mens hastighet er hastigheten som luften beveger seg med gjennom en passasje (i m/s). De er relatert til hverandre ved hjelp av ligningen Q = v × A, der A er tverrsnittsarealet til passasjen.
Hvordan påvirker temperaturen ytelsen til pneumatiske systemer?
Temperaturen påvirker trykket direkte i henhold til den ideelle gassloven. En temperaturøkning på 10 °C kan øke trykket med ca. 3,5% hvis volumet forblir konstant. Dette kan føre til trykkvariasjoner, påvirke tetningenes ytelse og endre kraftutgangen i sylindere uten stang.
Hva er den vanligste årsaken til trykkfall i pneumatiske systemer?
De vanligste årsakene til trykkfall er underdimensjonerte luftledninger, restriktive armaturer og utilstrekkelig ventilstrømningskapasitet. I henhold til strømningshastighetsligningen krever mindre passasjer høyere lufthastighet, noe som øker motstanden og trykkfallet eksponentielt.
Hvordan dimensjonerer jeg luftledninger riktig for en stangløs sylinder?
Dimensjoner luftledningene ved å beregne nødvendig strømningshastighet basert på sylindervolum og syklustid, og velg deretter en ledningsdiameter som holder lufthastigheten under 15-20 m/s for å minimere trykkfallet. For de fleste bruksområder med stangløse sylindere gir 8-12 mm rør en god balanse mellom ytelse og kostnad.
-
Gir en detaljert forklaring av idealgassloven, den grunnleggende tilstandsligningen for en hypotetisk idealgass som gir en tilnærmet beskrivelse av hvordan mange gasser oppfører seg under ulike forhold. ↩
-
Forklarer rollen og verdien til den universelle gasskonstanten (R) i idealgassloven, som fungerer som en fysisk konstant som knytter energiskalaer sammen med temperaturskalaer. ↩
-
Gir en grunnleggende forklaring på trykk, definert som kraften som påføres vinkelrett på overflaten av et objekt per arealenhet som kraften fordeles over. ↩
-
Beskriver prinsippet i kontinuitetsligningen, et grunnleggende konsept innen fluiddynamikk som sier at for en inkompressibel væske må massestrømmen være konstant fra ett tverrsnitt av et rør til et annet. ↩
-
Gir en teknisk definisjon av strømningskoeffisient (Cv) og strømningsfaktor (Kv), som er standardiserte verdier som brukes til å sammenligne strømningskapasiteten til ulike ventiler. ↩


