
Har du noen gang gått inn på fabrikkgulvet og blitt truffet av den umiskjennelige susingen fra pneumatiske systemer? Denne støyen er ikke bare irriterende - den representerer bortkastet energi, potensielle regulatoriske problemer og et advarselstegn på ineffektiv drift.
Akustisk støy i pneumatiske systemer genereres gjennom tre primære mekanismer: gassekspansjon under trykkavlastning, mekanisk vibrasjon i komponenter og turbulent strømning i rør og koblinger. Ved å forstå disse mekanismene kan ingeniører implementere målrettede strategier for støyreduksjon som forbedrer sikkerheten på arbeidsplassen, øker energieffektiviteten og forlenger utstyrets levetid.
I forrige måned besøkte jeg et farmasøytisk produksjonsanlegg i New Jersey, hvor støyen fra deres stangløse sylindere skapte regulatoriske bekymringer. Teamet deres hadde prøvd generiske løsninger uten å lykkes. Ved å analysere de spesifikke støygenereringsmekanismene reduserte vi systemstøyen med 14 dBA - fra å utgjøre en risiko for regelverket til å være godt innenfor kravene. La meg vise deg hvordan vi gjorde det.
Innholdsfortegnelse
- Lydnivå ved gassekspansjon: Hvilken formel forutsier pneumatisk eksosstøy?
- Mekanisk vibrasjonsspektrum: Hvordan kan frekvensanalyse identifisere støykilder?
- Innsettingstap i lyddempere: Hvilke beregninger ligger til grunn for effektiv lyddemperdesign?
- Konklusjon
- Vanlige spørsmål om støy fra pneumatiske systemer
Lydnivå ved gassekspansjon: Hvilken formel forutsier pneumatisk eksosstøy?
Den plutselige ekspansjonen av trykkluft under ventildrift eller sylinderutblåsning er en av de viktigste støykildene i pneumatiske systemer. For å kunne redusere støyen effektivt er det avgjørende å forstå det matematiske forholdet mellom systemparametere og støyutgang.
Lydeffektnivået fra gassekspansjon kan beregnes ved hjelp av formelen: Lw = 10 log₁₀(W/W₀), der W er den akustiske effekten i watt og W₀ er referanseeffekten (10-¹² watt). For pneumatiske systemer kan W beregnes som W = η × m × (c²/2), der η er den akustiske virkningsgraden, m er massestrømningshastigheten og c er gasshastigheten.
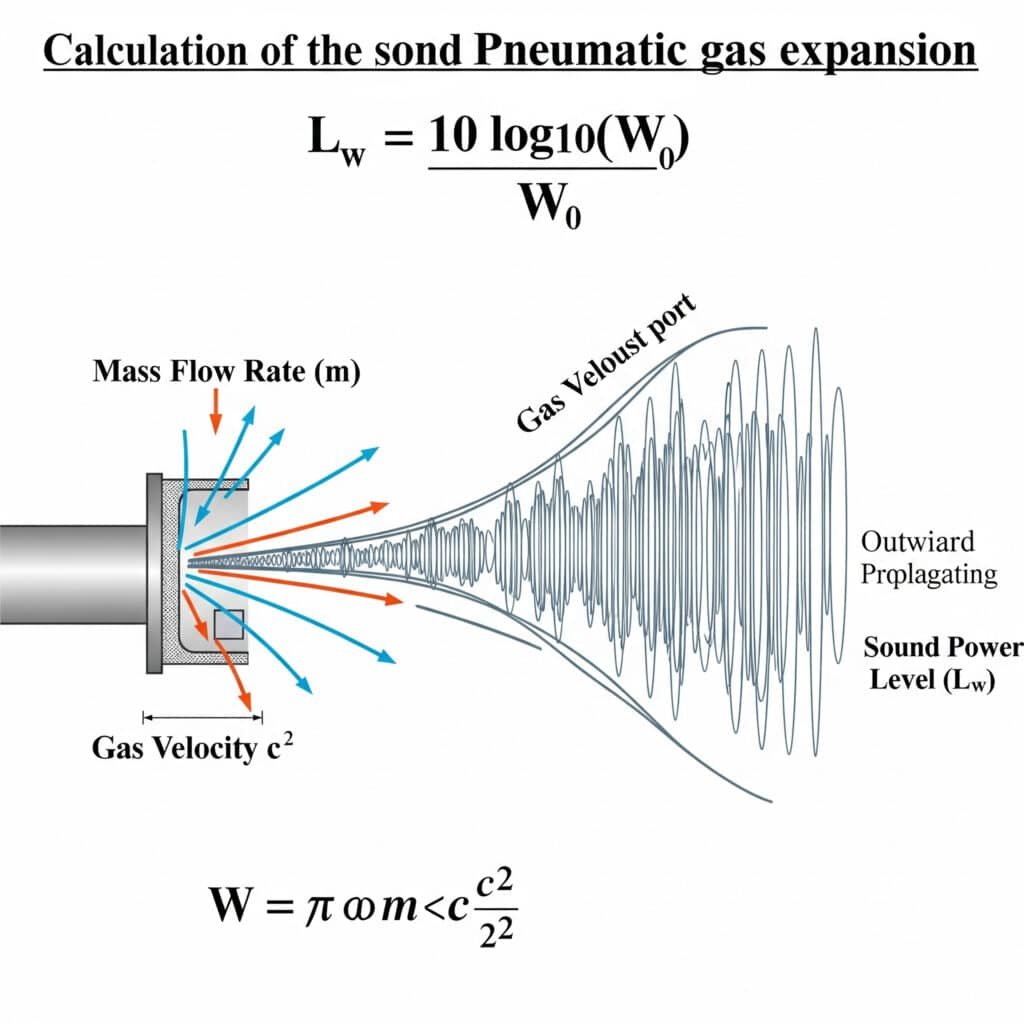
Jeg husker feilsøking på en pakkelinje i Illinois der støynivået oversteg 95 dBA - langt over OSHA-grenser1. Vedlikeholdsteamet hadde fokusert på mekaniske kilder, men vår analyse avslørte at 70% av støyen kom fra eksosportene. Ved å bruke gassekspansjonsformelen fant vi ut at driftstrykket var 2,2 bar høyere enn nødvendig, noe som skapte for mye eksosstøy. Denne enkle trykkjusteringen reduserte støyen med 8 dBA uten å påvirke ytelsen.
Grunnleggende ligninger for støy ved gassekspansjon
La oss se nærmere på de viktigste formlene for å forutsi ekspansjonsstøy:
Beregning av lydeffekt
Den akustiske effekten som genereres av ekspanderende gass, kan beregnes som
W = η × m × (c²/2)
Hvor?
- W = akustisk effekt (watt)
- η = Akustisk virkningsgrad (vanligvis 0,001-0,01 for pneumatiske utblåsninger)
- m = Massestrømningshastighet (kg/s)
- c = Gasshastighet ved eksos (m/s)
Lydeffektnivået i desibel er da:
Lw = 10 log₁₀(W/W₀)
Der W₀ er referanseeffekten på 10¹² watt.
Bestemmelse av massestrømningshastighet
Massestrømmen gjennom en åpning kan beregnes som
m = Cd × A × p₁ × √(2γ/(γ-1) × (RT₁) × [(p₂/p₁)^(2/γ) - (p₂/p₁)^((γ+1)/γ)])
Hvor?
- Cd = utløpskoeffisient (vanligvis 0,6-0,8)
- A = åpningsareal (m²)
- p₁ = absolutt oppstrømstrykk (Pa)
- p₂ = absolutt trykk nedstrøms (Pa)
- γ = Spesifikt varmeforhold (1,4 for luft)
- R = gasskonstant for luft (287 J/kg-K)
- T₁ = temperatur oppstrøms (K)
For strupet strømning (vanlig i pneumatiske utblåsninger) forenkles dette til
m = Cd × A × p₁ × √(γ/(RT₁)) × (2/(γ+1))^((γ+1)/(2(γ-1))))
Faktorer som påvirker støy fra gassekspansjon
| Faktor | Innvirkning på støynivået | Tilnærming til avbøtende tiltak |
|---|---|---|
| Driftstrykk | 3-4 dBA økning per bar | Reduser systemtrykket til det minimum som kreves |
| Størrelse på eksosporten | Mindre porter øker hastigheten og støyen | Bruk porter av riktig størrelse for strømningskravene |
| Eksostemperatur | Høyere temperaturer øker støyen | Tillat avkjøling før utvidelse der det er mulig |
| Ekspansjonsforhold | Høyere forholdstall skaper mer støy | Etappeutvidelse gjennom flere trinn |
| Strømningshastighet | Dobling av strømningshastigheten øker støyen med ~3 dBA | Bruk flere mindre avtrekk i stedet for ett stort |
Praktisk eksempel på støyprediksjon
For en typisk stangløs sylinder med:
- Driftstrykk: 6 bar (600 000 Pa)
- Diameter på eksosporten: 4 mm (areal = 1,26 × 10-⁵ m²)
- Utslippskoeffisient: 0,7
- Akustisk effektivitet: 0,005
Massestrømmen under eksos vil være omtrent:
m = 0,7 × 1,26 × 10-⁵ × 600 000 × 0,0404 = 0,0214 kg/s
Hvis vi antar en eksoshastighet på 343 m/s (sonisk hastighet), vil den akustiske effekten være
W = 0,005 × 0,0214 × (343²/2) = 6,29 watt
Det resulterende lydeffektnivået:
Lw = 10 log₁₀(6,29/10-¹²) = 128 dB
Det høye lydeffektnivået forklarer hvorfor trykkluftavtrekk uten lyddemping er en så betydelig støykilde i industrimiljøer.
Mekanisk vibrasjonsspektrum: Hvordan kan frekvensanalyse identifisere støykilder?
Mekaniske vibrasjoner i pneumatiske komponenter genererer særegne støysignaturer som kan analyseres for å lokalisere spesifikke problemer. Frekvensspekteranalyse er nøkkelen til å identifisere og håndtere disse mekaniske støykildene.
Mekaniske vibrasjoner i pneumatiske systemer produserer støy med karakteristiske frekvensspektre som kan analyseres ved hjelp av Rask Fourier-transformasjon (FFT)2 teknikker. De viktigste frekvensområdene omfatter lavfrekvente strukturelle vibrasjoner (10-100 Hz), mellomfrekvente driftsharmoniske vibrasjoner (100-1000 Hz) og høyfrekvente strømningsinduserte vibrasjoner (1-10 kHz), som alle krever ulike metoder for å redusere vibrasjonene.
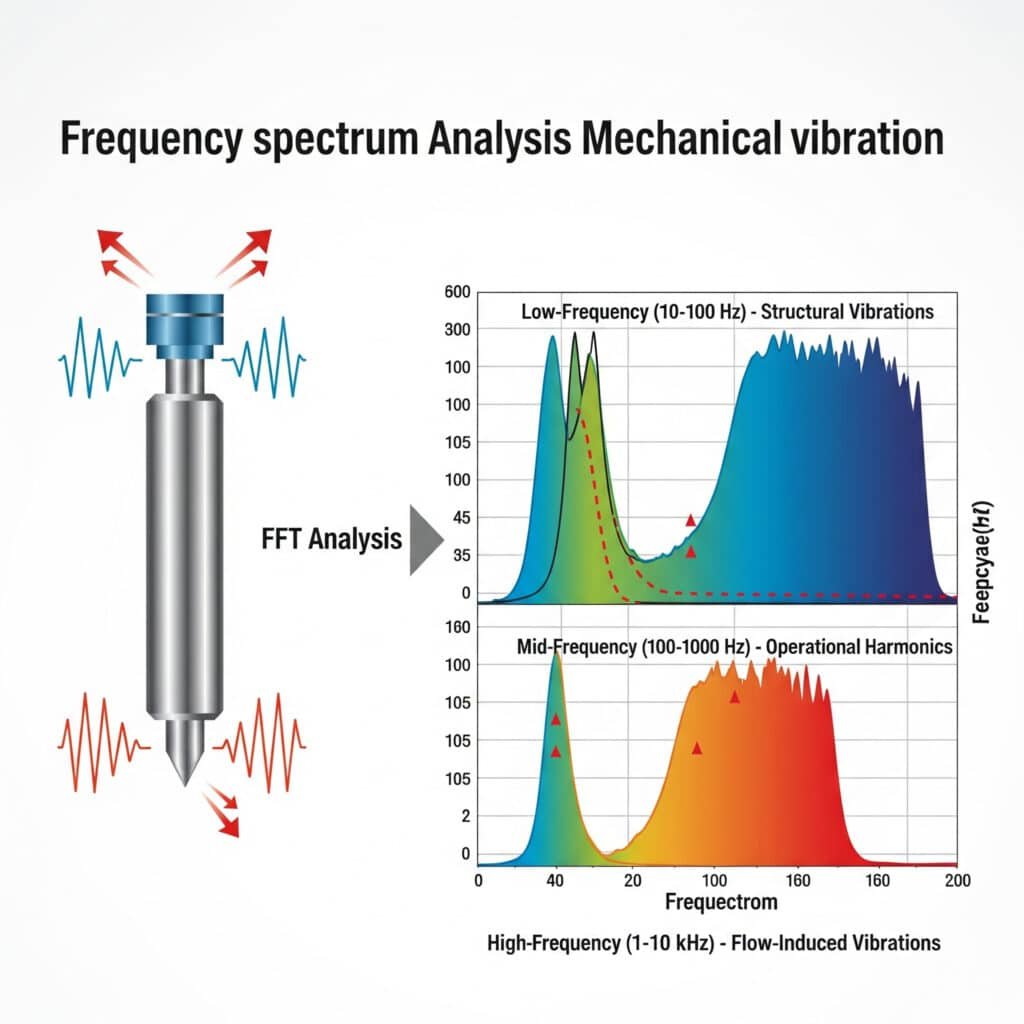
Under en konsultasjon hos en bildelprodusent i Michigan slet vedlikeholdsteamet med overdreven støy fra et stangløst sylinderoverføringssystem. Konvensjonell feilsøking hadde ikke klart å identifisere kilden. Vår vibrasjonsspektrumanalyse avslørte en tydelig topp ved 237 Hz - nøyaktig det samme som sylinderens interne tetningsbåndresonans. Ved å modifisere monteringssystemet for å dempe denne spesifikke frekvensen, reduserte vi støyen med 11 dBA uten produksjonsavbrudd.
Metodikk for frekvensspektrumsanalyse
En effektiv vibrasjonsanalyse følger en systematisk tilnærming:
- Oppsett av måling: Bruk av akselerometre og akustiske mikrofoner
- Datainnsamling: Registrering av vibrasjonssignaler i tidsdomenet
- FFT-analyse: Konvertering til frekvensdomenet
- Spektral kartlegging: Identifisere karakteristiske frekvenser
- Kildeangivelse: Tilpasse frekvenser til spesifikke komponenter
Karakteristiske frekvensområder i pneumatiske systemer
| Frekvensområde | Typiske kilder | Akustiske egenskaper |
|---|---|---|
| 10-50 Hz | Strukturell resonans, monteringsproblemer | Lavfrekvent rumling, mer følbar enn hørbar |
| 50-200 Hz | Stempelpåvirkning, ventilaktivering | Tydelig dunking eller banking |
| 200-500 Hz | Friksjon i tetninger, intern resonans | Mellomfrekvent summende eller brummende lyd |
| 500-2000 Hz | Strømningsturbulens, trykkpulsasjoner | Hissing med tonale komponenter |
| 2-10 kHz | Lekkasje, høy strømningshastighet | Skarp hvesing, svært irriterende for det menneskelige øret |
| >10 kHz | Mikroturbulens, gassekspansjon | Ultralydkomponenter, indikator for energitap |
Overføringsveier for vibrasjoner
Støy fra mekaniske vibrasjoner følger flere veier:
Strukturbåren overføring
Vibrasjoner beveger seg gjennom faste komponenter:
- Komponenten vibrerer på grunn av indre krefter
- Vibrasjonsoverføring gjennom monteringspunkter
- Sammenkoblede strukturer forsterker og utstråler lyd
- Store flater fungerer som effektive lydradiatorer
Luftbåren overføring
Direkte stråling av lyd fra vibrerende overflater:
- Overflatevibrasjon fortrenger luft
- Forskyvning skaper trykkbølger
- Bølger forplanter seg gjennom luft
- Størrelsen på den strålende overflaten avgjør effektiviteten
Casestudie: Vibrasjonsanalyse av stangløse sylindere
For en magnetisk stangløs sylinder som viser overdreven støy:
| Frekvens (Hz) | Amplitude (dB) | Kildeidentifikasjon | Strategi for avbøtende tiltak |
|---|---|---|---|
| 43 | 78 | Montering av resonans | Avstivet monteringsbrakett |
| 86 | 65 | Harmonisk av monteringsresonans | Adressert med primær resonans |
| 237 | 91 | Forseglingsbåndresonans | Lagt til dempemateriale i sylinderhuset |
| 474 | 83 | Harmonisk av tetningsbånd | Adressert med primær resonans |
| 1250 | 72 | Turbulens i luftstrømmen | Modifisert portdesign |
| 3700 | 68 | Lekkasje ved endestykker | Utskiftede tetninger |
De kombinerte tiltakene reduserte den totale støyen med 14 dBA, og den største forbedringen kom fra 237 Hz-resonansen.
Avanserte teknikker for vibrasjonsanalyse
I tillegg til grunnleggende FFT-analyse finnes det flere avanserte teknikker som gir dypere innsikt:
Ordreanalyse
Spesielt nyttig for systemer med variabel hastighet:
- Sporer frekvenser som skalerer med driftshastigheten
- Skiller hastighetsavhengige fra fastfrekvente komponenter
- Identifiserer problemer knyttet til spesifikke bevegelsesfaser
Analyse av operasjonell avbøyningsform (ODS)
Kartlegger vibrasjonsmønstre over hele systemet:
- Flere målepunkter skaper et "vibrasjonskart"
- Avslører hvordan strukturer beveger seg under drift
- Identifiserer optimale steder for dempebehandlinger
Modal analyse
Bestemmer egenfrekvenser og modusformer:
- Identifiserer resonansfrekvenser før drift
- Forutser potensielle problemfrekvenser
- Styrer strukturelle endringer for å unngå resonans
Innsettingstap i lyddempere: Hvilke beregninger ligger til grunn for effektiv lyddemperdesign?
Lyddempere og lyddempere er avgjørende for å redusere støy fra pneumatiske systemer, men utformingen av dem må være basert på lydtekniske beregninger for å sikre effektivitet uten at det går ut over systemets ytelse.
Lyddemper innsettingstap3 (IL) kvantifiserer effektiviteten av støyreduksjonen og kan beregnes som IL = Lw₁ - Lw₂, der Lw₁ er lydeffektnivået uten lyddemper og Lw₂ er nivået med lyddemperen installert. For pneumatiske systemer oppnår effektive lyddempere vanligvis 15-30 dB innsettingstap over det kritiske frekvensområdet 500 Hz til 4 kHz, samtidig som de opprettholder et akseptabelt mottrykk.
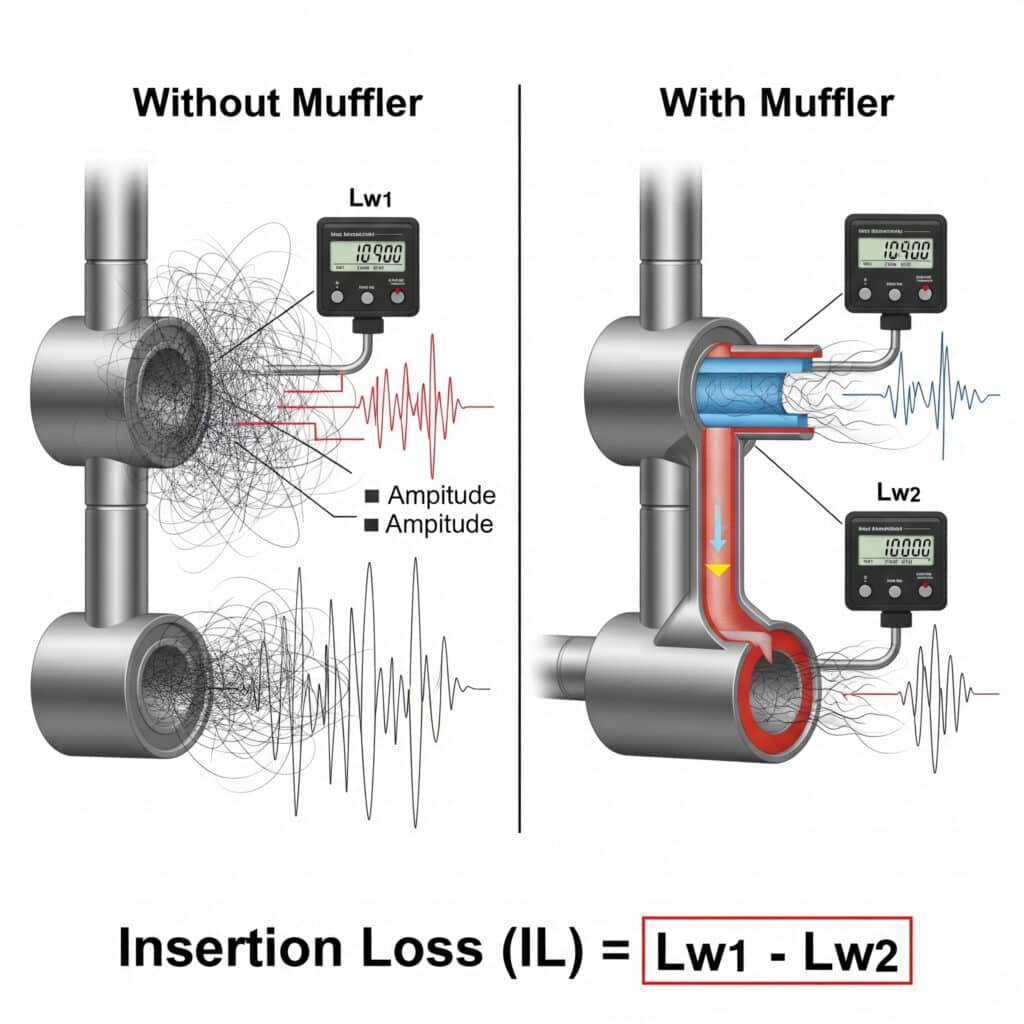
Jeg hjalp nylig en produsent av medisinsk utstyr i Massachusetts med å løse et utfordrende støyproblem med deres presisjonssylindersystem uten stenger. Det første forsøket på å bruke standard lyddempere reduserte støyen, men skapte et for høyt mottrykk som påvirket syklustidene. Ved å beregne det nødvendige innsettingstapet i bestemte frekvensbånd og designe en spesialtilpasset lyddemper med flere kamre oppnådde vi en støyreduksjon på 24 dB med minimal innvirkning på ytelsen. Resultatet var et system som oppfylte både støy- og presisjonskravene.
Grunnleggende om innsettingstap i lyddempere
Kjerneligningen for innsettingstap er
IL = Lw₁ - Lw₂
Hvor?
- IL = innsettingstap (dB)
- Lw₁ = lydeffektnivå uten lyddemper (dB)
- Lw₂ = lydeffektnivå med lyddemper (dB)
For frekvensspesifikk analyse blir dette:
IL(f) = Lw₁(f) - Lw₂(f)
Der f angir det spesifikke frekvensbåndet som analyseres.
Parametere for lyddemperdesign og deres innvirkning
| Parameter | Effekt på innsettingstap | Effekt på mottrykket | Optimal rekkevidde |
|---|---|---|---|
| Kammervolum | Større volum øker lavfrekvent IL | Minimal innvirkning hvis den er riktig utformet | 10-30× eksosportens volum |
| Antall kamre | Flere kamre øker mellomfrekvensen IL | Øker med flere kamre | 2-4 kamre for de fleste bruksområder |
| Ekspansjonsforhold | Høyere forholdstall forbedrer IL | Minimal innvirkning hvis gradvis | 4:1 til 16:1 arealforhold |
| Akustisk materiale | Forbedrer høyfrekvent IL | Minimal innvirkning med riktig design | 10-50 mm tykkelse |
| Baffelperforering | Påvirker mellomfrekvent IL | Betydelig innvirkning | 30-50% åpent område |
| Strømningsveiens lengde | Lengre traséer forbedrer lavfrekvent IL | Øker med lengden | 3-10× portdiameter |
Teoretiske modeller for prediksjon av innskjæringstap
Flere modeller kan forutsi innsettingstap for ulike lyddempertyper:
Modell for ekspansjonskammer
For enkle ekspansjonskamre:
IL = 10 log₁₀[1 + 0,25(m-1/m)² sin²(kL)]
Hvor?
- m = arealforhold (kammerareal / rørareal)
- k = Bølgetall (2πf/c, der f er frekvens og c er lydhastighet)
- L = kammerets lengde
Dissipativ lyddempermodell
For lyddempere med lydabsorberende materialer:
IL = 8,68α(L/d)
Hvor?
- α = Absorpsjonskoeffisient for materialet
- L = Lengden på den forede delen
- d = diameter på strømningsbanen
Reaktiv lyddempermodell (Helmholtz-resonator4)
For lyddempere av resonatortypen:
IL = 10 log₁₀[1 + (ρc/2S)² × (V/L'c²) × ω²/((ω₀² - ω²)² + (Rω/ρc)²)]
Hvor?
- ρ = Lufttetthet
- c = lydens hastighet
- S = Halsens tverrsnittsareal
- V = hulromsvolum
- L' = effektiv halslengde
- ω = vinkelfrekvens
- ω₀ = Resonansfrekvens
- R = Akustisk motstand
Praktisk prosess for valg av lyddemper
For å velge eller designe en passende lyddemper:
- Mål støyspekteret: Bestem frekvensinnholdet i støyen
- Beregn nødvendig IL: Bestem nødvendig reduksjon etter frekvens
- Vurder behovet for flyt: Beregn maksimalt tillatt mottrykk
- Velg type lyddemper:
- Reaktive (ekspansjonskamre) for lave frekvenser
- Dissipativ (absorberende) for høye frekvenser
- Kombinasjon for bredbåndsstøy - Verifiser ytelse: Test innsettingstap og mottrykk
Hensyn til mottrykk
For høyt mottrykk kan påvirke systemets ytelse betydelig:
Beregning av mottrykk
Mottrykket kan beregnes som:
ΔP = ρ(Q/Cd×A)²/2
Hvor?
- ΔP = Trykkfall (Pa)
- ρ = Luftens tetthet (kg/m³)
- Q = Strømningshastighet (m³/s)
- Cd = Utslippskoeffisient
- A = Effektivt strømningsareal (m²)
Vurdering av ytelsens innvirkning
For en stangløs sylinder med:
- Borediameter: 40 mm
- Slaglengde 500 mm
- Syklustid: 2 sekunder
- Driftstrykk: 6 bar
Hvert 0,1 bar mottrykk vil
- Reduser kraftuttaket med ca. 1,7%
- Øker syklustiden med ca. 2,3%
- Øker energiforbruket med ca. 1,5%
Casestudie: Design av spesialtilpassede lyddempere
For presisjonsapplikasjoner med stangløse sylindere med strenge støykrav:
| Parameter | Opprinnelig tilstand | Standard lyddemper | Tilpasset design |
|---|---|---|---|
| Lydnivå | 89 dBA | 76 dBA | 65 dBA |
| Mottrykk | 0,05 bar | 0,42 bar | 0,11 bar |
| Syklustid | 1,8 sekunder | 2,3 sekunder | 1,9 sekunder |
| Frekvensrespons | Bredbånd | Dårlig ved 2-4 kHz | Optimalisert på tvers av spekteret |
| Levetid | N/A | 3 måneder (tilstopping) | >12 måneder |
| Implementeringskostnader | N/A | $120 per punkt | $280 per punkt |
Den spesialtilpassede lyddemperen ga overlegen støyreduksjon samtidig som den opprettholdt akseptabel systemytelse, med en avkastning på investeringen på mindre enn 6 måneder når man tar hensyn til produktivitetsforbedringer.
Konklusjon
Forståelse av akustiske støygenereringsmekanismer - lydnivåer fra gassekspansjon, mekaniske vibrasjonsspektre og beregninger av innsettingstap i lyddempere - danner grunnlaget for effektiv støykontroll i pneumatiske systemer. Ved å bruke disse prinsippene kan du skape mer stillegående, effektive og pålitelige pneumatiske systemer, samtidig som du sikrer overholdelse av lover og regler og forbedrer forholdene på arbeidsplassen.
Vanlige spørsmål om støy fra pneumatiske systemer
Hva er OSHA-grensene for eksponering for støy fra pneumatiske systemer?
OSHA begrenser støyeksponeringen på arbeidsplassen til 90 dBA for et 8-timers tidsvektet gjennomsnitt, med en utvekslingskurs på 5 dBA. NIOSHs anbefalte grenseverdi er imidlertid mer konservativ, på 85 dBA. Pneumatiske systemer overskrider ofte disse grenseverdiene, med lydløse eksosrør som ofte genererer 90-110 dBA på én meters avstand, noe som krever tekniske tiltak for å overholde grensene.
Hvordan påvirker driftstrykket støy fra pneumatiske systemer?
Driftstrykket har en betydelig innvirkning på støygenereringen, og hver økning i trykket på 1 bar øker vanligvis eksosstøynivået med 3-4 dBA. Dette forholdet er logaritmisk snarere enn lineært, ettersom lydeffekten øker med kvadratet av trykkforholdet. Den enkleste og mest kostnadseffektive strategien for støyreduksjon er ofte å redusere systemtrykket til det minimum som kreves for drift.
Hva er forskjellen mellom reaktive og dissipative lyddempere for pneumatiske systemer?
Reaktive lyddempere bruker kamre og passasjer til å reflektere lydbølger og skape destruktiv interferens, noe som gjør dem effektive for lavfrekvent støy (under 500 Hz) med minimalt trykkfall. Dissipative lyddempere bruker lydabsorberende materialer til å omdanne akustisk energi til varme, noe som gjør dem mer effektive for høyfrekvent støy (over 500 Hz), men mer utsatt for forurensning. Mange industrielle pneumatiske lyddempere kombinerer begge prinsippene for å redusere bredbåndsstøy.
Hvordan kan jeg identifisere den dominerende støykilden i det pneumatiske systemet mitt?
Bruk en systematisk tilnærming som starter med driftstesting: Kjør systemet ved ulike trykk, hastigheter og belastninger mens du måler støy. Deretter isolerer du komponentene ved å kjøre de enkelte elementene hver for seg. Til slutt kan du gjennomføre en frekvensanalyse ved hjelp av en lydnivåmåler med oktavbåndkapasitet - lave frekvenser (50-250 Hz) indikerer vanligvis strukturelle problemer, mellomfrekvenser (250-2000 Hz) tyder på driftsstøy, og høye frekvenser (2-10 kHz) tyder på strømnings- eller lekkasjeproblemer.
Hva er forholdet mellom støynivå og avstand fra en pneumatisk komponent?
Støy fra pneumatiske komponenter følger den omvendte kvadratiske loven i fritt felt, og reduseres med omtrent 6 dB for hver gang avstanden dobles. I typiske industrimiljøer med reflekterende overflater er imidlertid den faktiske reduksjonen ofte bare 3-4 dB per dobling av avstanden på grunn av etterklang. Dette betyr at en dobling av avstanden fra en støykilde på 90 dB kanskje bare reduserer nivået til 86-87 dB i stedet for det teoretiske 84 dB.
-
Her finner du de offisielle OSHA-forskriftene (Occupational Safety and Health Administration) og tillatte eksponeringsgrenser (PEL) for støy på arbeidsplassen, noe som er en viktig drivkraft for akustisk demping. ↩
-
Forklarer Fast Fourier Transform (FFT)-algoritmen, et viktig matematisk verktøy som brukes til å konvertere et tidssignal (f.eks. en vibrasjon eller lydbølge) til de enkelte frekvenskomponentene som inngår i analysen. ↩
-
Beskriver modalanalyse, en avansert ingeniørteknikk som brukes til å bestemme de iboende dynamiske egenskapene til et system, for eksempel dets egenfrekvenser og modusformer, for å forutsi og unngå resonans. ↩
-
Gir en detaljert forklaring av Insertion Loss (IL), det primære målet som brukes til å kvantifisere ytelsen til en lyddemper ved å måle lydnivåreduksjonen den gir. ↩



