
Sliter du med inkonsekvente pneumatiske sylinderhastigheter eller uventede slag ved slutten av slaget? Disse vanlige problemene skyldes ofte dårlig forståelse av stempelkinematikk. Mange ingeniører fokuserer utelukkende på kraftkravene, mens de overser de kritiske bevegelsesparameterne som er avgjørende for systemets ytelse.
Stempelkinematikk1 har direkte innvirkning på pneumatiske systemers ytelse gjennom trykk-hastighetsforhold, akselerasjonsgrenser og krav til demping. Ved å forstå disse prinsippene kan ingeniører dimensjonere komponenter riktig, forutsi faktiske bevegelsesprofiler og forhindre for tidlig svikt i sylindere uten stang og andre pneumatiske aktuatorer.
I løpet av de mer enn 15 årene jeg har jobbet med pneumatiske systemer i Bepto, har jeg sett utallige tilfeller der forståelsen av disse grunnleggende prinsippene har hjulpet kundene med å løse vedvarende ytelsesproblemer og forlenge utstyrets levetid med 3-5 ganger.
Innholdsfortegnelse
- Hvilket trykk trenger du egentlig for konstant hastighet?
- Hvordan beregner du maksimal akselerasjon i pneumatiske sylindere?
- Hvorfor er det viktig med dempingstid, og hvordan beregnes den?
- Konklusjon
- Vanlige spørsmål om stempelkinematikk i pneumatiske systemer
Hvilket trykk trenger du egentlig for konstant hastighet?
Mange ingeniører bruker bare maksimalt tilgjengelig trykk på de pneumatiske systemene sine, men denne tilnærmingen er ineffektiv og kan føre til rykkvise bevegelser, overdreven slitasje og bortkastet energi.
Trykket som kreves for konstant hastighet i en pneumatisk sylinder, beregnes ved hjelp av P = (F + Fr)/A, der P er trykket, F er den ytre belastningskraften, Fr er friksjonsmotstanden og A er stempelarealet. Denne beregningen sikrer jevn og effektiv drift uten for høyt trykk som sløser med energi og øker slitasjen på komponentene.
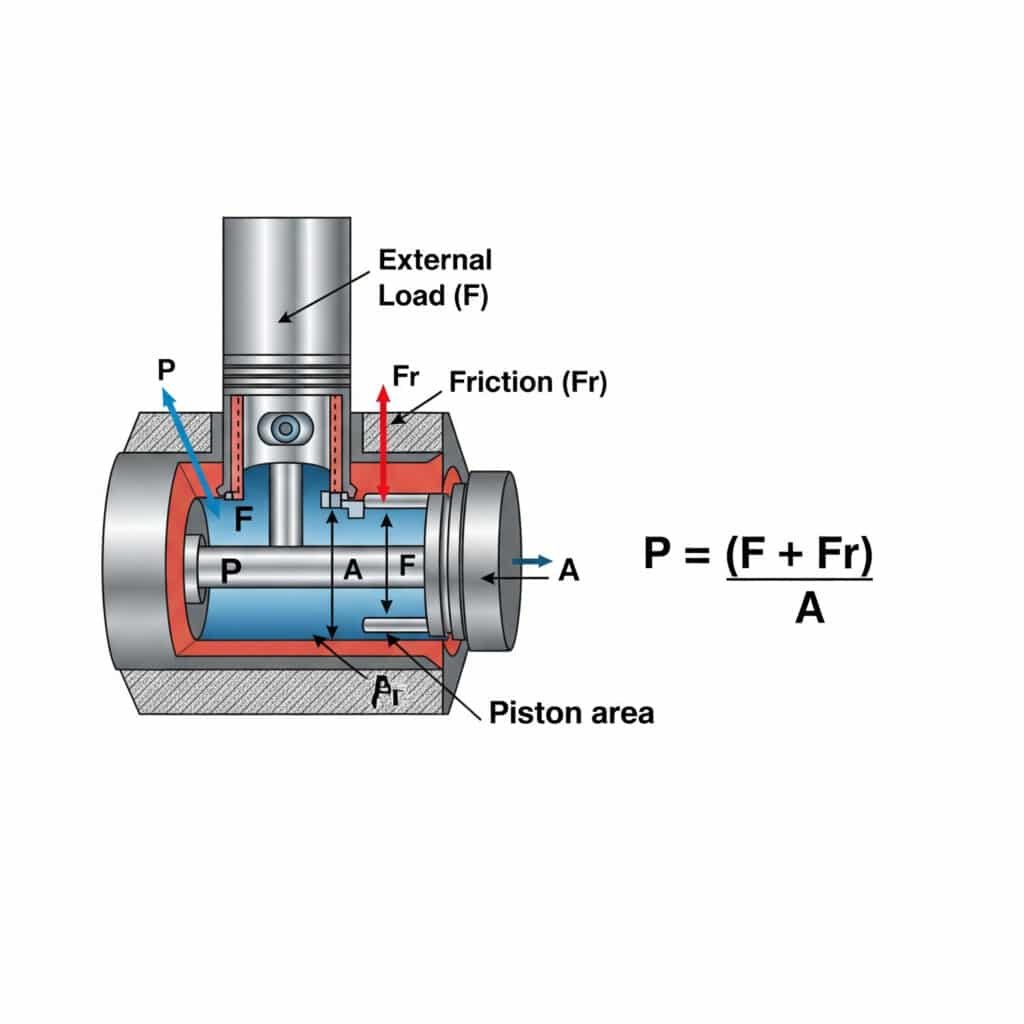
Å forstå trykkkravene for bevegelse med konstant hastighet har praktiske konsekvenser for systemdesign og drift. La meg bryte dette ned i praktisk anvendelig innsikt.
Faktorer som påvirker trykkbehovet for konstant hastighet
Trykket som trengs for å opprettholde konstant hastighet, avhenger av flere faktorer:
| Faktor | Innvirkning på trykkbehovet | Praktisk betraktning |
|---|---|---|
| Ekstern belastning | Direkte lineær sammenheng | Varierer med orientering og ytre krefter |
| Friksjon | Øker det nødvendige trykket | Endringer med tetningsslitasje og smøring |
| Stempelområde | Omvendt proporsjonal | Større boring = lavere trykkbehov |
| Begrensninger i lufttilførselen | Trykkfall i ledninger/ventiler | Dimensjoner komponenter for minimalt trykkfall |
| Mottrykk | Er imot forslaget | Vurder eksosstrømkapasiteten |
Beregning av minimumstrykk for stabil bevegelse
For å bestemme det minste trykket som trengs for stabil bevegelse:
- Beregn kraften som kreves for å overvinne den ytre belastningen
- Legg til friksjonskraften (vanligvis 3-20% av maksimal kraft)
- Divider med det effektive stempelområdet
- Legg til en stabilitetsfaktor (vanligvis 10-30%)
For eksempel i en sylinder uten stang med 40 mm boring, 10 kg belastning og 15% friksjon:
| Parameter | Beregning | Resultat |
|---|---|---|
| Belastningskraft | 10 kg × 9,81 m/s² | 98.1N |
| Friksjonskraft | 15% av maksimal kraft ved 6 bar | ~45N |
| Total styrke | 98,1N + 45N | 143.1N |
| Stempelområde | π × (0,02m)² | 0.00126m² |
| Minimumstrykk | 143,1N ÷ 0,00126m² | 113 571 Pa (1,14 bar) |
| Med 20% Stabilitetsfaktor | 1,14 bar × 1,2 | 1,37 bar |
Anvendelse i den virkelige verden: Energibesparelser gjennom trykkoptimalisering
I fjor jobbet jeg sammen med Robert, en produksjonsingeniør ved en møbelproduksjon i Michigan. Det automatiserte samlebåndet hans brukte sylindere uten stang som kjørte med hele 6 bars forsyningstrykk, uavhengig av belastning.
Etter å ha analysert applikasjonen hans fant vi ut at de fleste bevegelser bare krevde 2,5-3 bar for stabil drift. Ved å installere proporsjonale trykkregulatorerreduserte vi luftforbruket med 40% samtidig som vi opprettholdt samme syklustid. Dette sparte ca. $12 000 i energikostnader årlig, samtidig som vi reduserte tetningsslitasje og forlenget vedlikeholdsintervallene.
Forholdet mellom hastighet og trykk i virkelige systemer
I praksis er forholdet mellom trykk og hastighet ikke helt lineært på grunn av:
- Strømningsbegrensninger: Ventil- og portdimensjonering påvirker maksimal oppnåelig hastighet
- Kompressibilitetseffekter: Luft er komprimerbar, noe som forårsaker akselerasjonsforsinkelser
- Stick-slip-fenomener: Friksjonsegenskapene endres med hastigheten
- Treghetseffekter: Masseakselerasjon krever ekstra kraft/trykk
Hvordan beregner du maksimal akselerasjon i pneumatiske sylindere?
Det er avgjørende å forstå akselerasjonsgrensene for å unngå for store støt, vibrasjoner og for tidlig svikt i komponenter i pneumatiske systemer.
Den maksimalt mulige akselerasjonen i en pneumatisk sylinder beregnes ved hjelp av a = (P × A - F - Fr)/m, der a er akselerasjon, P er trykk, A er stempelareal, F er ytre belastning, Fr er friksjonsmotstand, og m er den bevegelige massen. Denne ligningen definerer de fysiske grensene for hvor raskt en pneumatisk aktuator kan starte eller stoppe en bevegelse.
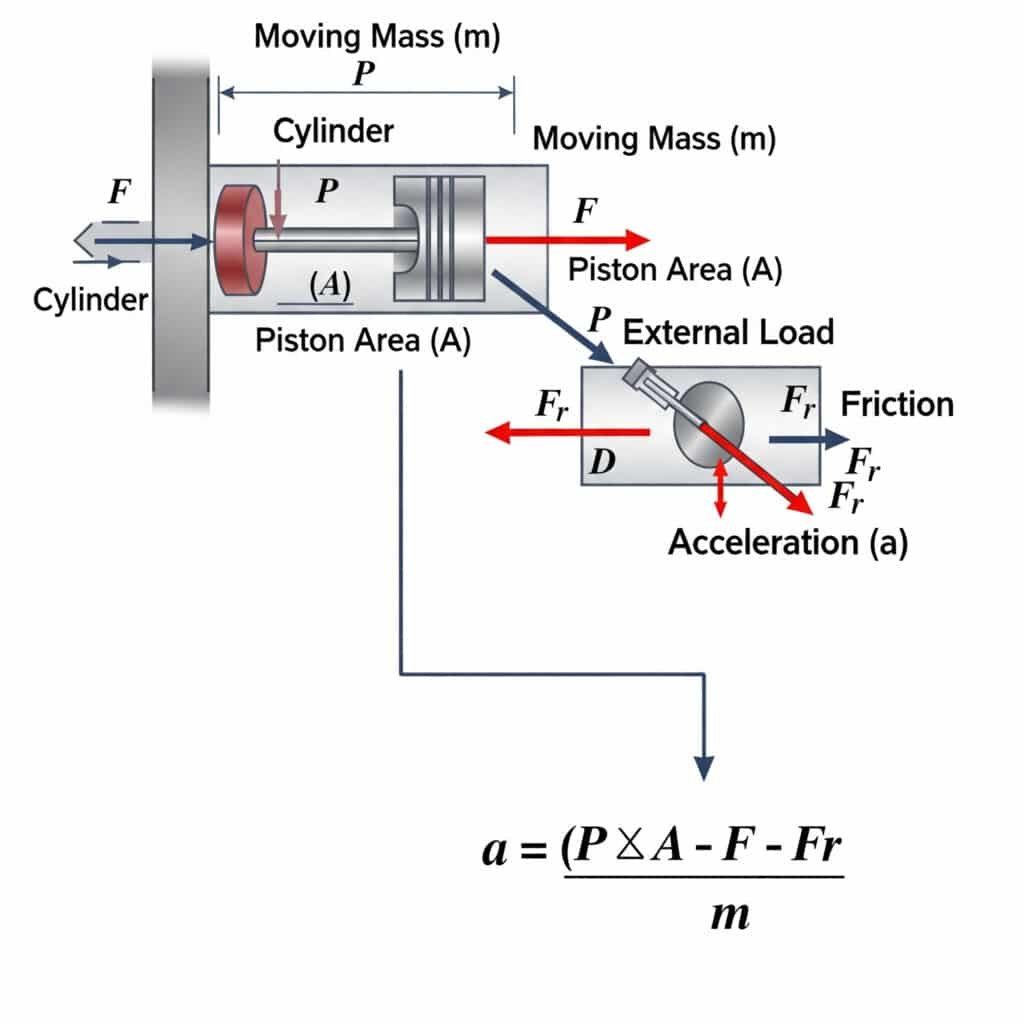
De teoretiske akselerasjonsgrensene har betydelige praktiske konsekvenser for systemdesign og valg av komponenter.
Utledning av akselerasjonsgrenselikningen
Akselerasjonsgrenseligningen kommer fra Newtons andre lov2 (F = ma):
- Nettokraften som er tilgjengelig for akselerasjon, er Fnet = Ftrykk - Flast - Ffriksjon
- F-trykk = P × A
- Derfor: a = Fnet/m = (P × A - F - Fr)/m
Praktiske akselerasjonsgrenser for ulike flasketyper
Ulike sylinderkonstruksjoner har ulike praktiske akselerasjonsgrenser:
| Sylindertype | Typisk maks akselerasjon | Begrensende faktorer |
|---|---|---|
| Standard stangsylinder | 10-15 m/s² | Knekking av stang, lagerbelastninger |
| Sylinder uten stang (magnetisk) | 8-12 m/s² | Magnetisk koblingsstyrke |
| Stangløs sylinder (mekanisk) | 15-25 m/s² | Utforming av tetning/lager, intern friksjon |
| Føringssylinder | 20-30 m/s² | Styresystemets stivhet og bæreevne |
| Slagsylinder | 50-100+ m/s² | Spesielt utviklet for høy akselerasjon |
Massehensyn i akselerasjonsberegninger
Når du beregner akselerasjon, er det viktig å ta med alle bevegelige masser:
- Stempelenhet: Inkluderer stempel, tetninger og forbindelseselementer
- Last masse: Ekstern last som flyttes
- Effektiv masse av luft i bevegelse: Ofte ubetydelig, men relevant i høyhastighetsapplikasjoner
- Ekstra masse på grunn av monteringskomponenter: Braketter, sensorer osv.
En gang hjalp jeg en kunde i Frankrike som opplevde mystiske feil i det stangløse sylindersystemet sitt. Sylinderen var riktig dimensjonert for den oppgitte belastningen på 15 kg, men sviktet konsekvent etter noen tusen sykluser.
Etter å ha undersøkt saken, oppdaget vi at han hadde glemt å ta hensyn til massen på 12 kg fra monteringsplaten og festene. Den faktiske bevegelige massen var nesten dobbelt så stor som han hadde beregnet, noe som førte til akselerasjonskrefter som oversteg sylinderens konstruksjonsgrenser. Etter at vi oppgraderte til en større sylinder, opphørte feilene helt.
Metoder for akselerasjonskontroll
For å kontrollere akselerasjonen innenfor sikre grenser:
- Strømningsreguleringsventiler: Begrens strømningshastigheten under første bevegelse
- Proporsjonale ventiler: Gir kontrollert trykkøkning
- Akselerasjon i flere trinn: Bruk trinnvise trykkøkninger
- Mekanisk demping: Legg til eksterne støtdempere
- Elektronisk kontroll: Bruk servo-pneumatiske systemer3 med akselerasjonstilbakemelding
Hvorfor er det viktig med dempingstid, og hvordan beregnes den?
Riktig demping ved slutten av slaget er avgjørende for å forhindre støtskader, redusere støy og forlenge levetiden til pneumatiske sylindere. Forståelse av dempingstiden hjelper ingeniører med å designe systemer som balanserer syklustiden med komponentens levetid.
Dempingstiden i pneumatiske sylindere beregnes ved hjelp av ligningen t = √(2s/a), der t er tid, s er lengden på dempingsslaget og a er retardasjon. Denne tiden representerer hvor lang tid det tar å bremse ned den bevegelige massen på en sikker måte før sammenstøtet, noe som er avgjørende for å forhindre skade på sylinderen og tilhørende komponenter.

La oss se nærmere på de praktiske aspektene ved beregning av dempetid og hva dette innebærer for systemdesign.
Fysikken bak pneumatisk demping
Pneumatisk demping fungerer gjennom kontrollert luftkompresjon og begrenset utblåsning:
- Når stempelet går inn i putekammeret, begrenses eksosveien
- Luften som er fanget komprimeres, noe som skaper et økende mottrykk
- Dette mottrykket skaper en motkraft som bremser stempelet
- Retardasjonsprofilen avhenger av putenes utforming og justering
Beregning av optimal dempetid
Den optimale dempetiden balanserer støtforebygging med effektiv syklustid:
| Parameter | Formel | Eksempel |
|---|---|---|
| Dempende avstand | Basert på sylinderdesign | 15 mm (typisk for 40 mm boring) |
| Nødvendig retardasjon | a = v²/(2s) | For v=0,5 m/s, s=15 mm: a = 8,33 m/s² |
| Dempende tid | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Oppbygging av trykk | P = P₀(V₀/V)^γ | Avhenger av putekammerets geometri |
Faktorer som påvirker dempingens ytelse
Flere faktorer påvirker den faktiske dempingsevnen:
- Design med puteforsegling: Påvirker luftlekkasje under demping
- Justering av nåleventilen: Kontrollerer eksosbegrensningshastigheten
- Masse i bevegelse: Tyngre laster krever lengre dempingstid
- Innflygingshastighet: Høyere hastigheter krever lengre puteavstand
- Driftstrykk: Påvirker maksimal motkraft tilgjengelig
Typer demping og bruksområder
Ulike dempingsmekanismer egner seg for ulike bruksområder:
| Type demping | Kjennetegn | Beste bruksområder |
|---|---|---|
| Fastmontert demping | Enkel, ikke-justerbar | Lette belastninger, jevn drift |
| Justerbar demping | Avstemmbar med nåleventiler | Varierende belastninger, fleksible bruksområder |
| Selvjusterende demping | Tilpasser seg ulike forhold | Endring av hastigheter og belastninger |
| Utvendige støtdempere | Høy energiabsorpsjon | Tunge laster, høye hastigheter |
| Elektronisk demping | Nøyaktig kontrollert retardasjon | Servopneumatiske systemer |
Casestudie: Optimalisering av demping i applikasjoner med høy syklus
Jeg jobbet nylig med Thomas, en designingeniør hos en produsent av bildeler i Tyskland. Monteringslinjen hans brukte sylindere uten stang som kjørte i 45 sykluser i minuttet, men opplevde hyppige tetningsfeil og skader på monteringsbrakettene.
Analysen viste at dempetiden var for kort for den bevegelige massen, noe som førte til slagkrefter på nesten 3G i hver ende av slaget. Ved å øke dempeslaget fra 12 mm til 20 mm og optimalisere nålventilinnstillingene, forlenget vi dempetiden fra 0,04 s til 0,07 s.
Denne tilsynelatende lille endringen reduserte slagkreftene med over 60%, eliminerte skadene på braketten fullstendig og forlenget tetningens levetid fra tre måneder til over ett år - samtidig som den nødvendige syklustiden ble opprettholdt.
Praktisk prosedyre for justering av demping
For optimal demping i sylindere uten stenger:
- Start med puteventilene helt åpne (minimal restriksjon)
- Steng puteventilen gradvis til en jevn oppbremsing er oppnådd
- Test med forventet minimums- og maksimumsbelastning
- Verifiser dempingens ytelse over hele hastighetsområdet
- Lytt etter støtlyder som indikerer utilstrekkelig demping
- Mål faktisk retardasjonstid for å bekrefte beregningene
Konklusjon
Forståelse av prinsippene for stempelkinematikk - fra trykkkrav for konstant hastighet til akselerasjonsgrenser og beregning av dempetid - er avgjørende for å kunne konstruere effektive og pålitelige pneumatiske systemer. Ved å bruke disse prinsippene på dine stangløse sylinderapplikasjoner kan du optimalisere ytelsen, redusere energiforbruket og forlenge komponentenes levetid betydelig.
Vanlige spørsmål om stempelkinematikk i pneumatiske systemer
Hvilket trykk trenger jeg for en bestemt sylinderhastighet?
Trykket som trengs, avhenger av belastningen, friksjonen og sylinderarealet. Beregn det ved hjelp av P = (F + Fr)/A, der F er den ytre lastkraften, Fr er friksjonsmotstanden og A er stempelarealet. For en typisk sylinder uten stempelstang som beveger en last på 10 kg horisontalt, trenger du ca. 1,5-2 bar for stabil bevegelse ved moderate hastigheter.
Hvor raskt kan en pneumatisk sylinder akselerere?
En pneumatisk sylinders maksimale akselerasjon beregnes ved hjelp av a = (P × A - F - Fr)/m. Typiske sylindere uten stang kan oppnå en akselerasjon på 10-25 m/s², avhengig av konstruksjonen. Dette betyr at en hastighet på 0,5 m/s nås på omtrent 20-50 millisekunder under optimale forhold.
Hvilke faktorer begrenser den maksimale hastigheten til en stangløs sylinder?
Maksimal hastighet begrenses av ventilens strømningskapasitet, lufttilførselsvolum, portstørrelse, dempingsevne og tetningskonstruksjon. De fleste standard stangløse sylindere er konstruert for maksimale hastigheter på 0,8-1,5 m/s, men spesialiserte høyhastighetssylindere kan nå 2-3 m/s.
Hvordan beregner jeg riktig demping for mitt bruksområde?
Beregn riktig demping ved å bestemme den kinetiske energien (KE = ½mv²) til lasten i bevegelse, og sørg for at dempingssystemet kan absorbere denne energien. Dempingstiden bør beregnes ved hjelp av t = √(2s/a), der s er puteavstanden og a er den ønskede retardasjonshastigheten.
Hva skjer hvis den pneumatiske sylinderen min akselererer for raskt?
Overdreven akselerasjon kan føre til mekanisk belastning på monteringskomponenter, for tidlig tetningsslitasje, økt vibrasjon og støy, potensiell lastforskyvning eller skade og redusert systempresisjon. Det kan også føre til rykkete bevegelser som påvirker produktkvaliteten i presisjonsapplikasjoner.
Hvordan påvirker lastretningen trykket som kreves for bevegelse?
Lastens orientering påvirker trykkbehovet i betydelig grad. Vertikale laster som beveger seg mot tyngdekraften, krever ekstra trykk for å overvinne gravitasjonskraften (P = F/A + Fg/A + Fr/A). Horisontale laster trenger bare å overvinne friksjon og treghet. Skråbelastninger faller mellom disse ytterpunktene basert på vinklens sinus.
-
Gir en grunnleggende forklaring på kinematikk, den grenen av mekanikken som beskriver bevegelsen til objekter uten å ta hensyn til kreftene som forårsaker bevegelsen.
elektronisk inngangssignal, noe som muliggjør avansert pneumatisk styring. ↩ -
Detaljer om Newtons andre lov (F=ma), det grunnleggende fysikkprinsippet som relaterer kraften som virker på et objekt til massen og akselerasjonen, og som er grunnlaget for alle dynamiske beregninger. ↩
-
Beskriver servopneumatikk, en avansert styringsteknologi som kombinerer pneumatikkens kraft med presisjonen til elektronisk styring med lukket sløyfe for å oppnå svært nøyaktige posisjonerings- og bevegelsesprofiler. ↩


