
Har du noen gang tatt på en pneumatisk sylinder etter kontinuerlig drift og blitt overrasket over hvor varmt det føles? Denne varmen er ikke bare en ulempe - den representerer bortkastet energi, redusert effektivitet og potensielle problemer med driftssikkerheten som kan koste bedriften din tusenvis av kroner.
Varmeoverføring i pneumatiske systemer skjer gjennom tre mekanismer: ledning gjennom komponentmaterialer, konveksjon mellom overflater og luft, og stråling fra varme overflater. Ved å forstå og optimalisere disse prinsippene kan man redusere driftstemperaturene med 15-30%, forlenge komponentenes levetid med opptil 40% og forbedre energieffektiviteten med 5-15%.
I forrige måned var jeg konsulent for et næringsmiddelanlegg i Georgia der de stangløse sylindrene sviktet hver 3-4 måned på grunn av termiske problemer. Vedlikeholdsteamet byttet bare ut komponenter uten å ta tak i årsaken. Ved å bruke riktige varmeoverføringsprinsipper reduserte vi driftstemperaturen med 22 °C og forlenget levetiden til komponentene til over ett år. La meg vise deg hvordan vi gjorde det - og hvordan du kan bruke de samme prinsippene på dine systemer.
Innholdsfortegnelse
- Beregning av konduksjonskoeffisient: Hvordan beveger varmen seg gjennom komponentene dine?
- Metoder for forbedring av konveksjon: Hvilke teknikker maksimerer luft-til-overflate-varmeoverføring?
- Modell for strålingseffektivitet: Når er varmestråling viktig i pneumatiske systemer?
- Konklusjon
- Vanlige spørsmål om varmeoverføring i pneumatiske systemer
Beregning av konduksjonskoeffisient: Hvordan beveger varmen seg gjennom komponentene dine?
Konduksjon er den primære varmeoverføringsmekanismen i faste pneumatiske komponenter. Det er viktig å forstå hvordan man beregner og optimaliserer ledningskoeffisientene for å kunne styre systemtemperaturene.
Varmeledningskoeffisienten kan beregnes ved hjelp av Fouriers lov1: q = -k(dT/dx), der q er varmestrømmen (W/m²), k er varmeledningsevnen (W/m-K) og dT/dx er temperaturgradienten. For pneumatiske komponenter avhenger effektiv varmeledning av materialvalg, grensesnittkvalitet og geometriske faktorer som påvirker varmebanelengde og tverrsnittsareal.
Jeg husker en feilsøking på en produksjonslinje i Tennessee der de stangløse sylinderlagrene sviktet for tidlig. Vedlikeholdsteamet hadde prøvd flere smøremidler uten å lykkes. Da vi analyserte ledningsveiene, oppdaget vi en termisk flaskehals ved grensesnittet mellom lager og lagerhus. Ved å forbedre overflatefinishen og påføre en varmeledende forbindelse økte vi den effektive ledningskoeffisienten med 340% og eliminerte feilene fullstendig.
Grunnleggende konduksjonsligninger
La oss se nærmere på de viktigste ligningene for beregning av ledningsevne i pneumatiske komponenter:
Fouriers lov for varmeledning
Den grunnleggende ligningen som styrer varmeledning er:
q = -k(dT/dx)
Hvor?
- q = Varmestrøm (W/m²)
- k = Varmeledningsevne (W/m-K)
- dT/dx = Temperaturgradient (K/m)
For et enkelt endimensjonalt tilfelle med konstant tverrsnitt:
Q = kA(T₁-T₂)/L
Hvor?
- Q = Varmeoverføringshastighet (W)
- A = Tverrsnittsareal (m²)
- T₁, T₂ = Temperaturer i hver ende (K)
- L = lengden på varmebanen (m)
Konseptet termisk motstand
For komplekse geometrier er metoden med termisk motstand ofte mer praktisk:
R = L/(kA)
Hvor?
- R = Termisk motstand (K/W)
For systemer med flere komponenter i serie:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
Og varmeoverføringshastigheten blir:
Q = ΔT/Rtotal
Sammenligning av materialers varmeledningsevne
| Materiale | Varmeledningsevne (W/m-K) | Relativ konduktivitet | Vanlige bruksområder |
|---|---|---|---|
| Aluminium | 205-250 | Høy | Sylindere, kjøleribber |
| Stål | 36-54 | Medium | Strukturelle komponenter |
| Rustfritt stål | 14-16 | Lav-middels | Korrosive miljøer |
| Bronse | 26-50 | Medium | Lagre, gjennomføringer |
| PTFE | 0.25 | Svært lav | Tetninger, lagre |
| Nitrilgummi | 0.13 | Svært lav | O-ringer, tetninger |
| Luft (fortsatt) | 0.026 | Ekstremt lav | Fyllstoff for hull |
| Termisk pasta | 3-8 | Lav | Grensesnittmateriale |
Kontaktmotstand i pneumatiske sammenstillinger
I grensesnitt mellom komponenter påvirker kontaktmotstanden varmeoverføringen betydelig:
Rcontact = 1/(hc × A)
Hvor?
- hc = Kontaktkoeffisient (W/m²-K)
- A = Kontaktareal (m²)
Faktorer som påvirker kontaktmotstanden er blant annet
- Overflateruhet: Ruere overflater har mindre faktisk kontaktflate
- Kontakt Trykk: Høyere trykk øker det effektive kontaktområdet
- Grensesnittmaterialer: Termiske forbindelser fyller luftspalter
- Overflatens renhet: Forurensninger kan øke resistensen
Casestudie: Termisk optimalisering av stangløse sylindere
For en magnetisk sylinder uten stang som opplever termiske problemer:
| Komponent | Opprinnelig design | Optimalisert design | Forbedring |
|---|---|---|---|
| Sylinderhus | Anodisert aluminium | Samme materiale, forbedret finish | 15% bedre ledning |
| Grensesnitt for lager | Metall-mot-metall-kontakt | Tilsatt termisk forbindelse | 340% bedre ledning |
| Monteringsbraketter | Lakkert stål | Bare aluminium | 280% bedre ledning |
| Samlet termisk motstand | 2,8 K/W | 0,7 K/W | 75% reduksjon |
| Driftstemperatur | 78°C | 56°C | 22 °C reduksjon |
| Komponentens levetid | 4 måneder | >12 måneder | 3× forbedring |
Praktiske konduksjonsoptimaliseringsteknikker
Basert på min erfaring med hundrevis av pneumatiske systemer, er dette de mest effektive metodene for å forbedre ledningen:
Optimalisering av grensesnitt
- Overflatebehandling: Forbedre kontaktflatens glatthet til Ra 0,4-0,8 μm
- Materialer for termiske grensesnitt2: Påfør passende forbindelser (3-8 W/m-K)
- Dreiemoment for festemidler: Sørg for riktig stramming for optimalt kontakttrykk
- Renslighet: Fjern alle oljer og forurensninger før montering
Strategier for materialvalg
- Kritiske varmebaner: Bruk materialer med høy ledningsevne (aluminium, kobber)
- Termiske pauser: Bruk bevisst materialer med lav ledningsevne for å isolere varmen
- Sammensatte tilnærminger: Kombiner materialer for optimal ytelse/kostnad
- Anisotropiske materialer: Bruk retningsbestemt konduktivitet der det er hensiktsmessig
Geometrisk optimalisering
- Lengde på varmebane: Minimer avstanden mellom varmekilder og kjøleribber
- Tverrsnittsareal: Maksimer arealet vinkelrett på varmestrømmen
- Termiske flaskehalser: Identifiser og eliminer innsnevringer i varmebanen
- Overflødige stier: Opprett flere parallelle ledningsveier
Metoder for forbedring av konveksjon: Hvilke teknikker maksimerer luft-til-overflate-varmeoverføring?
Konveksjon er ofte den begrensende faktoren når det gjelder kjøling av pneumatiske systemer. Ved å forbedre konvektiv varmeoverføring kan man dramatisk forbedre den termiske styringen og systemets ytelse.
Konvektiv varmeoverføring følger Newtons lov om avkjøling3: Q = hA(Ts-T∞), der h er konveksjonskoeffisienten (W/m²-K), A er overflatearealet, og (Ts-T∞) er temperaturforskjellen mellom overflaten og væsken. Forbedringsmetodene omfatter blant annet å øke overflatearealet ved hjelp av lameller, forbedre væskehastigheten ved hjelp av styrt luftstrøm og optimalisere overflateegenskapene for å fremme turbulente grenselag.
Under en energieffektivitetsrevisjon på et emballasjeanlegg i Arizona oppdaget jeg et pneumatisk system som ble drevet i omgivelser på 43 °C. De stangløse sylindrene ble overopphetet til tross for at de oppfylte alle vedlikeholdskrav. Ved å implementere målrettet konveksjonsforbedring - ved å legge til små aluminiumsfinner og en vifte med lavt strømforbruk - økte vi konveksjonskoeffisienten med 450%. Dette reduserte driftstemperaturene fra farlige nivåer til innenfor spesifikasjonene, uten noen større systemendringer.
Grunnleggende om konveksjon og varmeoverføring
Den grunnleggende ligningen som styrer konvektiv varmeoverføring er
Q = hA(Ts-T∞)
Hvor?
- Q = Varmeoverføringshastighet (W)
- h = konveksjonskoeffisient (W/m²-K)
- A = Overflateareal (m²)
- Ts = overflatetemperatur (K)
- T∞ = Væskens (luftens) temperatur (K)
Konveksjonskoeffisienten h avhenger av flere faktorer:
- Væskeegenskaper (tetthet, viskositet, varmeledningsevne)
- Strømningsegenskaper (hastighet, turbulens)
- Overflategeometri og orientering
- Strømningsregime (naturlig vs. tvungen konveksjon)
Naturlig vs. tvungen konveksjon
| Parameter | Naturlig konveksjon | Tvangskonveksjon | Konsekvenser |
|---|---|---|---|
| Typisk h-verdi | 5-25 W/m²-K | 25-250 W/m²-K | Tvangskonveksjon kan være 10 ganger mer effektivt |
| Drivkraft | Oppdrift (temperaturforskjell) | Eksternt trykk (vifter, blåsere) | Tvangskonveksjon er mindre avhengig av temperaturen |
| Flytmønster | Vertikal strømning langs overflater | Retningsbestemt basert på pådrivningsmekanisme | Tvangsstrømning kan optimaliseres for spesifikke komponenter |
| Pålitelighet | Passiv, alltid til stede | Krever strøm og vedlikehold | Naturlig konveksjon gir grunnleggende kjøling |
| Plassbehov | Krever klaring for luftsirkulasjon | Krever plass til luftventilatorer og kanaler | Tvungne systemer trenger mer planlegging |
Teknikker for forbedring av konveksjon
Forstørrelse av overflateareal
Øker det effektive overflatearealet gjennom:
Finner og forlengede overflater
- Pin finner: Omnidireksjonell luftstrøm, 150-300% arealøkning
- Platefinner: Retningsbestemt luftstrøm, 200-500% arealøkning
- Korrugerte overflater: Moderat forbedring, 50-150% arealøkningOpprugging av overflaten
- Mikroteksturering: 5-15% effektiv arealøkning
- Dimplede overflater: 10-30%-økning pluss grenselagseffekter
- Rillede mønstre: 15-40% øker med retningsbestemte fordeler
Flytmanipulering
Forbedring av luftstrømningsegenskapene gjennom:
Tvangsluftsystemer
- Vifter: Retningsstyrt luftstrøm, 200-600% h forbedring
- Blåsere: Høytrykksblåsere, 300-800% h forbedring
- Trykkluftstråler: Målrettet kjøling, 400-1000% lokal h forbedringOptimalisering av strømningsveier
- Baffler: Direkte luft til kritiske komponenter
- Venturi-effekter: Luften akselererer over bestemte overflater
- Virvelgeneratorer: Skaper turbulens for å forstyrre grenselaget
Modifikasjoner på overflaten
Endring av overflateegenskaper for å forbedre konveksjonen:
Emissivitetsbehandlinger
- Svart oksid: Øker emissiviteten til 0,7-0,9
- Anodisering: Kontrollert emissivitet fra 0,4-0,9
- Maling og belegg: Tilpassbar emissivitet på opptil 0,98Kontroll av fuktbarhet
- Hydrofile belegg: Forbedrer væskekjøling
- Hydrofobe overflater: Forhindrer kondensproblemer
- Mønstret fuktbarhet: Styrt kondensatstrøm
Eksempel på praktisk implementering
For en stangløs pneumatisk sylinder som brukes i omgivelser med høy temperatur:
| Forbedringsmetode | Implementering | h Forbedring | Temperaturreduksjon |
|---|---|---|---|
| Pin Fins (6 mm) | Aluminiumsfinner som klipses på, 10 mm avstand | 180% | 12°C |
| Rettet luftstrøm | 80 mm, 2 W likestrømsvifte ved 1,5 m/s | 320% | 18°C |
| Overflatebehandling | Svart anodisering | 40% | 3°C |
| Kombinert tilnærming | Alle metoder integrert | 450% | 24°C |
Nusseltall-korrelasjon for designberegninger
For tekniske beregninger skal Nusselt-tall4 (Nu) gir en dimensjonsløs tilnærming til konveksjon:
Nu = hL/k
Hvor?
- L = Karakteristisk lengde
- k = Væskens varmeledningsevne
For tvungen konveksjon over en flat plate:
Nu = 0,664Re^(1/2)Pr^(1/3) (laminær strømning)
Nu = 0,037Re^(4/5)Pr^(1/3) (turbulent strømning)
Hvor?
- Re = Reynolds tall (hastighet × lengde × tetthet / viskositet)
- Pr = Prandtl-tall (spesifikk varme × viskositet / varmeledningsevne)
Disse korrelasjonene gjør det mulig for ingeniører å forutsi konveksjonskoeffisienter for ulike konfigurasjoner og optimalisere kjølestrategier deretter.
Modell for strålingseffektivitet: Når er varmestråling viktig i pneumatiske systemer?
Stråling blir ofte oversett i forbindelse med varmestyring av pneumatiske systemer, men den kan stå for 15-30% av den totale varmeoverføringen i mange bruksområder. Å forstå når og hvordan man kan optimalisere strålingsvarmeoverføringen, er avgjørende for omfattende varmestyring.
Strålingsvarmeoverføring følger Stefan-Boltzmanns lov5: Q = εσA(T₁⁴-T₂⁴), der ε er overflatens emissivitet, σ er Stefan-Boltzmann-konstanten, A er overflatearealet, og T₁ og T₂ er absolutte temperaturer på den emitterende overflaten og omgivelsene. Strålingseffektiviteten i pneumatiske systemer avhenger først og fremst av overflatens emissivitet, temperaturdifferansen og visningsfaktorer mellom komponentene og omgivelsene.
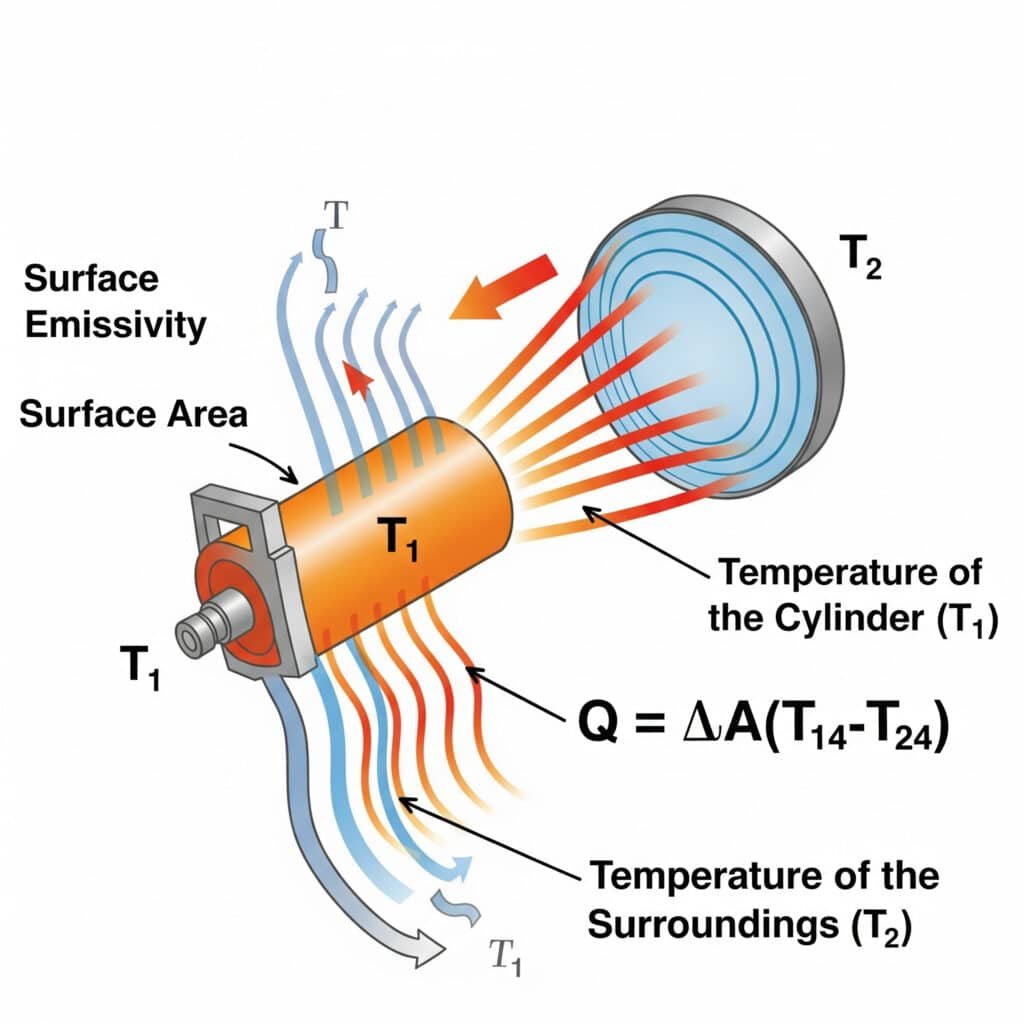
Jeg hjalp nylig en produsent av halvlederutstyr i Oregon med å løse problemer med overoppheting av deres presisjonssylindere uten stenger. Ingeniørene deres hadde utelukkende fokusert på ledning og konveksjon, men hadde oversett stråling. Ved å påføre et belegg med høy emissivitet (ε økte fra 0,11 til 0,92), forbedret vi strålingsvarmeoverføringen med over 700%. Denne enkle, passive løsningen reduserte driftstemperaturen med 9 °C uten bevegelige deler eller energiforbruk - et kritisk krav i deres renromsmiljø.
Grunnleggende om varmeoverføring ved stråling
Den grunnleggende ligningen som styrer strålingsvarmeoverføring er
Q = εσA(T₁⁴-T₂⁴)
Hvor?
- Q = Varmeoverføringshastighet (W)
- ε = Emissivitet (dimensjonsløs, 0-1)
- σ = Stefan-Boltzmann-konstant (5,67 × 10-⁸ W/m²-K⁴)
- A = Overflateareal (m²)
- T₁ = Overflatens absolutte temperatur (K)
- T₂ = omgivelsenes absolutte temperatur (K)
Overflateemissivitetsverdier for vanlige pneumatiske materialer
| Materiale/overflate | Emissivitet (ε) | Strålingseffektivitet | Forbedringspotensial |
|---|---|---|---|
| Polert aluminium | 0.04-0.06 | Svært dårlig | >1500% forbedring mulig |
| Anodisert aluminium | 0.7-0.9 | Utmerket | Allerede optimalisert |
| Rustfritt stål (polert) | 0.07-0.14 | Dårlig | >600% forbedring mulig |
| Rustfritt stål (oksidert) | 0.6-0.85 | Bra | Moderat forbedring mulig |
| Stål (polert) | 0.07-0.10 | Dårlig | >900% forbedring mulig |
| Stål (oksidert) | 0.7-0.9 | Utmerket | Allerede optimalisert |
| Malte overflater | 0.8-0.98 | Utmerket | Allerede optimalisert |
| PTFE (hvit) | 0.8-0.9 | Utmerket | Allerede optimalisert |
| Nitrilgummi | 0.86-0.94 | Utmerket | Allerede optimalisert |
Vis faktorbetraktninger
Strålingsutveksling avhenger ikke bare av emissivitet, men også av geometriske forhold mellom overflater:
F₁₂ = Andel av strålingen som går fra overflate 1 og treffer overflate 2
For komplekse geometrier kan visningsfaktorer beregnes ved hjelp av:
- Analytiske løsninger for enkle geometrier
- Vis faktoralgebra for å kombinere kjente løsninger
- Numeriske metoder for komplekse arrangementer
- Empiriske tilnærminger for praktisk ingeniørarbeid
Temperaturavhengighet av stråling
Temperaturforholdet med fjerde potens gjør stråling spesielt effektiv ved høyere temperaturer:
| Overflatetemperatur | Prosentandel av varmeoverføring ved hjelp av stråling*. |
|---|---|
| 30 °C (303 K) | 5-15% |
| 50 °C (323 K) | 10-25% |
| 75 °C (348 K) | 15-35% |
| 100 °C (373 K) | 25-45% |
| 150 °C (423 K) | 35-60% |
*Forutsatt naturlig konveksjon, ε = 0,8, 25 °C omgivelsestemperatur
Strategier for å forbedre strålingseffektiviteten
Basert på min erfaring med industrielle pneumatiske systemer er dette de mest effektive metodene for å forbedre strålingsvarmeoverføringen:
Modifisering av overflateemissivitet
Belegg med høy emissivitet
- Svart anodisering for aluminium (ε ≈ 0,8-0,9)
- Svart oksid for stål (ε ≈ 0,7-0,8)
- Keramiske spesialbelegg (ε ≈ 0,9-0,98)Teksturering av overflater
- Mikroruhet øker den effektive emissiviteten
- Porøse overflater forbedrer strålingsegenskapene
- Kombinert emissivitet/konveksjon
Miljømessig optimalisering
Styring av omgivelsestemperatur
- Skjerming mot varmt utstyr/varme prosesser
- Kjølige vegger/tak for bedre strålingsutveksling
- Reflekterende barrierer for å lede strålingen til kjøligere overflaterVis faktorforbedring
- Orientering for å maksimere eksponeringen mot kjølige overflater
- Fjerning av blokkerende gjenstander
- Reflektorer for å forbedre strålingsutvekslingen med kjøligere områder
Casestudie: Forbedring av stråling i presisjonspneumatikk
For en stangløs sylinder med høy presisjon i et renromsmiljø:
| Parameter | Opprinnelig design | Strålingsforbedret design | Forbedring |
|---|---|---|---|
| Overflatemateriale | Polert aluminium (ε ≈ 0,06) | Keramisk belagt aluminium (ε ≈ 0,94) | 1467% økning i emissivitet |
| Strålingsvarmeoverføring | 2.1W | 32.7W | 1457% økning i stråling |
| Driftstemperatur | 68°C | 59°C | 9 °C reduksjon |
| Komponentens levetid | 8 måneder | >24 måneder | 3× forbedring |
| Implementeringskostnader | – | $175 per sylinder | 4,2 måneders tilbakebetaling |
Stråling vs. andre varmeoverføringsmetoder
Å forstå når stråling dominerer, er avgjørende for effektiv varmestyring:
| Tilstand | Ledningsdominans | Konveksjonens dominans | Strålingsdominans |
|---|---|---|---|
| Temperaturområde | Lav til høy | Lav til middels | Middels til høy |
| Materialegenskaper | Materialer med høy k | Lav k, høyt overflateareal | Høye ε-overflater |
| Miljømessige faktorer | God termisk kontakt | Luft i bevegelse, vifter | Stor temperaturdifferanse |
| Plassbegrensninger | Tett emballasje | Åpen luftstrøm | Utsikt til kjøligere omgivelser |
| Beste bruksområder | Grensesnitt for komponenter | Generell kjøling | Varme overflater, vakuum, stillestående luft |
Konklusjon
Beherskelse av varmeoverføringsprinsipper - beregning av ledningskoeffisient, metoder for konveksjonsforbedring og modellering av strålingseffektivitet - danner grunnlaget for effektiv varmestyring i pneumatiske systemer. Ved å bruke disse prinsippene kan du redusere driftstemperaturene, forlenge komponentenes levetid og forbedre energieffektiviteten, samtidig som du sikrer pålitelig drift selv i utfordrende miljøer.
Vanlige spørsmål om varmeoverføring i pneumatiske systemer
Hva er den typiske temperaturstigningen i pneumatiske sylindere under drift?
Pneumatiske sylindere opplever vanligvis temperaturstigninger på 20-40 °C over omgivelsestemperaturen under kontinuerlig drift. Denne økningen skyldes friksjon mellom tetninger og sylindervegger, kompresjonsoppvarming av luft og mekanisk arbeid som omdannes til varme. Sylindere uten stang opplever ofte høyere temperaturstigninger (30-50 °C) på grunn av de mer komplekse tetningssystemene og konsentrert varmeutvikling i lager/tetningsenheten.
Hvordan påvirker driftstrykket varmeutviklingen i pneumatiske systemer?
Driftstrykket har en betydelig innvirkning på varmeutviklingen, og høyere trykk skaper mer varme gjennom flere mekanismer. Hver økning på 1 bar i driftstrykk øker vanligvis varmeutviklingen med 8-12% på grunn av større friksjonskrefter mellom tetninger og overflater, høyere kompresjonsoppvarming og økte lekkasjerelaterte tap. Dette forholdet er tilnærmet lineært innenfor normale driftsområder (3-10 bar).
Hva er den optimale kjølemetoden for pneumatiske komponenter i ulike miljøer?
Den optimale kjølemetoden varierer fra miljø til miljø: I rene omgivelser med moderat temperatur (15-30 °C) er det ofte tilstrekkelig med naturlig konveksjon og riktig komponentavstand. I miljøer med høy temperatur (30-50 °C) er det nødvendig med tvungen konveksjon ved hjelp av vifter eller trykkluft. I ekstremt varme omgivelser (>50 °C) eller der luftstrømmen er begrenset, kan det være nødvendig med aktive kjølemetoder som termoelektriske kjølere eller væskekjøling. I alle tilfeller gir maksimering av stråling gjennom overflater med høy emissivitet ytterligere passiv kjøling.
Hvordan beregner jeg den totale varmeoverføringen fra en pneumatisk komponent?
Beregn den totale varmeoverføringen ved å summere bidragene fra hver mekanisme: Qtotal = Qledning + Qkonveksjon + Qstråling. For ledning bruker du Q = kA(T₁-T₂)/L for hver varmebane. For konveksjon bruker du Q = hA(Ts-T∞) med passende konveksjonskoeffisienter. For stråling brukes Q = εσA(T₁⁴-T₂⁴). I de fleste industrielle pneumatiske applikasjoner som opererer ved 30-80 °C, er den omtrentlige fordelingen 20-40% konduksjon, 40-70% konveksjon og 10-30% stråling.
Hva er forholdet mellom temperatur og levetid på pneumatiske komponenter?
Levetiden til komponentene reduseres eksponentielt med økende temperatur, i henhold til en modifisert Arrhenius-sammenheng. Som en tommelfingerregel kan man si at hver 10 °C økning i driftstemperaturen reduserer levetiden til tetninger og komponenter med 40-50%. Dette betyr at en komponent som fungerer ved 70 °C, kanskje bare varer en tredjedel så lenge som den samme komponenten ved 50 °C. Dette forholdet er spesielt kritisk for polymerkomponenter som tetninger, lagre og pakninger, som ofte bestemmer vedlikeholdsintervallet for pneumatiske systemer.
-
Gir en grunnleggende forklaring av Fouriers lov, det fundamentale prinsippet som beskriver hvordan varme ledes gjennom faste materialer basert på deres varmeledningsevne og temperaturgradient. ↩
-
Forklarer funksjonen til og typene av TIM-materialer (Thermal Interface Materials), som brukes til å fylle mikroskopiske luftspalter mellom komponenter for å forbedre varmeledningen og redusere termisk motstand. ↩
-
Beskriver prinsippene i Newtons kjøleprinsipp, som styrer hvordan objekter kjøles ned ved å overføre varme til den omkringliggende væsken via konveksjon, en nøkkelfaktor i utformingen av kjølesystemer. ↩
-
Gir en grundig innføring i Nusselt-tallet, en kritisk dimensjonsløs størrelse innen væskedynamikk og varmeoverføring som representerer forholdet mellom konvektiv og konduktiv varmeoverføring over en grenseflate. ↩
-
Beskriver Stefan-Boltzmanns lov, det grunnleggende fysiske prinsippet som kvantifiserer den totale energien som utstråles fra et svart legeme, og som er avgjørende for å beregne varmetap fra varme overflater. ↩



