Alle vedlikeholdsingeniørers mareritt er uventet utstyrssvikt. Når maskiner vibrerer med sin egenfrekvens, kan det oppstå katastrofale skader i løpet av minutter. Jeg har sett at dette problemet koster bedrifter tusenvis av kroner i nedetid.
Vibrasjonsresonans1 oppstår når en ytre kraft samsvarer med et systems egenfrekvens, noe som fører til forsterkede svingninger som kan skade utstyret. Å forstå og kontrollere dette fenomenet er avgjørende for å forebygge feil og forlenge maskinens levetid.
La meg dele en kort historie. I fjor ringte en kunde fra Tyskland meg i panikk. Produksjonslinjen deres hadde stoppet opp fordi en stangløs sylinder vibrerte voldsomt. Hva var problemet? Resonans. Når du leser denne artikkelen, vil du forstå hvordan du kan identifisere og forebygge lignende problemer i systemene dine.
Innholdsfortegnelse
- Formel for naturlig frekvens: Hvordan kan du beregne systemets sårbare punkter?
- Massefjærmodellen: Hvorfor er denne forenklede tilnærmingen så verdifull?
- Optimalisering av dempingsforhold: Hvilke eksperimenter gir de beste resultatene?
- Konklusjon
- Vanlige spørsmål om vibrasjonsresonans
Formel for naturlig frekvens: Hvordan kan du beregne systemets sårbare punkter?
Å forstå utstyrets egenfrekvens er det første skrittet mot å forebygge resonansproblemer. Denne kritiske verdien avgjør når systemet er mest utsatt for vibrasjonsproblemer.
Den egenfrekvens2 (fn) for et system kan beregnes ved hjelp av formelen: fn = (1/2π) × √(k/m), der k er stivhetskoeffisienten og m er massen. Denne beregningen avslører frekvensen som systemet ditt vil resonere ved hvis det blir påvirket av matchende eksterne krefter.
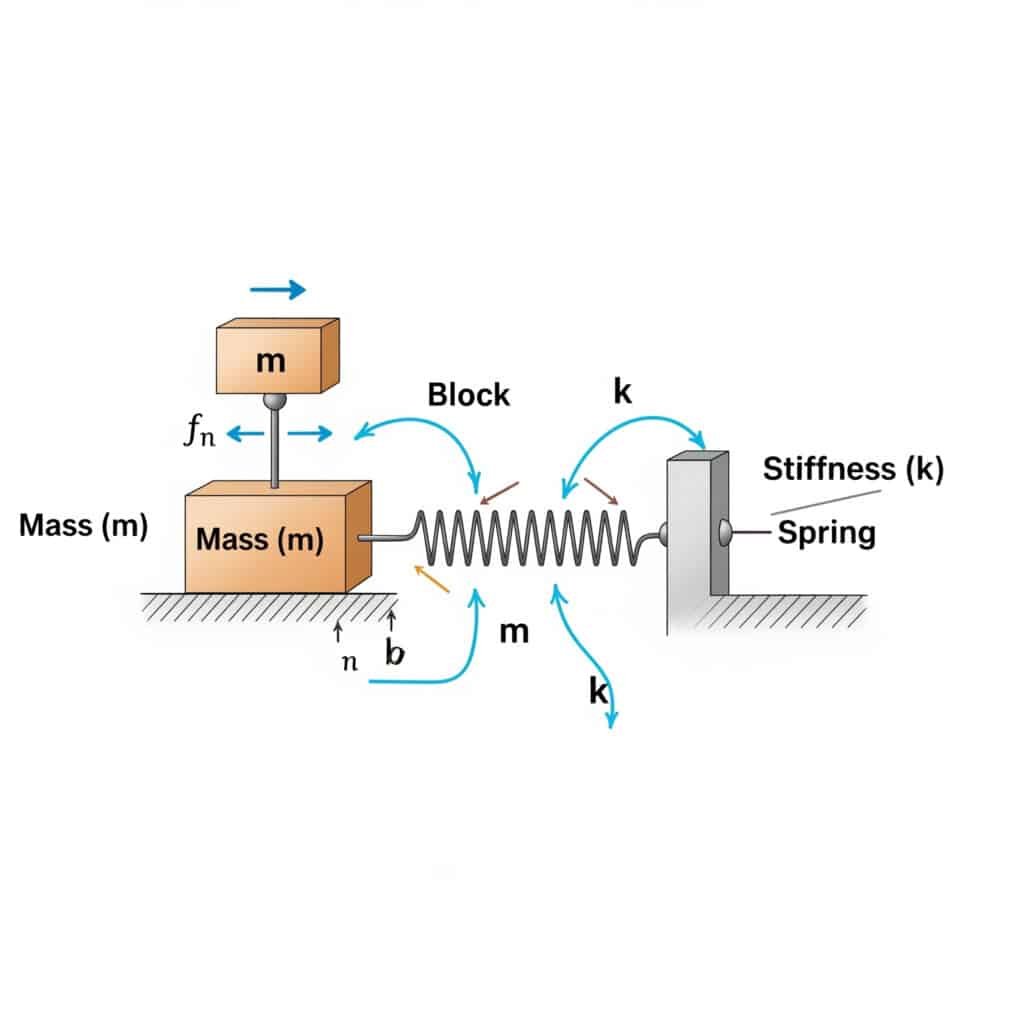
Da jeg besøkte et produksjonsanlegg i Sveits, la jeg merke til at de stangløse pneumatiske sylindrene deres sviktet for tidlig. Vedlikeholdsteamet hadde ikke beregnet anleggets egenfrekvens. Etter å ha brukt denne formelen fant vi ut at driftshastigheten lå farlig nær systemets egenfrekvens.
Praktiske anvendelser av egenfrekvensberegninger
Formelen for egenfrekvens er ikke bare teoretisk - den har direkte anvendelser i ulike industrielle miljøer:
- Valg av utstyr: Velge komponenter med egenfrekvenser som ligger langt unna driftsforholdene dine
- Forebyggende vedlikehold: Planlegging av inspeksjoner basert på vibrasjonsrisikoprofiler
- Feilsøking: Identifisere årsaken til uventede vibrasjoner
Vanlige egenfrekvensverdier for industrikomponenter
| Komponent | Typisk naturlig frekvensområde (Hz) |
|---|---|
| Sylindere uten stang | 10-50 Hz |
| Monteringsbraketter | 20-100 Hz |
| Støttestrukturer | 5-30 Hz |
| Reguleringsventiler | 40-200 Hz |
Kritiske faktorer som påvirker egenfrekvensen
Beregningen av egenfrekvensen virker enkel, men flere faktorer kan komplisere den praktiske anvendelsen:
- Ikke-uniform massefordeling: De fleste industrikomponenter har ikke perfekt fordelt masse
- Variabel stivhet: Komponenter kan ha forskjellig stivhet i ulike retninger
- Tilkoblingspunkter: Hvordan komponenter monteres, har stor betydning for vibrasjonsegenskapene deres
- Temperaturpåvirkning: Både masse- og stivhetsegenskaper kan endre seg med temperaturen
Massefjærmodellen: Hvorfor er denne forenklede tilnærmingen så verdifull?
Masse-fjær-modellen gir et intuitivt rammeverk for å forstå komplekse vibrasjonssystemer. Den reduserer kompliserte maskiner til grunnleggende elementer som ingeniører enkelt kan analysere.
Den masse-fjær-modell3 forenkler vibrasjonsanalyse ved å representere mekaniske systemer som diskrete masser forbundet med fjærer. Denne tilnærmingen gjør det mulig for ingeniører å forutsi systemets oppførsel, identifisere potensielle resonansproblemer og utvikle effektive løsninger uten komplisert matematikk.
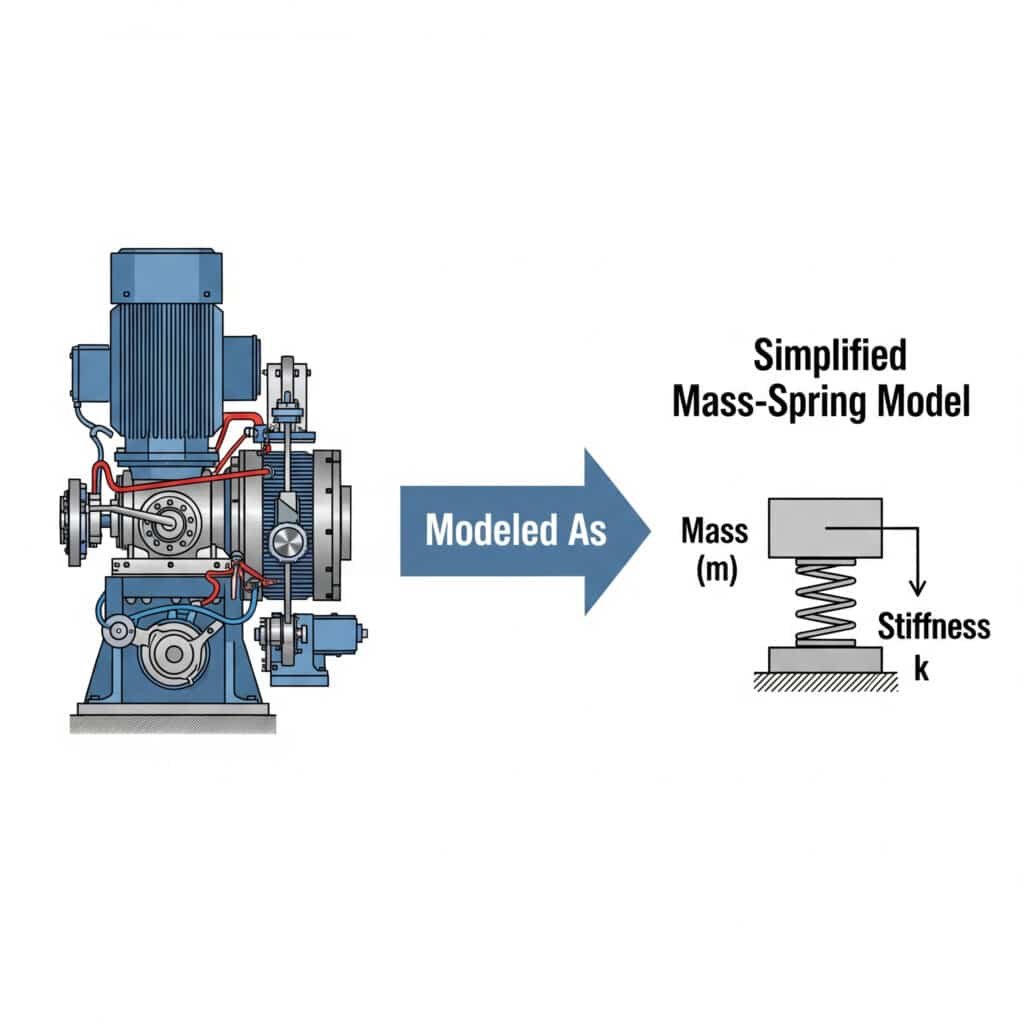
Jeg husker at jeg jobbet med en bildelprodusent i Michigan som ikke kunne forstå hvorfor de styrte, stangløse sylindrene deres sviktet. Ved å modellere systemet som et enkelt masse-fjær-arrangement fant vi ut at monteringsbrakettene fungerte som utilsiktede fjærer, noe som skapte en resonanstilstand.
Konvertering av virkelige systemer til massefjærmodeller
For å bruke denne tilnærmingen på utstyret ditt:
- Identifiser de viktigste massene: Bestem hvilke komponenter som bidrar med betydelig vekt
- Finn fjærelementene: Finn komponenter som lagrer og frigjør energi (faktiske fjærer, fleksible fester osv.)
- Kartforbindelser: Dokumenter hvordan masser og fjærer samvirker
- Forenkle: Kombiner lignende elementer for å skape en håndterbar modell
Typer av massefjærsystemer
| Systemtype | Beskrivelse | Vanlige bruksområder |
|---|---|---|
| Enkelt DOF | Én masse med én fjær | Enkle pneumatiske sylindere |
| Multi-DOF | Flere masser med flere fjærer | Komplekse maskiner med flere komponenter |
| Kontinuerlig | Uendelig DOF (krever annen analyse) | Bjelker, plater og skall |
Avanserte modelleringshensyn
Selv om den grunnleggende massefjærmodellen er verdifull, er det flere forbedringer som gjør den mer realistisk:
- Legge til dempere: Reelle systemer har alltid energitap
- Tatt i betraktning ikke-lineariteter: Fjærene følger ikke alltid Hookes lov4 perfekt
- Regnskap for tvungen vibrasjon: Eksterne krefter endrer systemets atferd
- Inkludert koblingseffekter: Bevegelse i én retning kan påvirke andre retninger
Optimalisering av dempingsforhold: Hvilke eksperimenter gir de beste resultatene?
Demping er det beste forsvaret mot resonansproblemer. Ved å finne det optimale dempingsforholdet gjennom eksperimentering kan du forbedre systemets ytelse og pålitelighet dramatisk.
Dempingsforhold5 Optimaliseringseksperimenter innebærer systematisk testing av ulike dempingskonfigurasjoner for å finne den ideelle balansen mellom vibrasjonskontroll og systemrespons. Det optimale dempingsforholdet ligger vanligvis mellom 0,2 og 0,7, noe som gir tilstrekkelig vibrasjonsdemping uten for stort energitap.
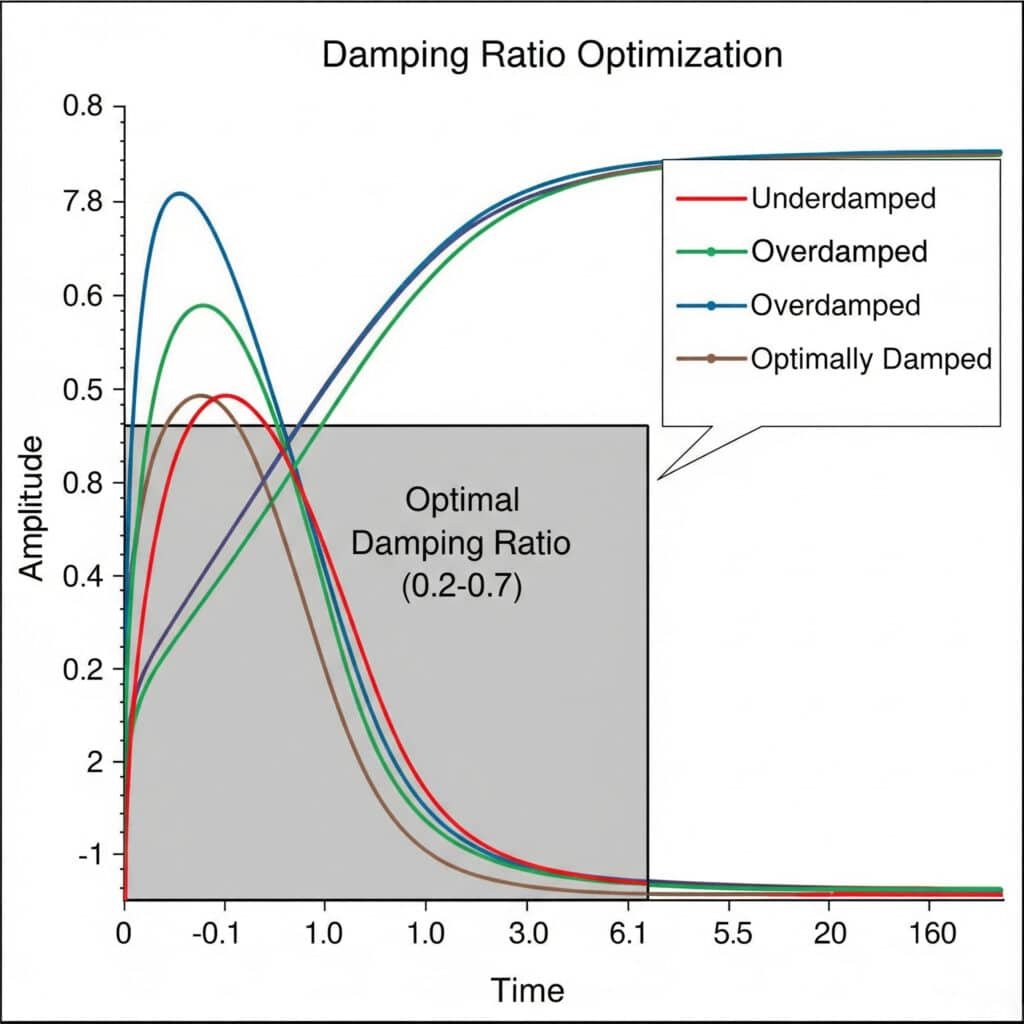
I forrige måned hjalp jeg en fransk produsent av næringsmiddelutstyr med å løse vedvarende vibrasjonsproblemer i de magnetiske sylindrene uten stenger. Gjennom en rekke eksperimenter med dempingsforhold oppdaget vi at den opprinnelige konstruksjonen hadde et dempingsforhold på bare 0,05 - alt for lavt til å forhindre resonansproblemer.
Eksperimentelt oppsett for testing av dempingsforhold
For å gjennomføre effektive eksperimenter med optimalisering av demping:
- Grunnlinjemåling: Registrer systemrespons uten ekstra demping
- Inkrementell testing: Legg til dempingselementer i kontrollerte trinn
- Måling av respons: Måle amplitude, stabiliseringstid og frekvensrespons
- Analyse av data: Beregn dempingsforholdet for hver konfigurasjon
- Validering: Verifiser ytelsen under faktiske driftsforhold
Sammenligning av dempingsteknologier
| Dempingsteknologi | Fordeler | Begrensninger | Typiske bruksområder |
|---|---|---|---|
| Viskøse spjeld | Forutsigbar ytelse, temperaturstabil | Krever vedlikehold, potensielle lekkasjer | Tunge maskiner, presisjonsutstyr |
| Friksjonsdempere | Enkel design, kostnadseffektivt | Slitasje over tid, ikke-lineær oppførsel | Strukturelle støtter, grunnleggende maskineri |
| Materialdemping | Ingen bevegelige deler, kompakt | Begrenset justeringsområde | Presisjonsinstrumenter, vibrasjonsisolering |
| Aktiv demping | Tilpasningsdyktig til skiftende forhold | Kompleks, krever strøm | Kritiske bruksområder, utstyr med variabel hastighet |
Optimalisering av demping for ulike driftsforhold
Det ideelle dempingsforholdet er ikke universelt - det avhenger av det spesifikke bruksområdet:
- Operasjoner med høy hastighet: Lavere dempingsforhold (0,1-0,3) opprettholder responsen
- Presisjonsanvendelser: Høyere dempingsforhold (0,5-0,7) gir stabilitet
- Systemer med variabel belastning: Adaptiv demping kan være nødvendig
- Temperaturfølsomme miljøer: Vurder dempematerialer med stabile egenskaper
Casestudie: Optimalisering av demping i stangløse sylindere
Da vi skulle optimalisere en dobbeltvirkende, stangløs sylinder til en pakkemaskin, testet vi fem ulike dempekonfigurasjoner:
- Standard endeputer: Dempingsforhold = 0,12
- Forlengede puter: Dempingsforhold = 0,25
- Utvendige støtdempere: Dempingsforhold = 0,41
- Monteringsbraketter i kompositt: Dempingsforhold = 0,38
- Kombinert tilnærming (3+4): Dempingsforhold = 0,53
Den kombinerte tilnærmingen ga best ytelse, og reduserte vibrasjonsamplituden med 78% samtidig som responstiden var akseptabel.
Konklusjon
Forståelse av vibrasjonsresonans gjennom beregninger av egenfrekvenser, modellering av massefjærer og optimalisering av dempingsforhold er avgjørende for å forebygge feil på utstyret. Ved å bruke disse prinsippene kan du forlenge maskinens levetid, redusere nedetiden og forbedre den generelle systemytelsen.
Vanlige spørsmål om vibrasjonsresonans
Hva er vibrasjonsresonans i industrielt utstyr?
Vibrasjonsresonans oppstår når en ekstern kraft samsvarer med et systems egenfrekvens, noe som forårsaker forsterkede svingninger. I industrielt utstyr kan dette fenomenet føre til overdrevne bevegelser, utmattelse av komponenter og katastrofale feil hvis det ikke håndteres på riktig måte.
Hvordan kan jeg identifisere om systemet mitt opplever resonans?
Se etter symptomer som uforklarlige støyøkninger, synlige vibrasjoner ved bestemte hastigheter, for tidlig svikt i komponenter og ytelsesforringelse som oppstår ved konstante driftspunkter. Vibrasjonsanalyseverktøy kan bekrefte resonansforhold.
Hva er forskjellen mellom tvungen vibrasjon og resonans?
Påtvungne vibrasjoner oppstår når en ytre kraft virker på et system, mens resonans er den spesifikke tilstanden når den påtvungne frekvensen stemmer overens med systemets egenfrekvens, noe som resulterer i forsterket respons. All resonans involverer tvungen vibrasjon, men ikke all tvungen vibrasjon forårsaker resonans.
Hvordan påvirker utformingen av en stangløs pneumatisk sylinder vibrasjonsegenskapene?
Utformingen av stangløse pneumatiske sylindere - med bevegelig vogn, innvendig tetningssystem og styringsmekanismer - skaper unike vibrasjonsutfordringer. Den forlengede profilen fungerer som en bjelke som kan bøye seg, vognens masse skaper treghetskrefter, og tetningsbåndene kan introdusere variabel friksjon.
Hvilke enkle modifikasjoner kan redusere resonansen i eksisterende utstyr?
For eksisterende utstyr som har problemer med resonans, bør du vurdere å tilføre masse for å endre egenfrekvensen, installere eksterne dempere eller støtdempere, endre monteringsmetoder for å inkludere vibrasjonsisolering eller justere driftshastighetene for å unngå resonansfrekvenser.
-
Gir en grunnleggende forklaring på mekanisk resonans, ofte med visuelle eksempler, og demonstrerer hvordan en liten periodisk kraft kan skape svingninger med stor amplitude i et system. ↩
-
Gir en detaljert innføring i fysikken bak egenfrekvensen, den spesifikke frekvensen som et system har en tendens til å svinge ved når det ikke er noen drivende eller dempende kraft til stede. ↩
-
Forklarer prinsippene i masse-fjær-modellen, en grunnleggende idealisering i fysikk og ingeniørfag som brukes til å analysere komplekse systemer som utviser enkel harmonisk bevegelse. ↩
-
Detaljer Hookes lov, et fysikkprinsipp som sier at kraften som trengs for å strekke ut eller komprimere en fjær en viss avstand, er direkte proporsjonal med denne avstanden. ↩
-
Beskriver dempningsforholdet, et dimensjonsløst mål som definerer hvordan svingninger i et system avtar etter en forstyrrelse, noe som er avgjørende for å kontrollere resonans. ↩


