
Sliter du med å forutsi den faktiske ytelsen til den pneumatiske sylinderen din? Mange ingeniører feilberegner kraftuttak og trykkbehov, noe som fører til systemfeil og kostbar nedetid. Men det finnes en enkel måte å mestre disse beregningene på.
Pneumatiske sylindere fungerer i henhold til grunnleggende fysiske prinsipper, først og fremst Pascals lov1, som sier at trykk som påføres en innesluttet væske, overføres likt i alle retninger. Dette gjør at vi kan beregne sylinderkraften ved å multiplisere trykket med det effektive stempelarealet, med strømningshastigheter og trykkenheter som krever presise omregninger for nøyaktig systemdesign.
Jeg har brukt over ti år på å hjelpe kunder med å optimalisere sine pneumatiske systemer, og jeg har sett hvordan forståelsen av disse grunnleggende prinsippene kan forandre systemets pålitelighet. La meg dele den praktiske kunnskapen som vil hjelpe deg å unngå de vanligste feilene jeg ser hver dag.
Innholdsfortegnelse
- Hvordan bestemmer Pascals lov sylinderens kraftutgang?
- Hva er forholdet mellom luftstrøm og trykk i sylindere?
- Hvorfor er det viktig å forstå omregning av trykkenheter for systemdesign?
- Konklusjon
- Vanlige spørsmål om fysikk i pneumatiske systemer
Hvordan bestemmer Pascals lov sylinderens kraftutgang?
Å forstå Pascals lov er grunnleggende for å kunne forutsi og optimalisere sylinderytelsen i ethvert pneumatisk system.
Pascals lov sier at trykket som utøves på en væske i et lukket system, overføres likt i hele væsken. For pneumatiske sylindere betyr dette at kraften som utløses, er lik trykket multiplisert med det effektive stempelarealet (F = P × A). Dette enkle forholdet er grunnlaget for alle sylinderkraftberegninger.

Utledning av kraftberegningen
La oss bryte ned den matematiske utledningen av sylinderkraftberegninger:
Grunnleggende kraftlikning
Den grunnleggende ligningen for sylinderkraft er
F = P × A
Hvor?
- F = utgangskraft (N)
- P = Trykk (Pa)
- A = Effektivt stempelareal (m²)
Hensyn til effektivt område
Det effektive området varierer avhengig av sylindertype og retning:
| Sylindertype | Forlengelsesstyrke | Tilbaketrekkingskraft |
|---|---|---|
| Enkeltvirkende | P × A | Kun fjærkraft |
| Dobbeltvirkende (standard) | P × A | P × (A - a) |
| Dobbeltvirkende (stangløs) | P × A | P × A |
Hvor?
- A = Hele stempelområdet
- a = stangens tverrsnittsareal
En gang rådførte jeg meg med en produksjonsbedrift i Ohio som opplevde utilstrekkelig kraft i pressapplikasjonen sin. Beregningene deres virket riktige på papiret, men den faktiske ytelsen var mangelfull. Da jeg undersøkte saken, oppdaget jeg at de brukte manometertrykk2 i beregningene i stedet for absolutt trykk, og de hadde ikke tatt hensyn til stangarealet under tilbaketrekking. Etter å ha gjort nye beregninger med riktig formel og riktige trykkverdier, klarte vi å dimensjonere systemet riktig, noe som økte produktiviteten med 23%.
Praktiske eksempler på kraftberegning
La oss se nærmere på noen beregninger fra den virkelige verden:
Eksempel 1: Forlengelseskraft i en standardsylinder
For en sylinder med:
- Borediameter = 50 mm (radius = 25 mm = 0,025 m)
- Driftstrykk = 6 bar (600 000 Pa)
Stempelområdet er:
A = π × r² = π × (0,025)² = 0,001963 m²
Forlengelseskraften er:
F = P × A = 600 000 Pa × 0,001963 m² = 1178 N ≈ 118 kg kraft
Eksempel 2: Tilbaketrekkingskraft i samme sylinder
Hvis stangens diameter er 20 mm (radius = 10 mm = 0,01 m):
Stangområdet er:
a = π × r² = π × (0,01)² = 0,000314 m²
Det effektive tilbaketrekningsområdet er:
A - a = 0,001963 - 0,000314 = 0,001649 m²
Tilbaketrekkingskraften er:
F = P × (A - a) = 600 000 Pa × 0,001649 m² = 989 N ≈ 99 kg kraft
Effektivitetsfaktorer i virkelige applikasjoner
I praktiske anvendelser er det flere faktorer som påvirker den teoretiske kraftberegningen:
Friksjonstap
Friksjon mellom stempeltetningen og sylinderveggen reduserer den effektive kraften:
| Tetningstype | Typisk effektivitetsfaktor |
|---|---|
| Standard NBR | 0.85-0.90 |
| PTFE med lav friksjon | 0.90-0.95 |
| Aldrende/slitte tetninger | 0.70-0.85 |
Praktisk kraftlikning
En mer nøyaktig kraftlikning for den virkelige verden er
F_aktuell = η × P × A
Hvor?
- η (eta) = Effektivitetsfaktor (vanligvis 0,85-0,95)
Hva er forholdet mellom luftstrøm og trykk i sylindere?
Forståelsen av forholdet mellom strømningshastighet og trykk er avgjørende for å kunne dimensjonere lufttilførselssystemer og forutsi sylinderhastigheten.
Luftstrøm og trykk i pneumatiske systemer er omvendt relatert - når trykket øker, synker vanligvis luftstrømmen. Dette forholdet følger gasslovene og påvirkes av restriksjoner, temperatur og systemvolum. Riktig sylinderdrift krever at disse faktorene balanseres for å oppnå ønsket hastighet og kraft.
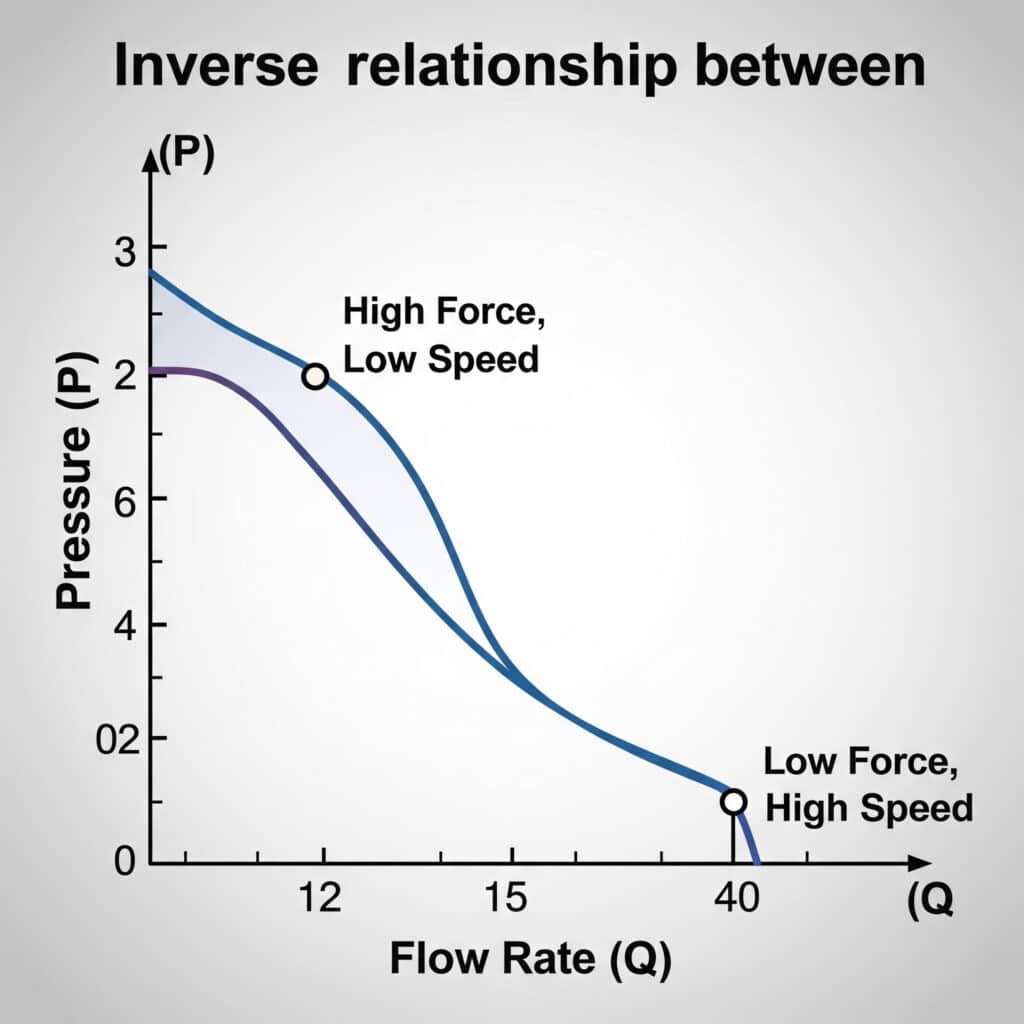
Konverteringstabell for strømning og trykk
Denne praktiske referansetabellen viser forholdet mellom strømningshastighet og trykkfall over ulike systemkomponenter:
| Rørstørrelse (mm) | Strømningshastighet (l/min) | Trykkfall (bar/meter) ved 6 bar tilførsel |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
Matematikk om strømning og trykk
Forholdet mellom strømning og trykk følger flere gasslover:
Poiseuilles ligning3 for laminær strømning
For laminær strømning gjennom rør:
Q = (π × r⁴ × ΔP) / (8 × η × L)
Hvor?
- Q = Volumetrisk strømningshastighet
- r = rørradius
- ΔP = Trykkforskjell
- η = dynamisk viskositet
- L = Rørets lengde
Strømningskoeffisient (Cv)4 Metode
For komponenter som ventiler:
Q = Cv × √ΔP
Hvor?
- Q = Strømningshastighet
- Cv = Strømningskoeffisient
- ΔP = Trykkfall over komponenten
Beregning av sylinderhastighet
Hastigheten til en pneumatisk sylinder avhenger av strømningshastigheten og sylinderarealet:
v = Q / A
Hvor?
- v = Sylinderhastighet (m/s)
- Q = Strømningshastighet (m³/s)
- A = Stempelareal (m²)
Under et prosjekt på et emballasjeanlegg i Frankrike nylig opplevde jeg en situasjon der kundens stangløse sylindere beveget seg for sakte til tross for tilstrekkelig trykk. Ved å analysere systemet deres ved hjelp av våre strømningstrykkberegninger identifiserte vi underdimensjonerte tilførselsledninger som forårsaket et betydelig trykkfall. Etter å ha oppgradert fra 6 mm til 10 mm slanger, ble syklustiden forbedret med 40%, noe som økte produksjonskapasiteten dramatisk.
Kritiske strømningshensyn
Det er flere faktorer som påvirker forholdet mellom strømning og trykk i pneumatiske systemer:
Fenomenet med kvalt strømning5
Når trykkforholdet overskrider en kritisk verdi (ca. 0,53 for luft), blir gjennomstrømningen "kvalt" og kan ikke øke uansett trykkreduksjon nedstrøms.
Temperaturpåvirkning
Strømningshastigheten påvirkes av temperaturen i henhold til forholdet:
Q₂ = Q₁ × √(T₂/T₁)
Hvor?
- Q₁, Q₂ = Strømningshastigheter ved ulike temperaturer
- T₁, T₂ = Absolutte temperaturer
Hvorfor er det viktig å forstå omregning av trykkenheter for systemdesign?
Det er viktig å kunne navigere i de ulike trykkenhetene som brukes over hele verden, for å sikre riktig systemdesign og internasjonal kompatibilitet.
Omregning av trykkenheter er kritisk fordi pneumatiske komponenter og spesifikasjoner bruker ulike enheter avhengig av region og bransje. Feil tolkning av enheter kan føre til betydelige beregningsfeil, med potensielt farlige konsekvenser. Konvertering mellom absolutt-, manometer- og differensialtrykk gjør det enda mer komplisert.
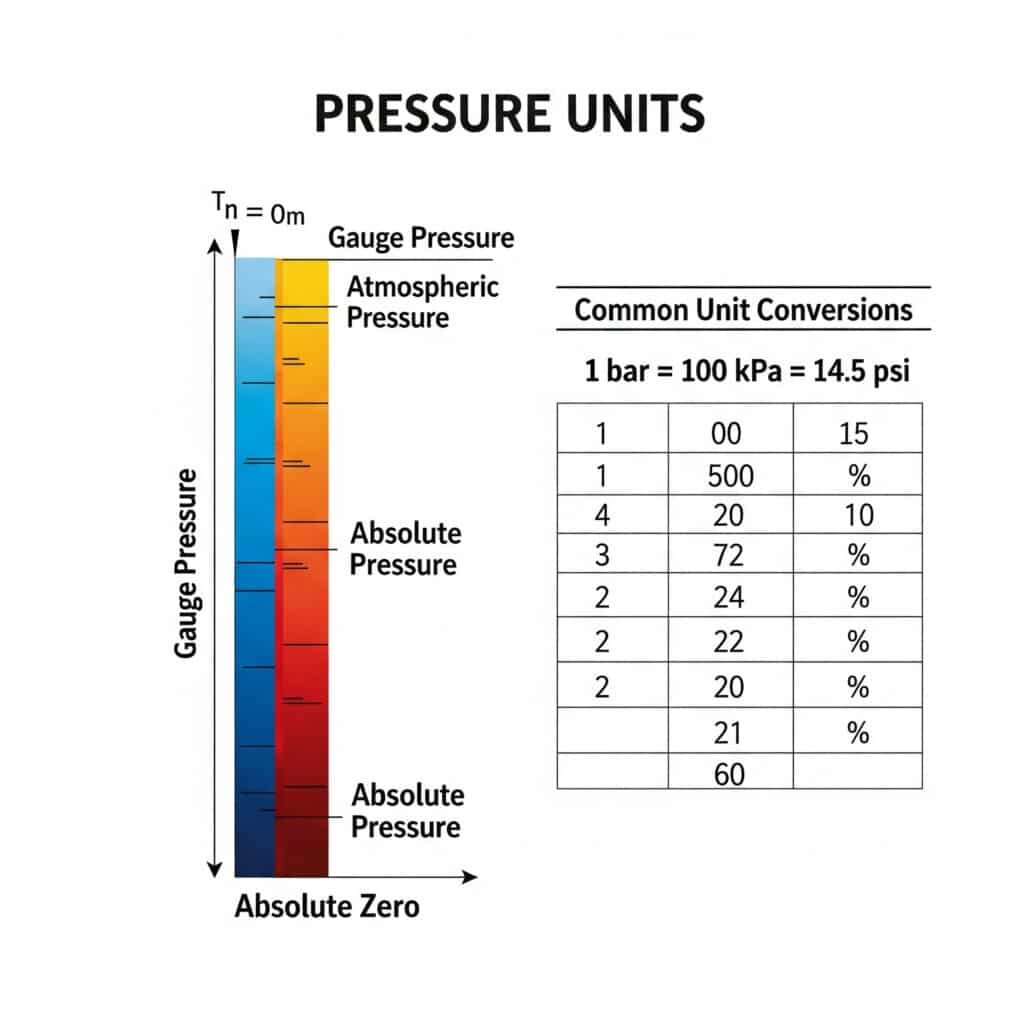
Veiledning for konvertering av enheter for absolutt trykk
Denne omfattende konverteringstabellen hjelper deg med å navigere i de ulike trykkenhetene som brukes over hele verden:
| Enhet | Symbol | Tilsvarende i Pa | Tilsvarende i bar | Ekvivalent i psi |
|---|---|---|---|---|
| Pascal | Pa | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| Bar | bar | 1 × 10⁵ | 1 | 14.5038 |
| Pund per kvadrattomme | psi | 6,894.76 | 0.0689476 | 1 |
| Kilogram kraft per kvadratcentimeter | kgf/cm² | 98,066.5 | 0.980665 | 14.2233 |
| Megapascal | MPa | 1 × 10⁶ | 10 | 145.038 |
| Atmosfære | atm | 101,325 | 1.01325 | 14.6959 |
| Torr | Torr | 133.322 | 0.00133322 | 0.0193368 |
| Millimeter kvikksølv | mmHg | 133.322 | 0.00133322 | 0.0193368 |
| Tommer vann | iH₂O | 249.089 | 0.00249089 | 0.0361274 |
Absolutt trykk vs. manometertrykk
Det er viktig å forstå forskjellen mellom absolutt trykk og manometertrykk:
Kalkulator for trykkomregning
Omregning av trykkenheter
Omformer for sylinderstrømningshastighet
Konverteringsformler
- P_absolutt = P_gauge + P_atmosfærisk
- P_gauge = P_absolutt - P_atmosfærisk
Hvor standard atmosfærisk trykk er omtrent:
- 1,01325 bar
- 14,7 psi
- 101 325 Pa
En gang jobbet jeg med et ingeniørteam i Tyskland som hadde kjøpt våre sylindere uten stang, men som rapporterte at de ikke oppnådde den forventede kraften. Etter litt feilsøking oppdaget vi at de brukte våre krafttabeller (som var basert på manometertrykk), men at de hadde lagt inn absolutte trykkverdier. Denne enkle misforståelsen førte til en feilberegning på 1 bar i kraftforventningene deres. Etter at vi hadde avklart trykkreferansen, fungerte systemet nøyaktig som spesifisert.
Praktiske eksempler på konvertering
La oss gå gjennom noen vanlige konverteringsscenarioer:
Eksempel 1: Konvertering av arbeidstrykk på tvers av enheter
En sylinder med et maksimalt arbeidstrykk på 0,7 MPa:
I baren:
0,7 MPa × 10 bar/MPa = 7 bar
I psi:
0,7 MPa × 145,038 psi/MPa = 101,5 psi
Eksempel 2: Konvertering fra manometer til absolutt trykk
Et system som opererer ved 6 bar overtrykk:
I absolutt trykk (bar):
6 bar_gauge + 1,01325 bar_atmosfærisk = 7,01325 bar_absolutt
Eksempel 3: Konvertering fra kgf/cm² til MPa
En japansk sylinder som er spesifisert for 7 kgf/cm²:
I MPa:
7 kgf/cm² × 0,0980665 MPa/(kgf/cm²) = 0,686 MPa
Regionale preferanser for trykkenheter
Ulike regioner bruker vanligvis forskjellige trykkenheter:
| Region | Vanlige trykkenheter |
|---|---|
| Nord-Amerika | psi, inHg, inH₂O |
| Europa | bar, Pa, mbar |
| Japan | kgf/cm², MPa |
| Kina | MPa, bar |
| STORBRITANNIA | bar, psi, Pa |
Trykkmåling i dokumentasjon
Når du dokumenterer trykkspesifikasjoner, er det viktig å angi dette tydelig:
- Den numeriske verdien
- Måleenheten
- Enten det er manometertrykk (g) eller absolutt trykk (a)
For eksempel:
- 6 bar_g (overtrykk, 6 bar over atmosfærisk trykk)
- 7,01 bar_a (absolutt trykk, totalt trykk inkludert atmosfærisk trykk)
Konklusjon
Å forstå fysikken bak pneumatiske sylindere - fra kraftberegninger i henhold til Pascals lov til strømnings- og trykkforhold og omregning av trykkenheter - er avgjørende for riktig systemdesign og feilsøking. Disse grunnleggende prinsippene bidrar til å sikre at de pneumatiske systemene dine leverer forventet ytelse på en pålitelig og effektiv måte.
Vanlige spørsmål om fysikk i pneumatiske systemer
Hvordan beregner jeg kraften til en stangløs pneumatisk sylinder?
For å beregne kraften fra en stangløs pneumatisk sylinder må du multiplisere driftstrykket med det effektive stempelarealet (F = P × A). For eksempel vil en sylinder uten stempelstang med 50 mm boring (0,001963 m² areal) som arbeider ved 6 bar (600 000 Pa), produsere en kraft på ca. 1178 N. I motsetning til tradisjonelle sylindere har sylindere uten stang vanligvis samme effektive areal i begge retninger.
Hvordan beregner jeg kraften til en stangløs pneumatisk sylinder?
For å beregne kraften fra en stangløs pneumatisk sylinder må du multiplisere driftstrykket med det effektive stempelarealet (F = P × A). For eksempel vil en sylinder uten stempelstang med 50 mm boring (0,001963 m² areal) som arbeider ved 6 bar (600 000 Pa), produsere en kraft på ca. 1178 N. I motsetning til tradisjonelle sylindere har sylindere uten stang vanligvis samme effektive areal i begge retninger.
Hva er forskjellen mellom overtrykk og absolutt trykk?
Manometertrykk (bar_g, psi_g) måler trykket i forhold til atmosfæretrykket, der atmosfæretrykket er null. Absolutt trykk (bar_a, psi_a) måler trykket i forhold til et perfekt vakuum, som er null. For å konvertere fra manometertrykk til absolutt trykk må du legge til atmosfæretrykket (ca. 1,01325 bar eller 14,7 psi) til måleravlesningen.
Hvordan påvirker luftstrømmen sylinderhastigheten?
Sylinderhastigheten er direkte proporsjonal med luftmengden og omvendt proporsjonal med stempelarealet (v = Q/A). Utilstrekkelig strømningshastighet på grunn av underdimensjonerte tilførselsledninger, restriktive koblinger eller utilstrekkelige ventiler vil begrense sylinderhastigheten uavhengig av trykket. For eksempel vil en strømningshastighet på 20 liter/sekund gjennom en sylinder med et stempelareal på 0,002 m² gi en hastighet på 10 meter/sekund.
Hvorfor beveger pneumatiske sylindere seg noen ganger langsommere enn beregnet?
Pneumatiske sylindere kan bevege seg langsommere enn beregnet på grunn av flere faktorer: begrensninger i lufttilførselen som forårsaker trykkfall, indre friksjon fra tetninger, mekaniske belastninger som overstiger beregningene, lekkasje som reduserer det effektive trykket, eller temperatureffekter på lufttettheten. I tillegg begrenser ventilens strømningskoeffisienter ofte den faktiske strømningshastigheten som er tilgjengelig for sylinderen.
Hvordan konverterer jeg mellom ulike trykkenheter for internasjonale spesifikasjoner?
For å konvertere mellom trykkenheter bruker du multiplikasjonsfaktorer: 1 bar = 100 000 Pa = 0,1 MPa = 14,5038 psi = 1,01972 kgf/cm². Kontroller alltid om trykket er angitt som manometer eller absolutt, da denne forskjellen kan påvirke beregningene betydelig. For eksempel tilsvarer 6 bar_g 7,01325 bar_a ved standard atmosfæriske forhold.
Hva er forholdet mellom sylinderboringens størrelse og kraftuttaket?
Forholdet mellom sylinderens boringsstørrelse og kraften som utløses, er kvadratisk - en dobling av boringsdiameteren øker kraften som utløses med fire ganger (siden areal = π × r²). Ved et driftstrykk på 6 bar produserer for eksempel en sylinder med 40 mm boring ca. 754 N kraft, mens en sylinder med 80 mm boring produserer ca. 3 016 N, nesten fire ganger så mye.
-
Gir en detaljert forklaring av Pascals lov, et grunnleggende prinsipp innen fluidmekanikk som er grunnlaget for hydraulisk og pneumatisk kraftoverføring. ↩
-
Gir en klar definisjon og sammenligning av overtrykk og absolutt trykk, noe som er avgjørende for nøyaktige tekniske beregninger, ettersom overtrykk er relativt til atmosfæretrykk. ↩
-
Forklarer utledning og anvendelse av Poiseuilles lov, som beskriver trykkfallet for en inkompressibel og newtonsk væske som strømmer gjennom et langt sylindrisk rør i laminært regime. ↩
-
Gir en teknisk definisjon av strømningskoeffisienten (Cv), et imperialt mål som gir en standardisert måte å sammenligne strømningskapasiteten til ulike ventiler på. ↩
-
Beskriver fysikken bak kvalt strømning, en fluiddynamisk tilstand som begrenser massestrømningshastigheten til en komprimerbar væske gjennom en restriksjon når hastigheten når lydens hastighet. ↩



