Jak rezonans wibracyjny wpływa na wydajność urządzeń przemysłowych?

Koszmarem każdego inżyniera utrzymania ruchu jest niespodziewana awaria sprzętu. Gdy maszyny wibrują z naturalną częstotliwością, w ciągu kilku minut może dojść do katastrofalnych uszkodzeń. Widziałem, jak ten problem kosztował firmy tysiące przestojów.

Rezonans wibracyjny¹ występuje, gdy siła zewnętrzna dopasowuje się do naturalnej częstotliwości systemu, powodując wzmocnione oscylacje, które mogą uszkodzić sprzęt. Zrozumienie i kontrolowanie tego zjawiska ma zasadnicze znaczenie dla zapobiegania awariom i wydłużania żywotności maszyn.

Podzielę się krótką historią. W zeszłym roku klient z Niemiec zadzwonił do mnie w panice. Ich linia produkcyjna została zatrzymana, ponieważ siłownik beztłoczyskowy wibrował gwałtownie. Problem? Rezonans. Pod koniec tego artykułu zrozumiesz, jak identyfikować i zapobiegać podobnym problemom w swoich systemach.

Spis treści

Formuła częstotliwości naturalnej: Jak obliczyć wrażliwe punkty systemu?
Model Mass-Spring: Dlaczego to uproszczone podejście jest tak cenne?
Optymalizacja współczynnika tłumienia: Jakie eksperymenty dają najlepsze wyniki?
Wnioski
Najczęściej zadawane pytania dotyczące rezonansu wibracyjnego

Formuła częstotliwości naturalnej: Jak obliczyć wrażliwe punkty systemu?

Zrozumienie częstotliwości drgań własnych sprzętu jest pierwszym krokiem w kierunku zapobiegania problemom związanym z rezonansem. Ta krytyczna wartość określa, kiedy system jest najbardziej podatny na problemy z wibracjami.

The częstotliwość drgań własnych² (fn) układu można obliczyć za pomocą wzoru: fn = (1/2π) × √(k/m), gdzie k to współczynnik sztywności, a m to masa. Obliczenia te ujawniają częstotliwość, przy której układ będzie rezonował, jeśli zostanie wzbudzony przez odpowiednie siły zewnętrzne.

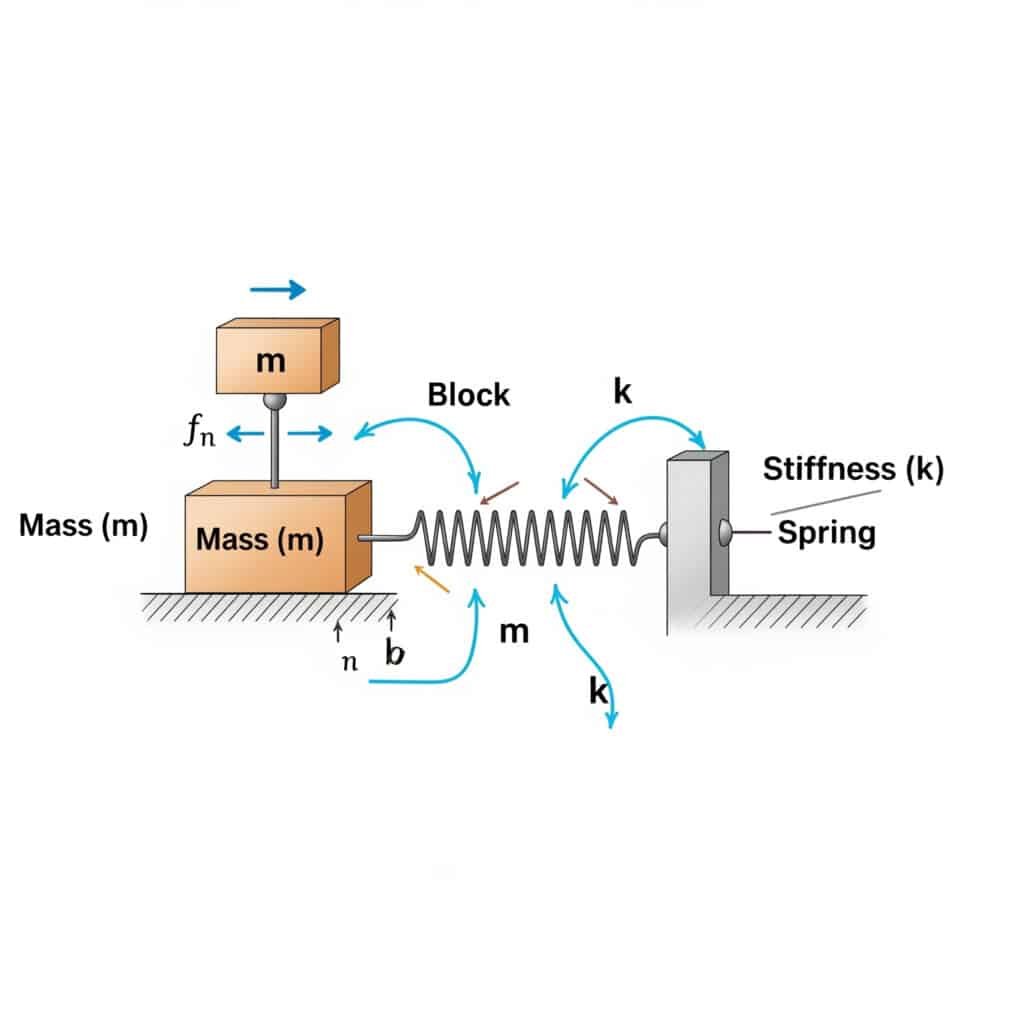
Czysty, edukacyjny diagram wyjaśniający częstotliwość drgań własnych. Ilustracja przedstawia prosty układ masa-sprężyna z blokiem oznaczonym jako "Masa (m)" i sprężyną oznaczoną jako "Sztywność (k)". Linie ruchu pokazują, że układ oscyluje. Obok wykresu wyraźnie widoczny jest wzór "fn = (1/2π) × √(k/m)", ze strzałkami wyraźnie łączącymi zmienne "m" i "k" w równaniu z odpowiednimi częściami fizycznymi. — częstotliwość drgań własnych

Kiedy odwiedziłem zakład produkcyjny w Szwajcarii, zauważyłem, że ich beztłoczyskowe siłowniki pneumatyczne ulegały przedwczesnym awariom. Ich zespół konserwacyjny nie obliczył częstotliwości drgań własnych układu. Po zastosowaniu tego wzoru stwierdziliśmy, że ich prędkość robocza była niebezpiecznie zbliżona do częstotliwości drgań własnych systemu.

Praktyczne zastosowania obliczeń częstotliwości drgań własnych

Wzór na częstotliwość drgań własnych nie jest tylko teoretyczny - ma on bezpośrednie zastosowanie w różnych warunkach przemysłowych:

Wybór sprzętu: Wybór komponentów o częstotliwościach naturalnych dalekich od warunków roboczych
Konserwacja zapobiegawcza: Planowanie inspekcji w oparciu o profile ryzyka drgań
Rozwiązywanie problemów: Identyfikacja pierwotnej przyczyny nieoczekiwanych wibracji

Typowe wartości częstotliwości drgań własnych dla komponentów przemysłowych

Komponent	Typowy zakres częstotliwości drgań własnych (Hz)
Siłowniki beztłoczyskowe	10-50 Hz
Wsporniki montażowe	20-100 Hz
Struktury wsparcia	5-30 Hz
Zawory sterujące	40-200 Hz

Czynniki krytyczne wpływające na częstotliwość drgań własnych

Obliczenie częstotliwości drgań własnych wydaje się proste, ale kilka czynników może komplikować rzeczywiste zastosowania:

Niejednorodny rozkład masy: Większość komponentów przemysłowych nie ma idealnie rozłożonej masy
Zmienna sztywność: Komponenty mogą mieć różną sztywność w różnych kierunkach.
Punkty połączeń: Sposób montażu komponentów znacząco wpływa na ich charakterystykę wibracji
Wpływ temperatury: Zarówno masa, jak i sztywność mogą zmieniać się wraz z temperaturą.

Model Mass-Spring: Dlaczego to uproszczone podejście jest tak cenne?

Model masa-sprężyna zapewnia intuicyjne ramy dla zrozumienia złożonych systemów wibracyjnych. Redukuje skomplikowane maszyny do podstawowych elementów, które inżynierowie mogą łatwo analizować.

The model masa-sprężyna³ upraszcza analizę drgań, reprezentując systemy mechaniczne jako dyskretne masy połączone sprężynami. Takie podejście pozwala inżynierom przewidywać zachowanie systemu, identyfikować potencjalne problemy związane z rezonansem i opracowywać skuteczne rozwiązania bez skomplikowanej matematyki.

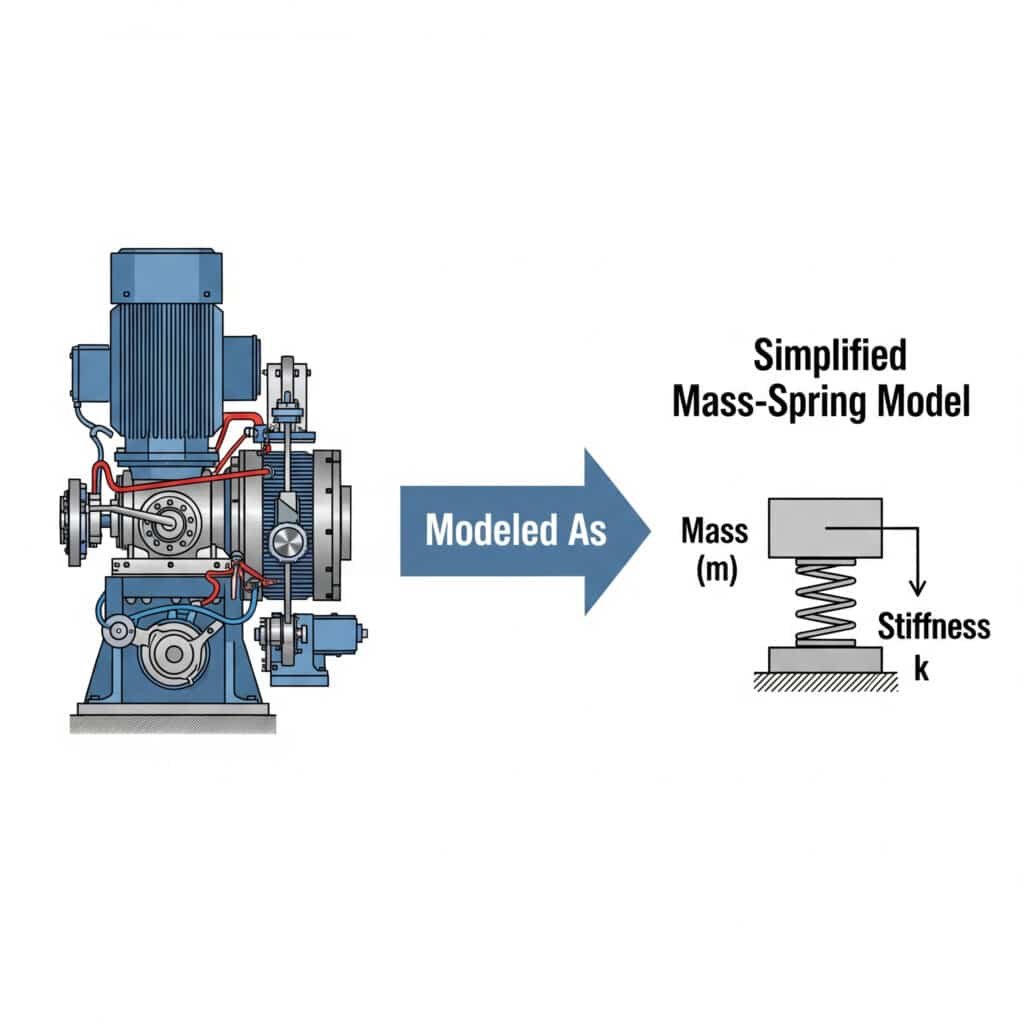
Infografika porównawcza wyjaśniająca model masa-sprężyna. Po lewej stronie, pod etykietą "Complex Mechanical System", znajduje się szczegółowa ilustracja silnika przemysłowego. Duża strzałka oznaczona jako "Modelowany jako" wskazuje w prawo. Po prawej stronie, pod etykietą "Uproszczony model masowo-sprężynowy", cały złożony silnik jest reprezentowany przez prosty blok oznaczony jako "Masa (m)" połączony z prostą sprężyną oznaczoną jako "Sztywność (k)". — model masa-sprężyna

Pamiętam, jak pracowałem z producentem części samochodowych w Michigan, który nie mógł zrozumieć, dlaczego jego cylindry beztłoczyskowe ulegały awariom. Modelując ich system jako prosty układ masa-sprężyna, zidentyfikowaliśmy, że wsporniki montażowe działały jak niezamierzone sprężyny, tworząc stan rezonansu.

Konwersja systemów rzeczywistych na modele masowo-sprężyste

Aby zastosować to podejście do swojego sprzętu:

Identyfikacja kluczowych mas: Określenie, które komponenty mają znaczący wpływ na wagę
Lokalizacja elementów sprężynowych: Znajdź komponenty, które magazynują i uwalniają energię (rzeczywiste sprężyny, elastyczne mocowania itp.).
Połączenia na mapie: Dokumentacja interakcji mas i sprężyn
Uproszczenie: Łączenie podobnych elementów w celu stworzenia łatwego w zarządzaniu modelu.

Rodzaje systemów sprężyn masowych

Typ systemu	Opis	Typowe zastosowania
Pojedynczy DOF	Jedna masa z jedną sprężyną	Proste siłowniki pneumatyczne
Multi-DOF	Wiele mas z wieloma sprężynami	Złożone maszyny z wieloma komponentami
Ciągły	Nieskończony DOF (wymaga innej analizy)	Belki, płyty i powłoki

Rozważania dotyczące zaawansowanego modelowania

Podczas gdy podstawowy model masowo-sprężynowy jest wartościowy, kilka ulepszeń czyni go bardziej realistycznym:

Dodawanie amortyzatorów: Rzeczywiste systemy zawsze rozpraszają energię
Uwzględnienie nieliniowości: Sprężyny nie zawsze podążają za Prawo Hooke'a⁴ doskonale
Rozliczanie wymuszonych wibracji: Siły zewnętrzne zmieniają zachowanie systemu
Uwzględnienie efektów sprzężenia: Ruch w jednym kierunku może wpływać na inne kierunki

Optymalizacja współczynnika tłumienia: Jakie eksperymenty dają najlepsze wyniki?

Tłumienie jest najlepszą obroną przed problemami związanymi z rezonansem. Znalezienie optymalnego współczynnika tłumienia poprzez eksperymenty może znacznie poprawić wydajność i niezawodność systemu.

Współczynnik tłumienia⁵ Eksperymenty optymalizacyjne polegają na systematycznym testowaniu różnych konfiguracji tłumienia w celu znalezienia idealnej równowagi między kontrolą drgań a szybkością reakcji systemu. Optymalny współczynnik tłumienia zazwyczaj mieści się w przedziale od 0,2 do 0,7, zapewniając wystarczające tłumienie drgań bez nadmiernej utraty energii.

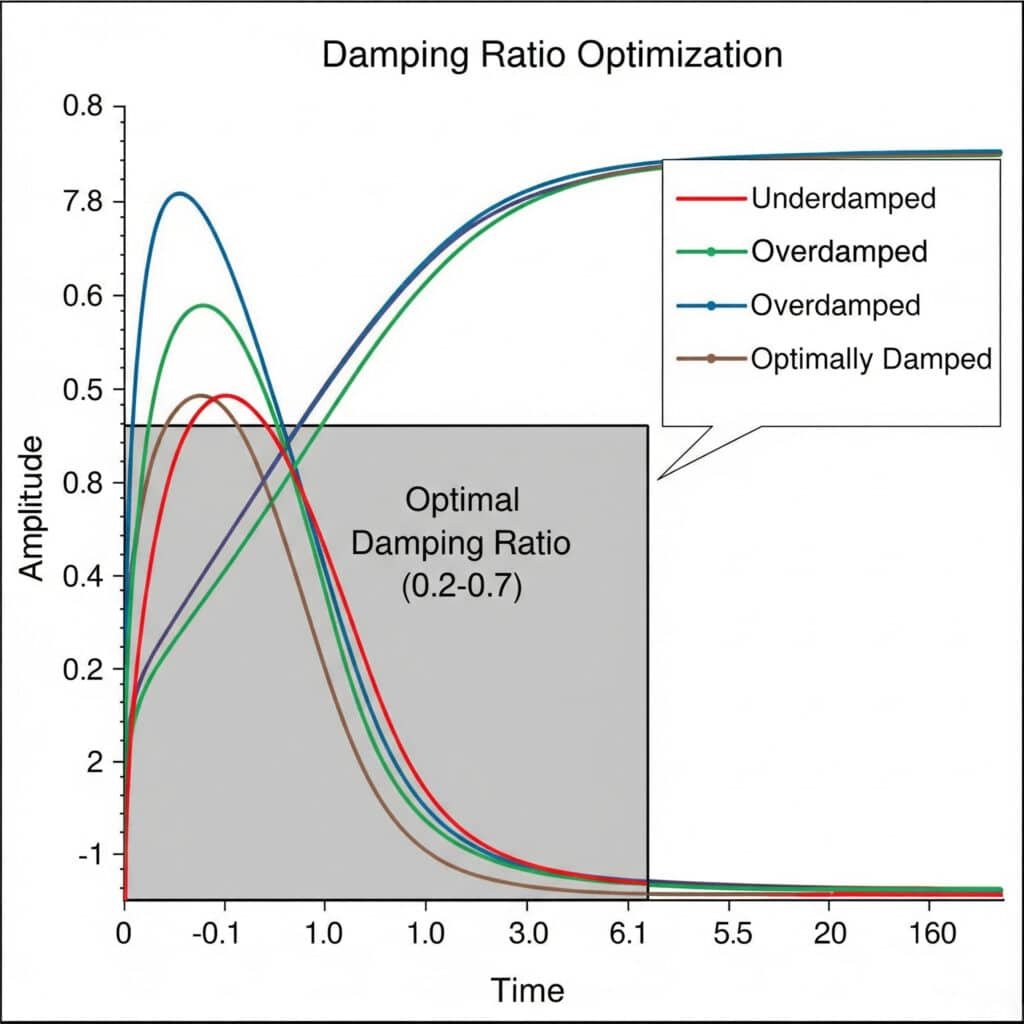
Wykres ilustrujący optymalizację współczynnika tłumienia poprzez wykreślenie "amplitudy" systemu w funkcji "czasu". Pokazuje on trzy różne krzywe odpowiedzi: krzywą "Underdamped", która znacznie oscyluje, krzywą "Overdamped", która bardzo powoli powraca do zera bez oscylacji, oraz krzywą "Optimally Damped", która szybko osiada z minimalnym przeregulowaniem. Zacieniony obszar podkreśla tę idealną odpowiedź, oznaczoną jako "Optimal Damping Ratio (0.2-0.7)". — optymalizacja współczynnika tłumienia

W zeszłym miesiącu pomogłem producentowi sprzętu do przetwórstwa spożywczego we Francji rozwiązać uporczywe problemy z wibracjami w ich magnetycznych cylindrach beztłoczyskowych. Dzięki serii eksperymentów ze współczynnikiem tłumienia odkryliśmy, że ich oryginalna konstrukcja miała współczynnik tłumienia wynoszący zaledwie 0,05 - o wiele za niski, aby zapobiec problemom z rezonansem.

Konfiguracja eksperymentalna do testowania współczynnika tłumienia

Przeprowadzenie skutecznych eksperymentów optymalizacji tłumienia:

Pomiar wyjściowy: Zapis odpowiedzi systemu bez dodatkowego tłumienia
Testowanie przyrostowe: Dodawanie elementów tłumiących w kontrolowanych przyrostach
Pomiar odpowiedzi: Pomiar amplitudy, czasu ustalania i charakterystyki częstotliwościowej.
Analiza danych: Oblicz współczynnik tłumienia dla każdej konfiguracji
Walidacja: Weryfikacja wydajności w rzeczywistych warunkach pracy

Porównanie technologii tłumienia

Technologia tłumienia	Zalety	Ograniczenia	Typowe zastosowania
Tłumiki wiskotyczne	Przewidywalna wydajność, stabilna temperatura	Wymagają konserwacji, potencjalne wycieki	Maszyny ciężkie, sprzęt precyzyjny
Tłumiki tarcia	Prosta konstrukcja, opłacalność	Zużycie w czasie, nieliniowe zachowanie	Podpory strukturalne, maszyny podstawowe
Tłumienie materiału	Brak ruchomych części, kompaktowe wymiary	Ograniczony zakres regulacji	Przyrządy precyzyjne, izolacja drgań
Aktywne tłumienie	Możliwość dostosowania do zmieniających się warunków	Złożony, wymaga zasilania	Zastosowania krytyczne, urządzenia o zmiennej prędkości

Optymalizacja tłumienia dla różnych warunków pracy

Idealny współczynnik tłumienia nie jest uniwersalny - zależy on od konkretnego zastosowania:

Szybkie operacje: Niższe współczynniki tłumienia (0,1-0,3) utrzymują szybkość reakcji.
Aplikacje precyzyjne: Wyższe współczynniki tłumienia (0,5-0,7) zapewniają stabilność
Systemy o zmiennym obciążeniu: Tłumienie adaptacyjne może być konieczne
Środowiska wrażliwe na temperaturę: Rozważ materiały tłumiące o stabilnych właściwościach

Studium przypadku: Optymalizacja tłumienia cylindrów beztłoczyskowych

Optymalizując siłownik beztłoczyskowy dwustronnego działania dla maszyny pakującej, przetestowaliśmy pięć różnych konfiguracji tłumienia:

Standardowe poduszki końcowe: Współczynnik tłumienia = 0,12
Wydłużone poduszki: Współczynnik tłumienia = 0,25
Zewnętrzne amortyzatory: Współczynnik tłumienia = 0,41
Kompozytowe wsporniki montażowe: Współczynnik tłumienia = 0,38
Podejście łączone (3+4): Współczynnik tłumienia = 0,53

Połączone podejście zapewniło najlepszą wydajność, zmniejszając amplitudę drgań o 78% przy zachowaniu akceptowalnego czasu reakcji.

Wnioski

Zrozumienie rezonansu drgań poprzez obliczenia częstotliwości drgań własnych, modelowanie masy i sprężyny oraz optymalizację współczynnika tłumienia ma kluczowe znaczenie dla zapobiegania awariom sprzętu. Stosując te zasady, można wydłużyć żywotność maszyn, skrócić czas przestojów i poprawić ogólną wydajność systemu.

Najczęściej zadawane pytania dotyczące rezonansu wibracyjnego

Czym jest rezonans wibracyjny w urządzeniach przemysłowych?

Rezonans wibracyjny występuje, gdy siła zewnętrzna dopasowuje się do naturalnej częstotliwości systemu, powodując wzmocnione oscylacje. W urządzeniach przemysłowych zjawisko to może prowadzić do nadmiernego ruchu, zmęczenia komponentów i katastrofalnych awarii, jeśli nie jest odpowiednio zarządzane.

Jak mogę zidentyfikować, czy mój system doświadcza rezonansu?

Poszukaj objawów, takich jak niewyjaśniony wzrost hałasu, widoczne wibracje przy określonych prędkościach, przedwczesne awarie komponentów i pogorszenie wydajności, które występuje w stałych punktach pracy. Narzędzia do analizy drgań mogą potwierdzić warunki rezonansu.

Jaka jest różnica między wymuszonymi wibracjami a rezonansem?

Wibracje wymuszone występują zawsze, gdy na układ działa siła zewnętrzna, podczas gdy rezonans jest specyficznym stanem, w którym częstotliwość wymuszająca pokrywa się z częstotliwością drgań własnych układu, co skutkuje wzmocnioną reakcją. Każdy rezonans wiąże się z wymuszonymi wibracjami, ale nie wszystkie wymuszone wibracje powodują rezonans.

W jaki sposób konstrukcja beztłoczyskowego siłownika pneumatycznego wpływa na jego charakterystykę drgań?

Konstrukcja beztłoczyskowych siłowników pneumatycznych - z ich ruchomym wózkiem, wewnętrznym systemem uszczelniającym i mechanizmami prowadzącymi - stwarza wyjątkowe wyzwania związane z wibracjami. Wydłużony profil działa jak belka, która może się zginać, masa wózka wytwarza siły bezwładności, a taśmy uszczelniające mogą wprowadzać zmienne tarcie.

Jakie proste modyfikacje mogą zmniejszyć rezonans w istniejącym sprzęcie?

W przypadku istniejącego sprzętu, w którym występują problemy z rezonansem, należy rozważyć dodanie masy w celu zmiany częstotliwości drgań własnych, zainstalowanie zewnętrznych tłumików lub amortyzatorów, zmodyfikowanie metod montażu w celu uwzględnienia izolacji drgań lub dostosowanie prędkości roboczych w celu uniknięcia częstotliwości rezonansowych.

Zapewnia podstawowe wyjaśnienie rezonansu mechanicznego, często z przykładami wizualnymi, pokazując, w jaki sposób niewielka okresowa siła może wytwarzać oscylacje o dużej amplitudzie w systemie. ↩
Oferuje szczegółowe spojrzenie na fizykę częstotliwości drgań własnych, określonej częstotliwości, przy której system ma tendencję do oscylacji przy braku jakiejkolwiek siły napędowej lub tłumiącej. ↩
Wyjaśnia zasady modelu masa-sprężyna, podstawowej idealizacji w fizyce i inżynierii wykorzystywanej do analizy złożonych systemów, które wykazują prosty ruch harmoniczny. ↩
Szczegóły Prawo Hooke'a, zasada fizyki, która mówi, że siła potrzebna do rozciągnięcia lub ściśnięcia sprężyny na pewną odległość jest wprost proporcjonalna do tej odległości. ↩
Opisuje współczynnik tłumienia, bezwymiarową miarę, która określa, w jaki sposób oscylacje w systemie zanikają po zakłóceniu, co ma kluczowe znaczenie dla kontrolowania rezonansu. ↩

Witam, jestem Chuck, starszy ekspert z 15-letnim doświadczeniem w branży pneumatycznej. W Bepto Pneumatic koncentruję się na dostarczaniu wysokiej jakości rozwiązań pneumatycznych dostosowanych do potrzeb naszych klientów. Moja wiedza obejmuje automatykę przemysłową, projektowanie i integrację systemów pneumatycznych, a także zastosowanie i optymalizację kluczowych komponentów. Jeśli masz jakieś pytania lub chciałbyś omówić swoje potrzeby projektowe, skontaktuj się ze mną pod adresem chuck@bepto.com.