
Czy zmagasz się z niespójnymi prędkościami siłowników pneumatycznych lub nieoczekiwanymi uderzeniami na końcu suwu? Te powszechne problemy często wynikają ze słabego zrozumienia kinematyki tłoka. Wielu inżynierów koncentruje się wyłącznie na wymaganiach dotyczących siły, pomijając krytyczne parametry ruchu, które decydują o wydajności systemu.
Kinematyka tłoka1 mają bezpośredni wpływ na wydajność systemu pneumatycznego poprzez zależności ciśnienie-prędkość, limity przyspieszeń i wymagania dotyczące amortyzacji. Zrozumienie tych zasad pozwala inżynierom odpowiednio dobrać komponenty, przewidzieć rzeczywiste profile ruchu i zapobiec przedwczesnym awariom siłowników beztłoczyskowych i innych siłowników pneumatycznych.
W ciągu ponad 15 lat pracy w Bepto nad systemami pneumatycznymi widziałem niezliczone przypadki, w których zrozumienie tych podstawowych zasad pomogło klientom rozwiązać uporczywe problemy z wydajnością i wydłużyć żywotność sprzętu o 3-5 razy.
Spis treści
- Jakiego ciśnienia potrzebujesz do poruszania się ze stałą prędkością?
- Jak obliczyć maksymalne możliwe przyspieszenie w siłownikach pneumatycznych?
- Dlaczego czas amortyzacji ma znaczenie i jak się go oblicza?
- Wnioski
- Najczęściej zadawane pytania dotyczące kinematyki tłoków w układach pneumatycznych
Jakiego ciśnienia potrzebujesz do poruszania się ze stałą prędkością?
Wielu inżynierów po prostu stosuje maksymalne dostępne ciśnienie w swoich układach pneumatycznych, ale takie podejście jest nieefektywne i może prowadzić do gwałtownych ruchów, nadmiernego zużycia i marnowania energii.
Ciśnienie wymagane do ruchu ze stałą prędkością w siłowniku pneumatycznym jest obliczane przy użyciu wzoru P = (F + Fr)/A, gdzie P to ciśnienie, F to siła obciążenia zewnętrznego, Fr to opór tarcia, a A to powierzchnia tłoka. Obliczenie to zapewnia płynną, wydajną pracę bez nadmiernego ciśnienia, które marnuje energię i przyspiesza zużycie podzespołów.
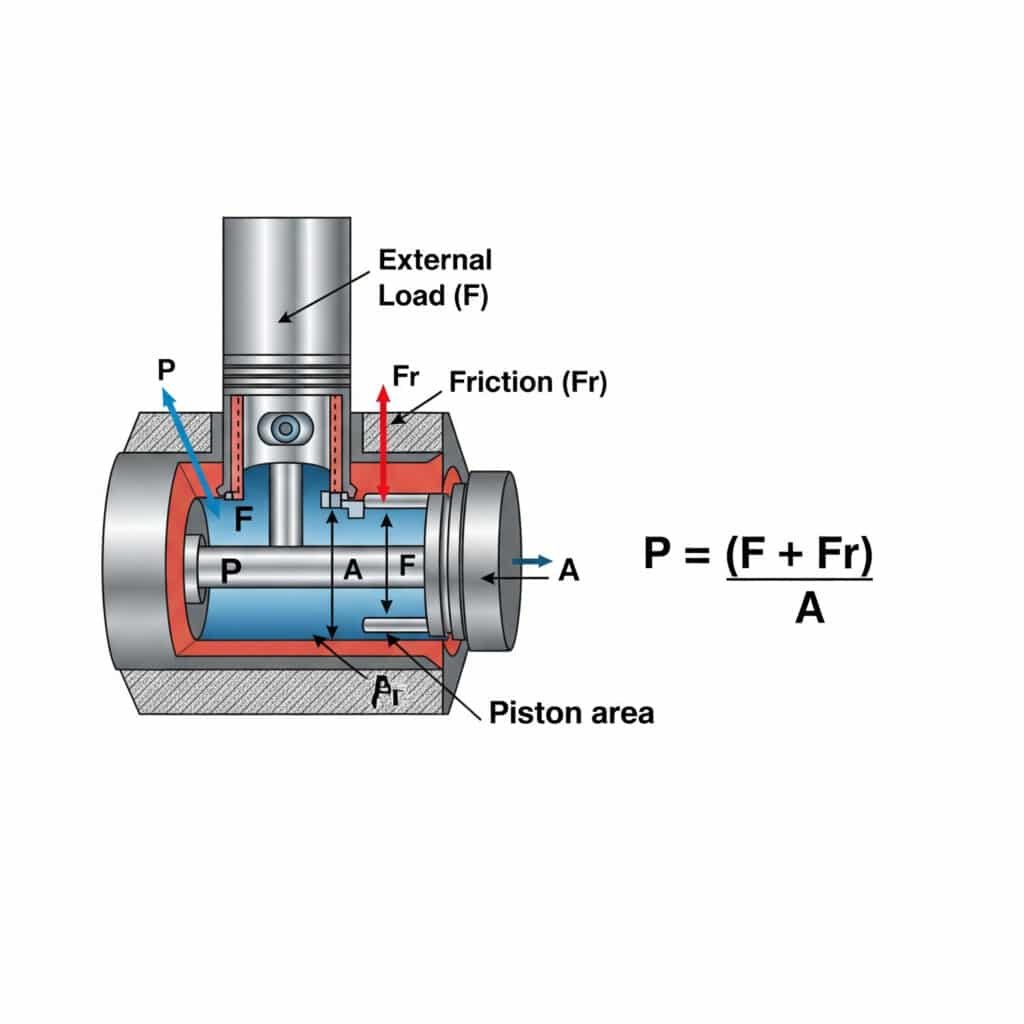
Zrozumienie wymagań ciśnieniowych dla ruchu ze stałą prędkością ma praktyczne implikacje dla projektowania i działania systemu. Pozwól, że podzielę to na praktyczne spostrzeżenia.
Czynniki wpływające na wymagania dotyczące ciśnienia dla stałej prędkości
Ciśnienie potrzebne do utrzymania stałej prędkości zależy od kilku czynników:
| Czynnik | Wpływ na wymagania dotyczące ciśnienia | Rozważania praktyczne |
|---|---|---|
| Obciążenie zewnętrzne | Bezpośrednia zależność liniowa | Zmienia się w zależności od orientacji i sił zewnętrznych |
| Tarcie | Zwiększa wymagane ciśnienie | Zmiany związane ze zużyciem uszczelnienia i smarowaniem |
| Obszar tłoka | Odwrotnie proporcjonalne | Większy otwór = niższe zapotrzebowanie na ciśnienie |
| Ograniczenia w dostawie powietrza | Spadki ciśnienia w przewodach/zaworach | Komponenty dobrane pod kątem minimalnego spadku ciśnienia |
| Ciśnienie wsteczne | Sprzeciwia się wnioskowi | Wydajność przepływu spalin |
Obliczanie minimalnego ciśnienia dla stabilnego ruchu
Określenie minimalnego ciśnienia potrzebnego do stabilnego ruchu:
- Oblicz siłę wymaganą do pokonania obciążenia zewnętrznego
- Dodaj siłę tarcia (zazwyczaj 3-20% maksymalnej siły).
- Podziel przez efektywną powierzchnię tłoka
- Dodaj współczynnik stabilności (zazwyczaj 10-30%)
Na przykład w cylindrze beztłoczyskowym o średnicy 40 mm z obciążeniem 10 kg i tarciem 15%:
| Parametr | Kalkulacja | Wynik |
|---|---|---|
| Siła obciążenia | 10 kg × 9,81 m/s² | 98.1N |
| Siła tarcia | 15% maksymalnej siły przy 6 barach | ~45N |
| Całkowita siła | 98.1N + 45N | 143.1N |
| Obszar tłoka | π × (0,02m)² | 0.00126m² |
| Minimalne ciśnienie | 143.1N ÷ 0.00126m² | 113 571 Pa (1,14 bar) |
| Ze współczynnikiem stabilności 20% | 1,14 bar × 1,2 | 1,37 bara |
Zastosowanie w świecie rzeczywistym: Oszczędność energii dzięki optymalizacji ciśnienia
W zeszłym roku pracowałem z Robertem, inżynierem produkcji w zakładzie produkującym meble w Michigan. Jego zautomatyzowana linia montażowa wykorzystywała siłowniki beztłoczyskowe działające przy pełnym ciśnieniu zasilania 6 barów, niezależnie od obciążenia.
Po przeanalizowaniu jego aplikacji ustaliliśmy, że większość ruchów wymaga jedynie 2,5-3 barów do stabilnej pracy. Instalując Proporcjonalne regulatory ciśnieniaZmniejszyliśmy zużycie powietrza o 40% przy zachowaniu tego samego czasu cyklu. Pozwoliło to zaoszczędzić około $12,000 rocznie na kosztach energii, jednocześnie zmniejszając zużycie uszczelnienia i wydłużając okresy między konserwacjami.
Zależność prędkość-ciśnienie w układach rzeczywistych
W praktyce zależność między ciśnieniem a prędkością nie jest idealnie liniowa ze względu na:
- Ograniczenia przepływu: Rozmiar zaworu i portu wpływa na maksymalną osiągalną prędkość
- Efekty ściśliwości: Powietrze jest ściśliwe, co powoduje opóźnienia przyspieszenia.
- Zjawisko poślizgu: Charakterystyka tarcia zmienia się wraz z prędkością
- Efekty bezwładnościowe: Przyspieszenie masy wymaga dodatkowej siły/ciśnienia
Jak obliczyć maksymalne możliwe przyspieszenie w siłownikach pneumatycznych?
Zrozumienie limitów przyspieszenia ma kluczowe znaczenie dla zapobiegania nadmiernym wstrząsom, wibracjom i przedwczesnym awariom komponentów w systemach pneumatycznych.
Maksymalne możliwe przyspieszenie w siłowniku pneumatycznym jest obliczane przy użyciu wzoru a = (P × A - F - Fr)/m, gdzie a to przyspieszenie, P to ciśnienie, A to powierzchnia tłoka, F to obciążenie zewnętrzne, Fr to opór tarcia, a m to poruszająca się masa. Równanie to określa fizyczne granice szybkości, z jaką siłownik pneumatyczny może rozpocząć lub zatrzymać ruch.
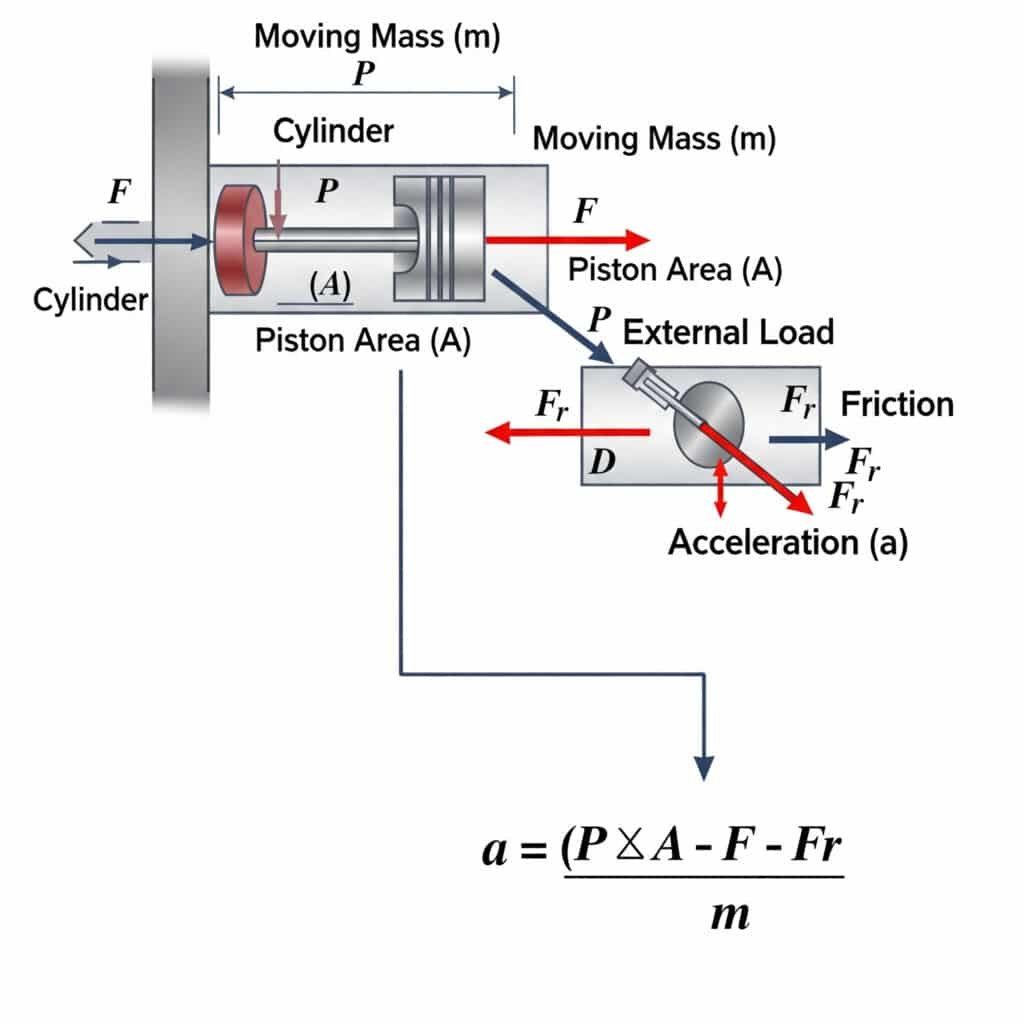
Teoretyczne limity przyspieszenia mają znaczące praktyczne implikacje dla projektowania systemu i wyboru komponentów.
Wyprowadzenie równania granicznego przyspieszenia
Równanie limitu przyspieszenia pochodzi z Drugie prawo Newtona2 (F = ma):
- Siła netto dostępna dla przyspieszenia wynosi: Fnet = Fpressure - Fload - Ffriction
- Ciśnienie F = P × A
- Zatem: a = Fnet/m = (P × A - F - Fr)/m
Praktyczne limity przyspieszenia dla różnych typów cylindrów
Różne konstrukcje cylindrów mają różne praktyczne limity przyspieszenia:
| Typ cylindra | Typowe maksymalne przyspieszenie | Czynniki ograniczające |
|---|---|---|
| Standardowy siłownik prętowy | 10-15 m/s² | Wyboczenie pręta, obciążenia łożysk |
| Cylinder beztłoczyskowy (magnetyczny) | 8-12 m/s² | Siła sprzężenia magnetycznego |
| Cylinder beztłoczyskowy (mechaniczny) | 15-25 m/s² | Konstrukcja uszczelnienia/łożyska, tarcie wewnętrzne |
| Cylinder prowadzący | 20-30 m/s² | Sztywność systemu prowadnic, nośność |
| Cylinder udarowy | 50-100+ m/s² | Specjalnie zaprojektowany do dużych przyspieszeń |
Uwzględnienie masy w obliczeniach przyspieszenia
Przy obliczaniu przyspieszenia bardzo ważne jest uwzględnienie wszystkich poruszających się mas:
- Zespół tłoka: Zawiera tłok, uszczelki i elementy łączące.
- Masa ładunku: Przemieszczane obciążenie zewnętrzne
- Efektywna masa poruszającego się powietrza: Często nieistotne, ale istotne w zastosowaniach wymagających dużej prędkości.
- Dodatkowa masa wynikająca z elementów montażowych: Wsporniki, czujniki itp.
Pomogłem kiedyś klientowi we Francji, który doświadczał tajemniczych awarii w swoim systemie cylindrów beztłoczyskowych. Cylinder był prawidłowo dobrany do podanego obciążenia 15 kg, ale konsekwentnie ulegał awarii po kilku tysiącach cykli.
Po zbadaniu sprawy odkryliśmy, że nie uwzględnił on masy płyty montażowej i osprzętu wynoszącej 12 kg. Rzeczywista masa ruchoma była prawie dwukrotnie większa niż obliczona, powodując siły przyspieszenia przekraczające limity projektowe cylindra. Po wymianie siłownika na większy, awarie ustały całkowicie.
Metody kontroli przyspieszenia
Kontrola przyspieszenia w bezpiecznych granicach:
- Zawory sterujące przepływem: Ograniczenie natężenia przepływu podczas ruchu początkowego
- Zawory proporcjonalne: Zapewnienie kontrolowanego wzrostu ciśnienia
- Przyspieszenie wielostopniowe: Użyj stopniowego wzrostu ciśnienia
- Tłumienie mechaniczne: Dodaj zewnętrzne amortyzatory
- Sterowanie elektroniczne: Użycie systemy serwo-pneumatyczne3 ze sprzężeniem zwrotnym przyspieszenia
Dlaczego czas amortyzacji ma znaczenie i jak się go oblicza?
Prawidłowa amortyzacja na końcu suwu ma zasadnicze znaczenie dla zapobiegania uszkodzeniom udarowym, redukcji hałasu i wydłużenia żywotności siłowników pneumatycznych. Zrozumienie czasu amortyzacji pomaga inżynierom projektować systemy, które równoważą czas cyklu z długowiecznością komponentów.
Czas amortyzacji w siłownikach pneumatycznych jest obliczany za pomocą równania t = √(2s/a), gdzie t to czas, s to długość skoku amortyzacji, a a to opóźnienie. Czas ten określa, ile czasu potrzeba, aby bezpiecznie wyhamować poruszającą się masę przed uderzeniem, co ma kluczowe znaczenie dla zapobiegania uszkodzeniom siłownika i dołączonych do niego komponentów.

Przyjrzyjmy się praktycznym aspektom obliczeń czasu amortyzacji i ich implikacjom dla projektowania systemu.
Fizyka stojąca za amortyzacją pneumatyczną
Amortyzacja pneumatyczna działa poprzez kontrolowane sprężanie powietrza i ograniczony wydech:
- Gdy tłok wchodzi do komory poduszki, droga wydechu jest ograniczona
- Uwięzione powietrze spręża się, tworząc rosnące przeciwciśnienie
- To przeciwciśnienie wytwarza przeciwną siłę, która spowalnia tłok
- Profil opóźnienia zależy od konstrukcji i regulacji poduszki
Obliczanie optymalnego czasu amortyzacji
Optymalny czas amortyzacji równoważy zapobieganie uderzeniom z wydajnością cyklu:
| Parametr | Formuła | Przykład |
|---|---|---|
| Odległość amortyzacji | W oparciu o konstrukcję cylindra | 15 mm (typowo dla otworu 40 mm) |
| Wymagane opóźnienie | a = v²/(2s) | Dla v=0.5m/s, s=15mm: a = 8.33m/s² |
| Czas amortyzacji | t = √(2s/a) | t = √(2×0.015/8.33) = 0.06s |
| Wzrost ciśnienia | P = P₀(V₀/V)^γ | Zależy od geometrii komory poduszki |
Czynniki wpływające na wydajność amortyzacji
Na rzeczywistą wydajność amortyzacji wpływa kilka czynników:
- Konstrukcja uszczelnienia poduszkowego: Wpływa na wyciek powietrza podczas amortyzacji
- Regulacja zaworu iglicowego: Kontroluje stopień ograniczenia wydechu
- Poruszająca się masa: Cięższe ładunki wymagają dłuższego czasu amortyzacji
- Prędkość zbliżania się: Wyższe prędkości wymagają większej odległości między poduszkami
- Ciśnienie robocze: Wpływa na maksymalną dostępną przeciwsiłę
Rodzaje amortyzacji i ich zastosowania
Różne mechanizmy amortyzacji są odpowiednie do różnych zastosowań:
| Typ amortyzacji | Charakterystyka | Najlepsze aplikacje |
|---|---|---|
| Stała amortyzacja | Prosty, bez możliwości regulacji | Niewielkie obciążenia, stabilna praca |
| Regulowana amortyzacja | Możliwość dostrajania za pomocą zaworów iglicowych | Zmienne obciążenia, elastyczne zastosowania |
| Samoregulująca się amortyzacja | Dostosowuje się do różnych warunków | Zmiana prędkości i obciążenia |
| Zewnętrzne amortyzatory | Wysoka absorpcja energii | Duże obciążenia, wysokie prędkości |
| Elektroniczna amortyzacja | Precyzyjnie kontrolowane zwalnianie | Systemy serwo-pneumatyczne |
Studium przypadku: Optymalizacja amortyzacji w aplikacjach o wysokim cyklu pracy
Niedawno współpracowałem z Thomasem, inżynierem projektantem w firmie produkującej części samochodowe w Niemczech. Jego linia montażowa wykorzystywała siłowniki beztłoczyskowe pracujące z prędkością 45 cykli na minutę, ale często dochodziło do awarii uszczelnień i uszkodzeń wsporników montażowych.
Analiza wykazała, że czas amortyzacji był zbyt krótki dla poruszającej się masy, powodując siły uderzenia prawie 3G na każdym końcu skoku. Zwiększając skok amortyzacji z 12 mm do 20 mm i optymalizując ustawienia zaworu iglicowego, wydłużyliśmy czas amortyzacji z 0,04 s do 0,07 s.
Ta pozornie niewielka zmiana zmniejszyła siłę uderzenia o ponad 60%, całkowicie wyeliminowała uszkodzenia wspornika i wydłużyła żywotność uszczelnienia z 3 miesięcy do ponad roku - a wszystko to przy zachowaniu wymaganego czasu cyklu.
Praktyczna procedura regulacji amortyzacji
Zapewnia optymalną amortyzację w siłownikach beztłoczyskowych:
- Rozpocznij z całkowicie otwartymi zaworami poduszki (minimalne ograniczenie).
- Stopniowo zamykać zawór poduszki powietrznej, aż do uzyskania płynnego zwalniania.
- Test przy minimalnym i maksymalnym oczekiwanym obciążeniu
- Weryfikacja wydajności amortyzacji w pełnym zakresie prędkości
- Słuchaj dźwięków uderzenia, które wskazują na niewystarczającą amortyzację.
- Zmierz rzeczywisty czas zwalniania, aby potwierdzić obliczenia
Wnioski
Zrozumienie zasad kinematyki tłoka - od wymagań ciśnieniowych dla stałej prędkości do limitów przyspieszenia i obliczeń czasu amortyzacji - jest niezbędne do projektowania wydajnych, niezawodnych systemów pneumatycznych. Stosując te zasady w aplikacjach z siłownikami beztłoczyskowymi, można zoptymalizować wydajność, zmniejszyć zużycie energii i znacznie wydłużyć żywotność komponentów.
Najczęściej zadawane pytania dotyczące kinematyki tłoków w układach pneumatycznych
Jakiego ciśnienia potrzebuję dla określonej prędkości cylindra?
Wymagane ciśnienie zależy od obciążenia, tarcia i powierzchni cylindra. Oblicz je za pomocą wzoru P = (F + Fr)/A, gdzie F to zewnętrzna siła obciążenia, Fr to opór tarcia, a A to powierzchnia tłoka. W przypadku typowego cylindra beztłoczyskowego poruszającego ładunek o masie 10 kg w poziomie, do stabilnego ruchu przy umiarkowanych prędkościach potrzeba około 1,5-2 barów.
Jak szybko może przyspieszyć siłownik pneumatyczny?
Maksymalne przyspieszenie siłownika pneumatycznego jest obliczane przy użyciu wzoru a = (P × A - F - Fr)/m. Typowe siłowniki beztłoczyskowe mogą osiągnąć przyspieszenie 10-25 m/s² w zależności od konstrukcji. Przekłada się to na osiągnięcie prędkości 0,5 m/s w około 20-50 milisekund w optymalnych warunkach.
Jakie czynniki ograniczają maksymalną prędkość cylindra beztłoczyskowego?
Maksymalna prędkość jest ograniczona wydajnością przepływu zaworu, objętością dostarczanego powietrza, wielkością portu, możliwościami amortyzacji i konstrukcją uszczelnienia. Większość standardowych siłowników beztłoczyskowych jest zaprojektowana dla maksymalnych prędkości 0,8-1,5 m/s, choć wyspecjalizowane szybkie konstrukcje mogą osiągać 2-3 m/s.
Jak obliczyć odpowiednią amortyzację dla mojego zastosowania?
Oblicz odpowiednią amortyzację, określając energię kinetyczną (KE = ½mv²) poruszającego się ładunku i upewniając się, że system amortyzacji może pochłonąć tę energię. Czas amortyzacji należy obliczyć przy użyciu t = √(2s/a), gdzie s to odległość amortyzacji, a a to pożądana szybkość zwalniania.
Co się stanie, jeśli mój siłownik pneumatyczny przyspieszy zbyt szybko?
Nadmierne przyspieszenie może powodować naprężenia mechaniczne elementów montażowych, przedwczesne zużycie uszczelnień, zwiększone wibracje i hałas, potencjalne przesunięcie lub uszkodzenie obciążenia oraz zmniejszoną precyzję systemu. Może to również prowadzić do gwałtownych ruchów, które wpływają na jakość produktu w zastosowaniach precyzyjnych.
W jaki sposób orientacja ładunku wpływa na nacisk wymagany do ruchu?
Orientacja ładunku znacząco wpływa na wymagania dotyczące ciśnienia. Obciążenia pionowe poruszające się wbrew grawitacji wymagają dodatkowego ciśnienia, aby pokonać siłę grawitacji (P = F/A + Fg/A + Fr/A). Obciążenia poziome wymagają jedynie pokonania tarcia i bezwładności. Obciążenia nachylone mieszczą się pomiędzy tymi skrajnościami w oparciu o sinus kąta.
-
Zapewnia podstawowe wyjaśnienie kinematyki, gałęzi mechaniki, która opisuje ruch obiektów bez uwzględniania sił powodujących ruch.
elektroniczny sygnał wejściowy, umożliwiający zaawansowane sterowanie pneumatyczne. ↩ -
Szczegóły Drugie prawo Newtona (F=ma), fundamentalna zasada fizyki, która wiąże siłę działającą na obiekt z jego masą i przyspieszeniem, co stanowi podstawę wszystkich obliczeń dynamicznych. ↩
-
Opisuje serwopneumatykę, zaawansowaną technologię sterowania, która łączy moc pneumatyki z precyzją elektronicznego sterowania w zamkniętej pętli w celu uzyskania bardzo dokładnych profili pozycjonowania i ruchu. ↩


