
Czy kiedykolwiek dotknąłeś siłownik pneumatyczny po ciągłej pracy i był zaskoczony tym, jak bardzo jest gorący? Ciepło to nie tylko niedogodność - oznacza ono zmarnowaną energię, zmniejszoną wydajność i potencjalne problemy z niezawodnością, które mogą kosztować tysiące złotych.
Przenoszenie ciepła w układach pneumatycznych odbywa się poprzez trzy mechanizmy: przewodzenie przez materiały komponentów, konwekcję między powierzchniami i powietrzem oraz promieniowanie z gorących powierzchni. Zrozumienie i optymalizacja tych zasad może obniżyć temperaturę pracy o 15-30%, wydłużyć żywotność komponentów nawet o 40% i poprawić efektywność energetyczną o 5-15%.
W zeszłym miesiącu konsultowałem się z zakładem przetwórstwa spożywczego w Georgii, gdzie ich cylindry beztłoczyskowe ulegały awarii co 3-4 miesiące z powodu problemów termicznych. Ich zespół konserwacyjny po prostu wymieniał komponenty, nie zajmując się pierwotną przyczyną. Stosując odpowiednie zasady wymiany ciepła, obniżyliśmy temperaturę roboczą o 22°C i wydłużyliśmy żywotność komponentów do ponad roku. Pozwól, że pokażę Ci, jak to zrobiliśmy - i jak możesz zastosować te same zasady w swoich systemach.
Spis treści
- Obliczanie współczynnika przewodzenia: Jak ciepło przenika przez komponenty?
- Metody poprawy konwekcji: Jakie techniki maksymalizują wymianę ciepła powietrze-powierzchnia?
- Model efektywności promieniowania: Kiedy promieniowanie cieplne ma znaczenie w układach pneumatycznych?
- Wnioski
- Najczęściej zadawane pytania dotyczące wymiany ciepła w układach pneumatycznych
Obliczanie współczynnika przewodzenia: Jak ciepło przenika przez komponenty?
Przewodzenie jest głównym mechanizmem wymiany ciepła w stałych elementach pneumatycznych. Zrozumienie sposobu obliczania i optymalizacji współczynników przewodzenia jest niezbędne do zarządzania temperaturą systemu.
Współczynnik przewodzenia ciepła można obliczyć za pomocą wzoru Prawo Fouriera1q = -k(dT/dx), gdzie q to strumień ciepła (W/m²), k to przewodność cieplna (W/m-K), a dT/dx to gradient temperatury. W przypadku komponentów pneumatycznych efektywne przewodzenie zależy od wyboru materiału, jakości interfejsu i czynników geometrycznych, które wpływają na długość ścieżki ciepła i pole przekroju poprzecznego.
Pamiętam rozwiązywanie problemów na linii produkcyjnej w Tennessee, gdzie łożyska cylindrów beztłoczyskowych ulegały przedwczesnej awarii. Zespół konserwacyjny wypróbował wiele smarów bez powodzenia. Kiedy przeanalizowaliśmy ścieżki przewodzenia, odkryliśmy wąskie gardło termiczne na styku łożyska i obudowy. Poprawiając wykończenie powierzchni i stosując związek przewodzący ciepło, zwiększyliśmy efektywny współczynnik przewodzenia o 340% i całkowicie wyeliminowaliśmy awarie.
Podstawowe równania przewodzenia
Przeanalizujmy kluczowe równania do obliczania przewodzenia w komponentach pneumatycznych:
Prawo Fouriera dla przewodzenia ciepła
Podstawowe równanie regulujące przewodzenie ciepła to:
q = -k(dT/dx)
Gdzie:
- q = Strumień ciepła (W/m²)
- k = Przewodność cieplna (W/m-K)
- dT/dx = gradient temperatury (K/m)
Dla prostego przypadku jednowymiarowego o stałym przekroju:
Q = kA(T₁-T₂)/L
Gdzie:
- Q = Współczynnik przenikania ciepła (W)
- A = Pole przekroju poprzecznego (m²)
- T₁, T₂ = temperatury na każdym końcu (K)
- L = Długość ścieżki ciepła (m)
Koncepcja oporu cieplnego
W przypadku złożonych geometrii podejście oparte na oporze cieplnym jest często bardziej praktyczne:
R = L/(kA)
Gdzie:
- R = Opór cieplny (K/W)
Dla systemów z wieloma komponentami połączonymi szeregowo:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
A współczynnik przenikania ciepła staje się:
Q = ΔT/Razem
Porównanie przewodności cieplnej materiałów
| Materiał | Przewodność cieplna (W/m-K) | Przewodność względna | Typowe zastosowania |
|---|---|---|---|
| Aluminium | 205-250 | Wysoki | Cylindry, radiatory |
| Stal | 36-54 | Średni | Elementy konstrukcyjne |
| Stal nierdzewna | 14-16 | Niski-średni | Środowiska korozyjne |
| Brąz | 26-50 | Średni | Łożyska, tuleje |
| PTFE | 0.25 | Bardzo niski | Uszczelki, łożyska |
| Kauczuk nitrylowy | 0.13 | Bardzo niski | O-ringi, uszczelki |
| Powietrze (nieruchome) | 0.026 | Bardzo niski | Wypełniacz luk |
| Pasta termoprzewodząca | 3-8 | Niski | Materiał interfejsu |
Rezystancja styku w zespołach pneumatycznych
Na stykach między komponentami rezystancja styku znacząco wpływa na transfer ciepła:
Rcontact = 1/(hc × A)
Gdzie:
- hc = Współczynnik kontaktu (W/m²-K)
- A = powierzchnia styku (m²)
Czynniki wpływające na rezystancję styku obejmują
- Chropowatość powierzchni: Bardziej szorstkie powierzchnie mają mniejszą rzeczywistą powierzchnię styku
- Ciśnienie kontaktowe: Wyższe ciśnienie zwiększa efektywny obszar kontaktu
- Materiały interfejsu: Związki termiczne wypełniają szczeliny powietrzne
- Czystość powierzchni: Zanieczyszczenia mogą zwiększać odporność
Studium przypadku: Optymalizacja termiczna cylindrów beztłoczyskowych
Dla magnetycznego cylindra beztłoczyskowego doświadczającego problemów termicznych:
| Komponent | Oryginalny projekt | Zoptymalizowany projekt | Ulepszenie |
|---|---|---|---|
| Korpus cylindra | Anodowane aluminium | Ten sam materiał, ulepszone wykończenie | 15% lepsze przewodzenie |
| Interfejs łożyska | Kontakt metal-metal | Dodana mieszanka termiczna | 340% lepsze przewodzenie |
| Wsporniki montażowe | Stal malowana | Gołe aluminium | 280% lepsze przewodzenie |
| Ogólna odporność termiczna | 2,8 K/W | 0,7 K/W | Redukcja 75% |
| Temperatura pracy | 78°C | 56°C | Obniżenie o 22°C |
| Żywotność komponentów | 4 miesiące | >12 miesięcy | 3-krotna poprawa |
Praktyczne techniki optymalizacji przewodzenia
Bazując na moim doświadczeniu z setkami systemów pneumatycznych, oto najskuteczniejsze podejścia do poprawy przewodzenia:
Optymalizacja interfejsu
- Wykończenie powierzchni: Poprawa gładkości powierzchni współpracującej do Ra 0,4-0,8 μm
- Materiały interfejsu termicznego2: Zastosowanie odpowiednich związków (3-8 W/m-K)
- Moment dokręcania łącznika: Prawidłowe dokręcenie zapewnia optymalny docisk
- Czystość: Usunąć wszystkie oleje i zanieczyszczenia przed montażem
Strategie wyboru materiałów
- Krytyczne ścieżki ciepła: Używaj materiałów o wysokiej przewodności (aluminium, miedź).
- Przerwy termiczne: Celowe użycie materiałów o niskiej przewodności w celu odizolowania ciepła.
- Podejścia złożone: Łączenie materiałów w celu uzyskania optymalnej wydajności/kosztów
- Materiały anizotropowe: Wykorzystanie przewodności kierunkowej w stosownych przypadkach
Optymalizacja geometryczna
- Długość ścieżki ciepła: Minimalizacja odległości między źródłami ciepła a radiatorami
- Obszar przekroju poprzecznego: Maksymalizacja obszaru prostopadłego do przepływu ciepła
- Termiczne wąskie gardła: Identyfikacja i eliminacja zwężeń na ścieżce ciepła
- Zbędne ścieżki: Tworzenie wielu równoległych ścieżek przewodzenia
Metody poprawy konwekcji: Jakie techniki maksymalizują wymianę ciepła powietrze-powierzchnia?
Konwekcja jest często czynnikiem ograniczającym chłodzenie układów pneumatycznych. Zwiększenie konwekcyjnego transferu ciepła może znacznie poprawić zarządzanie ciepłem i wydajność systemu.
Następuje konwekcyjny transfer ciepła Prawo chłodzenia Newtona3: Q = hA(Ts-T∞), gdzie h to współczynnik konwekcji (W/m²-K), A to pole powierzchni, a (Ts-T∞) to różnica temperatur między powierzchnią a płynem. Metody ulepszania obejmują zwiększanie powierzchni poprzez żebra, poprawę prędkości płynu za pomocą ukierunkowanego przepływu powietrza oraz optymalizację właściwości powierzchni w celu promowania turbulentnych warstw granicznych.
Podczas audytu efektywności energetycznej w zakładzie pakowania w Arizonie natknąłem się na system pneumatyczny działający w środowisku o temperaturze otoczenia 43°C. Ich beztłoczyskowe cylindry przegrzewały się, mimo że spełniały wszystkie wymagania konserwacyjne. Wdrażając ukierunkowaną poprawę konwekcji - dodając małe aluminiowe żebra i wentylator o niskiej mocy - zwiększyliśmy współczynnik konwekcji o 450%. Obniżyło to temperaturę roboczą z niebezpiecznego poziomu do wartości zgodnej ze specyfikacją bez żadnych większych modyfikacji systemu.
Podstawy konwekcyjnego przenoszenia ciepła
Podstawowe równanie regulujące konwekcyjną wymianę ciepła to:
Q = hA(Ts-T∞)
Gdzie:
- Q = Współczynnik przenikania ciepła (W)
- h = Współczynnik konwekcji (W/m²-K)
- A = Powierzchnia (m²)
- Ts = Temperatura powierzchni (K)
- T∞ = Temperatura płynu (powietrza) (K)
Współczynnik konwekcji h zależy od wielu czynników:
- Właściwości płynu (gęstość, lepkość, przewodność cieplna)
- Charakterystyka przepływu (prędkość, turbulencje)
- Geometria i orientacja powierzchni
- Reżim przepływu (konwekcja naturalna vs. wymuszona)
Konwekcja naturalna a wymuszona
| Parametr | Konwekcja naturalna | Konwekcja wymuszona | Skutki |
|---|---|---|---|
| Typowa wartość h | 5-25 W/m²-K | 25-250 W/m²-K | Wymuszona konwekcja może być 10 razy bardziej efektywna |
| Siła napędowa | Pływalność (różnica temperatur) | Ciśnienie zewnętrzne (wentylatory, dmuchawy) | Konwekcja wymuszona jest mniej zależna od temperatury |
| Wzór przepływu | Pionowy przepływ wzdłuż powierzchni | Kierunek oparty na mechanizmie wymuszania | Wymuszony przepływ można zoptymalizować pod kątem określonych komponentów |
| Niezawodność | Pasywny, zawsze obecny | Wymaga zasilania i konserwacji | Naturalna konwekcja zapewnia podstawowe chłodzenie |
| Wymagania dotyczące przestrzeni | Wymaga wolnej przestrzeni dla cyrkulacji powietrza | Wymaga miejsca na klimatyzatory i kanały wentylacyjne | Systemy wymuszone wymagają więcej planowania |
Techniki poprawy konwekcji
Zwiększenie powierzchni
Zwiększenie efektywnej powierzchni poprzez:
Płetwy i rozszerzone powierzchnie
- Płetwy pinowe: Wielokierunkowy przepływ powietrza, zwiększenie powierzchni 150-300%
- Płytowe żebra: Kierunkowy przepływ powietrza, zwiększenie powierzchni 200-500%
- Powierzchnie faliste: Umiarkowane wzmocnienie, wzrost powierzchni 50-150%Szorstkowanie powierzchni
- Mikroteksturowanie: 5-15% efektywny wzrost powierzchni
- Wgłębione powierzchnie: wzrost 10-30% plus efekty warstwy granicznej
- Rowkowane wzory: 15-40% zwiększają korzyści kierunkowe
Manipulacja przepływem
Poprawa charakterystyki przepływu powietrza poprzez:
Systemy wymuszonego obiegu powietrza
- Wentylatory: kierunkowy przepływ powietrza, 200-600% h improvement
- Dmuchawy: Przepływ pod wysokim ciśnieniem, 300-800% h poprawa
- Strumienie sprężonego powietrza: Ukierunkowane chłodzenie, 400-1000% lokalna poprawa hOptymalizacja ścieżki przepływu
- Przegrody: Kierują powietrze do krytycznych podzespołów
- Efekty Venturiego: Przyspieszenie powietrza na określonych powierzchniach
- Generatory wirów: Tworzenie turbulencji w celu zakłócenia warstwy granicznej
Modyfikacje powierzchni
Zmiana właściwości powierzchni w celu zwiększenia konwekcji:
Obróbka emisyjności
- Czarny tlenek: Zwiększa emisyjność do 0,7-0,9
- Anodowanie: Kontrolowana emisyjność od 0,4-0,9
- Farby i powłoki: Możliwość dostosowania emisyjności do 0,98Kontrola zwilżalności
- Powłoki hydrofilowe: Lepsze chłodzenie cieczą
- Powierzchnie hydrofobowe: Zapobiegają kondensacji pary wodnej
- Wzorcowa zwilżalność: Ukierunkowany przepływ kondensatu
Praktyczny przykład wdrożenia
Do beztłoczyskowego siłownika pneumatycznego pracującego w środowisku o wysokiej temperaturze:
| Metoda ulepszania | Wdrożenie | h Poprawa | Redukcja temperatury |
|---|---|---|---|
| Pin Fins (6 mm) | Aluminiowe płetwy zatrzaskowe, rozstaw 10 mm | 180% | 12°C |
| Ukierunkowany przepływ powietrza | Wentylator 80 mm, 2 W DC przy prędkości 1,5 m/s | 320% | 18°C |
| Obróbka powierzchni | Anodowanie na czarno | 40% | 3°C |
| Podejście łączone | Wszystkie metody zintegrowane | 450% | 24°C |
Korelacja liczby Nusselta dla obliczeń projektowych
W przypadku obliczeń inżynierskich Liczba Nusselta4 (Nu) zapewnia bezwymiarowe podejście do konwekcji:
Nu = hL/k
Gdzie:
- L = Długość charakterystyczna
- k = Przewodność cieplna płynu
Dla konwekcji wymuszonej nad płaską płytą:
Nu = 0,664Re^(1/2)Pr^(1/3) (przepływ laminarny)
Nu = 0,037Re^(4/5)Pr^(1/3) (przepływ turbulentny)
Gdzie:
- Re = liczba Reynoldsa (prędkość × długość × gęstość / lepkość)
- Pr = liczba Prandtla (ciepło właściwe × lepkość / przewodność cieplna)
Korelacje te pozwalają inżynierom przewidywać współczynniki konwekcji dla różnych konfiguracji i odpowiednio optymalizować strategie chłodzenia.
Model efektywności promieniowania: Kiedy promieniowanie cieplne ma znaczenie w układach pneumatycznych?
Promieniowanie jest często pomijane w zarządzaniu ciepłem w układach pneumatycznych, ale może odpowiadać za 15-30% całkowitego transferu ciepła w wielu zastosowaniach. Zrozumienie, kiedy i jak zoptymalizować radiacyjne przenoszenie ciepła ma kluczowe znaczenie dla kompleksowego zarządzania ciepłem.
Promieniowanie cieplne jest zgodne z Prawo Stefana-Boltzmanna5: Q = εσA(T₁⁴-T₂⁴), gdzie ε to emisyjność powierzchni, σ to stała Stefana-Boltzmanna, A to pole powierzchni, a T₁ i T₂ to temperatury bezwzględne powierzchni emitującej i otoczenia. Wydajność promieniowania w układach pneumatycznych zależy przede wszystkim od emisyjności powierzchni, różnicy temperatur i czynników widzenia między komponentami a ich otoczeniem.
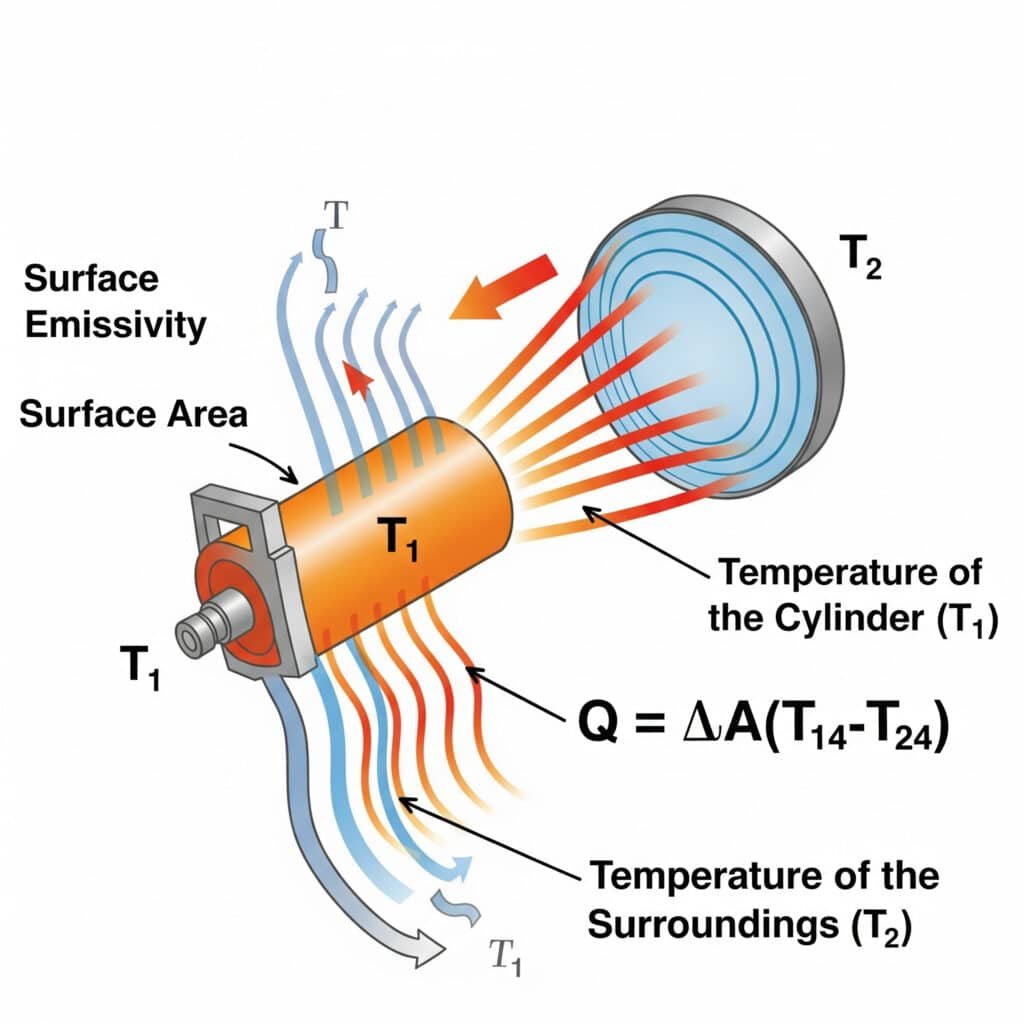
Niedawno pomogłem producentowi sprzętu półprzewodnikowego z Oregonu rozwiązać problem przegrzewania się precyzyjnych cylindrów beztłoczyskowych. Inżynierowie skupili się wyłącznie na przewodzeniu i konwekcji, ale przeoczyli promieniowanie. Stosując powłokę o wysokiej emisyjności (zwiększając ε z 0,11 do 0,92), poprawiliśmy radiacyjny transfer ciepła o ponad 700%. To proste, pasywne rozwiązanie obniżyło temperaturę roboczą o 9°C bez żadnych ruchomych części ani zużycia energii - co jest krytycznym wymogiem w środowisku pomieszczeń czystych.
Podstawy wymiany ciepła przez promieniowanie
Podstawowym równaniem rządzącym radiacyjnym przenoszeniem ciepła jest:
Q = εσA(T₁⁴-T₂⁴)
Gdzie:
- Q = Współczynnik przenikania ciepła (W)
- ε = emisyjność (bezwymiarowa, 0-1)
- σ = stała Stefana-Boltzmanna (5,67 × 10-⁸ W/m²-K⁴)
- A = Powierzchnia (m²)
- T₁ = temperatura bezwzględna powierzchni (K)
- T₂ = temperatura bezwzględna otoczenia (K)
Wartości emisyjności powierzchni dla popularnych materiałów pneumatycznych
| Materiał/powierzchnia | Emisyjność (ε) | Efektywność promieniowania | Potencjał ulepszeń |
|---|---|---|---|
| Polerowane aluminium | 0.04-0.06 | Bardzo słaby | Możliwa poprawa >1500% |
| Anodowane aluminium | 0.7-0.9 | Doskonały | Już zoptymalizowane |
| Stal nierdzewna (polerowana) | 0.07-0.14 | Słaby | Możliwa poprawa >600% |
| Stal nierdzewna (oksydowana) | 0.6-0.85 | Dobry | Możliwa umiarkowana poprawa |
| Stal (polerowana) | 0.07-0.10 | Słaby | Możliwa poprawa >900% |
| Stal (oksydowana) | 0.7-0.9 | Doskonały | Już zoptymalizowane |
| Malowane powierzchnie | 0.8-0.98 | Doskonały | Już zoptymalizowane |
| PTFE (biały) | 0.8-0.9 | Doskonały | Już zoptymalizowane |
| Kauczuk nitrylowy | 0.86-0.94 | Doskonały | Już zoptymalizowane |
Wyświetlanie czynników
Wymiana promieniowania zależy nie tylko od emisyjności, ale także od geometrycznych relacji między powierzchniami:
F₁₂ = część promieniowania opuszczającego powierzchnię 1, która uderza w powierzchnię 2
W przypadku złożonych geometrii współczynniki widoku można obliczyć za pomocą:
- Rozwiązania analityczne dla prostych geometrii
- Zobacz algebrę współczynników do łączenia znanych rozwiązań
- Metody numeryczne dla złożonych układów
- Przybliżenia empiryczne dla inżynierii praktycznej
Zależność promieniowania od temperatury
Zależność temperatury od czwartej potęgi sprawia, że promieniowanie jest szczególnie skuteczne w wyższych temperaturach:
| Temperatura powierzchni | Procent wymiany ciepła przez promieniowanie* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Zakładając warunki konwekcji naturalnej, ε = 0,8, 25°C otoczenia
Strategie poprawy efektywności promieniowania
Opierając się na moim doświadczeniu z przemysłowymi systemami pneumatycznymi, oto najskuteczniejsze podejścia do poprawy wymiany ciepła przez promieniowanie:
Modyfikacja emisyjności powierzchni
Powłoki o wysokiej emisyjności
- Czarne anodowanie aluminium (ε ≈ 0,8-0,9)
- Czarny tlenek dla stali (ε ≈ 0,7-0,8)
- Specjalistyczne powłoki ceramiczne (ε ≈ 0,9-0,98)Teksturowanie powierzchni
- Mikroszorstkowanie zwiększa efektywną emisyjność
- Porowate powierzchnie poprawiają właściwości radiacyjne
- Połączone ulepszenia emisyjności/konwekcji
Optymalizacja środowiskowa
Zarządzanie temperaturą otoczenia
- Osłona przed gorącym sprzętem/procesami
- Chłodne ściany/sufity dla lepszej wymiany promieniowania
- Bariery odblaskowe kierujące promieniowanie na chłodniejsze powierzchnieView Factor Improvement
- Orientacja w celu zmaksymalizowania ekspozycji na chłodne powierzchnie
- Usuwanie blokujących obiektów
- Reflektory poprawiające wymianę promieniowania z chłodniejszymi obszarami
Studium przypadku: Wzmocnienie promieniowania w pneumatyce precyzyjnej
Do precyzyjnych siłowników beztłoczyskowych w pomieszczeniach czystych:
| Parametr | Oryginalny projekt | Konstrukcja wzmocniona promieniowaniem | Ulepszenie |
|---|---|---|---|
| Materiał powierzchni | Polerowane aluminium (ε ≈ 0,06) | Aluminium z powłoką ceramiczną (ε ≈ 0,94) | 1467% wzrost emisyjności |
| Promieniowanie cieplne | 2.1W | 32.7W | 1457% wzrost promieniowania |
| Temperatura pracy | 68°C | 59°C | Redukcja o 9°C |
| Żywotność komponentów | 8 miesięcy | >24 miesiące | 3-krotna poprawa |
| Koszt wdrożenia | – | $175 na cylinder | 4,2 miesiąca zwrotu z inwestycji |
Promieniowanie a inne tryby wymiany ciepła
Zrozumienie, kiedy promieniowanie dominuje, ma kluczowe znaczenie dla efektywnego zarządzania temperaturą:
| Stan | Dominacja przewodzenia | Dominacja konwekcji | Dominacja promieniowania |
|---|---|---|---|
| Zakres temperatur | Niski do wysokiego | Niski do średniego | Średni do wysokiego |
| Właściwości materiału | Materiały wysokiej jakości | Niskie k, duża powierzchnia | Powierzchnie o wysokim ε |
| Czynniki środowiskowe | Dobry kontakt termiczny | Ruch powietrza, wentylatory | Duża różnica temperatur |
| Ograniczenia przestrzenne | Szczelne opakowanie | Otwarty przepływ powietrza | Widok na chłodniejsze otoczenie |
| Najlepsze aplikacje | Interfejsy komponentów | Chłodzenie ogólne | Gorące powierzchnie, próżnia, nieruchome powietrze |
Wnioski
Opanowanie zasad wymiany ciepła - obliczania współczynnika przewodzenia, metod zwiększania konwekcji i modelowania wydajności promieniowania - stanowi podstawę skutecznego zarządzania temperaturą w układach pneumatycznych. Stosując te zasady, można obniżyć temperaturę pracy, wydłużyć żywotność komponentów i poprawić efektywność energetyczną, zapewniając jednocześnie niezawodne działanie nawet w trudnych warunkach.
Najczęściej zadawane pytania dotyczące wymiany ciepła w układach pneumatycznych
Jaki jest typowy wzrost temperatury w siłownikach pneumatycznych podczas pracy?
Siłowniki pneumatyczne zazwyczaj doświadczają wzrostu temperatury o 20-40°C powyżej temperatury otoczenia podczas ciągłej pracy. Wzrost ten wynika z tarcia między uszczelkami i ściankami cylindra, sprężania powietrza i pracy mechanicznej przekształcanej w ciepło. Cylindry beztłoczyskowe często doświadczają wyższych wzrostów temperatury (30-50°C) ze względu na ich bardziej złożone systemy uszczelnień i skoncentrowane wytwarzanie ciepła w zespole łożysko/uszczelka.
Jak ciśnienie robocze wpływa na wytwarzanie ciepła w układach pneumatycznych?
Ciśnienie robocze ma znaczący wpływ na wytwarzanie ciepła, przy czym wyższe ciśnienie wytwarza więcej ciepła poprzez kilka mechanizmów. Każdy wzrost ciśnienia roboczego o 1 bar zazwyczaj zwiększa wytwarzanie ciepła o 8-12% ze względu na większe siły tarcia między uszczelkami i powierzchniami, wyższe nagrzewanie sprężania i zwiększone straty związane z wyciekami. Zależność ta jest w przybliżeniu liniowa w normalnych zakresach roboczych (3-10 barów).
Jakie jest optymalne podejście do chłodzenia komponentów pneumatycznych w różnych środowiskach?
Optymalne podejście do chłodzenia różni się w zależności od środowiska: w czystych środowiskach o umiarkowanej temperaturze (15-30°C) często wystarcza naturalna konwekcja z odpowiednimi odstępami między komponentami. W środowiskach o wysokiej temperaturze (30-50°C) konieczna staje się konwekcja wymuszona przy użyciu wentylatorów lub sprężonego powietrza. W ekstremalnie gorących warunkach (>50°C) lub gdy przepływ powietrza jest ograniczony, wymagane mogą być aktywne metody chłodzenia, takie jak chłodnice termoelektryczne lub chłodzenie cieczą. We wszystkich przypadkach maksymalizacja promieniowania przez powierzchnie o wysokiej emisyjności zapewnia dodatkowe chłodzenie pasywne.
Jak obliczyć całkowity transfer ciepła z elementu pneumatycznego?
Oblicz całkowity transfer ciepła, sumując wkład każdego z mechanizmów: Qtotal = Qconduction + Qconvection + Qradiation. W przypadku przewodzenia należy użyć Q = kA(T₁-T₂)/L dla każdej ścieżki ciepła. W przypadku konwekcji należy użyć Q = hA(Ts-T∞) z odpowiednimi współczynnikami konwekcji. W przypadku promieniowania należy użyć Q = εσA(T₁⁴-T₂⁴). W większości przemysłowych zastosowań pneumatycznych działających w temperaturze 30-80°C, przybliżony rozkład wynosi 20-40% przewodzenia, 40-70% konwekcji i 10-30% promieniowania.
Jaki jest związek między temperaturą a żywotnością podzespołów pneumatycznych?
Żywotność podzespołów spada wykładniczo wraz ze wzrostem temperatury, zgodnie ze zmodyfikowaną zależnością Arrheniusa. Z reguły każde 10°C wzrostu temperatury roboczej zmniejsza żywotność uszczelnienia i komponentu o 40-50%. Oznacza to, że komponent działający w temperaturze 70°C może działać tylko o jedną trzecią dłużej niż ten sam komponent w temperaturze 50°C. Zależność ta jest szczególnie istotna w przypadku komponentów polimerowych, takich jak uszczelki, łożyska i uszczelnienia, które często określają częstotliwość konserwacji systemów pneumatycznych.
-
Zawiera podstawowe wyjaśnienie prawa Fouriera, fundamentalnej zasady opisującej sposób przewodzenia ciepła przez materiały stałe w oparciu o ich przewodność cieplną i gradient temperatury. ↩
-
Wyjaśnia funkcje i rodzaje materiałów interfejsu termicznego (TIM), które są używane do wypełniania mikroskopijnych szczelin powietrznych między komponentami w celu poprawy przewodzenia ciepła i zmniejszenia oporu cieplnego. ↩
-
Szczegółowe informacje na temat prawa chłodzenia Newtona, które reguluje sposób chłodzenia obiektów poprzez przenoszenie ciepła do otaczającego płynu poprzez konwekcję, co jest kluczowym czynnikiem w projektowaniu chłodzenia systemu. ↩
-
Oferuje dogłębne spojrzenie na liczbę Nusselta, krytyczną bezwymiarową wielkość w dynamice płynów i przenoszeniu ciepła, która reprezentuje stosunek konwekcyjnego do przewodzącego przenoszenia ciepła przez granicę. ↩
-
Opisuje prawo Stefana-Boltzmanna, podstawową zasadę fizyczną, która określa ilościowo całkowitą energię wypromieniowaną przez ciało czarne, co jest niezbędne do obliczania strat ciepła z gorących powierzchni. ↩


