Fizyka stojąca za siłownikami obrotowymi typu łopatkowego obejmuje złożone interakcje między dynamiką płynów, siłami mechanicznymi i termodynamiką, których większość inżynierów nigdy w pełni nie zrozumie. Jednak opanowanie tych zasad ma kluczowe znaczenie dla optymalizacji wydajności, przewidywania zachowania i rozwiązywania wyzwań związanych z aplikacjami, które mogą wpłynąć na projekt lub go zepsuć. 🔬
Siłowniki obrotowe typu łopatkowego działają w oparciu o zasadę zwielokrotniania ciśnienia Pascala, przekształcając liniową siłę pneumatyczną w obrotowy moment obrotowy za pomocą mechanizmów ślizgowych łopatek, przy czym wydajność jest regulowana przez różnice ciśnień, geometrię łopatek, współczynniki tarcia i termodynamiczne prawa gazowe, które określają wyjściowy moment obrotowy, prędkość i charakterystykę wydajności.
Niedawno współpracowałem z inżynierem projektantem o imieniu Jennifer w zakładzie produkcji lotniczej w Seattle, który zmagał się z niespójnością momentu obrotowego w aplikacji siłownika obrotowego. Jej siłowniki wytwarzały o 30% mniejszy moment obrotowy niż obliczono, powodując błędy pozycjonowania w krytycznych operacjach montażowych. Podstawowa przyczyna nie była mechaniczna - było nią fundamentalne niezrozumienie fizyki rządzącej zachowaniem siłownika łopatkowego. ✈️
Spis treści
- W jaki sposób dynamika ciśnienia generuje moment obrotowy w siłownikach łopatkowych?
- Jaką rolę odgrywa geometria łopatek w określaniu charakterystyki działania siłownika?
- Jakie zasady termodynamiki wpływają na prędkość i wydajność siłownika obrotowego?
- Jak siły tarcia i straty mechaniczne wpływają na wydajność siłownika w świecie rzeczywistym?
W jaki sposób dynamika ciśnienia generuje moment obrotowy w siłownikach łopatkowych?
Zrozumienie konwersji ciśnienia na moment obrotowy ma fundamentalne znaczenie dla projektowania i stosowania siłowników obrotowych.
Siłowniki łopatkowe generują moment obrotowy poprzez różnice ciśnień działające na powierzchnie łopatek, gdzie moment obrotowy jest równy różnicy ciśnień razy efektywna powierzchnia łopatek razy moment obrotowy. ramię momentowe1 odległość, z zależnością T = ΔP × A × r, zmodyfikowaną przez kąt łopatek i geometrię komory w celu wytworzenia ruchu obrotowego z liniowych sił pneumatycznych.
Podstawowe zasady generowania momentu obrotowego
Zastosowanie zasady Pascala
Podstawą działania siłownika obrotowego jest Zasada Pascala2:
- Przekładnia ciśnieniowa: Jednolite ciśnienie działa na wszystkie powierzchnie w komorze
- Mnożenie sił: Ciśnienie × powierzchnia = siła na każdej powierzchni łopatki
- Tworzenie chwili: Siła × promień = moment obrotowy wokół osi centralnej
Podstawy obliczania momentu obrotowego
Podstawowy wzór na moment obrotowy: T = ΔP × A_eff × r_eff × η
Gdzie:
- T = wyjściowy moment obrotowy (lb-in)
- ΔP = Różnica ciśnień (PSI)
- A_eff = efektywna powierzchnia łopatki (cal kwadratowy)
- r_eff = efektywne ramię momentu (cale)
- η = sprawność mechaniczna (0,85-0,95)
Analiza rozkładu ciśnienia
Dynamika ciśnienia w komorze
Rozkład ciśnienia w komorach łopatkowych nie jest równomierny:
- Komora wysokociśnieniowa: Ciśnienie zasilania minus straty przepływu
- Komora niskociśnieniowa: Ciśnienie wylotowe plus przeciwciśnienie
- Strefy przejściowe: Gradienty ciśnienia na krawędziach łopatek
- Martwe tomy: Uwięzione powietrze w wolnej przestrzeni
Obliczenia powierzchni efektywnej
| Konfiguracja łopatek | Wzór na efektywny obszar | Współczynnik wydajności |
|---|---|---|
| Pojedyncza łopatka | A = L × W × sin(θ) | 0.85-0.90 |
| Podwójna łopatka | A = 2 × L × W × sin(θ/2) | 0.88-0.93 |
| Multi-Vane | A = n × L × W × sin(θ/n) | 0.90-0.95 |
Gdzie L = długość łopatki, W = szerokość łopatki, θ = kąt obrotu, n = liczba łopatek
Efekty ciśnienia dynamicznego
Straty ciśnienia wywołane przepływem
Dynamika ciśnienia w świecie rzeczywistym obejmuje straty związane z przepływem:
- Ograniczenia wlotu: Spadki ciśnienia zaworów i złączek
- Wewnętrzne straty przepływu: Turbulencje i tarcie w komorach
- Ograniczenia wydechu: Przeciwciśnienie z układów wydechowych
- Straty przyspieszenia: Ciśnienie wymagane do przyspieszenia poruszającego się powietrza
Aplikacja lotnicza Jennifer cierpiała z powodu nieodpowiedniego doboru przewodów zasilających, co powodowało spadek ciśnienia o 15 PSI podczas szybkich ruchów siłownika. Ta strata ciśnienia, w połączeniu z dynamicznymi efektami przepływu, wyjaśniała redukcję momentu obrotowego 30%, której doświadczała. 📉
Jaką rolę odgrywa geometria łopatek w określaniu charakterystyki działania siłownika?
Geometria łopatek ma bezpośredni wpływ na wyjściowy moment obrotowy, kąt obrotu, prędkość i charakterystykę wydajności.
Geometria łopatki określa wydajność siłownika poprzez długość łopatki (wpływa na ramię momentu obrotowego), szerokość (określa obszar ciśnienia), grubość (wpływa na uszczelnienie i tarcie), zależności kątowe (kontroluje zakres obrotu) i specyfikacje luzu (wpływa na wyciek i wydajność), przy czym każdy parametr wymaga optymalizacji pod kątem konkretnych zastosowań.
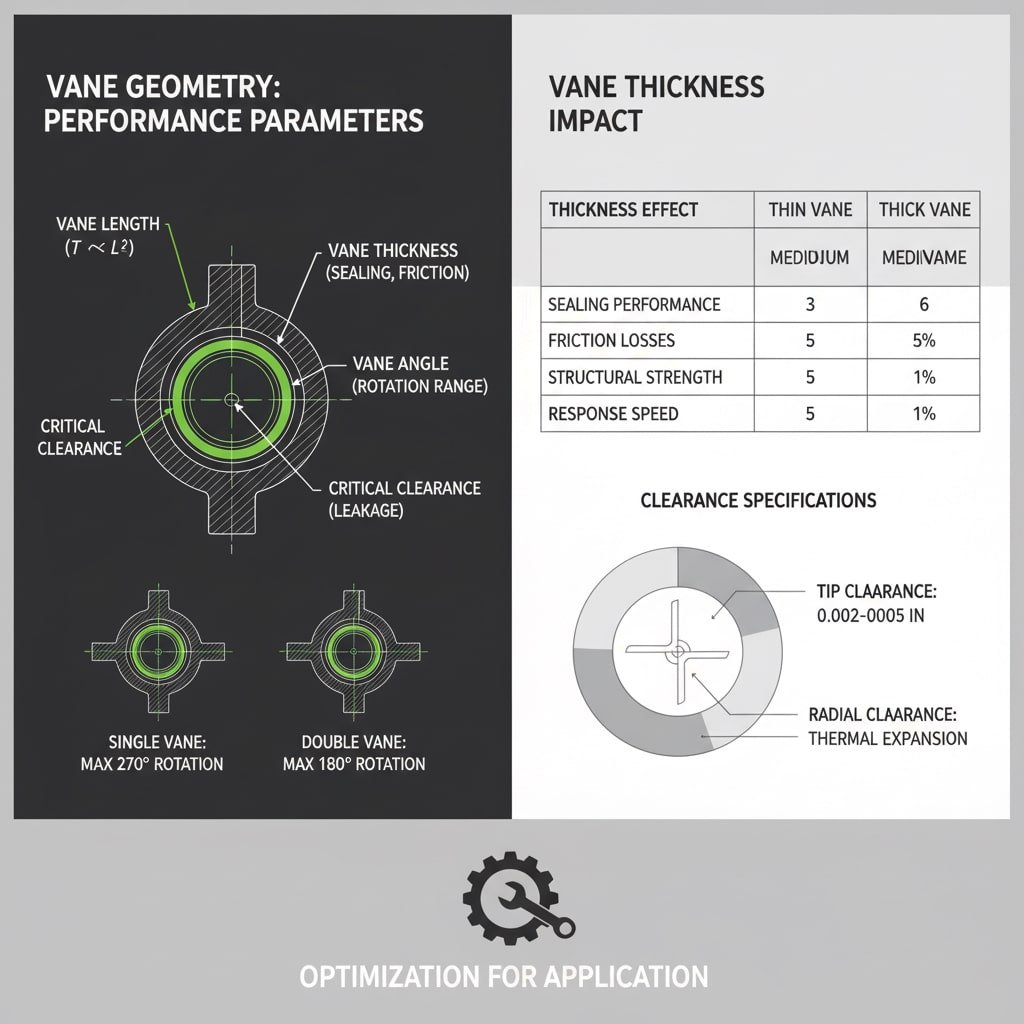
Analiza parametrów geometrycznych
Optymalizacja długości łopatek
Długość łopatek ma bezpośredni wpływ na moment obrotowy i integralność strukturalną:
- Zależność momentu obrotowego: T ∝ L² (zależność kwadratu długości)
- Rozważania dotyczące stresu: Naprężenie zginające rośnie wraz ze wzrostem długości
- Efekty odchylenia: Dłuższe łopatki mają większe ugięcie końcówki
- Optymalne proporcje: Stosunek długości do szerokości wynoszący od 3:1 do 5:1 zapewnia najlepszą wydajność.
Wpływ grubości łopatki
Grubość łopatek wpływa na wiele parametrów wydajności:
| Efekt grubości | Cienkie łopatki (< 0,25″) | Średnie łopatki (0,25″-0,5″) | Grube łopatki (> 0,5″) |
|---|---|---|---|
| Wydajność uszczelniania | Słaby - wysoki wyciek | Dobry - odpowiedni kontakt | Doskonałe - szczelne uszczelnienia |
| Straty tarcia | Niski | Średni | Wysoki |
| Wytrzymałość strukturalna | Słaby - problemy z odchylaniem | Dobra - odpowiednia sztywność | Doskonały - sztywny |
| Szybkość reakcji | Szybko | Średni | Powolny |
Rozważania dotyczące geometrii kątowej
Ograniczenia kąta obrotu
Geometria łopatek ogranicza maksymalne kąty obrotu:
- Pojedyncza łopatka: Maksymalny obrót ~270°
- Podwójna łopatka: Maksymalny obrót ~180
- Wielołopatkowy: Obrót ograniczony przez interferencję łopatek
- Konstrukcja komory: Geometria obudowy wpływa na użyteczny kąt
Optymalizacja kąta łopatek
Kąt pomiędzy łopatkami wpływa na charakterystykę momentu obrotowego:
- Równe odstępy: Zapewnia płynne dostarczanie momentu obrotowego
- Nierówne odstępy: Możliwość optymalizacji krzywych momentu obrotowego dla określonych zastosowań
- Kąty progresywne: Kompensacja zmian ciśnienia
Geometria prześwitu i uszczelnienia
Specyfikacje prześwitu krytycznego
Odpowiednie luzy równoważą skuteczność uszczelnienia z tarciem:
- Usuwanie wskazówek: 0,002″-0,005″ dla optymalnego uszczelnienia
- Prześwit boczny: 0,001″-0,003″, aby zapobiec wiązaniu
- Luz promieniowy: Rozważania dotyczące rozszerzalności temperaturowej
- Luz osiowy: Łożysko oporowe i wzrost temperatury
W Bepto nasz proces optymalizacji geometrii łopatek wykorzystuje obliczeniowa dynamika płynów (CFD)3 analiza połączona z testami empirycznymi w celu osiągnięcia idealnej równowagi między momentem obrotowym, prędkością i wydajnością dla każdego zastosowania. Takie podejście inżynieryjne pozwoliło nam osiągnąć wydajność o 15-20% wyższą niż w przypadku standardowych konstrukcji. 🔧
Jakie zasady termodynamiki wpływają na prędkość i wydajność siłownika obrotowego?
Efekty termodynamiczne mają znaczący wpływ na wydajność siłownika, zwłaszcza w zastosowaniach wymagających dużej prędkości lub dużych obciążeń.
Zasady termodynamiki wpływające na siłowniki obrotowe obejmują rozprężanie i sprężanie gazu podczas obrotu, wytwarzanie ciepła w wyniku tarcia i spadków ciśnienia, wpływ temperatury na gęstość i lepkość powietrza oraz procesy adiabatyczne i izotermiczne, które określają rzeczywistą i teoretyczną wydajność w rzeczywistych warunkach pracy.

Zastosowania prawa gazowego
Efekty prawa gazu doskonałego
Wydajność siłownika obrotowego jest zgodna z prawem gazu:
- Praca w trybie ciśnieniowo-objętościowym: W = ∫P dV podczas ekspansji
- Wpływ temperatury: PV = nRT reguluje zależności ciśnienie-temperatura
- Zmiany gęstości: ρ = PM/RT wpływa na obliczenia przepływu masowego
- Ściśliwość: Efekty gazu rzeczywistego przy wysokich ciśnieniach
Procesy adiabatyczne a izotermiczne
Działanie siłownika obejmuje oba typy procesów:
| Typ procesu | Charakterystyka | Wpływ na wydajność |
|---|---|---|
| Adiabatyczny | Brak wymiany ciepła, szybka ekspansja | Wyższe spadki ciśnienia, zmiany temperatury |
| Izotermiczny | Stała temperatura, powolne rozszerzanie | Bardziej wydajna konwersja energii |
| Polytropic | Połączenie w świecie rzeczywistym | Rzeczywista wydajność pomiędzy skrajnościami |
Wytwarzanie i przenoszenie ciepła
Ogrzewanie wywołane tarciem
Wiele źródeł generuje ciepło w siłownikach obrotowych:
- Tarcie końcówki łopatki: Kontakt ślizgowy z obudową
- Tarcie łożyska: Ubytki łożyska podporowego wału
- Tarcie uszczelki: Siły oporu uszczelnienia obrotowego
- Tarcie płynów: Straty lepkości w przepływie powietrza
Obliczenia wzrostu temperatury
Szybkość wytwarzania ciepła: Q = μ × N × F × V
Gdzie:
- Q = wytwarzanie ciepła (BTU/godz.)
- μ = Współczynnik tarcia
- N = Prędkość obrotowa (RPM)
- F = Siła normalna (funty)
- V = prędkość przesuwu (ft/min)
Analiza wydajności
Współczynniki wydajności termodynamicznej
Ogólna wydajność łączy w sobie wiele mechanizmów strat:
- Wydajność objętościowa: ηv = przepływ rzeczywisty / przepływ teoretyczny
- Wydajność mechaniczna: ηm = moc wyjściowa / moc wejściowa
- Ogólna wydajność: ηo = ηv × ηm
Strategie optymalizacji wydajności
| Strategia | Wzrost wydajności | Koszt wdrożenia |
|---|---|---|
| Ulepszone uszczelnienie | 5-15% | Średni |
| Zoptymalizowane prześwity | 3-8% | Niski |
| Zaawansowane materiały | 8-12% | Wysoki |
| Zarządzanie ciepłem | 5-10% | Średni |
Dynamika przepływu i straty ciśnienia
Wpływ liczby Reynoldsa
Charakterystyka przepływu zmienia się w zależności od warunków pracy:
- Przepływ laminarny: Re < 2300, przewidywalne straty ciśnienia
- Przepływ turbulentny: Re > 4000, wyższe współczynniki tarcia
- Region przejściowy: Nieprzewidywalna charakterystyka przepływu
Analiza termodynamiczna wykazała, że aplikacja lotnicza Jennifer doświadczała znacznego wzrostu temperatury podczas szybkich cykli, co zmniejszyło gęstość powietrza o 12% i przyczyniło się do utraty momentu obrotowego. Wdrożyliśmy strategie zarządzania temperaturą, które przywróciły pełną wydajność. 🌡️
Jak siły tarcia i straty mechaniczne wpływają na wydajność siłownika w świecie rzeczywistym?
Tarcie i straty mechaniczne znacznie zmniejszają teoretyczną wydajność i muszą być starannie zarządzane w celu zapewnienia optymalnego działania siłownika.
Straty mechaniczne w siłownikach łopatkowych obejmują tarcie ślizgowe na końcówkach łopatek, opór uszczelnienia obrotowego, tarcie łożyska i wewnętrzne turbulencje powietrza, zwykle zmniejszające teoretyczny moment obrotowy o 10-20% i wymagające starannego doboru materiałów, obróbki powierzchni i strategii smarowania w celu zminimalizowania pogorszenia wydajności.
Analiza i modelowanie tarcia
Mechanizmy tarcia końcówki łopatki
Główne źródło tarcia występuje na styku obudowy z obudową:
- Smarowanie graniczne: Bezpośredni kontakt metal-metal
- Smarowanie mieszane: Częściowa separacja warstwy płynu
- Smarowanie hydrodynamiczne: Pełny film płynu (rzadkość w pneumatyce)
Zmiany współczynnika tarcia
| Kombinacja materiałów | Tarcie na sucho (μ) | Tarcie smarowane (μ) | Wrażliwość na temperaturę |
|---|---|---|---|
| Stal na stali | 0.6-0.8 | 0.1-0.15 | Wysoki |
| Stal na brązie | 0.3-0.5 | 0.08-0.12 | Średni |
| Stal na PTFE | 0.1-0.2 | 0.05-0.08 | Niski |
| Powłoka ceramiczna | 0.2-0.3 | 0.06-0.10 | Bardzo niski |
Analiza strat w łożyskach
Tarcie łożyska promieniowego
Łożyska wału wyjściowego przyczyniają się do znacznych strat:
- Tarcie toczne: Fr = μr × N × r
- Tarcie ślizgowe: Fs = μs × N
- Tarcie lepkie: Fv = η × A × V/h
- Tarcie uszczelki: Dodatkowy opór powodowany przez uszczelnienia wału
Wpływ wyboru łożyska
Różne typy łożysk wpływają na ogólną wydajność:
- Łożyska kulkowe: Niskie tarcie, wysoka precyzja
- Łożyska wałeczkowe: Wyższa nośność, umiarkowane tarcie
- Łożyska ślizgowe: Wysokie tarcie, prosta konstrukcja
- Łożyska magnetyczne: Tarcie bliskie zeru, wysoki koszt
Rozwiązania inżynierii powierzchni
Zaawansowana obróbka powierzchni
Nowoczesna obróbka powierzchni znacznie zmniejsza tarcie:
- Twarde chromowanie: Zmniejsza zużycie, umiarkowana redukcja tarcia
- Powłoki ceramiczne: Doskonała odporność na zużycie, niskie tarcie
- Węgiel diamentopodobny (DLC): Bardzo niskie tarcie, drogie
- Specjalistyczne polimery: Rozwiązania specyficzne dla aplikacji
Strategie smarowania
| Metoda smarowania | Redukcja tarcia | Wymagania dotyczące konserwacji | Wpływ na koszty |
|---|---|---|---|
| Systemy mgły olejowej | 60-80% | Wysoki - regularne uzupełnianie | Wysoki |
| Smary stałe | 40-60% | Niska - długa żywotność | Średni |
| Materiały samosmarujące | 50-70% | Bardzo niski - stały | Wysoka wartość początkowa |
| Suche środki smarne | 30-50% | Średni - okresowe ponowne zastosowanie | Niski |
Strategie optymalizacji wydajności
Zintegrowane podejście do projektowania
W Bepto optymalizujemy tarcie poprzez systematyczne projektowanie:
- Wybór materiału: Kompatybilne pary materiałów
- Wykończenie powierzchni: Zoptymalizowana chropowatość dla każdego zastosowania
- Kontrola prześwitu: Minimalizacja siły nacisku
- Zarządzanie ciepłem: Kontrola rozszerzalności pod wpływem temperatury
Weryfikacja wydajności w świecie rzeczywistym
Testy laboratoryjne często różnią się od wydajności w terenie:
- Efekty docierania: Wydajność poprawia się wraz z początkowym uruchomieniem
- Wpływ zanieczyszczenia: Rzeczywiste efekty brudu i zanieczyszczeń
- Cykliczne zmiany temperatury: Rozszerzalność cieplna i kurczliwość
- Zmiany obciążenia: Obciążenie dynamiczne a warunki testu statycznego
Nasz kompleksowy program analizy i optymalizacji tarcia pomógł aplikacji lotniczej Jennifer osiągnąć 95% teoretycznego momentu obrotowego - znaczną poprawę w stosunku do pierwotnych 70%. Kluczem było wdrożenie wieloaspektowego podejścia łączącego zaawansowane materiały, zoptymalizowaną geometrię i odpowiednie smarowanie. 🎯
Predykcyjne modelowanie tarcia
Matematyczne modele tarcia
Dokładne przewidywanie tarcia wymaga zaawansowanego modelowania:
- Tarcie kulombowskie: F = μ × N (model podstawowy)
- Krzywa Stribeck: Tarcie zmieniające się wraz z prędkością
- Wpływ temperatury: zależności μ(T)
- Progresja zużycia: Tarcie zmienia się w czasie
Wnioski
Zrozumienie podstawowej fizyki siłowników obrotowych typu łopatkowego - od dynamiki ciśnienia i termodynamiki po mechanizmy tarcia - umożliwia inżynierom optymalizację wydajności, przewidywanie zachowania i rozwiązywanie złożonych wyzwań związanych z aplikacjami.
Najczęściej zadawane pytania dotyczące fizyki siłowników obrotowych typu łopatkowego
P: W jaki sposób ciśnienie robocze wpływa na związek między teoretycznym a rzeczywistym momentem obrotowym?
O: Wyższe ciśnienie robocze generalnie poprawia teoretyczny stosunek momentu obrotowego do rzeczywistego, ponieważ straty mechaniczne stają się mniejszym procentem całkowitej mocy wyjściowej. Jednak zwiększone ciśnienie zwiększa również siły tarcia, więc zależność nie jest liniowa. Optymalne ciśnienie zależy od konkretnych wymagań aplikacji i konstrukcji siłownika.
P: Dlaczego siłowniki obrotowe tracą moment obrotowy przy dużych prędkościach i jak można to zminimalizować?
O: Utrata momentu obrotowego przy dużych prędkościach występuje z powodu zwiększonego tarcia, ograniczeń przepływu i efektów termodynamicznych. Zminimalizuj straty poprzez zoptymalizowany rozmiar portów, zaawansowane systemy łożysk, ulepszone projekty uszczelnień i zarządzanie termiczne. Ograniczenia prędkości przepływu stają się głównym ograniczeniem powyżej pewnych prędkości.
P: Jak zmiany temperatury wpływają na obliczenia wydajności siłownika obrotowego?
O: Temperatura wpływa na gęstość powietrza (wpływa na siłę), lepkość (wpływa na przepływ), właściwości materiału (zmienia tarcie) i rozszerzalność cieplną (zmienia luzy). Wzrost temperatury o 100°F może zmniejszyć wyjściowy moment obrotowy o 15-25% poprzez połączone efekty. Kompensacja temperatury w systemach sterowania pomaga utrzymać stałą wydajność.
P: Jaki jest związek między prędkością końcówki łopatki a stratami tarcia w siłownikach obrotowych?
O: Straty tarcia generalnie rosną wraz z kwadratem prędkości końcówki ze względu na zwiększone siły kontaktowe i wytwarzanie ciepła. Jednak przy bardzo niskich prędkościach dominuje tarcie statyczne, tworząc złożoną zależność. Optymalne prędkości robocze zazwyczaj mieszczą się w środkowym zakresie, gdzie tarcie dynamiczne jest możliwe do opanowania.
P: Jak uwzględnić efekt ściśliwości powietrza w obliczeniach wydajności siłownika obrotowego?
O: Ściśliwość powietrza staje się istotna przy ciśnieniu powyżej 100 PSI i podczas gwałtownego przyspieszania. Zamiast założeń o nieściśliwości należy stosować równania przepływu ściśliwego, uwzględniać opóźnienia propagacji fali ciśnienia i efekty rozprężania adiabatycznego. Rzeczywiste właściwości gazu mogą być potrzebne do zastosowań wysokociśnieniowych powyżej 200 PSI.
-
Poznaj definicję ramienia momentu, prostopadłej odległości od osi obrotu do linii działania siły, która ma kluczowe znaczenie dla obliczania momentu obrotowego. ↩
-
Zrozumienie zasady Pascala, podstawowego prawa mechaniki płynów, które wyjaśnia, w jaki sposób ciśnienie jest przenoszone w zamkniętym płynie. ↩
-
Poznaj dziedzinę obliczeniowej dynamiki płynów (CFD), gałęzi mechaniki płynów, która wykorzystuje analizę numeryczną do rozwiązywania i analizowania problemów związanych z przepływem płynów. ↩




