
Vă confruntați cu viteze inconsecvente ale cilindrilor pneumatici sau cu impacturi neașteptate la sfârșitul cursei? Aceste probleme frecvente provin adesea dintr-o înțelegere deficitară a cinematicii pistonului. Mulți ingineri se concentrează doar pe cerințele de forță, neglijând parametrii critici de mișcare care determină performanța sistemului.
Cinematica pistonului1 au un impact direct asupra performanței sistemelor pneumatice prin relațiile presiune-velocitate, limitele de accelerație și cerințele de amortizare. Înțelegerea acestor principii permite inginerilor să dimensioneze corect componentele, să prevadă profilurile de mișcare reale și să prevină defecțiunile premature ale cilindrilor fără tijă și ale altor actuatoare pneumatice.
În cei peste 15 ani petrecuți la Bepto lucrând cu sisteme pneumatice, am văzut nenumărate cazuri în care înțelegerea acestor principii fundamentale a ajutat clienții să rezolve probleme persistente de performanță și să prelungească durata de viață a echipamentelor de 3-5 ori.
Tabla de conținut
- De ce presiune aveți nevoie de fapt pentru o mișcare cu viteză constantă?
- Cum se calculează accelerația maximă posibilă în cilindrii pneumatici?
- De ce este important timpul de amortizare și cum se calculează acesta?
- Concluzie
- Întrebări frecvente despre cinematica pistonului în sistemele pneumatice
De ce presiune aveți nevoie de fapt pentru o mișcare cu viteză constantă?
Mulți ingineri aplică pur și simplu presiunea maximă disponibilă sistemelor lor pneumatice, dar această abordare este ineficientă și poate duce la mișcări sacadate, uzură excesivă și risipă de energie.
Presiunea necesară pentru o mișcare cu viteză constantă într-un cilindru pneumatic se calculează folosind P = (F + Fr)/A, unde P este presiunea, F este forța de încărcare externă, Fr este rezistența la frecare, iar A este suprafața pistonului. Acest calcul asigură o funcționare lină și eficientă, fără presiune excesivă care irosește energie și accelerează uzura componentelor.
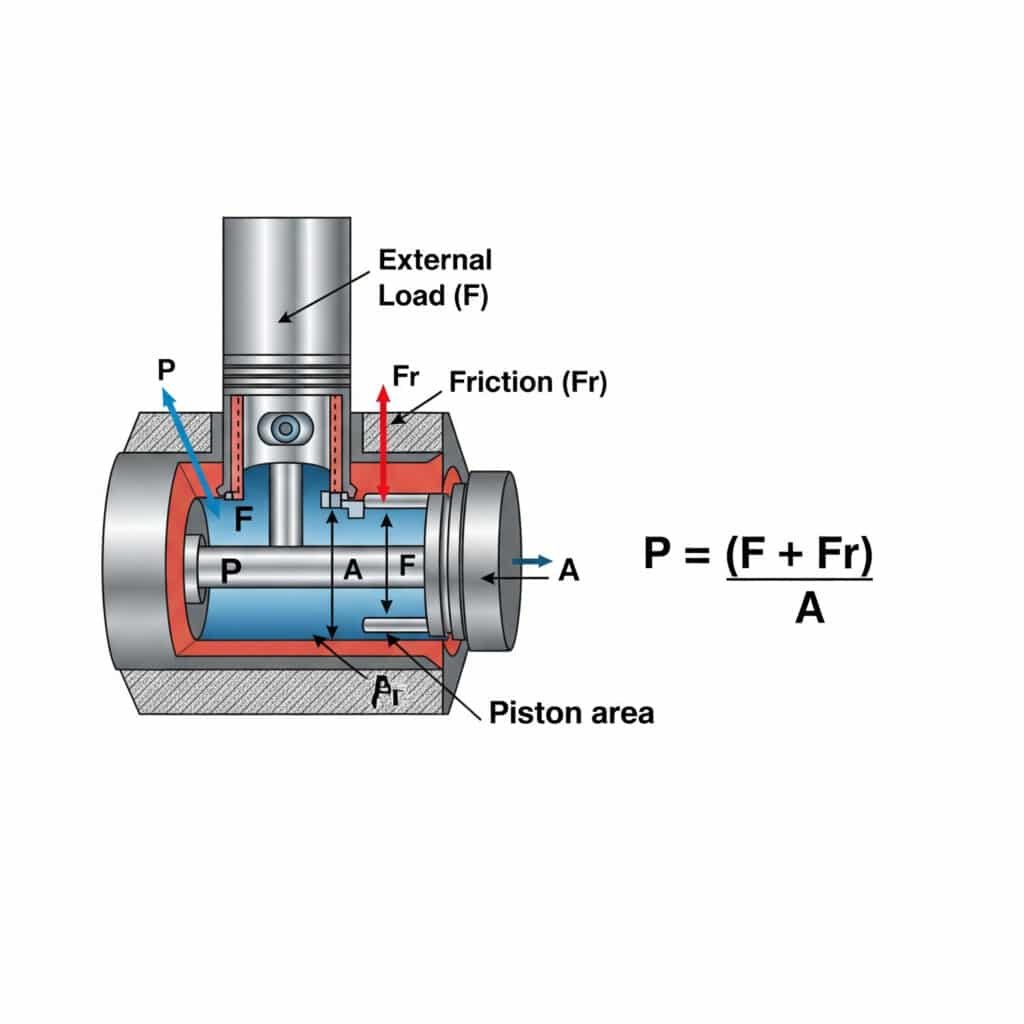
Înțelegerea cerințelor de presiune pentru mișcarea cu viteză constantă are implicații practice pentru proiectarea și funcționarea sistemului. Permiteți-mi să detaliez aceste aspecte în idei concrete.
Factori care afectează cerințele de presiune pentru viteză constantă
Presiunea necesară pentru menținerea vitezei constante depinde de mai mulți factori:
| Factor | Impactul asupra cerinței de presiune | Considerații practice |
|---|---|---|
| Sarcina externă | Relație liniară directă | Variază în funcție de orientare și de forțele externe |
| Fricțiune | Adaugă la presiunea necesară | Modificări cu uzura și lubrifierea garniturilor |
| Zona pistonului | Invers proporțional | Alezaj mai mare = cerințe de presiune mai mici |
| Restricții privind alimentarea cu aer | Căderi de presiune în conducte/valve | Dimensionarea componentelor pentru scăderea minimă a presiunii |
| Contrapresiune | Se opune moțiunii | Luați în considerare capacitatea debitului de evacuare |
Calcularea presiunii minime pentru o mișcare stabilă
Pentru a determina presiunea minimă necesară pentru o mișcare stabilă:
- Calculați forța necesară pentru a depăși sarcina externă
- Adăugați forța de frecare (de obicei 3-20% din forța maximă)
- Împărțiți la suprafața efectivă a pistonului
- Adăugați un factor de stabilitate (de obicei 10-30%)
De exemplu, într-un cilindru fără tijă cu alezaj de 40 mm, cu o sarcină de 10 kg și frecare 15%:
| Parametru | Calculul | Rezultat |
|---|---|---|
| Forța de încărcare | 10kg × 9,81m/s² | 98.1N |
| Forța de frecare | 15% de forță maximă la 6 bar | ~45N |
| Forța totală | 98,1N + 45N | 143.1N |
| Zona pistonului | π × (0,02m)² | 0.00126m² |
| Presiune minimă | 143.1N ÷ 0.00126m² | 113,571 Pa (1,14 bar) |
| Cu 20% Factor de stabilitate | 1,14 bar × 1,2 | 1,37 bar |
Aplicație din lumea reală: Economii de energie prin optimizarea presiunii
Anul trecut, am lucrat cu Robert, un inginer de producție la o fabrică de mobilă din Michigan. Linia sa automatizată de asamblare folosea cilindri fără tijă care funcționau la presiunea maximă de alimentare de 6 bari, indiferent de sarcină.
După analizarea aplicației sale, am stabilit că majoritatea mișcărilor necesită doar 2,5-3 bar pentru o funcționare stabilă. Prin instalarea regulatoare de presiune proporționale, am redus consumul de aer cu 40%, menținând în același timp durata ciclului. Acest lucru a economisit aproximativ $12.000 anual în costuri de energie, reducând în același timp uzura garniturilor și prelungind intervalele de întreținere.
Relația viteză-presiune în sistemele reale
În practică, relația dintre presiune și viteză nu este perfect liniară din cauza:
- Restricții de debit: Dimensionarea supapei și a orificiului afectează viteza maximă realizabilă
- Efectele compresibilității: Aerul este compresibil, cauzând întârzieri la accelerare
- Fenomene de lipire-derapare: Caracteristicile de frecare se modifică odată cu viteza
- Efecte inerțiale: Accelerarea masei necesită forță/presiune suplimentară
Cum se calculează accelerația maximă posibilă în cilindrii pneumatici?
Înțelegerea limitelor de accelerație este esențială pentru prevenirea șocurilor excesive, a vibrațiilor și a defecțiunilor premature ale componentelor în sistemele pneumatice.
Accelerația maximă posibilă într-un cilindru pneumatic se calculează folosind a = (P × A - F - Fr)/m, unde a este accelerația, P este presiunea, A este suprafața pistonului, F este sarcina externă, Fr este rezistența la frecare, iar m este masa în mișcare. Această ecuație definește limitele fizice ale vitezei cu care un actuator pneumatic poate porni sau opri mișcarea.
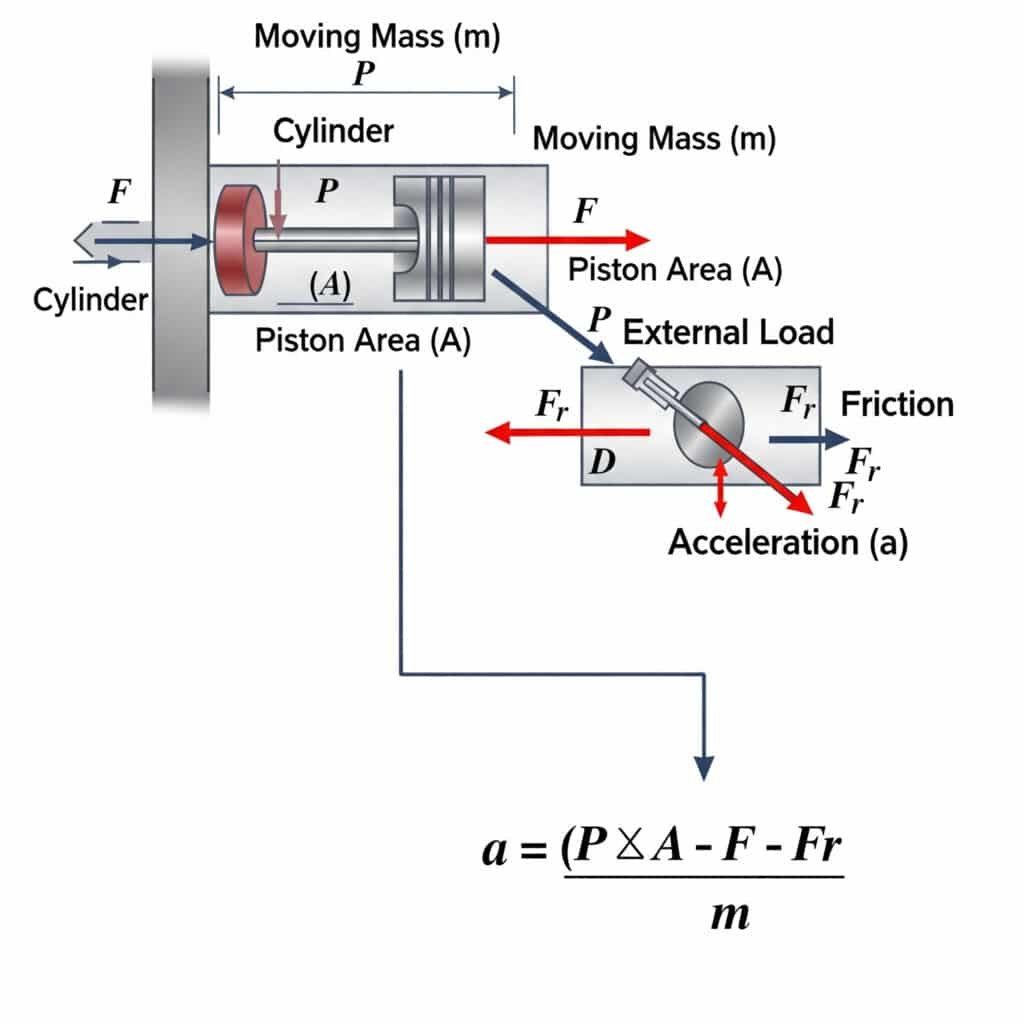
Limitele teoretice ale accelerației au implicații practice semnificative pentru proiectarea sistemului și selectarea componentelor.
Derivarea ecuației limită a accelerației
Ecuația limită a accelerației provine din A doua lege a lui Newton2 (F = ma):
- Forța netă disponibilă pentru accelerație este: Fnet = Fpresiune - Fîncărcare - Ffricțiune
- Fpresiune = P × A
- Prin urmare: a = Fnet/m = (P × A - F - Fr)/m
Limite practice de accelerație pentru diferite tipuri de cilindri
Diferitele modele de cilindri au diferite limite practice de accelerație:
| Tip cilindru | Accelerație maximă tipică | Factori limitativi |
|---|---|---|
| Cilindru cu tijă standard | 10-15 m/s² | Flambarea tijei, încărcări ale rulmenților |
| Cilindru fără tijă (magnetic) | 8-12 m/s² | Puterea de cuplare magnetică |
| Cilindru fără tijă (mecanic) | 15-25 m/s² | Designul garniturii/cozinetului, frecarea internă |
| Cilindru de ghidare | 20-30 m/s² | Rigiditatea sistemului de ghidare, capacitatea portantă |
| Cilindru de impact | 50-100+ m/s² | Proiectat special pentru accelerație ridicată |
Considerații privind masa în calculele de accelerație
La calcularea accelerației, este esențial să se includă toate masele în mișcare:
- Ansamblul pistonului: Include piston, garnituri și elemente de legătură
- Masa de încărcare: Sarcina externă care este deplasată
- Masa efectivă a aerului în mișcare: Adesea neglijabil, dar relevant în aplicațiile de mare viteză
- Masă adăugată datorită componentelor de montare: Suporturi, senzori, etc.
Odată am ajutat un client din Franța care se confrunta cu defecțiuni misterioase ale sistemului său de cilindri fără tijă. Cilindrul a fost dimensionat corect pentru sarcina declarată de 15 kg, dar ceda constant după câteva mii de cicluri.
După investigații, am descoperit că a omis să ia în considerare masa de 12 kg a plăcii de montare și a accesoriilor. Masa reală în mișcare a fost aproape dublă față de cea calculată de el, cauzând forțe de accelerație care depășeau limitele de proiectare ale cilindrului. După trecerea la un cilindru mai mare, defecțiunile au încetat complet.
Metode de control al accelerației
Pentru a controla accelerația în limite de siguranță:
- Supape de control al debitului: Limitarea debitului în timpul mișcării inițiale
- Supape proporționale: Asigurarea unei creșteri controlate a presiunii
- Accelerare în mai multe etape: Utilizați creșteri treptate ale presiunii
- Amortizarea mecanică: Adăugați amortizoare externe
- Control electronic: Utilizare sisteme servo-pneumatice3 cu reacție la accelerație
De ce este important timpul de amortizare și cum se calculează acesta?
Amortizarea adecvată la sfârșitul cursei este esențială pentru prevenirea deteriorării la impact, reducerea zgomotului și prelungirea duratei de viață a cilindrilor pneumatici. Înțelegerea timpului de amortizare ajută inginerii să proiecteze sisteme care echilibrează timpul de ciclu cu longevitatea componentelor.
Timpul de amortizare în cilindrii pneumatici este calculat folosind ecuația t = √(2s/a), unde t este timpul, s este lungimea cursei de amortizare, iar a este decelerația. Acest timp reprezintă timpul necesar pentru decelerarea în siguranță a masei în mișcare înainte de impact, ceea ce este esențial pentru prevenirea deteriorării cilindrului și a componentelor atașate.

Să explorăm aspectele practice ale calculării timpului de amortizare și implicațiile acestora pentru proiectarea sistemului.
Fizica din spatele amortizoarelor pneumatice
Amortizare pneumatică funcționează prin compresie controlată a aerului și evacuare restricționată:
- Pe măsură ce pistonul intră în camera de amortizare, calea de evacuare este restricționată
- Aerul blocat se comprimă, creând o contrapresiune în creștere
- Această contrapresiune creează o forță contrară care decelerază pistonul
- Profilul de decelerare depinde de designul și ajustarea pernei
Calcularea timpului optim de amortizare
Timpul optim de amortizare echilibrează prevenirea impactului cu eficiența timpului de ciclu:
| Parametru | Formula | Exemplu |
|---|---|---|
| Distanța de amortizare | Pe baza designului cilindrului | 15 mm (tipic pentru o gaură de 40 mm) |
| Decelerare necesară | a = v²/(2s) | Pentru v=0,5m/s, s=15mm: a = 8,33m/s² |
| Timp de amortizare | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Acumularea de presiune | P = P₀(V₀/V)^γ | Depinde de geometria camerei pernei |
Factorii care afectează performanța amortizării
Mai mulți factori influențează performanța reală de amortizare:
- Design cu etanșare cu pernă: Afectează scurgerile de aer în timpul amortizării
- Reglarea supapei acului: Controlează rata de restricționare a evacuării
- Masa în mișcare: Sarcinile mai grele necesită un timp de amortizare mai lung
- Viteza de apropiere: Vitezele mai mari necesită o distanță mai mare între perne
- Presiunea de funcționare: Afectează forța maximă de contracarare disponibilă
Tipuri de amortizoare și aplicațiile lor
Diferitele mecanisme de amortizare sunt adecvate pentru diferite aplicații:
| Tip amortizare | Caracteristici | Cele mai bune aplicații |
|---|---|---|
| Amortizare fixă | Simplu, nereglabil | Sarcini ușoare, funcționare constantă |
| Amortizare reglabilă | Reglabil cu supape cu ac | Sarcini variabile, aplicații flexibile |
| Amortizare autoreglabilă | Se adaptează la diferite condiții | Modificarea vitezelor și a încărcărilor |
| Amortizoare externe | Absorbție mare de energie | Sarcini grele, viteze mari |
| Amortizare electronică | Decelerare controlată cu precizie | Sisteme servo-pneumatice |
Studiu de caz: Optimizarea amortizării în aplicații cu ciclu de viață ridicat
Am lucrat recent cu Thomas, un inginer proiectant la un producător de componente auto din Germania. Linia sa de asamblare folosea cilindri fără tijă care funcționau la 45 de cicluri pe minut, dar se confrunta frecvent cu defecțiuni ale garniturilor și cu deteriorarea suportului de montare.
Analiza a arătat că timpul de amortizare a fost prea scurt pentru masa în mișcare, provocând forțe de impact de aproape 3G la fiecare capăt al cursei. Prin creșterea cursei de amortizare de la 12 mm la 20 mm și optimizarea setărilor valvei acului, am extins timpul de amortizare de la 0,04 s la 0,07 s.
Această schimbare aparent mică a redus forțele de impact cu peste 60%, a eliminat complet deteriorarea suportului și a prelungit durata de viață a garniturii de la 3 luni la peste un an - toate acestea menținând timpul de ciclu necesar.
Procedură practică de reglare a amortizorului
Pentru performanțe optime de amortizare în cilindrii fără tijă:
- Porniți cu supapele de amortizare complet deschise (restricție minimă)
- Închideți treptat supapa de amortizare până când se obține o decelerare lină
- Testare cu sarcini minime și maxime preconizate
- Verificarea performanțelor de amortizare pe întreaga gamă de viteze
- Ascultați sunetele de impact care indică o amortizare insuficientă
- Măsurați timpul real de decelerare pentru a confirma calculele
Concluzie
Înțelegerea principiilor cinematicii pistonului - de la cerințele de presiune pentru o viteză constantă până la limitele accelerației și calculele timpului de amortizare - este esențială pentru proiectarea unor sisteme pneumatice eficiente și fiabile. Prin aplicarea acestor principii la aplicațiile dumneavoastră cu cilindri fără tijă, puteți optimiza performanța, reduce consumul de energie și prelungi semnificativ durata de viață a componentelor.
Întrebări frecvente despre cinematica pistonului în sistemele pneumatice
De ce presiune am nevoie pentru o anumită turație a cilindrului?
Presiunea necesară depinde de sarcină, de frecare și de suprafața cilindrului. Calculați-o folosind P = (F + Fr)/A, unde F este forța de încărcare externă, Fr este rezistența la frecare, iar A este suprafața pistonului. Pentru un cilindru tipic fără tijă care deplasează orizontal o sarcină de 10 kg, veți avea nevoie de aproximativ 1,5-2 bar pentru o mișcare stabilă la viteze moderate.
Cât de repede poate accelera un cilindru pneumatic?
Accelerația maximă a unui cilindru pneumatic se calculează folosind a = (P × A - F - Fr)/m. Cilindrii tipici fără tijă pot atinge o accelerație de 10-25 m/s², în funcție de design. Aceasta se traduce prin atingerea unei viteze de 0,5 m/s în aproximativ 20-50 de milisecunde în condiții optime.
Ce factori limitează viteza maximă a unui cilindru fără tijă?
Viteza maximă este limitată de capacitatea de debit a supapei, volumul de alimentare cu aer, dimensiunea orificiului, capacitățile de amortizare și designul garniturii. Majoritatea cilindrilor standard fără tijă sunt proiectați pentru viteze maxime de 0,8-1,5 m/s, deși modelele specializate de mare viteză pot atinge 2-3 m/s.
Cum pot calcula amortizarea adecvată pentru aplicația mea?
Calculați amortizarea adecvată prin determinarea energiei cinetice (KE = ½mv²) a încărcăturii în mișcare și asigurându-vă că sistemul de amortizare poate absorbi această energie. Timpul de amortizare trebuie calculat folosind t = √(2s/a), unde s este distanța de amortizare și a este rata de decelerare dorită.
Ce se întâmplă dacă cilindrul meu pneumatic accelerează prea repede?
Accelerația excesivă poate cauza stres mecanic asupra componentelor de montare, uzura prematură a garniturilor, creșterea vibrațiilor și a zgomotului, posibila deplasare a sarcinii sau deteriorare și reducerea preciziei sistemului. De asemenea, poate duce la mișcări sacadate care afectează calitatea produselor în aplicații de precizie.
Cum afectează orientarea sarcinii presiunea necesară pentru mișcare?
Orientarea sarcinii are un impact semnificativ asupra cerințelor de presiune. Sarcinile verticale care se deplasează împotriva gravitației necesită o presiune suplimentară pentru a depăși forța gravitațională (P = F/A + Fg/A + Fr/A). Sarcinile orizontale trebuie să depășească doar frecarea și inerția. Sarcinile înclinate se încadrează între aceste extreme în funcție de sinusul unghiului.
-
Oferă o explicație fundamentală a cinematicii, ramura mecanicii care descrie mișcarea obiectelor fără a lua în considerare forțele care provoacă mișcarea.
semnal electronic de intrare, permițând controlul pneumatic avansat. ↩ -
Detalii A doua lege a lui Newton (F=ma), principiul fundamental al fizicii care pune în relație forța care acționează asupra unui obiect cu masa și accelerația acestuia, care este baza tuturor calculelor dinamice. ↩
-
Descrie servo-pneumatica, o tehnologie de control avansată care combină puterea pneumatică cu precizia controlului electronic în buclă închisă pentru a obține profiluri de poziționare și mișcare extrem de precise. ↩


