Vă confruntați cu viteze reduse ale cilindrilor, mișcări inconsecvente sau forță insuficientă în sistemele dvs. pneumatice? Aceste probleme comune provin adesea dintr-un vinovat neînțeles: rezistența la curgere. Mulți ingineri își dimensionează componentele pneumatice doar pe baza cerințelor de presiune și forță, trecând cu vederea impactul critic al rezistenței la curgere asupra performanței reale.
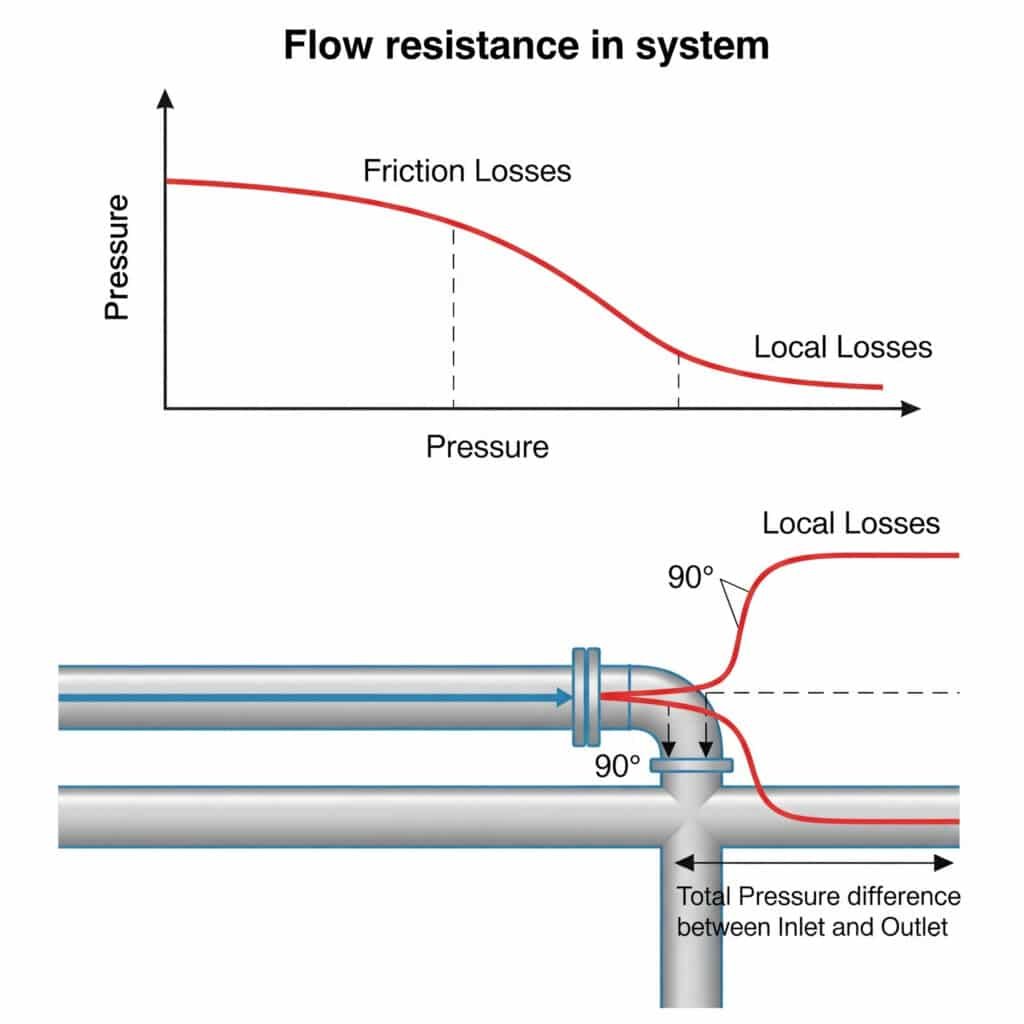
Rezistența la curgere în sistemele pneumatice creează căderi de presiune care reduc forța disponibilă, limitează viteza maximă și provoacă mișcări inconsecvente. Această rezistență provine atât din frecarea de-a lungul conductelor drepte (pierderi prin frecare), cât și din întreruperile la fitinguri, coturi și supape (pierderi locale). Împreună, aceste rezistențe pot reduce performanța reală a sistemului cu 20-50% comparativ cu calculele teoretice.
În cei peste 15 ani petrecuți la Bepto lucrând cu sisteme pneumatice, am văzut nenumărate cazuri în care înțelegerea și abordarea rezistenței la curgere au transformat sistemele neperformante în operațiuni fiabile și eficiente. Permiteți-mi să vă împărtășesc ceea ce am învățat despre calcularea și minimizarea acestor factori ascunși care ucid performanța.
Tabla de conținut
- Cum se calculează de fapt pierderile prin frecare în conductele pneumatice?
- De ce este esențială metoda lungimii echivalente pentru proiectarea precisă a sistemului?
- Ce se întâmplă când aerul circulă prin secțiuni cu alezaj redus?
- Concluzie
- Întrebări frecvente despre rezistența la curgere în sistemele pneumatice
Cum se calculează de fapt pierderile prin frecare în conductele pneumatice?
Pierderile prin frecare în țevi și tuburi drepte reprezintă baza calculelor de rezistență la curgere, însă mulți ingineri se bazează pe reguli empirice simplificate excesiv, care conduc la sisteme subdimensionate.
Pierderile prin frecare în conductele pneumatice sunt calculate folosind Ecuația Darcy-Weisbach1: ΔP = λ(L/D)(ρv²/2), unde λ este factorul de frecare, L este lungimea conductei, D este diametrul conductei, ρ este densitatea aerului, iar v este viteza de curgere. Pentru sistemele pneumatice, factorul de frecare λ variază în funcție de Numărul Reynolds2 și rugozitatea relativă, și se determină de obicei folosind tabele de căutare sau Diagrama Moody3.
Înțelegerea pierderilor prin frecare are implicații practice pentru proiectarea și depanarea sistemelor. Permiteți-mi să detaliez aceste aspecte în informații utile.
Utilizarea eficientă a tabelelor cu factori de frecare
Factorul de frecare (λ) este parametrul cheie în calcularea căderilor de presiune, dar determinarea valorii sale necesită luarea în considerare a condițiilor de curgere:
| Regimul de curgere | Numărul Reynolds (Re) | Determinarea factorului de frecare |
|---|---|---|
| Flux laminar | Re < 2000 | λ = 64/Re |
| Flux de tranziție | 2000 < Re < 4000 | Nefiabil - evitați proiectarea în acest interval |
| Curgere turbulentă | Re > 4000 | Utilizați tabele de căutare bazate pe rugozitatea relativă (ε/D) |
Tabel practic de căutare a factorului de frecare
Pentru curgerea turbulentă în sistemele pneumatice, utilizați acest tabel simplificat:
| Material țeavă | Rugozitatea relativă (ε/D) | Factor de frecare (λ) la numere comune de Reynolds |
|---|---|---|
| Re = 10,000 | ||
| Tuburi netede (PVC, poliuretan) | 0.0001 – 0.0005 | 0.031 |
| Tuburi din aluminiu | 0.001 – 0.002 | 0.035 |
| Oțel galvanizat | 0.003 – 0.005 | 0.042 |
| Oțel ruginit | 0.01 – 0.05 | 0.054 |
Calcularea căderii de presiune în sistemele pneumatice reale
Haideți să parcurgem un exemplu practic:
| Parametru | Valoare/Calcul | Exemplu |
|---|---|---|
| Diametrul conductei (D) | Diametru intern | 8mm (0.008m) |
| Lungimea conductei (L) | Lungimea totală dreaptă | 5m |
| Debit (Q) | De la cerințele de sistem | 20 litri/secundă standard |
| Densitatea aerului (ρ) | La presiunea de funcționare | 7,2 kg/m³ la 6 bar |
| Viteza debitului (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Numărul Reynolds (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1.273.600 |
| Rugozitatea relativă | Pentru tuburi din poliuretan | 0.0003 |
| Factor de frecare (λ) | Din tabelul de căutare | 0.017 |
| Cădere de presiune (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Aplicație din lumea reală: Rezolvarea problemelor legate de viteza cilindrilor
Anul trecut, am lucrat cu Sarah, un inginer de producție la o companie de echipamente de ambalare din Wisconsin. Sistemul ei de cilindri fără tijă funcționa la doar 60% din viteza așteptată, în ciuda faptului că avea un cilindru de dimensiuni corecte și o presiune de alimentare adecvată.
După ce i-am analizat sistemul, am descoperit că folosea tuburi de 6 mm pentru o aplicație cu debit mare. Pierderile prin frecare cauzau o cădere de presiune de 2,1 bar, reducând semnificativ forța și viteza disponibile. Prin trecerea la tuburi de 10 mm, am redus căderea de presiune la 0,4 bar, iar sistemul ei a atins imediat performanța necesară fără alte modificări.
Factorii care afectează pierderile prin frecare în sistemele reale
Mai mulți factori influențează pierderile reale prin frecare:
- Temperatura aerului: Temperaturile ridicate cresc vâscozitatea și frecarea
- Contaminare: Murdăria și uleiul pot crește rugozitatea efectivă
- Îndoirea tuburilor: Micro-deformarea în tuburile îndoite crește rezistența
- Deteriorarea vârstei: Coroziunea și depunerile cresc rugozitatea în timp
- Presiunea de funcționare: Presiunile mai mari cresc densitatea și pierderile
De ce este esențială metoda lungimii echivalente pentru proiectarea precisă a sistemului?
Pierderile locale la fitinguri, supape și coturi depășesc adesea pierderile prin frecare în conductele drepte, însă mulți ingineri fie le ignoră, fie folosesc metode de estimare grosolane care conduc la probleme de performanță.
Metoda lungimii echivalente convertește pierderile locale de la fitinguri și supape într-o lungime echivalentă de conductă dreaptă care ar cauza aceeași cădere de presiune. Aceasta se calculează folosind Le = K(D/λ), unde Le este lungimea echivalentă, K este coeficient de pierdere locală4, D este diametrul conductei, iar λ este factorul de frecare. Această metodă simplifică calculele și oferă previziuni mai precise privind performanța sistemului.
Să analizăm cum să aplicăm această metodă în mod eficient în proiectarea sistemelor pneumatice.
Tabele de lungimi echivalente pentru componente pneumatice comune
Iată un tabel de referință practic pentru componentele pneumatice comune:
| Componentă | Valoare K | Lungime echivalentă (Le/D) |
|---|---|---|
| Cot de 90° (ascuțit) | 0.9 | 30 |
| Cot de 90° (rază standard) | 0.3 | 10 |
| Cot de 45° | 0.2 | 7 |
| Joncțiunea T (debit de trecere) | 0.3 | 10 |
| T-Junction (flux ramificat) | 1.0 | 33 |
| Supapă cu bilă (complet deschisă) | 0.1 | 3 |
| Supapă cu poartă (complet deschisă) | 0.2 | 7 |
| Cupla cu conectare rapidă | 0.4-0.8 | 13-27 |
| Supapă de reținere | 1.5-2.5 | 50-83 |
| Supapă standard de control al debitului | 1.0-3.0 | 33-100 |
Aplicarea metodei lungimii echivalente
Pentru a utiliza această metodă în mod eficient:
- Identificați toate componentele din circuitul pneumatic
- Găsiți valoarea K sau raportul lungimii echivalente (Le/D) pentru fiecare componentă
- Calculați lungimea echivalentă prin înmulțirea cu diametrul conductei
- Adăugați toate lungimile echivalente la lungimea reală a țevii drepte
- Utilizați lungimea efectivă totală în calculele privind pierderile prin frecare
De exemplu, un sistem cu 5 m de tuburi drepte de 8 mm plus patru coturi de 90°, o îmbinare în T și două racorduri rapide:
| Componentă | Cantitate | Le/D | Lungime echivalentă |
|---|---|---|---|
| Coturi de 90° | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| T-Junction | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Conexiuni rapide | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Lungimea totală echivalentă | 0.72m | ||
| Lungime dreaptă reală | 5.00m | ||
| Lungimea totală efectivă | 5.72m |
Aceasta înseamnă că sistemul dvs. de 5 m se comportă de fapt ca un sistem de 5,72 m din cauza pierderilor locale - o creștere de 14,4% a lungimii efective.
Studiu de caz: Optimizarea amplasării supapei în sistemele de asamblare
L-am ajutat recent pe Miguel, un inginer de automatizări de la o fabrică de asamblare de electronice din Arizona. Sistemul său pick-and-place se confrunta cu mișcări inconsecvente și variații ale timpului de ciclu, în ciuda utilizării unor componente de înaltă calitate.
Analiza a arătat că colectorul de distribuție era situat la 3 m distanță de cilindri, iar circuitul includea numeroase fitinguri. Calculul lungimii echivalente a arătat că distanța reală de 3 m avea o lungime efectivă de 7,2 m din cauza pierderilor locale - mai mult decât dublu față de distanța pe țeavă dreaptă!
Prin relocarea colectorului de valve mai aproape de cilindri și eliminarea mai multor fitinguri, am redus lungimea efectivă de la 7,2 m la 2,1 m. Acest lucru a redus căderea de presiune cu 70%, rezultând o mișcare constantă și o reducere cu 15% a timpului de ciclu.
Sfaturi practice pentru minimizarea pierderilor locale
Pentru a reduce pierderile locale în sistemele dvs. pneumatice:
- Folosiți coate curbate sau rotunjite în loc de curbe ascuțite (reduce valoarea K cu 67%)
- Minimizarea numărului de fitinguri prin planificarea unei rute mai directe
- Selectați componente cu restricție redusă dacă este cazul, supape cu sferă cu orificiu complet
- Dimensiunea corectă a fitingurilor - racordurile subdimensionate cauzează pierderi disproporționate
- Plasați supapele aproape de actuatoare pentru a minimiza lungimea efectivă a tubului
Ce se întâmplă când aerul circulă prin secțiuni cu alezaj redus?
Secțiunile cu alezaj redus în circuitele pneumatice - cum ar fi supapele parțial închise, fitingurile subdimensionate sau tranzițiile de diametru - creează restricții semnificative de debit care pot afecta grav performanța sistemului.
Când aerul curge prin secțiuni cu alezaj redus, căderi de presiune5 apar conform formulei ΔP = ρ(v₂² - v₁²)/2, unde v₁ este viteza înainte de restricție și v₂ este viteza în restricție. Acest lucru poate fi compensat utilizând factorul de compensare a raportului de alezaj C = (1 - (d/D)⁴), unde d este diametrul redus și D este diametrul inițial. Acest factor ajută la predicția performanței reale a sistemului și la evitarea subdimensionării componentelor.
Să explorăm implicațiile practice ale secțiunilor de alezaj reduse și cum să le luăm în considerare în proiectarea sistemului.
Calcularea picăturilor de presiune la tranzițiile de diametru
Atunci când aerul curge de la un diametru mai mare la unul mai mic, căderea de presiune poate fi calculată folosind:
| Parametru | Formula | Exemplu |
|---|---|---|
| Diametrul original (D) | Din specificații | 10mm |
| Diametru redus (d) | Din specificații | 6mm |
| Raport alzaj (d/D) | Diviziune simplă | 0.6 |
| Debit (Q) | De la cerințele de sistem | 15 litri/secundă standard |
| Viteza în conducta originală (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Viteza în secțiunea redusă (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Cădere de presiune (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Factor de compensare (C) | C = (1 - (d/D)⁴) | 0.87 |
Scenarii comune de reducere a alezajului și impactul acestora
Iată cum afectează diferitele reduceri ale găurii capacitatea de debit:
| Reducerea alezajului | Reducerea capacității de debit | Creșterea căderii de presiune |
|---|---|---|
| 10mm la 8mm | 36% | 2.4× |
| 10mm la 6mm | 64% | 7.7× |
| 10mm la 4mm | 84% | 39× |
| 8mm la 6mm | 44% | 3.2× |
| 8mm la 4mm | 75% | 16× |
| 6mm la 4mm | 56% | 5.1× |
Aceste cifre evidențiază de ce reduceri aparent minore ale diametrului pot avea efecte dramatice asupra performanței sistemului.
Efectul cumulativ al restricțiilor multiple
În circuitele pneumatice reale, apar mai multe restricții în serie. Efectul lor este cumulativ și poate fi calculat folosind:
- Conversia fiecărei restricții în factorul C echivalent
- Calculați factorul C total: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Utilizați acest factor total pentru a determina reducerea globală a performanței sistemului
Studiu de caz: Rezolvarea problemelor de nepotrivire între valvă și actuator
Luna trecută, am lucrat cu Thomas, un supervizor de întreținere la o fabrică de mobilă din Carolina de Nord. Noul său sistem de cilindri fără tijă funcționa la mai puțin de jumătate din viteza așteptată, în ciuda utilizării dimensiunii recomandate de producător pentru valvă.
Ancheta a scos la iveală multiple reduceri de foraje în circuitul său:
- Conductă de alimentare de 10 mm la orificii de supapă de 8 mm (C₁ = 0,36)
- Orificii de supapă de 8 mm la fitinguri de 6 mm (C₂ = 0,44)
- Racorduri de 6 mm la orificii de cilindru de 8 mm cu restricții interne (C₃ = 0,32)
Factorul total de compensare a fost Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, ceea ce înseamnă că sistemul său pierdea 75% din capacitatea sa teoretică de debit!
Prin modernizarea cu componente dimensionate corespunzător în întregul sistem, am eliminat aceste restricții și am obținut performanța necesară fără a schimba cilindrul sau presiunea de alimentare.
Strategii practice de minimizare a pierderilor prin reducerea forajului
Pentru a reduce pierderile cauzate de reducerea forajului:
- Dimensiunea componentelor este consecventă în întregul circuit pneumatic
- Utilizați cea mai mare dimensiune practică a tubului pentru aplicații cu debit mare
- Acordați atenție restricțiilor privind componentele interne, nu doar dimensiunile conexiunilor
- Luați în considerare căile de curgere paralele pentru cerințe de debit mare
- Eliminați adaptoarele și tranzițiile inutile ori de câte ori este posibil
Principiul "verigii celei mai slabe" în sistemele pneumatice
Amintiți-vă că performanța sistemului dvs. pneumatic este limitată de componenta cea mai restrictivă a acestuia. Un singur element subdimensionat poate anula beneficiile componentelor dimensionate corespunzător din alte părți ale sistemului.
De exemplu, un sistem cu tuburi de 10 mm, supape de 10 mm, dar fitinguri de 6 mm la cilindru va funcționa în esență la fel ca un sistem cu componente de 6 mm pe toată lungimea - la un cost mai mare.
Concluzie
Înțelegerea și calcularea corectă a rezistenței la curgere - prin tabele de factori de frecare, metode de lungime echivalentă și compensarea găurii reduse - este esențială pentru proiectarea sistemelor pneumatice care funcționează conform așteptărilor în condiții reale. Aplicând aceste metode de calcul și principii de proiectare, puteți optimiza aplicațiile cilindrilor fără tijă și alte sisteme pneumatice pentru performanțe și fiabilitate maxime.
Întrebări frecvente despre rezistența la curgere în sistemele pneumatice
Câtă pierdere de presiune este acceptabilă într-un sistem pneumatic?
Căderea de presiune acceptabilă depinde de cerințele aplicației dvs., dar, ca orientare generală, limitați căderea de presiune totală la 10-15% din presiunea de alimentare pentru o funcționare eficientă. Pentru un sistem de 6 bar, aceasta înseamnă menținerea căderii totale de presiune sub 0,6-0,9 bar. Aplicațiile critice pot necesita căderi de presiune chiar mai mici, de 5-8%, pentru a menține performanțele constante.
Care este relația dintre diametrul tubului și căderea de presiune?
Căderea de presiune este invers proporțională cu puterea a cincea a diametrului (D⁵) pentru curgerea turbulentă în sistemele pneumatice. Aceasta înseamnă că dublarea diametrului tubului reduce căderea de presiune de aproximativ 32 de ori. De exemplu, creșterea tubului de la 6 mm la 12 mm poate reduce căderea de presiune de la 1,5 bar la doar 0,047 bar în aceleași condiții de curgere.
Cum determin dimensiunea corectă a tubului pentru aplicația mea pneumatică?
Selectați dimensiunea tubului în funcție de cerințele privind debitul și căderea de presiune acceptabilă. Calculați numărul Reynolds și factorul de frecare, apoi utilizați ecuația Darcy-Weisbach pentru a determina căderea de presiune pentru diferite diametre. Alegeți cel mai mic diametru care menține căderea de presiune în limite acceptabile (de obicei <10% din presiunea de alimentare), luând în considerare în același timp constrângerile de spațiu și costul.
Ce creează mai multă restricție: un cot de 90° sau 5 metri de tub drept?
Un cot ascuțit de 90° creează de obicei o rezistență echivalentă cu 30 de diametre de țeavă de tub drept. Pentru o țeavă de 8 mm, un cot ascuțit echivalează cu aproximativ 240 mm (30 × 8 mm) de țeavă dreaptă. Aceasta înseamnă că 5 metri de tuburi drepte creează o restricție de aproximativ 21 de ori mai mare decât un singur cot. Cu toate acestea, sistemele conțin adesea mai multe coturi și fitinguri, al căror efect cumulat poate depăși pierderile pe lungime dreaptă.
Cum afectează fitingurile cu conectare rapidă performanța sistemului?
Fitingurile standard cu conectare rapidă introduc, de obicei, o pierdere locală echivalentă cu 15-25 de diametre de țeavă de tub drept. Mai semnificativ, multe racorduri rapide au restricții interne mai mici decât dimensiunea lor nominală. Un racord rapid de "10 mm" poate avea o restricție internă de numai 7-8 mm, creând o reducere a găurii care poate reduce capacitatea de debit cu 50-70% în acel punct.
Care este impactul supapelor de control al debitului parțial închise asupra performanței sistemului?
O supapă de reglare a debitului închisă la 50% din suprafața sa totală nu reduce debitul cu doar 50% - reduce debitul cu aproximativ 75% datorită relației neliniare dintre diametru și capacitatea de debit. Pierderea de presiune crește în funcție de pătratul variației vitezei, astfel încât înjumătățirea diametrului efectiv crește pierderea de presiune de aproximativ 16 ori în aceleași condiții de debit.
-
Oferă o analiză detaliată a ecuației Darcy-Weisbach, o formulă fundamentală și utilizată pe scară largă în dinamica fluidelor pentru calcularea pierderilor de presiune datorate frecării într-o conductă. ↩
-
Oferă o definiție clară a numărului Reynolds, o mărime critică adimensională utilizată pentru a prezice tiparele de curgere (laminară sau turbulentă) în diferite situații de curgere a fluidelor. ↩
-
Prezintă diagrama Moody, un grafic cuprinzător care trasează factorul de frecare Darcy în funcție de numărul Reynolds și rugozitatea relativă, care este instrumentul standard pentru ingineri pentru a determina căderea de presiune în conducte. ↩
-
Explică conceptul de valoare K sau coeficient de pierdere locală, un număr adimensional utilizat pentru a caracteriza pierderea de presiune într-un racord de țeavă sau supapă ca parte a metodei lungimii echivalente. ↩
-
Detaliază fizica care stă la baza scăderii de presiune care apare atunci când un fluid trece printr-o restricție (un orificiu), pe baza principiilor ecuației continuității și a principiului lui Bernoulli. ↩



