
Vă străduiți să preziceți performanța reală a cilindrului pneumatic? Mulți ingineri calculează greșit forțele de ieșire și cerințele de presiune, ceea ce duce la defecțiuni ale sistemului și timpi morți costisitori. Dar există o modalitate simplă de a stăpâni aceste calcule.
Cilindrii pneumatici funcționează în conformitate cu principiile fizice fundamentale, în principal Legea lui Pascal1, care afirmă că presiunea aplicată unui fluid închis este transmisă în mod egal în toate direcțiile. Acest lucru ne permite să calculăm forța cilindrului prin înmulțirea presiunii cu suprafața efectivă a pistonului, debitele și unitățile de presiune necesitând conversii precise pentru proiectarea exactă a sistemului.
Am petrecut peste un deceniu ajutând clienții să-și optimizeze sistemele pneumatice și am văzut cum înțelegerea acestor principii de bază poate transforma fiabilitatea sistemului. Permiteți-mi să vă împărtășesc cunoștințele practice care vă vor ajuta să evitați greșelile comune pe care le văd în fiecare zi.
Tabla de conținut
- Cum determină legea lui Pascal randamentul forței cilindrului?
- Care este relația dintre debitul de aer și presiunea în cilindri?
- De ce este esențială înțelegerea conversiei unităților de presiune pentru proiectarea sistemului?
- Concluzie
- Întrebări frecvente despre fizica în sistemele pneumatice
Cum determină legea lui Pascal randamentul forței cilindrului?
Înțelegerea Legii lui Pascal este fundamentală pentru prezicerea și optimizarea performanței cilindrilor în orice sistem pneumatic.
Legea lui Pascal afirmă că presiunea exercitată asupra unui fluid într-un sistem închis este transmisă în mod egal în tot fluidul. Pentru cilindrii pneumatici, aceasta înseamnă că forța de ieșire este egală cu presiunea înmulțită cu aria efectivă a pistonului (F = P × A). Această relație simplă este baza pentru toate calculele forței cilindrului.

Derivarea calculului forței
Să analizăm derivarea matematică a calculelor forței cilindrice:
Ecuația de bază a forței
Ecuația fundamentală pentru forța cilindrică este:
F = P × A
Unde:
- F = Forța de ieșire (N)
- P = presiune (Pa)
- A = Suprafața efectivă a pistonului (m²)
Considerații privind zona efectivă
Zona efectivă diferă în funcție de tipul cilindrului și de direcție:
| Tip cilindru | Forța de extindere | Forța de retragere |
|---|---|---|
| Cu acțiune unică | P × A | Numai forța arcului |
| Cu dublu efect (standard) | P × A | P × (A - a) |
| Cu dublu efect (fără tijă) | P × A | P × A |
Unde:
- A = Suprafața totală a pistonului
- a = aria secțiunii transversale a tijei
M-am consultat odată cu o fabrică din Ohio care se confrunta cu o forță insuficientă în aplicația de presare. Calculele lor păreau corecte pe hârtie, dar performanța reală era slabă. În urma investigației, am descoperit că foloseau presiune manometrică2 în calculele lor, în loc de presiunea absolută, și nu au luat în considerare suprafața tijei în timpul retragerii. După recalcularea cu formula și valorile de presiune corecte, am reușit să dimensionăm corect sistemul lor, crescând productivitatea cu 23%.
Exemple practice de calcul al forței
Să examinăm câteva calcule din lumea reală:
Exemplul 1: Forța de extensie într-un cilindru standard
Pentru un cilindru cu:
- Diametrul alezajului = 50 mm (rază = 25 mm = 0,025 m)
- Presiune de funcționare = 6 bar (600.000 Pa)
Zona pistonului este:
A = π × r² = π × (0,025)² = 0,001963 m²
Forța de extensie este:
F = P × A = 600.000 Pa × 0,001963 m² = 1.178 N ≈ 118 kg forță
Exemplul 2: Forța de retragere în același cilindru
Dacă diametrul tijei este de 20 mm (rază = 10 mm = 0,01 m):
Zona tijei este:
a = π × r² = π × (0,01)² = 0,000314 m²
Zona de retracție efectivă este:
A - a = 0,001963 - 0,000314 = 0,001649 m²
Forța de retragere este:
F = P × (A - a) = 600.000 Pa × 0,001649 m² = 989 N ≈ 99 kg forță
Factori de eficiență în aplicații din lumea reală
În aplicațiile practice, mai mulți factori afectează calculul teoretic al forței:
Pierderi prin frecare
Frecarea dintre garnitura pistonului și peretele cilindrului reduce forța efectivă:
| Tip de garnitură | Factor de eficiență tipic |
|---|---|
| Standard NBR | 0.85-0.90 |
| PTFE cu frecare redusă | 0.90-0.95 |
| Etanșări îmbătrânite/uzate | 0.70-0.85 |
Ecuația practică a forței
O ecuație mai exactă a forței în lumea reală este:
F_actual = η × P × A
Unde:
- η (eta) = Factor de eficiență (de obicei 0,85-0,95)
Care este relația dintre debitul de aer și presiunea în cilindri?
Înțelegerea relației dintre debit și presiune este esențială pentru dimensionarea sistemelor de alimentare cu aer și prezicerea vitezei cilindrilor.
Debitul și presiunea aerului în sistemele pneumatice sunt invers legate - pe măsură ce presiunea crește, debitul scade de obicei. Această relație urmează legile gazelor și este afectată de restricții, temperatură și volumul sistemului. Funcționarea corectă a cilindrului necesită echilibrarea acestor factori pentru a obține viteza și forța dorite.
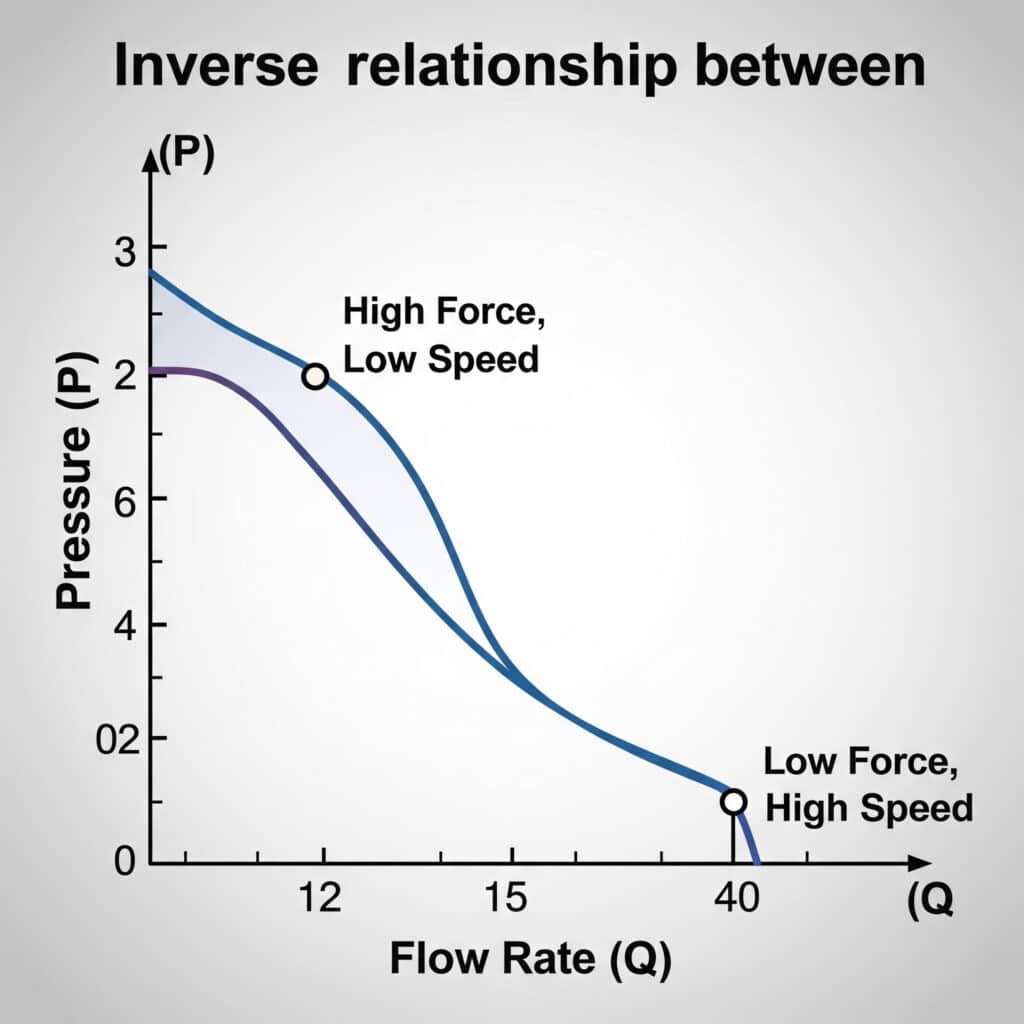
Tabelul de conversie debit-presiune
Acest tabel de referință practic arată relația dintre debit și căderea de presiune în diferite componente ale sistemului:
| Dimensiunea țevii (mm) | Debit (l/min) | Cădere de presiune (bar/metru) la o alimentare de 6 bar |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
Matematica debitului și a presiunii
Relația dintre debit și presiune urmează mai multe legi ale gazelor:
Ecuația lui Poiseuille3 pentru curgere laminară
Pentru fluxul laminar prin conducte:
Q = (π × r⁴ × ΔP) / (8 × η × L)
Unde:
- Q = debit volumetric
- r = raza conductei
- ΔP = Diferența de presiune
- η = Vâscozitatea dinamică
- L = Lungimea conductei
Coeficientul de curgere (Cv)4 Metoda
Pentru componente precum supapele:
Q = Cv × √ΔP
Unde:
- Q = debit
- Cv = Coeficient de debit
- ΔP = căderea de presiune prin componentă
Calcularea vitezei cilindrului
Viteza unui cilindru pneumatic depinde de debitul și de suprafața cilindrului:
v = Q / A
Unde:
- v = viteza cilindrului (m/s)
- Q = debit (m³/s)
- A = Suprafața pistonului (m²)
În timpul unui proiect recent la o instalație de ambalare din Franța, am întâlnit o situație în care cilindrii fără tijă ai clientului se mișcau prea încet, în ciuda unei presiuni adecvate. Analizând sistemul lor cu ajutorul calculelor noastre debit-presiune, am identificat linii de alimentare subdimensionate care provocau scăderi semnificative de presiune. După trecerea de la tuburi de 6 mm la tuburi de 10 mm, durata ciclului s-a îmbunătățit cu 40%, crescând dramatic capacitatea de producție.
Considerații critice privind fluxul
Mai mulți factori afectează relația debit-presiune în sistemele pneumatice:
Fenomenul fluxului înecat5
Atunci când raportul de presiune depășește o valoare critică (aproximativ 0,53 pentru aer), debitul devine "sufocat" și nu poate crește indiferent de reducerea presiunii din aval.
Efectele temperaturii
Debitul este influențat de temperatură conform relației:
Q₂ = Q₁ × √(T₂/T₁)
Unde:
- Q₁, Q₂ = debite la diferite temperaturi
- T₁, T₂ = Temperaturi absolute
De ce este esențială înțelegerea conversiei unităților de presiune pentru proiectarea sistemului?
Navigarea printre diferitele unități de presiune utilizate la nivel mondial este esențială pentru proiectarea corectă a sistemului și compatibilitatea internațională.
Conversia unităților de presiune este esențială deoarece componentele și specificațiile pneumatice utilizează unități diferite în funcție de regiune și industrie. Interpretarea greșită a unităților poate duce la erori de calcul semnificative, cu consecințe potențial periculoase. Conversia între presiunea absolută, manometrică și diferențială adaugă un alt nivel de complexitate.
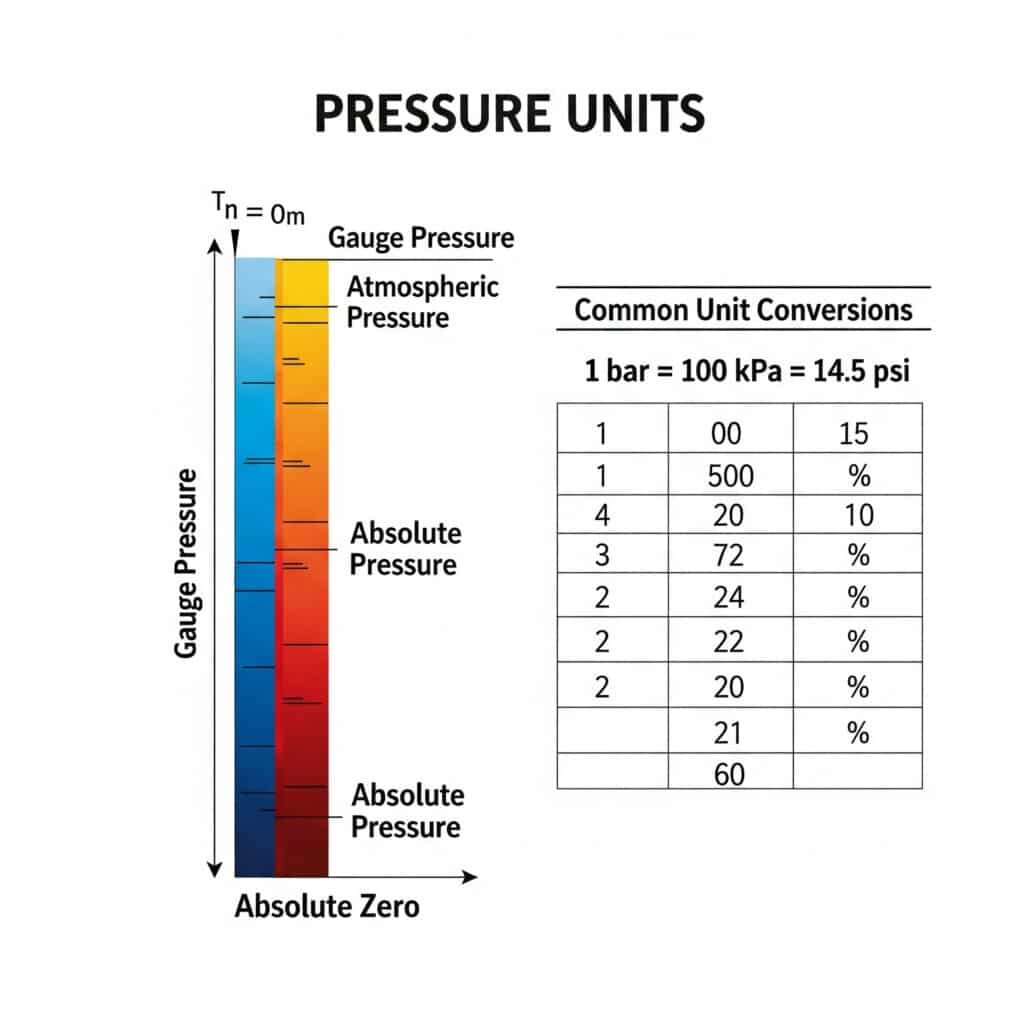
Ghid de conversie a unității de presiune absolută
Acest tabel de conversie cuprinzător ajută la navigarea prin diferitele unități de presiune utilizate la nivel global:
| Unitate | Simbol | Echivalent în Pa | Echivalent în bar | Echivalent în psi |
|---|---|---|---|---|
| Pascal | Pa | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| Bar | bar | 1 × 10⁵ | 1 | 14.5038 |
| Liră pe centimetru pătrat | psi | 6,894.76 | 0.0689476 | 1 |
| Kilogram-forță pe cm pătrat | kgf/cm² | 98,066.5 | 0.980665 | 14.2233 |
| Megapascal | MPa | 1 × 10⁶ | 10 | 145.038 |
| Atmosferă | atm | 101,325 | 1.01325 | 14.6959 |
| Torr | Torr | 133.322 | 0.00133322 | 0.0193368 |
| Milimetru de mercur | mmHg | 133.322 | 0.00133322 | 0.0193368 |
| Inch de apă | înH₂O | 249.089 | 0.00249089 | 0.0361274 |
Presiune absolută vs. presiune manometrică
Înțelegerea diferenței dintre presiunea absolută și presiunea manometrică este fundamentală:
Calculator de conversie a presiunii
Convertor unitate de presiune
Convertor debit cilindru
Formule de conversie
- P_absolute = P_gauge + P_atmospheric
- P_gauge = P_absolut - P_atmosferic
În cazul în care presiunea atmosferică standard este de aproximativ:
- 1,01325 bar
- 14.7 psi
- 101,325 Pa
Am lucrat odată cu o echipă de ingineri din Germania care achiziționase cilindrii noștri fără tijă, dar care a raportat că nu obțineau forța așteptată. După unele probleme, am descoperit că foloseau diagramele noastre de forță (care se bazau pe presiunea manometrică), dar introduceau valorile presiunii absolute. Această simplă neînțelegere cauza o eroare de calcul de 1 bar în așteptările lor privind forța. După clarificarea referinței de presiune, sistemul lor a funcționat exact conform specificațiilor.
Exemple practice de conversie
Să trecem în revistă câteva scenarii comune de conversie:
Exemplul 1: Conversia presiunii de lucru între unități
Un cilindru proiectat pentru o presiune maximă de lucru de 0,7 MPa:
În bar:
0,7 MPa × 10 bar/MPa = 7 bar
În psi:
0,7 MPa × 145,038 psi/MPa = 101,5 psi
Exemplul 2: Conversia de la presiune manometrică la presiune absolută
Un sistem care funcționează la o presiune manometrică de 6 bar:
În presiune absolută (bar):
6 bar_gauge + 1.01325 bar_atmospheric = 7.01325 bar_absolute
Exemplul 3: Conversia de la kgf/cm² la MPa
Un cilindru japonez specificat pentru 7 kgf/cm²:
În MPa:
7 kgf/cm² × 0,0980665 MPa/(kgf/cm²) = 0,686 MPa
Preferințele regionale ale unităților de presiune
Diferitele regiuni utilizează de obicei unități de presiune diferite:
| Regiunea | Unități de presiune comune |
|---|---|
| America de Nord | psi, inHg, inH₂O |
| Europa | bar, Pa, mbar |
| Japonia | kgf/cm², MPa |
| China | MPa, bar |
| MAREA BRITANIE | bar, psi, Pa |
Măsurarea presiunii în documentație
Atunci când documentați specificațiile de presiune, este esențial să indicați în mod clar:
- Valoarea numerică
- Unitatea de măsură
- Indiferent dacă este vorba de presiune manometrică (g) sau absolută (a)
De exemplu:
- 6 bar_g (presiune manometrică, 6 bar deasupra presiunii atmosferice)
- 7,01 bar_a (presiune absolută, presiune totală, inclusiv presiunea atmosferică)
Concluzie
Înțelegerea fizicii din spatele cilindrilor pneumatici - de la calculele forței conform Legii lui Pascal la relațiile debit-presiune și conversiile unităților de presiune - este esențială pentru proiectarea și depanarea corectă a sistemului. Aceste principii fundamentale vă ajută să vă asigurați că sistemele pneumatice oferă performanțele așteptate în mod fiabil și eficient.
Întrebări frecvente despre fizica în sistemele pneumatice
Cum pot calcula forța de ieșire a unui cilindru pneumatic fără tijă?
Pentru a calcula forța de ieșire a unui cilindru pneumatic fără tijă, înmulțiți presiunea de funcționare cu suprafața efectivă a pistonului (F = P × A). De exemplu, un cilindru fără tijă cu un orificiu de 50 mm (suprafață de 0,001963 m²) care funcționează la 6 bar (600.000 Pa) va produce o forță de aproximativ 1.178 N. Spre deosebire de cilindrii tradiționali, cilindrii fără tijă au de obicei aceeași suprafață efectivă în ambele direcții.
Cum pot calcula forța de ieșire a unui cilindru pneumatic fără tijă?
Pentru a calcula forța de ieșire a unui cilindru pneumatic fără tijă, înmulțiți presiunea de funcționare cu suprafața efectivă a pistonului (F = P × A). De exemplu, un cilindru fără tijă cu un orificiu de 50 mm (suprafață de 0,001963 m²) care funcționează la 6 bar (600.000 Pa) va produce o forță de aproximativ 1.178 N. Spre deosebire de cilindrii tradiționali, cilindrii fără tijă au de obicei aceeași suprafață efectivă în ambele direcții.
Care este diferența dintre presiunea manometrică și presiunea absolută?
Presiunea manometrică (bar_g, psi_g) măsoară presiunea în raport cu presiunea atmosferică, presiunea atmosferică fiind zero. Presiunea absolută (bar_a, psi_a) măsoară presiunea relativ la un vid perfect, care este zero. Pentru a trece de la presiunea manometrică la presiunea absolută, adăugați presiunea atmosferică (aproximativ 1,01325 bar sau 14,7 psi) la citirea manometrică.
Cum afectează fluxul de aer viteza cilindrilor?
Viteza cilindrului este direct proporțională cu debitul de aer și invers proporțională cu suprafața pistonului (v = Q/A). Debitul insuficient datorat conductelor de alimentare subdimensionate, fitingurilor restrictive sau supapelor inadecvate va limita viteza cilindrului indiferent de presiune. De exemplu, un debit de 20 litri/secundă printr-un cilindru cu o suprafață a pistonului de 0,002 m² va produce o viteză de 10 metri/secundă.
De ce cilindrii pneumatici se mișcă uneori mai lent decât se calculează?
Cilindrii pneumatici se pot mișca mai lent decât s-a calculat din cauza mai multor factori: restricțiile de alimentare cu aer care cauzează căderi de presiune, frecarea internă a garniturilor, sarcinile mecanice care depășesc calculele, scurgerile care reduc presiunea efectivă sau efectele temperaturii asupra densității aerului. În plus, coeficienții de debit ai supapelor limitează adesea debitul real disponibil pentru cilindru.
Cum convertesc între diferite unități de presiune pentru specificații internaționale?
Pentru a converti între unitățile de presiune, utilizați factorii de multiplicare: 1 bar = 100.000 Pa = 0,1 MPa = 14,5038 psi = 1,01972 kgf/cm². Verificați întotdeauna dacă presiunea este specificată ca manometrică sau absolută, deoarece această distincție poate afecta semnificativ calculele. De exemplu, 6 bar_g echivalează cu 7,01325 bar_a în condiții atmosferice standard.
Care este relația dintre dimensiunea alezajului cilindrului și forța de ieșire?
Relația dintre dimensiunea orificiului cilindrului și forța exercitată este pătratică - dublarea diametrului orificiului crește de patru ori forța exercitată (deoarece aria = π × r²). De exemplu, la o presiune de funcționare de 6 bar, un cilindru cu diametrul de 40 mm produce aproximativ 754 N de forță, în timp ce un cilindru cu diametrul de 80 mm produce aproximativ 3 016 N, de aproape patru ori mai mult.
-
Oferă o explicație detaliată a Legii lui Pascal, un principiu fundamental în mecanica fluidelor, care stă la baza transmiterii hidraulice și pneumatice a puterii. ↩
-
Oferă o definiție clară și o comparație între presiunea manometrică și presiunea absolută, o distincție esențială pentru calcule inginerești exacte, deoarece presiunea manometrică este relativă la presiunea atmosferică. ↩
-
Explică derivarea și aplicarea legii lui Poiseuille, care descrie căderea de presiune a unui fluid incompresibil și newtonian care curge printr-o conductă cilindrică lungă în regim laminar. ↩
-
Oferă o definiție tehnică a coeficientului de debit (Cv), o măsură imperială care oferă o modalitate standardizată de a compara capacitățile de debit ale diferitelor supape. ↩
-
Detaliază fizica debitului înecat, o condiție a dinamicii fluidelor care limitează debitul masic al unui fluid compresibil printr-o restricție atunci când viteza atinge viteza sunetului. ↩


