
Ați atins vreodată un cilindru pneumatic după o funcționare continuă și ați fost surprins de cât de cald se simte? Căldura nu este doar un inconvenient - reprezintă energie irosită, eficiență redusă și potențiale probleme de fiabilitate care ar putea să vă coste mii de euro.
Transferul de căldură în sistemele pneumatice are loc prin trei mecanisme: conducție prin materialele componentelor, convecție între suprafețe și aer și radiație de la suprafețele fierbinți. Înțelegerea și optimizarea acestor principii pot reduce temperaturile de funcționare cu 15-30%, pot prelungi durata de viață a componentelor cu până la 40% și pot îmbunătăți eficiența energetică cu 5-15%.
Luna trecută, am fost consultant pentru o fabrică de prelucrare a alimentelor din Georgia, unde cilindrii fără tijă cedau la fiecare 3-4 luni din cauza problemelor termice. Echipa lor de întreținere înlocuia pur și simplu componentele fără a aborda cauza principală. Prin aplicarea principiilor adecvate de transfer termic, am redus temperaturile de funcționare cu 22°C și am prelungit durata de viață a componentelor la peste un an. Permiteți-mi să vă arăt cum am reușit - și cum puteți aplica aceleași principii la sistemele dumneavoastră.
Tabla de conținut
- Calcularea coeficientului de conducție: Cum se deplasează căldura prin componentele dumneavoastră?
- Metode de îmbunătățire a convecției: Ce tehnici maximizează transferul de căldură aer-suprafață?
- Modelul de eficiență a radiației: Când contează radiația termică în sistemele pneumatice?
- Concluzie
- Întrebări frecvente despre transferul de căldură în sistemele pneumatice
Calcularea coeficientului de conducție: Cum se deplasează căldura prin componentele dumneavoastră?
Conducția este principalul mecanism de transfer de căldură în cadrul componentelor pneumatice solide. Înțelegerea modului de calculare și optimizare a coeficienților de conducție este esențială pentru gestionarea temperaturilor sistemului.
Coeficientul de conducție termică poate fi calculat folosind Legea lui Fourier1: q = -k(dT/dx), unde q este fluxul de căldură (W/m²), k este conductivitatea termică (W/m-K), iar dT/dx este gradientul de temperatură. Pentru componentele pneumatice, conducția eficientă depinde de selectarea materialului, de calitatea interfeței și de factorii geometrici care afectează lungimea traseului termic și aria secțiunii transversale.
Îmi amintesc de depanarea unei linii de producție din Tennessee, unde rulmenții cilindrilor fără tijă cedau prematur. Echipa de întreținere încercase mai mulți lubrifianți fără succes. Când am analizat căile de conducție, am descoperit un blocaj termic la interfața dintre rulment și carcasă. Prin îmbunătățirea finisării suprafeței și aplicarea unui compus termoconductor, am crescut coeficientul de conducție efectivă cu 340% și am eliminat complet defecțiunile.
Ecuații fundamentale ale conducției
Să defalcăm ecuațiile cheie pentru calcularea conducției în componentele pneumatice:
Legea lui Fourier pentru conducția căldurii
Ecuația de bază care guvernează conducția căldurii este:
q = -k(dT/dx)
Unde:
- q = flux de căldură (W/m²)
- k = conductivitate termică (W/m-K)
- dT/dx = gradient de temperatură (K/m)
Pentru un caz simplu unidimensional cu secțiune transversală constantă:
Q = kA(T₁-T₂)/L
Unde:
- Q = rata transferului de căldură (W)
- A = Suprafața secțiunii transversale (m²)
- T₁, T₂ = Temperaturile la fiecare capăt (K)
- L = Lungimea traseului termic (m)
Conceptul de rezistență termică
Pentru geometrii complexe, abordarea rezistenței termice este adesea mai practică:
R = L/(kA)
Unde:
- R = rezistență termică (K/W)
Pentru sisteme cu mai multe componente în serie:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
Iar rata de transfer termic devine:
Q = ΔT/Rtotal
Compararea conductivității termice a materialelor
| Material | Conductivitate termică (W/m-K) | Conductivitate relativă | Aplicații comune |
|---|---|---|---|
| Aluminiu | 205-250 | Înaltă | Cilindri, radiatoare |
| Oțel | 36-54 | Mediu | Componente structurale |
| Oțel inoxidabil | 14-16 | Scăzut-Mediu | Medii corozive |
| Bronz | 26-50 | Mediu | Rulmenți, bucșe |
| PTFE | 0.25 | Foarte scăzut | Etanșări, rulmenți |
| Cauciuc nitrilic | 0.13 | Foarte scăzut | O-ringuri, garnituri |
| Aer (nemișcat) | 0.026 | Extrem de scăzut | Gap filler |
| Pastă termică | 3-8 | Scăzut | Material de interfață |
Rezistența la contact în ansamblurile pneumatice
La interfețele dintre componente, rezistența la contact afectează semnificativ transferul de căldură:
Rcontact = 1/(hc × A)
Unde:
- hc = Coeficient de contact (W/m²-K)
- A = Suprafața de contact (m²)
Factorii care afectează rezistența la contact includ:
- Rugozitatea suprafeței: Suprafețele mai aspre au o suprafață de contact reală mai mică
- Presiune de contact: O presiune mai mare crește suprafața de contact efectivă
- Materiale de interfață: Compușii termici umplu golurile de aer
- Curățenia suprafeței: Contaminanții pot crește rezistența
Studiu de caz: Optimizarea termică a cilindrilor fără tijă
Pentru un cilindru magnetic fără tijă care se confruntă cu probleme termice:
| Componentă | Design original | Design optimizat | Îmbunătățire |
|---|---|---|---|
| Corp cilindru | Aluminiu anodizat | Același material, finisaj îmbunătățit | 15% conducție mai bună |
| Interfața rulmentului | Contact metal-metal | Compus termic adăugat | 340% conducție mai bună |
| Suporturi de montare | Oțel vopsit | Aluminiu gol | 280% conducție mai bună |
| Rezistența termică generală | 2,8 K/W | 0,7 K/W | 75% reducere |
| Temperatura de funcționare | 78°C | 56°C | 22°C reducere |
| Durata de viață a componentei | 4 luni | >12 luni | 3× îmbunătățire |
Tehnici practice de optimizare a conducției
Pe baza experienței mele cu sute de sisteme pneumatice, iată care sunt cele mai eficiente abordări pentru îmbunătățirea conducției:
Optimizarea interfeței
- Finisarea suprafețelor: Îmbunătățirea netezimii suprafeței de contact la Ra 0,4-0,8 μm
- Materiale de interfață termică2: Aplicați compuși adecvați (3-8 W/m-K)
- Cuplu de strângere: Asigurați strângerea corectă pentru o presiune de contact optimă
- Curățenie: Îndepărtați toate uleiurile și contaminanții înainte de asamblare
Strategii de selecție a materialelor
- Căi termice critice: Utilizați materiale cu conductivitate ridicată (aluminiu, cupru)
- Întreruperi termice: Utilizați în mod intenționat materiale cu conductivitate scăzută pentru a izola căldura
- Abordări compozite: Combinați materialele pentru un raport performanță/cost optim
- Materiale anizotrope: Utilizați conductivitatea direcțională atunci când este cazul
Optimizarea geometrică
- Lungimea traseului termic: Minimizarea distanței dintre sursele de căldură și radiatoare
- Zona transversală: Maximizarea suprafeței perpendiculare pe fluxul de căldură
- Blocaje termice: Identificarea și eliminarea constrângerilor în calea căldurii
- Căi redundante: Crearea mai multor căi de conducție paralele
Metode de îmbunătățire a convecției: Ce tehnici maximizează transferul de căldură aer-suprafață?
Convecția este adesea factorul limitativ în răcirea sistemelor pneumatice. Îmbunătățirea transferului de căldură prin convecție poate îmbunătăți dramatic gestionarea termică și performanța sistemului.
Transferul de căldură convectiv urmează Legea răcirii a lui Newton3: Q = hA(Ts-T∞), unde h este coeficientul de convecție (W/m²-K), A este aria suprafeței, iar (Ts-T∞) este diferența de temperatură dintre suprafață și fluid. Metodele de îmbunătățire includ creșterea suprafeței prin aripioare, îmbunătățirea vitezei fluidului prin dirijarea fluxului de aer și optimizarea caracteristicilor suprafeței pentru a promova straturile limită turbulente.
În timpul unui audit al eficienței energetice la o instalație de ambalare din Arizona, am întâlnit un sistem pneumatic care funcționa într-un mediu ambiant de 43°C. Cilindrii fără tijă se supraîncălzeau, deși îndeplineau toate cerințele de întreținere. Prin punerea în aplicare a îmbunătățirii direcționate a convecției - adăugând mici aripioare de aluminiu și un ventilator cu consum redus de energie - am crescut coeficientul de convecție cu 450%. Acest lucru a redus temperaturile de funcționare de la niveluri periculoase la limitele specificate, fără modificări majore ale sistemului.
Bazele transferului de căldură prin convecție
Ecuația de bază care guvernează transferul convectiv de căldură este:
Q = hA(Ts-T∞)
Unde:
- Q = rata transferului de căldură (W)
- h = Coeficient de convecție (W/m²-K)
- A = Suprafața (m²)
- Ts = temperatura de suprafață (K)
- T∞ = Temperatura fluidului (aerului) (K)
Coeficientul de convecție h depinde de mai mulți factori:
- Proprietățile fluidelor (densitate, vâscozitate, conductivitate termică)
- Caracteristicile fluxului (viteză, turbulență)
- Geometria și orientarea suprafeței
- Regimul de curgere (convecție naturală vs. forțată)
Convecție naturală vs. forțată
| Parametru | Convecție naturală | Convecție forțată | Implicații |
|---|---|---|---|
| Valoare h tipică | 5-25 W/m²-K | 25-250 W/m²-K | Convecția forțată poate fi de 10× mai eficientă |
| Forța motrice | Flotabilitatea (diferența de temperatură) | Presiune externă (ventilatoare, suflante) | Convecția forțată este mai puțin dependentă de temperatură |
| Model de flux | Flux vertical de-a lungul suprafețelor | Direcțional pe baza mecanismului de forțare | Fluxul forțat poate fi optimizat pentru componente specifice |
| Fiabilitate | Pasiv, mereu prezent | Necesită energie și întreținere | Convecția naturală asigură răcirea de bază |
| Cerințe de spațiu | Necesită spațiu liber pentru circulația aerului | Necesită spațiu pentru instalații de aer condiționat și conducte | Sistemele forțate necesită mai multă planificare |
Tehnici de îmbunătățire a convecției
Augmentarea suprafeței
Creșterea suprafeței efective prin:
Aripioare și suprafețe extinse
- Pin aripioare: Fluxul de aer omnidirecțional, creșterea zonei 150-300%
- Aripioare cu plăci: Flux de aer direcțional, 200-500% creștere suprafață
- Suprafețe ondulate: Îmbunătățire moderată, creșterea suprafeței 50-150%Rugozitatea suprafeței
- Microtexturare: 5-15% creștere efectivă a suprafeței
- Suprafețe cu gropițe: creștere 10-30% plus efecte ale stratului limită
- Modele canelate: 15-40% crește cu beneficii direcționale
Manipularea fluxului
Îmbunătățirea caracteristicilor fluxului de aer prin:
Sisteme cu aer forțat
- Ventilatoare: flux de aer direcțional, 200-600% h îmbunătățire
- Suflante: Flux de înaltă presiune, 300-800% h îmbunătățire
- Jeturi de aer comprimat: Răcire direcționată, 400-1000% îmbunătățire locală hOptimizarea căii de curgere
- Deflectoare: Dirijează aerul către componentele critice
- Efecte Venturi: Accelerarea aerului pe anumite suprafețe
- Generatoare de vortexuri: Creați turbulențe pentru întreruperea stratului limită
Modificări ale suprafeței
Modificarea proprietăților suprafeței pentru a spori convecția:
Tratamente de emisivitate
- Oxid negru: Crește emisivitatea la 0,7-0,9
- Anodizare: Emisivitate controlată de la 0,4-0,9
- Vopsele și acoperiri: Emisivitate personalizabilă până la 0,98Controlul umezelii
- Acoperiri hidrofile: Îmbunătățesc răcirea lichidelor
- Suprafețe hidrofobe: Prevenirea problemelor de condensare
- Umezeală modelată: Curgere dirijată a condensului
Exemplu de implementare practică
Pentru un cilindru pneumatic fără tijă care funcționează într-un mediu cu temperatură ridicată:
| Metoda de îmbunătățire | Punerea în aplicare | h Îmbunătățire | Reducerea temperaturii |
|---|---|---|---|
| Pin Fins (6mm) | Aripioare clip-on din aluminiu, spațiere de 10 mm | 180% | 12°C |
| Flux de aer direcționat | Ventilator DC de 80 mm, 2 W la 1,5 m/s | 320% | 18°C |
| Tratarea suprafeței | Anodizare neagră | 40% | 3°C |
| Abordare combinată | Toate metodele integrate | 450% | 24°C |
Corelația numărului Nusselt pentru calculele de proiectare
Pentru calculele tehnice, valoarea Numărul Nusselt4 (Nu) oferă o abordare adimensională a convecției:
Nu = hL/k
Unde:
- L = Lungimea caracteristică
- k = Conductivitatea termică a fluidului
Pentru convecția forțată peste o placă plană:
Nu = 0,664Re^(1/2)Pr^(1/3) (flux laminar)
Nu = 0,037Re^(4/5)Pr^(1/3) (curgere turbulentă)
Unde:
- Re = numărul Reynolds (viteză × lungime × densitate / vâscozitate)
- Pr = numărul Prandtl (căldură specifică × vâscozitate / conductivitate termică)
Aceste corelații permit inginerilor să prezică coeficienții de convecție pentru diferite configurații și să optimizeze strategiile de răcire în consecință.
Modelul de eficiență a radiației: Când contează radiația termică în sistemele pneumatice?
Radiația este adesea neglijată în gestionarea termică a sistemelor pneumatice, dar poate reprezenta 15-30% din transferul total de căldură în multe aplicații. Înțelegerea momentului și a modului de optimizare a transferului de căldură prin radiație este esențială pentru gestionarea termică cuprinzătoare.
Transferul de căldură prin radiație urmează principiul Legea Stefan-Boltzmann5: Q = εσA(T₁⁴-T₂⁴), unde ε este emisivitatea suprafeței, σ este constanta Stefan-Boltzmann, A este aria suprafeței, iar T₁ și T₂ sunt temperaturile absolute ale suprafeței de emisie și ale mediului înconjurător. Eficiența radiației în sistemele pneumatice depinde în primul rând de emisivitatea suprafeței, de diferența de temperatură și de factorii de vizualizare dintre componente și mediul lor.
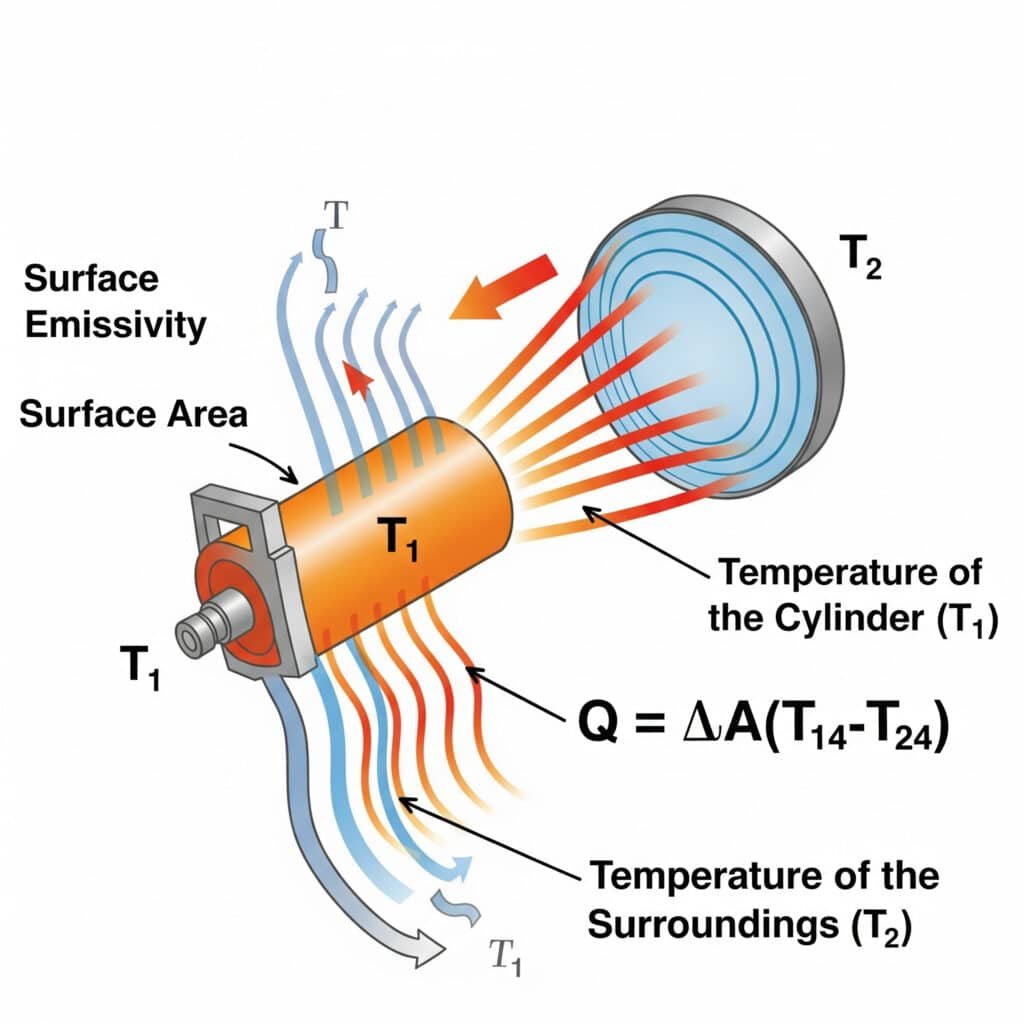
Am ajutat recent un producător de echipamente semiconductoare din Oregon să rezolve problemele de supraîncălzire ale cilindrilor lor de precizie fără tijă. Inginerii lor se axaseră exclusiv pe conducție și convecție, dar neglijaseră radiația. Prin aplicarea unui strat cu emisivitate ridicată (crescând ε de la 0,11 la 0,92), am îmbunătățit transferul de căldură prin radiație cu peste 700%. Această soluție simplă și pasivă a redus temperaturile de funcționare cu 9°C, fără piese în mișcare sau consum de energie - o cerință esențială în mediul lor de cameră sterilă.
Fundamentele transferului de căldură prin radiație
Ecuația de bază care guvernează transferul radiativ de căldură este:
Q = εσA(T₁⁴-T₂⁴)
Unde:
- Q = rata transferului de căldură (W)
- ε = Emisivitate (fără dimensiuni, 0-1)
- σ = constanta Stefan-Boltzmann (5,67 × 10-⁸ W/m²-K⁴)
- A = Suprafața (m²)
- T₁ = Temperatura absolută a suprafeței (K)
- T₂ = Temperatura absolută a mediului înconjurător (K)
Valori ale emisivității suprafeței pentru materiale pneumatice comune
| Material/Suprafață | Emisivitate (ε) | Eficiența radiației | Potențial de îmbunătățire |
|---|---|---|---|
| Aluminiu lustruit | 0.04-0.06 | Foarte slabă | >1500% îmbunătățire posibilă |
| Aluminiu anodizat | 0.7-0.9 | Excelentă | Deja optimizat |
| Oțel inoxidabil (lustruit) | 0.07-0.14 | Slabă | >600% îmbunătățire posibilă |
| Oțel inoxidabil (oxidat) | 0.6-0.85 | Bun | Este posibilă o ameliorare moderată |
| Oțel (lustruit) | 0.07-0.10 | Slabă | >900% îmbunătățire posibilă |
| Oțel (oxidat) | 0.7-0.9 | Excelentă | Deja optimizat |
| Suprafețe vopsite | 0.8-0.98 | Excelentă | Deja optimizat |
| PTFE (alb) | 0.8-0.9 | Excelentă | Deja optimizat |
| Cauciuc nitrilic | 0.86-0.94 | Excelentă | Deja optimizat |
Considerații privind factorul de vizualizare
Schimbul de radiații depinde nu numai de emisivitate, ci și de relațiile geometrice dintre suprafețe:
F₁₂ = Fracțiunea de radiație care părăsește suprafața 1 și lovește suprafața 2
Pentru geometrii complexe, factorii de vizualizare pot fi calculați folosind:
- Soluții analitice pentru geometrii simple
- Vezi algebra factorului pentru combinarea soluțiilor cunoscute
- Metode numerice pentru aranjamente complexe
- Aproximări empirice pentru inginerie practică
Dependența de temperatură a radiației
Relația de temperatură de a patra putere face ca radiațiile să fie deosebit de eficiente la temperaturi ridicate:
| Temperatura de suprafață | Procentul de transfer de căldură prin radiație* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
* Presupunând condiții de convecție naturală, ε = 0,8, 25°C mediu
Strategii de îmbunătățire a eficienței radiațiilor
Pe baza experienței mele cu sistemele pneumatice industriale, iată care sunt cele mai eficiente abordări pentru îmbunătățirea transferului de căldură prin radiație:
Modificarea emisivității suprafeței
Acoperiri cu emisivitate ridicată
- Anodizare neagră pentru aluminiu (ε ≈ 0,8-0,9)
- Oxid negru pentru oțel (ε ≈ 0,7-0,8)
- Acoperiri ceramice speciale (ε ≈ 0,9-0,98)Texturarea suprafețelor
- Micro-rugozitatea crește emisivitatea efectivă
- Suprafețele poroase îmbunătățesc proprietățile radiative
- Îmbunătățiri combinate ale emisivității/convecției
Optimizarea mediului
Gestionarea temperaturii în jur
- Izolarea de echipamente/procese fierbinți
- Pereți/plafoane reci pentru un schimb mai bun de radiații
- Bariere reflectorizante pentru direcționarea radiațiilor către suprafețe mai reciVezi îmbunătățirea factorului
- Orientare pentru a maximiza expunerea la suprafețe reci
- Îndepărtarea obiectelor care blochează
- Reflectoare pentru îmbunătățirea schimbului de radiații cu zonele mai reci
Studiu de caz: Îmbunătățirea radiațiilor în pneumatica de precizie
Pentru un cilindru fără tijă de înaltă precizie într-un mediu de cameră curată:
| Parametru | Design original | Proiectare îmbunătățită prin radiații | Îmbunătățire |
|---|---|---|---|
| Material de suprafață | Aluminiu lustruit (ε ≈ 0.06) | Aluminiu acoperit cu ceramică (ε ≈ 0,94) | 1467% creșterea emisivității |
| Transferul de căldură prin radiație | 2.1W | 32.7W | 1457% creștere în radiații |
| Temperatura de funcționare | 68°C | 59°C | 9°C reducere |
| Durata de viață a componentei | 8 luni | >24 luni | 3× îmbunătățire |
| Costuri de implementare | – | $175 pe cilindru | Recuperare în 4,2 luni |
Radiația vs. alte moduri de transfer al căldurii
Înțelegerea momentului în care radiațiile domină este esențială pentru gestionarea eficientă a căldurii:
| Stare | Dominanța conducerii | Dominanța convecției | Dominanța radiațiilor |
|---|---|---|---|
| Intervalul de temperatură | De la scăzut la ridicat | De la scăzut la mediu | De la mediu la ridicat |
| Proprietăți materiale | Materiale cu k ridicat | K scăzut, suprafață mare | Suprafețe cu ε ridicat |
| Factori de mediu | Contact termic bun | Aer în mișcare, ventilatoare | Diferență mare de temperatură |
| Constrângeri de spațiu | Ambalare strânsă | Flux de aer deschis | Vedere la împrejurimile mai reci |
| Cele mai bune aplicații | Interfețe componente | Răcire generală | Suprafețe fierbinți, vid, aer liniștit |
Concluzie
Stăpânirea principiilor transferului de căldură - calculul coeficientului de inducție, metodele de îmbunătățire a convecției și modelarea eficienței radiației - oferă baza pentru gestionarea termică eficientă în sistemele pneumatice. Prin aplicarea acestor principii, puteți reduce temperaturile de funcționare, prelungi durata de viață a componentelor și îmbunătăți eficiența energetică, asigurând în același timp funcționarea fiabilă chiar și în medii dificile.
Întrebări frecvente despre transferul de căldură în sistemele pneumatice
Care este creșterea tipică a temperaturii în cilindrii pneumatici în timpul funcționării?
Cilindrii pneumatici înregistrează de obicei creșteri de temperatură de 20-40°C peste temperatura ambiantă în timpul funcționării continue. Această creștere rezultă din frecarea dintre garnituri și pereții cilindrului, încălzirea aerului prin compresie și transformarea muncii mecanice în căldură. Cilindrii fără tijă înregistrează adesea creșteri de temperatură mai mari (30-50°C) din cauza sistemelor de etanșare mai complexe și a generării concentrate de căldură în ansamblul rulment/etanșare.
Cum afectează presiunea de funcționare generarea de căldură în sistemele pneumatice?
Presiunea de funcționare are un impact semnificativ asupra generării de căldură, presiunile mai mari generând mai multă căldură prin mai multe mecanisme. Fiecare creștere cu 1 bar a presiunii de funcționare crește, de obicei, generarea de căldură cu 8-12% din cauza forțelor de frecare mai mari între garnituri și suprafețe, a încălzirii prin compresie mai mari și a pierderilor crescute legate de scurgeri. Această relație este aproximativ liniară în intervalele normale de funcționare (3-10 bar).
Care este abordarea optimă de răcire pentru componentele pneumatice în diferite medii?
Metoda optimă de răcire variază în funcție de mediu: în medii curate, cu temperaturi moderate (15-30°C), convecția naturală cu distanța corespunzătoare între componente este adesea suficientă. În medii cu temperaturi ridicate (30-50°C), devine necesară convecția forțată cu ajutorul ventilatoarelor sau al aerului comprimat. În condiții extrem de fierbinți (>50°C) sau atunci când fluxul de aer este restricționat, pot fi necesare metode active de răcire, cum ar fi răcitoarele termoelectrice sau răcirea cu lichid. În toate cazurile, maximizarea radiației prin suprafețe cu emisivitate ridicată asigură o răcire pasivă suplimentară.
Cum se calculează transferul total de căldură de la o componentă pneumatică?
Calculați transferul total de căldură prin însumarea contribuțiilor fiecărui mecanism: Qtotal = Qconducție + Qconvecție + Qradiație. Pentru conducție, utilizați Q = kA(T₁-T₂)/L pentru fiecare cale termică. Pentru convecție, se utilizează Q = hA(Ts-T∞) cu coeficienții de convecție corespunzători. Pentru radiație, se utilizează Q = εσA(T₁⁴-T₂⁴). În majoritatea aplicațiilor pneumatice industriale care funcționează la 30-80°C, distribuția aproximativă este 20-40% conducție, 40-70% convecție și 10-30% radiație.
Care este relația dintre temperatură și durata de viață a componentelor pneumatice?
Durata de viață a componentelor scade exponențial odată cu creșterea temperaturii, urmând o relație Arrhenius modificată. Ca regulă generală, fiecare creștere cu 10°C a temperaturii de funcționare reduce durata de viață a garniturilor și a componentelor cu 40-50%. Aceasta înseamnă că o componentă care funcționează la 70°C poate dura doar o treime din durata aceleiași componente la 50°C. Această relație este deosebit de critică pentru componentele polimerice precum garniturile de etanșare, rulmenții și garniturile, care determină adesea intervalul de întreținere pentru sistemele pneumatice.
-
Oferă o explicație fundamentală a legii lui Fourier, principiul fundamental care descrie modul în care căldura este condusă prin materiale solide pe baza conductivității termice și a gradientului de temperatură. ↩
-
Explică funcția și tipurile de materiale de interfață termică (TIM), care sunt utilizate pentru a umple golurile de aer microscopice dintre componente pentru a îmbunătăți conducerea căldurii și a reduce rezistența termică. ↩
-
Detaliază principiile Legii răcirii a lui Newton, care guvernează modul în care obiectele se răcesc prin transferul căldurii către fluidul înconjurător prin convecție, un factor cheie în proiectarea sistemelor de răcire. ↩
-
Oferă o privire aprofundată asupra numărului Nusselt, o mărime adimensională critică în dinamica fluidelor și transferul de căldură, care reprezintă raportul dintre transferul de căldură convectiv și conductiv printr-o limită. ↩
-
Descrie legea Stefan-Boltzmann, principiul fizic fundamental care cuantifică energia totală radiată de un corp negru, care este esențială pentru calcularea pierderilor de căldură de pe suprafețe fierbinți. ↩


