Cum influențează rezonanța vibrațiilor performanța echipamentelor industriale?

Coșmarul oricărui inginer de întreținere este defectarea neașteptată a echipamentelor. Atunci când mașinile vibrează la frecvența lor naturală, pot apărea daune catastrofale în câteva minute. Am văzut cum această problemă a costat companiile mii de euro în timpi morți.

Rezonanța vibrațiilor¹ apare atunci când o forță externă se potrivește cu frecvența naturală a unui sistem, provocând oscilații amplificate care pot deteriora echipamentele. Înțelegerea și controlul acestui fenomen sunt esențiale pentru prevenirea defecțiunilor și prelungirea duratei de viață a utilajelor.

Permiteți-mi să împărtășesc o scurtă poveste. Anul trecut, un client din Germania m-a sunat în panică. Linia lor de producție se oprise deoarece un cilindru fără tijă vibra violent. Problema? Rezonanța. Până la sfârșitul acestui articol, veți înțelege cum să identificați și să preveniți probleme similare în sistemele dumneavoastră.

Tabla de conținut

Formula frecvenței naturale: Cum puteți calcula punctele vulnerabile ale sistemului dumneavoastră?
Modelul Mass-Spring: De ce este atât de valoroasă această abordare simplificată?
Optimizarea raportului de amortizare: Ce experimente dau cele mai bune rezultate?
Concluzie
Întrebări frecvente despre rezonanța vibrațiilor

Formula frecvenței naturale: Cum puteți calcula punctele vulnerabile ale sistemului dumneavoastră?

Înțelegerea frecvenței naturale a echipamentului dumneavoastră este primul pas către prevenirea problemelor de rezonanță. Această valoare critică determină momentul în care sistemul dvs. este cel mai vulnerabil la probleme de vibrații.

The frecvența naturală² (fn) a unui sistem poate fi calculată folosind formula: fn = (1/2π) × √(k/m), unde k este coeficientul de rigiditate și m este masa. Acest calcul relevă frecvența la care sistemul dumneavoastră va rezona dacă este excitat de forțe externe corespunzătoare.

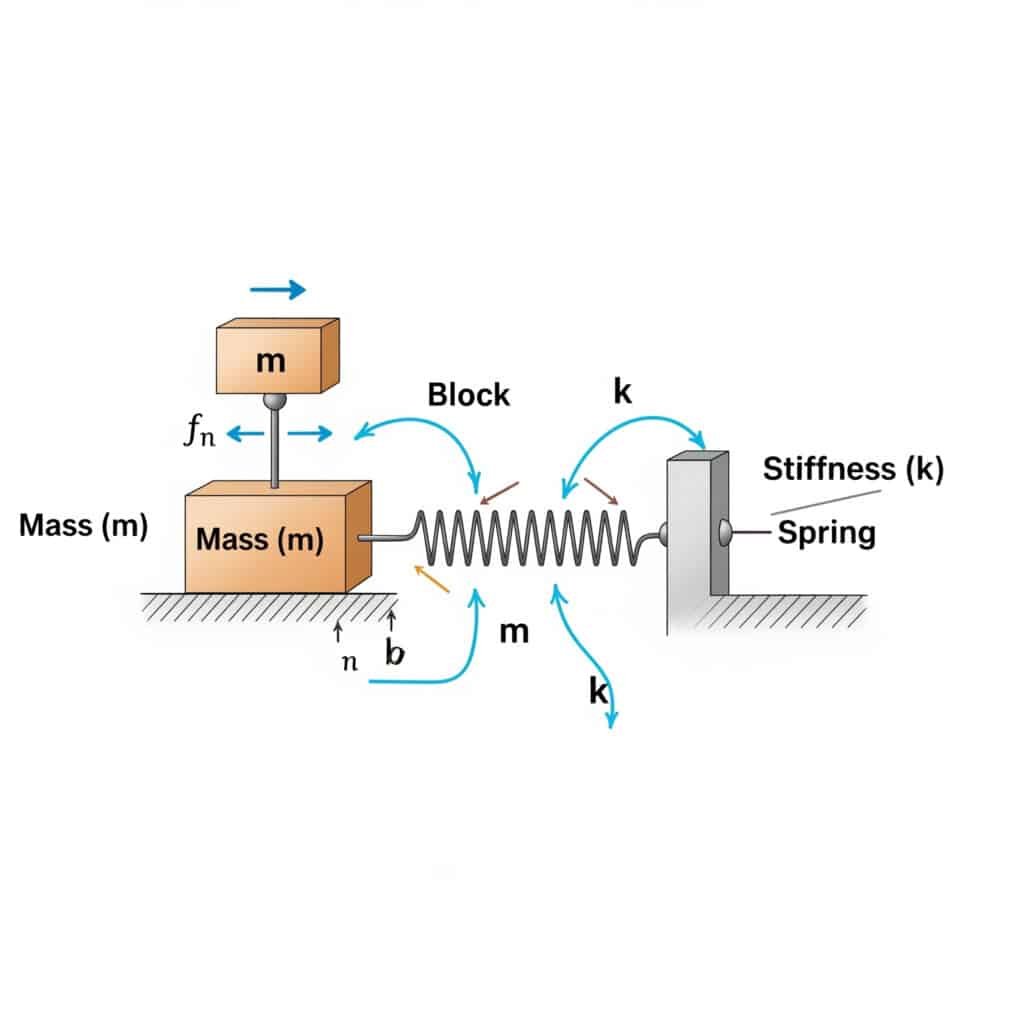
O diagramă clară, educativă, care explică frecvența naturală. Ilustrația prezintă un sistem simplu masă- resort, cu blocul etichetat "Masa (m)" și resortul etichetat "Rigiditatea (k)". Liniile de mișcare arată că sistemul oscilează. Adiacent diagramei, formula "fn = (1/2π) × √(k/m)" este afișată în mod clar, cu săgeți care leagă explicit variabilele "m" și "k" din ecuație de părțile fizice corespunzătoare. — frecvența naturală

Când am vizitat o fabrică din Elveția, am observat că cilindrii lor pneumatici fără tijă cedează prematur. Echipa lor de întreținere nu calculase frecvența naturală a instalației lor. După ce am aplicat această formulă, am identificat că viteza lor de funcționare era periculos de aproape de frecvența naturală a sistemului.

Aplicații practice ale calculelor frecvenței naturale

Formula frecvenței naturale nu este doar teoretică - are aplicații directe în diverse contexte industriale:

Selectarea echipamentului: Alegerea componentelor cu frecvențe naturale departe de condițiile dumneavoastră de funcționare
Întreținere preventivă: Programarea inspecțiilor pe baza profilurilor de risc de vibrații
Rezolvarea problemelor: Identificarea cauzei de bază a vibrațiilor neașteptate

Valori comune ale frecvenței naturale pentru componentele industriale

Componentă	Interval de frecvență naturală tipică (Hz)
Cilindri fără tijă	10-50 Hz
Suporturi de montare	20-100 Hz
Structuri de sprijin	5-30 Hz
Supape de control	40-200 Hz

Factori critici care afectează frecvența naturală

Calculul frecvenței naturale pare simplu, dar mai mulți factori pot complica aplicațiile din lumea reală:

Distribuția neuniformă a masei: Majoritatea componentelor industriale nu au masa perfect distribuită
Rigiditate variabilă: Componentele pot avea rigiditate diferită în direcții diferite
Puncte de conectare: Modul în care sunt montate componentele afectează în mod semnificativ caracteristicile lor de vibrație
Efectele temperaturii: Atât masa, cât și rigiditatea se pot modifica în funcție de temperatură

Modelul Mass-Spring: De ce este atât de valoroasă această abordare simplificată?

Modelul masă-remurs oferă un cadru intuitiv pentru înțelegerea sistemelor complexe de vibrații. Acesta reduce mașinile complicate la elemente de bază pe care inginerii le pot analiza cu ușurință.

The modelul masă-moslă³ simplifică analiza vibrațiilor prin reprezentarea sistemelor mecanice ca mase discrete conectate prin arcuri. Această abordare permite inginerilor să prezică comportamentul sistemului, să identifice potențialele probleme de rezonanță și să dezvolte soluții eficiente fără matematică complexă.

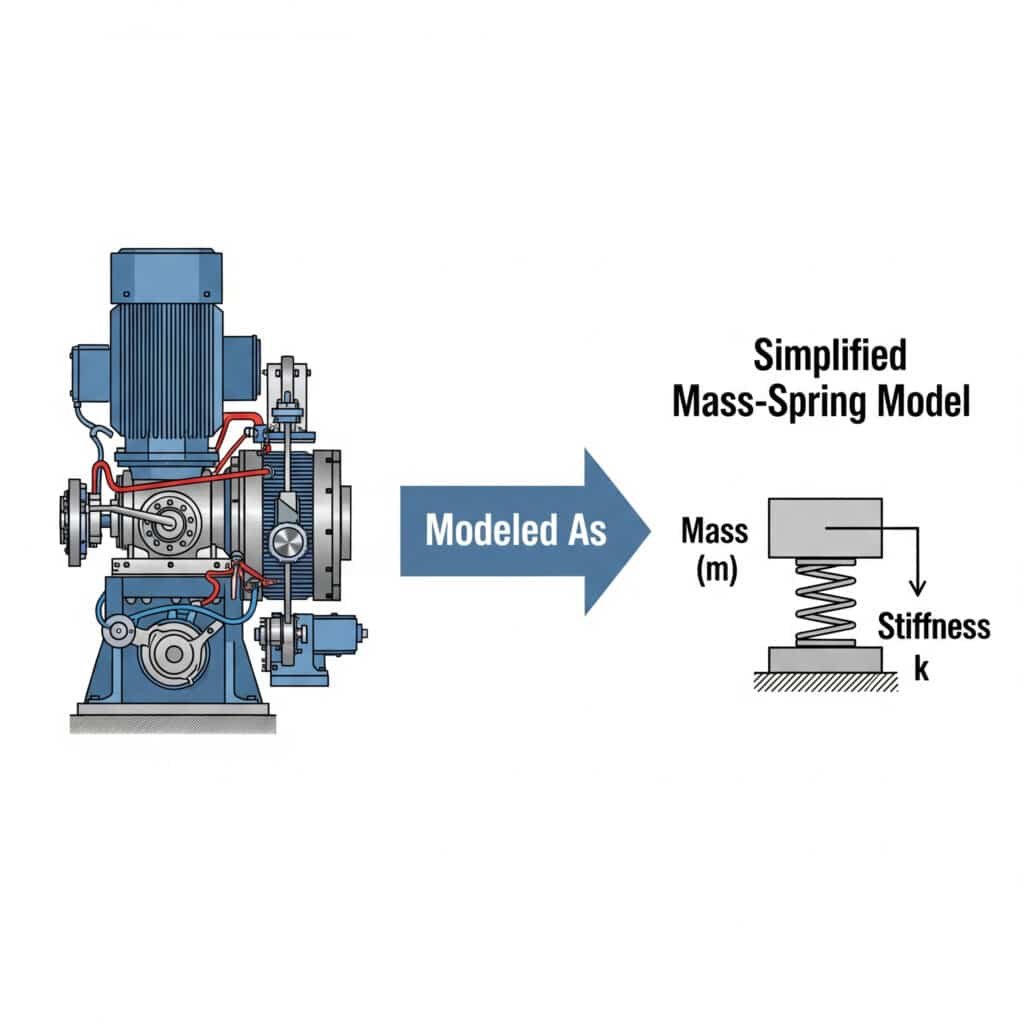
Un infografic comparativ care explică modelul masă-remorcă. În stânga, sub eticheta "Sistem mecanic complex", se află o ilustrare detaliată a unui motor industrial. O săgeată mare etichetată "Modelat ca" indică spre dreapta. În dreapta, sub eticheta "Model simplificat masă- resort", întregul motor complex este reprezentat de un bloc simplu etichetat "Masă (m)" conectat la un resort simplu etichetat "Rigiditate (k)". — modelul masă-moslă

Îmi amintesc că am lucrat cu un producător de piese auto din Michigan care nu înțelegea de ce cilindrii lor fără tijă ghidată cedau. Prin modelarea sistemului lor ca un aranjament simplu masă- resort, am identificat faptul că suporturile de montare acționau ca resorturi neintenționate, creând o stare de rezonanță.

Conversia sistemelor reale în modele de izvoare de masă

Pentru a aplica această abordare la echipamentul dvs:

Identificarea maselor cheie: Determinarea componentelor care contribuie semnificativ la greutate
Localizați elementele de arc: Găsiți componente care stochează și eliberează energie (arcuri reale, suporturi flexibile etc.)
Conexiuni pe hartă: Documentați modul în care interacționează masele și arcurile
Simplificați: Combinarea elementelor similare pentru a crea un model ușor de gestionat

Tipuri de sisteme Mass-Spring

Tip de sistem	Descriere	Aplicații comune
DOF unic	O masă cu un arc	Cilindri pneumatici simpli
Multi-DOF	Mase multiple cu arcuri multiple	Mașini complexe cu mai multe componente
Continuă	DOF infinit (necesită o analiză diferită)	Grinzi, plăci și învelișuri

Considerații privind modelarea avansată

În timp ce modelul de bază masă-musculă este valoros, câteva îmbunătățiri îl fac mai realist:

Adăugarea amortizoarelor: Sistemele reale au întotdeauna disipare de energie
Luarea în considerare a neliniarităților: Izvoarele nu urmează întotdeauna Legea lui Hooke⁴ perfect
Contabilizarea vibrațiilor forțate: Forțele externe modifică comportamentul sistemului
Inclusiv efectele de cuplare: Mișcarea într-o direcție poate afecta alte direcții

Optimizarea raportului de amortizare: Ce experimente dau cele mai bune rezultate?

Amortizarea este cea mai bună apărare împotriva problemelor de rezonanță. Găsirea raportului optim de amortizare prin experimentare poate îmbunătăți dramatic performanța și fiabilitatea sistemului.

Raport de amortizare⁵ experimentele de optimizare implică testarea sistematică a diferitelor configurații de amortizare pentru a găsi echilibrul ideal între controlul vibrațiilor și capacitatea de reacție a sistemului. Raportul optim de amortizare se situează de obicei între 0,2 și 0,7, oferind o suprimare suficientă a vibrațiilor fără pierderi excesive de energie.

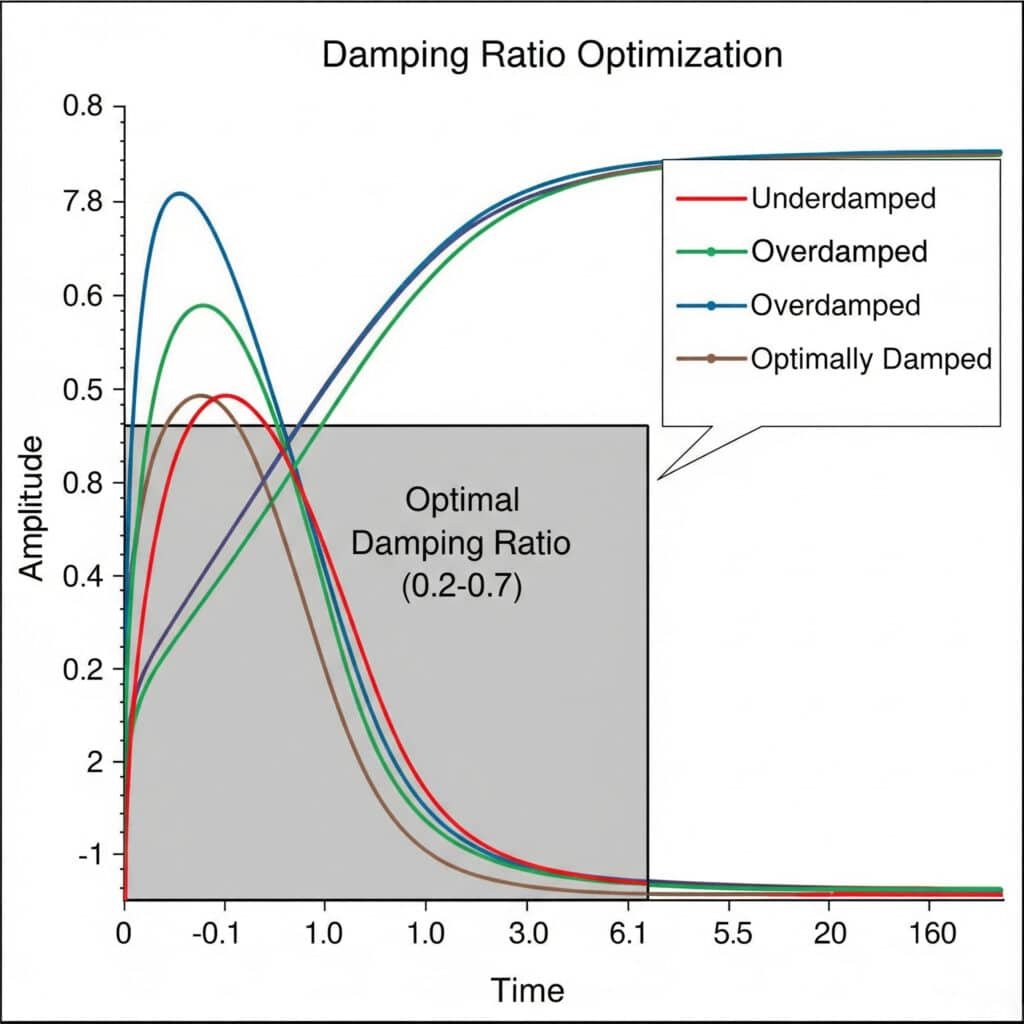
Un grafic care ilustrează optimizarea raportului de amortizare prin trasarea "Amplitudinii" sistemului în funcție de "Timp". Acesta afișează trei curbe de răspuns distincte: o curbă "subamortizată" care oscilează semnificativ, o curbă "supraamortizată" care revine la zero foarte lent, fără oscilații, și o curbă "amortizată optim" care se stabilizează rapid cu o depășire minimă. O regiune umbrită evidențiază acest răspuns ideal, etichetată "Raport de amortizare optim (0,2-0,7)". — optimizarea raportului de amortizare

Luna trecută, am ajutat un producător de echipamente de procesare a alimentelor din Franța să rezolve problemele de vibrații persistente ale cilindrilor lor magnetici fără tijă. Printr-o serie de experimente privind raportul de amortizare, am descoperit că proiectul lor inițial avea un raport de amortizare de numai 0,05 - mult prea mic pentru a preveni problemele de rezonanță.

Configurație experimentală pentru testarea raportului de amortizare

Pentru a efectua experimente eficiente de optimizare a amortizării:

Măsurarea inițială: Înregistrați răspunsul sistemului fără amortizare suplimentară
Testarea incrementală: Adăugați elemente de amortizare în creșteri controlate
Măsurarea răspunsului: Măsurați amplitudinea, timpul de stabilizare și răspunsul la frecvență
Analiza datelor: Calculați raportul de amortizare pentru fiecare configurație
Validare: Verificați performanța în condiții reale de funcționare

Comparație între tehnologiile de amortizare

Tehnologie de amortizare	Avantaje	Limitări	Aplicații tipice
Amortizoare vâscoase	Performanță previzibilă, temperatură stabilă	Necesită întreținere, scurgeri potențiale	Utilaje grele, echipamente de precizie
Amortizoare de fricțiune	Design simplu, rentabil	Uzură în timp, comportament neliniar	Suporturi structurale, utilaje de bază
Material Amortizare	Fără părți mobile, compact	Interval de reglare limitat	Instrumente de precizie, izolarea vibrațiilor
Amortizare activă	Adaptabil la condițiile în schimbare	Complex, necesită putere	Aplicații critice, echipamente cu viteză variabilă

Optimizarea amortizării pentru diferite condiții de funcționare

Raportul ideal de amortizare nu este universal - depinde de aplicația dvs. specifică:

Operațiuni de mare viteză: Raporturile de amortizare mai mici (0,1-0,3) mențin capacitatea de reacție
Aplicații de precizie: Raporturile de amortizare mai mari (0,5-0,7) oferă stabilitate
Sisteme cu încărcare variabilă: Amortizarea adaptivă poate fi necesară
medii sensibile la temperatură: Luați în considerare materialele de amortizare cu proprietăți stabile

Studiu de caz: Optimizarea amortizării cilindrilor fără tijă

La optimizarea unui cilindru fără tijă cu dublu efect pentru o mașină de ambalat, am testat cinci configurații diferite de amortizare:

Perne de capăt standard: Raport de amortizare = 0,12
Perne extinse: Raport de amortizare = 0,25
Amortizoare externe: Raport de amortizare = 0,41
Suporturi de montare din material compozit: Raport de amortizare = 0,38
Abordare combinată (3+4): Raport de amortizare = 0,53

Abordarea combinată a oferit cea mai bună performanță, reducând amplitudinea vibrațiilor cu 78% și menținând în același timp timpi de răspuns acceptabili.

Concluzie

Înțelegerea rezonanței vibrațiilor prin calcularea frecvenței naturale, modelarea masei și arcurilor și optimizarea raportului de amortizare este esențială pentru prevenirea defecțiunilor echipamentelor. Prin aplicarea acestor principii, puteți prelungi durata de viață a utilajelor, reduce timpii morți și îmbunătăți performanța generală a sistemului.

Întrebări frecvente despre rezonanța vibrațiilor

Ce este rezonanța vibrațiilor în echipamentele industriale?

Rezonanța vibrațiilor apare atunci când o forță externă se potrivește cu frecvența naturală a unui sistem, provocând oscilații amplificate. În cazul echipamentelor industriale, acest fenomen poate duce la mișcări excesive, oboseală a componentelor și defecțiuni catastrofale dacă nu este gestionat corespunzător.

Cum pot identifica dacă sistemul meu se confruntă cu rezonanță?

Căutați simptome precum creșterea inexplicabilă a zgomotului, vibrații vizibile la anumite viteze, defecțiuni premature ale componentelor și degradarea performanțelor care apare la puncte de funcționare constante. Instrumentele de analiză a vibrațiilor pot confirma condițiile de rezonanță.

Care este diferența dintre vibrația forțată și rezonanță?

Vibrația forțată apare ori de câte ori o forță externă acționează asupra unui sistem, în timp ce rezonanța este condiția specifică în care frecvența forțată coincide cu frecvența naturală a sistemului, rezultând un răspuns amplificat. Toate rezonanțele implică vibrații forțate, dar nu toate vibrațiile forțate cauzează rezonanță.

Cum influențează proiectarea unui cilindru pneumatic fără tijă caracteristicile sale de vibrație?

Proiectarea cilindrilor pneumatici fără tijă - cu căruciorul lor mobil, sistemul intern de etanșare și mecanismele de ghidare - creează provocări unice legate de vibrații. Profilul extins acționează ca o grindă care se poate îndoi, masa căruciorului creează forțe inerțiale, iar benzile de etanșare pot introduce o frecare variabilă.

Ce modificări simple pot reduce rezonanța în echipamentele existente?

Pentru echipamentele existente care se confruntă cu probleme de rezonanță, luați în considerare adăugarea de masă pentru a modifica frecvența naturală, instalarea de amortizoare externe sau de amortizoare de șocuri, modificarea metodelor de montare pentru a include izolarea împotriva vibrațiilor sau ajustarea vitezelor de funcționare pentru a evita frecvențele de rezonanță.

Oferă o explicație fundamentală a rezonanței mecanice, adesea cu exemple vizuale, demonstrând cum o forță periodică mică poate produce oscilații de amplitudine mare într-un sistem. ↩
Oferă o privire detaliată asupra fizicii frecvenței naturale, frecvența specifică la care un sistem tinde să oscileze în absența oricărei forțe motrice sau de amortizare. ↩
Explică principiile modelului masă-rezort, o idealizare fundamentală în fizică și inginerie utilizată pentru a analiza sisteme complexe care prezintă o mișcare armonică simplă. ↩
Detalii Legea lui Hooke, un principiu al fizicii care afirmă că forța necesară pentru a extinde sau comprima un arc pe o anumită distanță este direct proporțională cu acea distanță. ↩
Descrie raportul de amortizare, o măsură adimensională care definește modul în care oscilațiile unui sistem scad după o perturbare, ceea ce este esențial pentru controlul rezonanței. ↩

Bună ziua, sunt Chuck, un expert senior cu 15 ani de experiență în industria pneumatică. La Bepto Pneumatic, mă concentrez pe furnizarea de soluții pneumatice de înaltă calitate, personalizate pentru clienții noștri. Expertiza mea acoperă automatizarea industrială, proiectarea și integrarea sistemelor pneumatice, precum și aplicarea și optimizarea componentelor cheie. Dacă aveți întrebări sau doriți să discutați nevoile proiectului dumneavoastră, nu ezitați să mă contactați la chuck@bepto.com.