
Вы когда-нибудь прикасались к пневматический цилиндр После длительной эксплуатации вы были удивлены тем, насколько горячо? Этот жар - не просто неудобство, а напрасная трата энергии, снижение эффективности и потенциальные проблемы с надежностью, которые могут стоить вашему предприятию тысячи.
Теплопередача в пневматических системах происходит по трем механизмам: теплопроводность через материалы компонентов, конвекция между поверхностями и воздухом, а также излучение от горячих поверхностей. Понимание и оптимизация этих принципов позволяет снизить рабочую температуру на 15-30%, продлить срок службы компонентов до 40% и повысить энергоэффективность на 5-15%.
В прошлом месяце я консультировал предприятие пищевой промышленности в Джорджии, где бесштоковые цилиндры выходили из строя каждые 3-4 месяца из-за тепловых проблем. Их команда технического обслуживания просто заменяла компоненты, не устраняя первопричину. Применив принципы правильной теплопередачи, мы снизили рабочую температуру на 22 °C и увеличили срок службы компонентов более чем на год. Позвольте мне показать вам, как мы это сделали, и как вы можете применить эти же принципы в своих системах.
Оглавление
- Расчет коэффициента проводимости: Как тепло перемещается через ваши компоненты?
- Методы усиления конвекции: Какие методы обеспечивают максимальный теплообмен между воздухом и поверхностью?
- Модель радиационной эффективности: Когда тепловое излучение имеет значение в пневматических системах?
- Заключение
- Вопросы и ответы о теплопередаче в пневматических системах
Расчет коэффициента проводимости: Как тепло перемещается через ваши компоненты?
Теплопроводность является основным механизмом передачи тепла в твердых пневматических компонентах. Понимание того, как рассчитать и оптимизировать коэффициенты теплопроводности, необходимо для управления температурой системы.
Коэффициент теплопроводности можно рассчитать, используя Закон Фурье1: q = -k(dT/dx), где q - тепловой поток (Вт/м²), k - теплопроводность (Вт/м-К), а dT/dx - градиент температуры. Для пневматических компонентов эффективная теплопроводность зависит от выбора материала, качества интерфейса и геометрических факторов, влияющих на длину и площадь поперечного сечения теплового пути.
Я помню, как устранял неполадки на производственной линии в Теннесси, где преждевременно выходили из строя подшипники бесштоковых цилиндров. Команда технического обслуживания безуспешно пробовала множество смазочных материалов. Когда мы проанализировали проводящие пути, то обнаружили тепловое узкое место на стыке подшипника и корпуса. Улучшив качество обработки поверхности и нанеся теплопроводящий компаунд, мы увеличили эффективный коэффициент теплопроводности на 340% и полностью устранили отказы.
Фундаментальные уравнения проводимости
Давайте разберем основные уравнения для расчета проводимости в пневматических компонентах:
Закон Фурье для теплопроводности
Основное уравнение, определяющее теплопроводность, таково:
q = -k(dT/dx)
Где:
- q = Тепловой поток (Вт/м²)
- k = Теплопроводность (Вт/м-К)
- dT/dx = градиент температуры (К/м)
Для простого одномерного случая с постоянным сечением:
Q = kA(T₁-T₂)/L
Где:
- Q = скорость теплопередачи (Вт)
- A = площадь поперечного сечения (м²)
- T₁, T₂ = температура на каждом конце (K)
- L = длина теплового пути (м)
Концепция термического сопротивления
Для сложных геометрических форм подход, основанный на термическом сопротивлении, часто оказывается более практичным:
R = L/(kA)
Где:
- R = термическое сопротивление (К/Вт)
Для систем с несколькими последовательно соединенными компонентами:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
И скорость теплопередачи становится:
Q = ΔT/Rtotal
Сравнение теплопроводности материалов
| Материал | Теплопроводность (Вт/м-К) | Относительная проводимость | Общие приложения |
|---|---|---|---|
| Алюминий | 205-250 | Высокий | Цилиндры, радиаторы |
| Сталь | 36-54 | Средний | Структурные компоненты |
| Нержавеющая сталь | 14-16 | Низкий-средний | Коррозионные среды |
| Бронза | 26-50 | Средний | Подшипники, втулки |
| PTFE | 0.25 | Очень низкий | Уплотнения, подшипники |
| Нитриловая резина | 0.13 | Очень низкий | О-ринги, уплотнения |
| Воздух (неподвижный) | 0.026 | Крайне низкий | Заполнитель зазоров |
| Термопаста | 3-8 | Низкий | Материал интерфейса |
Контактное сопротивление в пневматических узлах
На границах между компонентами контактное сопротивление существенно влияет на теплопередачу:
Rконт = 1/(hc × A)
Где:
- hc = коэффициент контакта (Вт/м²-K)
- A = площадь контакта (м²)
Факторы, влияющие на сопротивление контакта, включают:
- Шероховатость поверхности: Шероховатые поверхности имеют меньшую площадь фактического контакта
- Контактное давление: Более высокое давление увеличивает эффективную площадь контакта
- Интерфейсные материалы: Тепловые соединения заполняют воздушные зазоры
- Чистота поверхности: Загрязняющие вещества могут повысить устойчивость
Тематическое исследование: Тепловая оптимизация бесштокового цилиндра
Для магнитного бесштокового цилиндра, испытывающего тепловые проблемы:
| Компонент | Оригинальный дизайн | Оптимизированный дизайн | Улучшение |
|---|---|---|---|
| Корпус цилиндра | Анодированный алюминий | Тот же материал, улучшенная отделка | 15% лучшая проводимость |
| Интерфейс подшипника | Контакт металла с металлом | Добавлена термическая смесь | 340% лучшая проводимость |
| Монтажные кронштейны | Окрашенная сталь | Голый алюминий | 280% лучшая проводимость |
| Общее термическое сопротивление | 2,8 К/ВТ | 0,7 К/ВТ | 75% уменьшение |
| Рабочая температура | 78°C | 56°C | Снижение до 22°C |
| Срок службы компонентов | 4 месяца | >12 месяцев | 3× улучшение |
Практические методы оптимизации проводимости
Исходя из моего опыта работы с сотнями пневматических систем, вот наиболее эффективные подходы к улучшению проводимости:
Оптимизация интерфейса
- Отделка поверхности: Улучшение гладкости сопрягаемых поверхностей до Ra 0,4-0,8 мкм
- Thermal Interface Materials2: Apply appropriate compounds (3-8 W/m·K)
- Fastener Torque: Ensure proper tightening for optimal contact pressure
- Cleanliness: Remove all oils and contaminants before assembly
Material Selection Strategies
- Critical Heat Paths: Use high-conductivity materials (aluminum, copper)
- Thermal Breaks: Intentionally use low-conductivity materials to isolate heat
- Composite Approaches: Combine materials for optimal performance/cost
- Anisotropic Materials: Utilize directional conductivity where appropriate
Geometric Optimization
- Heat Path Length: Minimize distance between heat sources and sinks
- Cross-Sectional Area: Maximize area perpendicular to heat flow
- Thermal Bottlenecks: Identify and eliminate constrictions in heat path
- Redundant Paths: Create multiple parallel conduction routes
Методы усиления конвекции: Какие методы обеспечивают максимальный теплообмен между воздухом и поверхностью?
Convection is often the limiting factor in pneumatic system cooling. Enhancing convective heat transfer can dramatically improve thermal management and system performance.
Convective heat transfer follows Newton’s Law of Cooling3: Q = hA(Ts-T∞), where h is the convection coefficient (W/m²·K), A is the surface area, and (Ts-T∞) is the temperature difference between the surface and fluid. Enhancement methods include increasing surface area through fins, improving fluid velocity with directed airflow, and optimizing surface characteristics to promote turbulent boundary layers.
During an energy efficiency audit at a packaging facility in Arizona, I encountered a pneumatic system operating in a 43°C ambient environment. Their rodless cylinders were overheating despite meeting all maintenance requirements. By implementing targeted convection enhancement—adding small aluminum fins and a low-power fan—we increased the convection coefficient by 450%. This reduced operating temperatures from dangerous levels to within specification without any major system modifications.
Convection Heat Transfer Fundamentals
The basic equation governing convective heat transfer is:
Q = hA(Ts-T∞)
Где:
- Q = скорость теплопередачи (Вт)
- h = Convection coefficient (W/m²·K)
- A = Surface area (m²)
- Ts = Surface temperature (K)
- T∞ = Fluid (air) temperature (K)
The convection coefficient h depends on multiple factors:
- Fluid properties (density, viscosity, thermal conductivity)
- Flow characteristics (velocity, turbulence)
- Surface geometry and orientation
- Flow regime (natural vs. forced convection)
Natural vs. Forced Convection
| Параметр | Natural Convection | Forced Convection | Implications |
|---|---|---|---|
| Typical h Value | 5-25 W/m²·K | 25-250 W/m²·K | Forced convection can be 10× more effective |
| Driving Force | Buoyancy (temperature difference) | External pressure (fans, blowers) | Forced convection is less dependent on temperature |
| Flow Pattern | Vertical flow along surfaces | Directional based on forcing mechanism | Forced flow can be optimized for specific components |
| Надежность | Passive, always present | Requires power and maintenance | Natural convection provides baseline cooling |
| Space Requirements | Requires clearance for air circulation | Requires space for air movers and ducting | Forced systems need more planning |
Convection Enhancement Techniques
Surface Area Augmentation
Increasing effective surface area through:
Fins and Extended Surfaces
– Pin fins: Omnidirectional airflow, 150-300% area increase
– Plate fins: Directional airflow, 200-500% area increase
– Corrugated surfaces: Moderate enhancement, 50-150% area increaseSurface Roughening
– Micro-texturing: 5-15% effective area increase
– Dimpled surfaces: 10-30% increase plus boundary layer effects
– Grooved patterns: 15-40% increase with directional benefits
Flow Manipulation
Improving airflow characteristics through:
Forced Air Systems
– Fans: Directional airflow, 200-600% h improvement
– Blowers: High-pressure flow, 300-800% h improvement
– Compressed air jets: Targeted cooling, 400-1000% local h improvementFlow Path Optimization
– Baffles: Direct air to critical components
– Venturi effects: Accelerate air over specific surfaces
– Vortex generators: Create turbulence for boundary layer disruption
Surface Modifications
Altering surface properties to enhance convection:
Emissivity Treatments
– Black oxide: Increases emissivity to 0.7-0.9
– Anodizing: Controlled emissivity from 0.4-0.9
– Paints and coatings: Customizable emissivity up to 0.98Wettability Control
– Hydrophilic coatings: Enhance liquid cooling
– Hydrophobic surfaces: Prevent condensation issues
– Patterned wettability: Directed condensate flow
Practical Implementation Example
For a rodless pneumatic cylinder operating in a high-temperature environment:
| Enhancement Method | Implementation | h Improvement | Temperature Reduction |
|---|---|---|---|
| Pin Fins (6mm) | Aluminum clip-on fins, 10mm spacing | 180% | 12°C |
| Directed Airflow | 80mm, 2W DC fan at 1.5 m/s | 320% | 18°C |
| Surface Treatment | Black anodizing | 40% | 3°C |
| Combined Approach | All methods integrated | 450% | 24°C |
Nusselt Number Correlation for Design Calculations
For engineering calculations, the Nusselt number4 (Nu) provides a dimensionless approach to convection:
Nu = hL/k
Где:
- L = Characteristic length
- k = Fluid thermal conductivity
For forced convection over a flat plate:
Nu = 0.664Re^(1/2)Pr^(1/3) (laminar flow)
Nu = 0.037Re^(4/5)Pr^(1/3) (turbulent flow)
Где:
- Re = Reynolds number (velocity × length × density / viscosity)
- Pr = Prandtl number (specific heat × viscosity / thermal conductivity)
These correlations allow engineers to predict convection coefficients for different configurations and optimize cooling strategies accordingly.
Модель радиационной эффективности: Когда тепловое излучение имеет значение в пневматических системах?
Radiation is often overlooked in pneumatic system thermal management, but it can account for 15-30% of total heat transfer in many applications. Understanding when and how to optimize radiative heat transfer is crucial for comprehensive thermal management.
Radiation heat transfer follows the Stefan-Boltzmann Law5: Q = εσA(T₁⁴-T₂⁴), where ε is surface emissivity, σ is the Stefan-Boltzmann constant, A is surface area, and T₁ and T₂ are absolute temperatures of the emitting surface and surroundings. Radiation efficiency in pneumatic systems depends primarily on surface emissivity, temperature differential, and view factors between components and their environment.
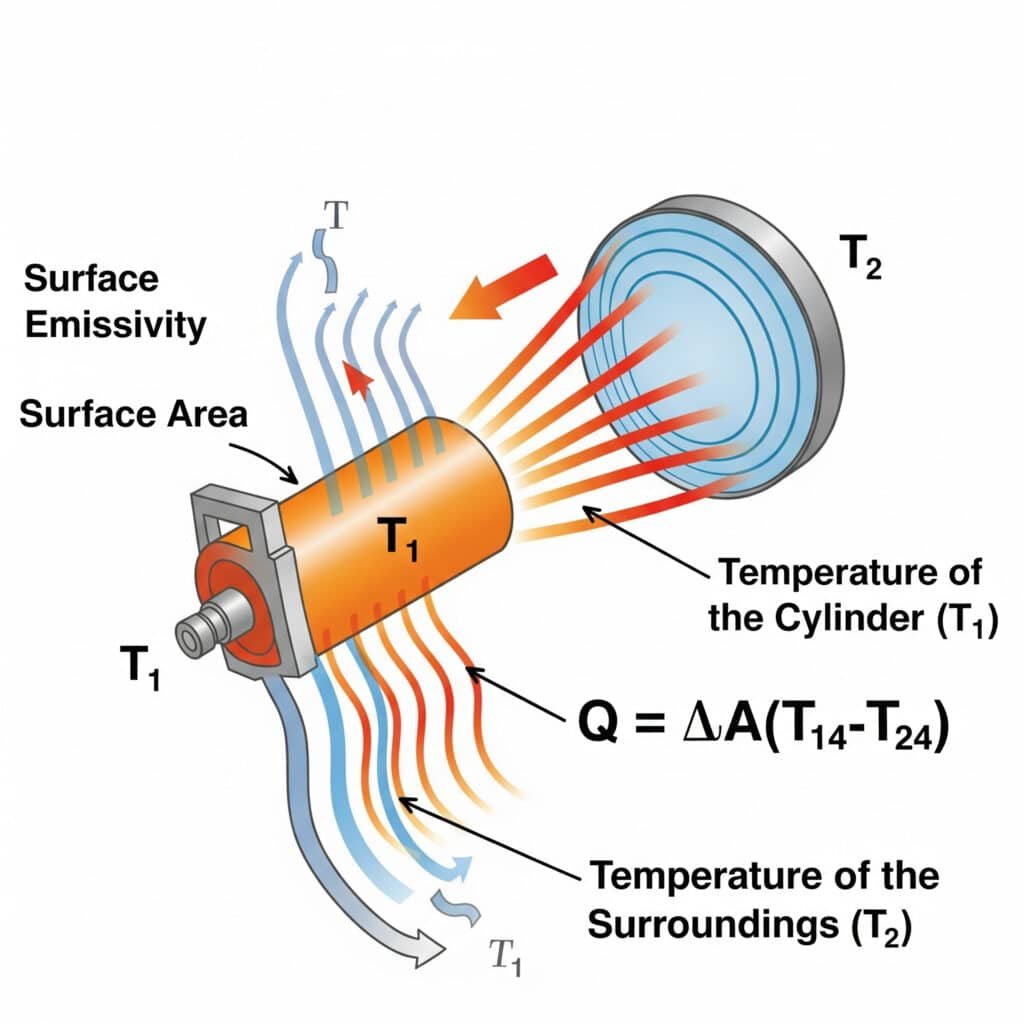
I recently helped a semiconductor equipment manufacturer in Oregon resolve overheating issues with their precision rodless cylinders. Their engineers had focused exclusively on conduction and convection but overlooked radiation. By applying a high-emissivity coating (increasing ε from 0.11 to 0.92), we enhanced radiative heat transfer by over 700%. This simple, passive solution reduced operating temperatures by 9°C without any moving parts or energy consumption—a critical requirement in their cleanroom environment.
Radiation Heat Transfer Fundamentals
The basic equation governing radiative heat transfer is:
Q = εσA(T₁⁴-T₂⁴)
Где:
- Q = скорость теплопередачи (Вт)
- ε = Emissivity (dimensionless, 0-1)
- σ = Stefan-Boltzmann constant (5.67 × 10⁻⁸ W/m²·K⁴)
- A = Surface area (m²)
- T₁ = Surface absolute temperature (K)
- T₂ = Surroundings absolute temperature (K)
Surface Emissivity Values for Common Pneumatic Materials
| Material/Surface | Emissivity (ε) | Radiation Efficiency | Enhancement Potential |
|---|---|---|---|
| Polished Aluminum | 0.04-0.06 | Very Poor | >1500% improvement possible |
| Анодированный алюминий | 0.7-0.9 | Превосходно | Already optimized |
| Stainless Steel (polished) | 0.07-0.14 | Бедный | >600% improvement possible |
| Stainless Steel (oxidized) | 0.6-0.85 | Хорошо | Moderate improvement possible |
| Steel (polished) | 0.07-0.10 | Бедный | >900% improvement possible |
| Steel (oxidized) | 0.7-0.9 | Превосходно | Already optimized |
| Painted Surfaces | 0.8-0.98 | Превосходно | Already optimized |
| PTFE (white) | 0.8-0.9 | Превосходно | Already optimized |
| Нитриловая резина | 0.86-0.94 | Превосходно | Already optimized |
View Factor Considerations
Radiation exchange depends not just on emissivity but also on geometric relationships between surfaces:
F₁₂ = Fraction of radiation leaving surface 1 that strikes surface 2
For complex geometries, view factors can be calculated using:
- Analytical solutions for simple geometries
- View factor algebra for combining known solutions
- Numerical methods for complex arrangements
- Empirical approximations for practical engineering
Temperature Dependence of Radiation
The fourth-power temperature relationship makes radiation particularly effective at higher temperatures:
| Surface Temperature | Percentage of Heat Transfer by Radiation* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Assuming natural convection conditions, ε = 0.8, 25°C ambient
Radiation Efficiency Enhancement Strategies
Based on my experience with industrial pneumatic systems, here are the most effective approaches for improving radiation heat transfer:
Surface Emissivity Modification
High-Emissivity Coatings
– Black anodizing for aluminum (ε ≈ 0.8-0.9)
– Black oxide for steel (ε ≈ 0.7-0.8)
– Specialty ceramic coatings (ε ≈ 0.9-0.98)Surface Texturing
– Micro-roughening increases effective emissivity
– Porous surfaces enhance radiative properties
– Combined emissivity/convection enhancements
Environmental Optimization
Surroundings Temperature Management
– Shielding from hot equipment/processes
– Cool walls/ceilings for better radiation exchange
– Reflective barriers to direct radiation to cooler surfacesView Factor Improvement
– Orientation to maximize exposure to cool surfaces
– Removal of blocking objects
– Reflectors to improve radiation exchange with cooler areas
Case Study: Radiation Enhancement in Precision Pneumatics
For a high-precision rodless cylinder in a cleanroom environment:
| Параметр | Оригинальный дизайн | Radiation-Enhanced Design | Улучшение |
|---|---|---|---|
| Surface Material | Polished Aluminum (ε ≈ 0.06) | Ceramic-Coated Aluminum (ε ≈ 0.94) | 1467% increase in emissivity |
| Radiation Heat Transfer | 2.1W | 32.7W | 1457% increase in radiation |
| Рабочая температура | 68°C | 59°C | 9°C reduction |
| Срок службы компонентов | 8 months | >24 months | 3× улучшение |
| Стоимость реализации | – | $175 per cylinder | 4.2 month payback |
Radiation vs. Other Heat Transfer Modes
Understanding when radiation dominates is crucial for efficient thermal management:
| Condition | Conduction Dominance | Convection Dominance | Radiation Dominance |
|---|---|---|---|
| Диапазон температур | Low to High | Low to Medium | Medium to High |
| Material Properties | High k materials | Low k, high surface area | High ε surfaces |
| Environmental Factors | Good thermal contact | Moving air, fans | Large temperature differential |
| Space Constraints | Tight packaging | Open air flow | View to cooler surroundings |
| Лучшие приложения | Component interfaces | General cooling | Hot surfaces, vacuum, still air |
Заключение
Mastering heat transfer principles—conduction coefficient calculation, convection enhancement methods, and radiation efficiency modeling—provides the foundation for effective thermal management in pneumatic systems. By applying these principles, you can reduce operating temperatures, extend component life, and improve energy efficiency while ensuring reliable operation even in challenging environments.
Вопросы и ответы о теплопередаче в пневматических системах
Каково типичное повышение температуры в пневматических цилиндрах во время работы?
При длительной работе пневматические цилиндры обычно нагреваются на 20-40°C выше окружающей среды. Это повышение происходит в результате трения между уплотнениями и стенками цилиндра, нагрева воздуха при сжатии и преобразования механической работы в тепло. Бесштоковые цилиндры часто испытывают более высокие подъемы температуры (30-50°C) из-за более сложных систем уплотнений и концентрации тепла в узле подшипник/уплотнение.
Как рабочее давление влияет на выделение тепла в пневматических системах?
Рабочее давление оказывает значительное влияние на выделение тепла, причем более высокое давление создает больше тепла за счет нескольких механизмов. Повышение рабочего давления на 1 бар обычно увеличивает тепловыделение на 8-12% из-за увеличения сил трения между уплотнениями и поверхностями, более высокого нагрева при сжатии и увеличения потерь, связанных с утечками. Эта зависимость приблизительно линейна в пределах нормального рабочего диапазона (3-10 бар).
What’s the optimal cooling approach for pneumatic components in different environments?
Оптимальный подход к охлаждению зависит от условий окружающей среды: в чистых помещениях с умеренной температурой (15-30°C) часто достаточно естественной конвекции с правильным расстоянием между компонентами. При высоких температурах (30-50°C) необходима принудительная конвекция с помощью вентиляторов или сжатого воздуха. В экстремально жарких условиях (>50°C) или при ограничении воздушного потока могут потребоваться активные методы охлаждения, такие как термоэлектрические кулеры или жидкостное охлаждение. В любом случае максимальное излучение через поверхности с высокой теплопроводностью обеспечивает дополнительное пассивное охлаждение.
Как рассчитать общую теплопередачу от пневматического компонента?
Рассчитайте общую теплопередачу, суммируя вклады каждого механизма: Qtotal = Qкондукция + Qконвекция + Qизлучение. Для теплопроводности используйте Q = kA(T₁-T₂)/L для каждого теплового пути. Для конвекции используйте Q = hA(Ts-T∞) с соответствующими коэффициентами конвекции. Для излучения используйте Q = εσA(T₁⁴-T₂⁴). В большинстве промышленных пневматических систем, работающих при температуре 30-80°C, примерное распределение составляет 20-40% кондукции, 40-70% конвекции и 10-30% излучения.
What’s the relationship between temperature and pneumatic component life?
Срок службы компонентов уменьшается экспоненциально с ростом температуры, следуя модифицированной зависимости Аррениуса. Как правило, каждые 10°C повышения рабочей температуры сокращают срок службы уплотнений и компонентов на 40-50%. Это означает, что компонент, работающий при 70°C, может прослужить лишь на треть дольше, чем тот же компонент при 50°C. Эта зависимость особенно важна для полимерных компонентов, таких как уплотнения, подшипники и прокладки, которые часто определяют интервал технического обслуживания пневматических систем.
-
Provides a foundational explanation of Fourier’s Law, the fundamental principle that describes how heat is conducted through solid materials based on their thermal conductivity and temperature gradient. ↩
-
Explains the function and types of Thermal Interface Materials (TIMs), which are used to fill microscopic air gaps between components to improve heat conduction and reduce thermal resistance. ↩
-
Details the principles of Newton’s Law of Cooling, which governs how objects cool by transferring heat to the surrounding fluid via convection, a key factor in system cooling design. ↩
-
Offers an in-depth look at the Nusselt number, a critical dimensionless quantity in fluid dynamics and heat transfer that represents the ratio of convective to conductive heat transfer across a boundary. ↩
-
Describes the Stefan-Boltzmann Law, the fundamental physical principle that quantifies the total energy radiated by a black body, which is essential for calculating heat loss from hot surfaces. ↩



