Кошмаром каждого инженера по техническому обслуживанию является неожиданный отказ оборудования. Когда машины вибрируют на своей собственной частоте, катастрофические повреждения могут произойти в течение нескольких минут. Я видел, как эта проблема стоила компаниям тысяч долларов за простой оборудования.
Вибрационный резонанс1 возникает, когда внешняя сила совпадает с собственной частотой системы, вызывая усиленные колебания, которые могут повредить оборудование. Понимание и контроль этого явления необходимы для предотвращения сбоев и продления срока службы оборудования.
Позвольте мне поделиться небольшой историей. В прошлом году клиент из Германии позвонил мне в панике. Их производственная линия остановилась из-за бесштоковый цилиндр сильно вибрировал. В чем проблема? Резонанс. К концу этой статьи вы поймете, как выявлять и предотвращать подобные проблемы в своих системах.
Оглавление
- Формула собственной частоты: Как рассчитать уязвимые точки вашей системы?
- Модель Mass-Spring: Почему этот упрощенный подход так ценен?
- Оптимизация коэффициента демпфирования: Какие эксперименты дают наилучшие результаты?
- Заключение
- Вопросы и ответы о виброрезонансе
Формула собственной частоты: Как рассчитать уязвимые точки вашей системы?
Понимание собственной частоты вашего оборудования - первый шаг к предотвращению резонансных проблем. Это критическое значение определяет, когда ваша система наиболее уязвима к проблемам вибрации.
Сайт собственная частота2 (fn) системы можно рассчитать по формуле: fn = (1/2π) × √(k/m), где k - коэффициент жесткости, а m - масса. Этот расчет позволяет определить частоту, на которой ваша система будет резонировать при возбуждении соответствующими внешними силами.
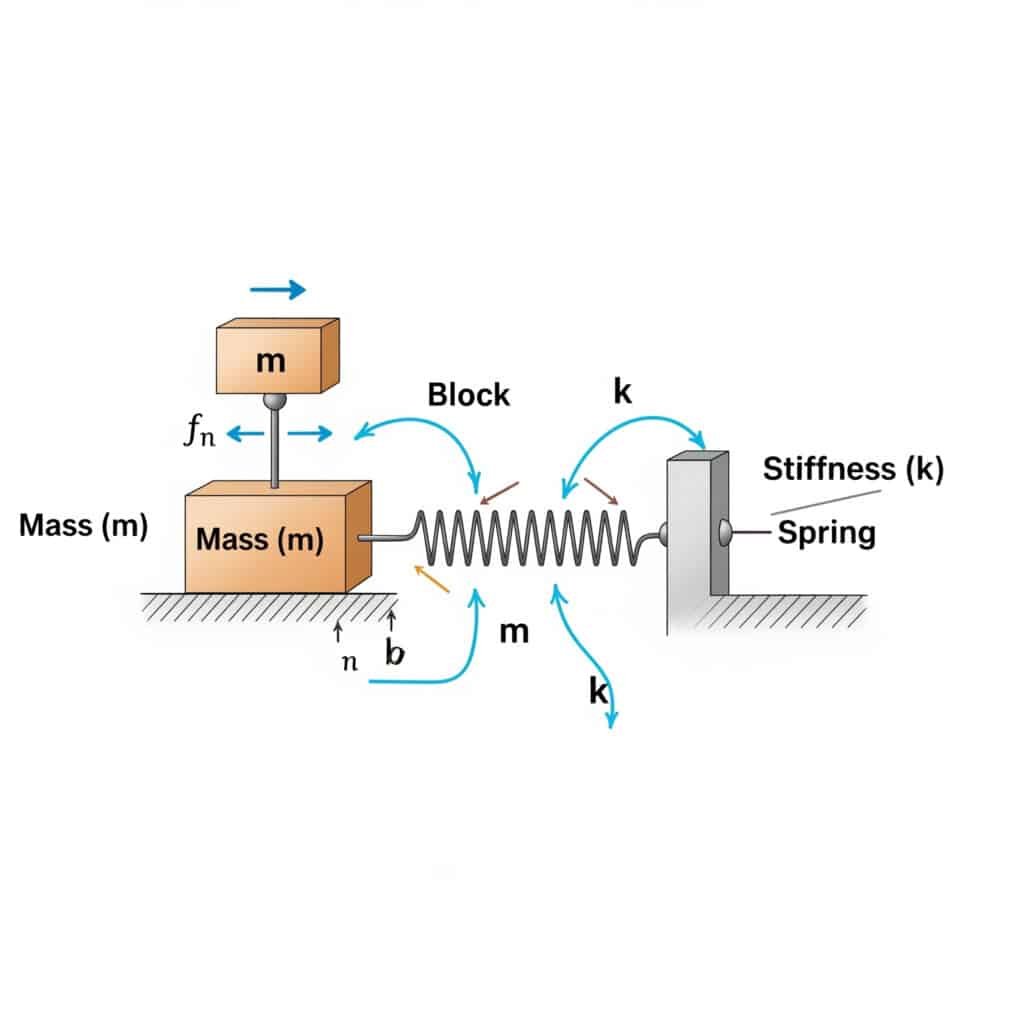
Посетив производственное предприятие в Швейцарии, я заметил, что их пневматические цилиндры без штока преждевременно выходят из строя. Специалисты по техническому обслуживанию не рассчитали собственную частоту их установки. Применив эту формулу, мы определили, что рабочая скорость была опасно близка к собственной частоте системы.
Практическое применение расчетов собственных частот
Формула собственной частоты не просто теоретическая - она имеет прямое применение в различных промышленных условиях:
- Выбор оборудования: Выбор компонентов с собственными частотами, далекими от рабочих условий
- Профилактическое обслуживание: Планирование проверок на основе профилей риска вибрации
- Устранение неполадок: Определение основной причины неожиданных вибраций
Общие значения собственных частот для промышленных компонентов
| Компонент | Типичный диапазон собственных частот (Гц) |
|---|---|
| Бесштоковые цилиндры | 10-50 Гц |
| Монтажные кронштейны | 20-100 Гц |
| Вспомогательные структуры | 5-30 Гц |
| Регулирующие клапаны | 40-200 Гц |
Критические факторы, влияющие на собственную частоту
Расчет собственной частоты кажется простым, но несколько факторов могут усложнить его применение в реальных условиях:
- Неравномерное распределение массы: Большинство промышленных компонентов не имеют идеально распределенной массы
- Переменная жесткость: Компоненты могут иметь различную жесткость в разных направлениях
- Точки подключения: Способ монтажа компонентов существенно влияет на их вибрационные характеристики
- Температурные эффекты: Свойства массы и жесткости могут изменяться с температурой
Модель Mass-Spring: Почему этот упрощенный подход так ценен?
Модель "масса-пружина" обеспечивает интуитивно понятную основу для понимания сложных вибрационных систем. Она сводит сложные механизмы к базовым элементам, которые инженеры могут легко анализировать.
Сайт пружинно-массовая модель3 упрощает анализ вибраций, представляя механические системы как дискретные массы, соединенные пружинами. Такой подход позволяет инженерам прогнозировать поведение системы, выявлять потенциальные резонансные проблемы и разрабатывать эффективные решения без сложной математики.
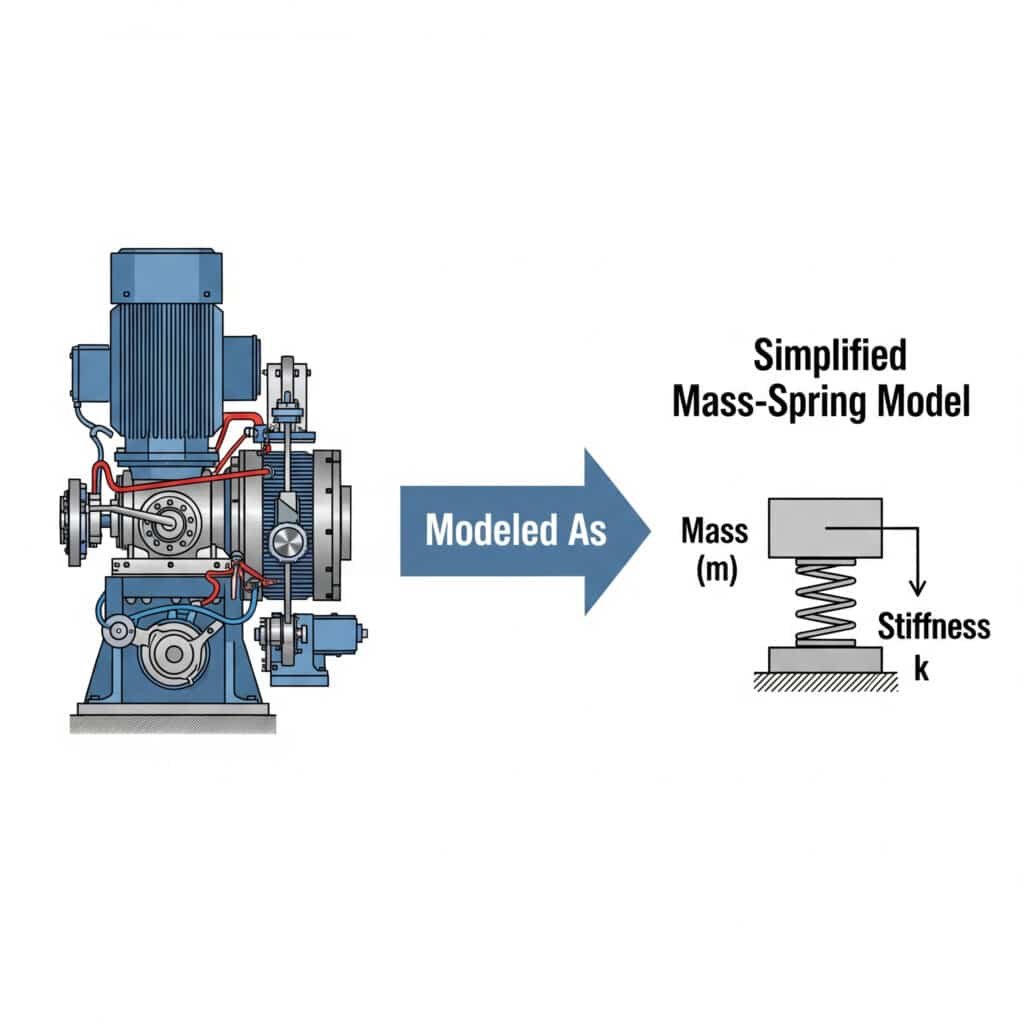
Я помню, как работал с производителем автомобильных деталей в Мичигане, который не мог понять, почему его направляющие бесштоковые цилиндры выходят из строя. Смоделировав их систему как простую систему "масса-пружина", мы определили, что монтажные кронштейны действуют как непредусмотренные пружины, создавая условия резонанса.
Преобразование реальных систем в модели Масс-Спринга
Чтобы применить этот подход к вашему оборудованию:
- Определите основные массы: Определите, какие компоненты вносят значительный вес
- Найдите пружинные элементы: Найдите компоненты, которые накапливают и отдают энергию (настоящие пружины, гибкие крепления и т.д.).
- Соединения на карте: Зафиксируйте взаимодействие масс и пружин
- Упростите: Объедините похожие элементы, чтобы создать управляемую модель
Типы пружинных систем
| Тип системы | Описание | Общие приложения |
|---|---|---|
| Одиночная DOF | Одна масса с одной пружиной | Простые пневматические цилиндры |
| Multi-DOF | Несколько масс с несколькими пружинами | Сложное оборудование с многочисленными компонентами |
| Непрерывный | Бесконечная DOF (требует другого анализа) | Балки, плиты и оболочки |
Расширенные возможности моделирования
Несмотря на ценность базовой модели "масса-пружина", несколько усовершенствований делают ее более реалистичной:
- Добавление демпферов: В реальных системах всегда есть диссипация энергии
- Учет нелинейности: Пружины не всегда следуют Закон Гука4 идеально
- Учет принудительной вибрации: Внешние силы изменяют поведение системы
- Включение эффектов сопряжения: Движение в одном направлении может влиять на другие направления
Оптимизация коэффициента демпфирования: Какие эксперименты дают наилучшие результаты?
Демпфирование - лучшая защита от проблем с резонансом. Нахождение оптимального соотношения демпфирования путем экспериментов может значительно улучшить производительность и надежность системы.
Коэффициент демпфирования5 Эксперименты по оптимизации включают в себя систематическое тестирование различных конфигураций демпфирования для поиска идеального баланса между контролем вибраций и отзывчивостью системы. Оптимальный коэффициент демпфирования обычно находится в диапазоне от 0,2 до 0,7, обеспечивая достаточное подавление вибраций без чрезмерных потерь энергии.
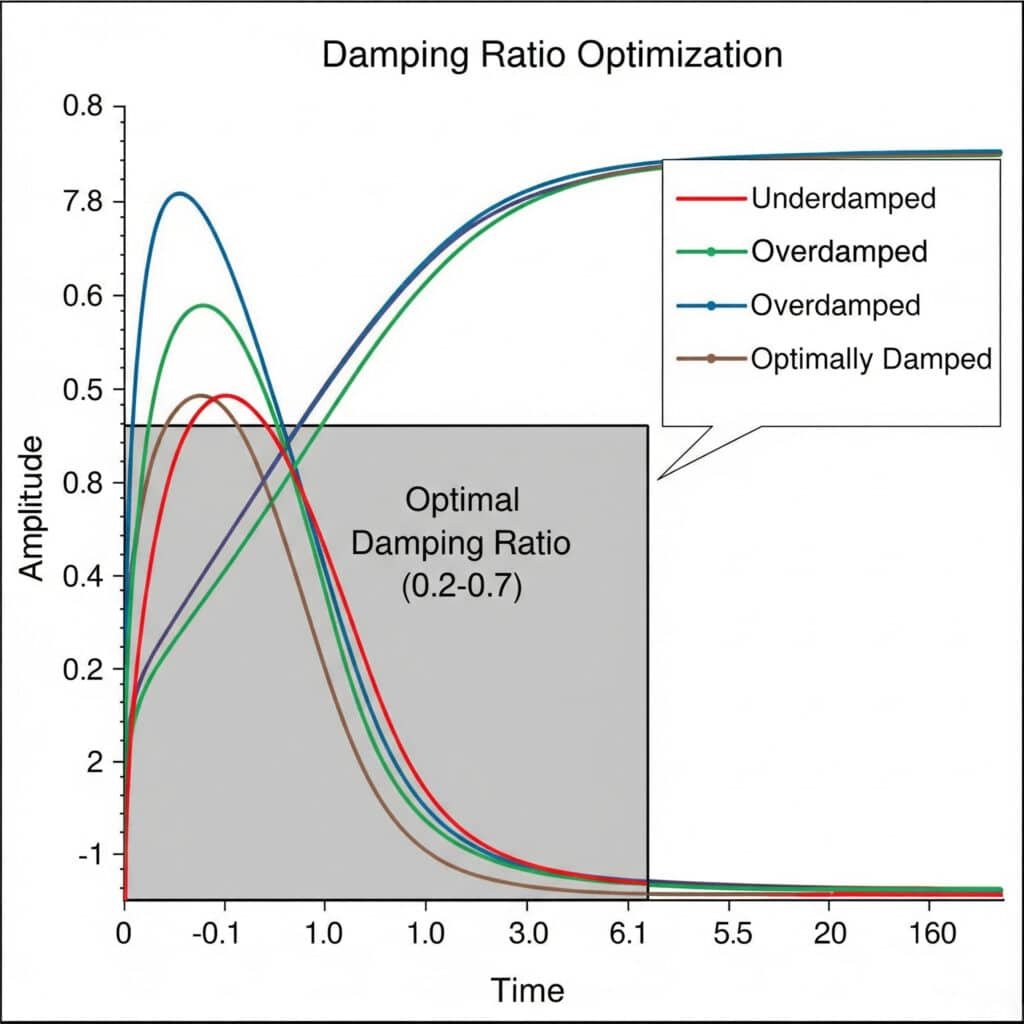
В прошлом месяце я помог производителю оборудования для пищевой промышленности во Франции решить постоянные проблемы с вибрацией в их магнитных бесштоковых цилиндрах. Проведя серию экспериментов с коэффициентом демпфирования, мы обнаружили, что в их оригинальной конструкции коэффициент демпфирования составлял всего 0,05 - слишком мало для предотвращения резонансных проблем.
Экспериментальная установка для испытания коэффициента демпфирования
Провести эксперименты по оптимизации эффективного демпфирования:
- Базовое измерение: Запись отклика системы без дополнительного демпфирования
- Инкрементное тестирование: Добавление демпфирующих элементов с контролируемым шагом
- Измерение реакции: Измерение амплитуды, времени установления и частотной характеристики
- Анализ данных: Рассчитайте коэффициент демпфирования для каждой конфигурации
- Валидация: Проверьте производительность в реальных условиях эксплуатации
Сравнение технологий демпфирования
| Технология демпфирования | Преимущества | Ограничения | Типовые применения |
|---|---|---|---|
| Вязкие демпферы | Предсказуемая производительность, стабильная температура | Требуют обслуживания, возможны протечки | Тяжелые машины, прецизионное оборудование |
| Фрикционные демпферы | Простой дизайн, экономичность | Износ с течением времени, нелинейное поведение | Структурные опоры, основные механизмы |
| Демпфирование материала | Отсутствие движущихся частей, компактность | Ограниченный диапазон регулировки | Прецизионные приборы, виброизоляция |
| Активное демпфирование | Адаптируется к меняющимся условиям | Сложный, требует питания | Критические приложения, оборудование с переменной скоростью |
Оптимизация демпфирования для различных условий эксплуатации
Идеальный коэффициент демпфирования не является универсальным - он зависит от конкретного применения:
- Высокоскоростные операции: Более низкие коэффициенты демпфирования (0,1-0,3) сохраняют отзывчивость
- Прецизионные приложения: Более высокие коэффициенты демпфирования (0,5-0,7) обеспечивают стабильность
- Системы с переменной нагрузкой: Может потребоваться адаптивное демпфирование
- Чувствительные к температуре среды: Рассмотрите демпфирующие материалы со стабильными свойствами
Тематическое исследование: Оптимизация демпфирования бесштокового цилиндра
При оптимизации цилиндра двойного действия без штока для упаковочной машины мы испытали пять различных конфигураций демпфирования:
- Стандартные торцевые подушки: Коэффициент демпфирования = 0,12
- Удлиненные подушки: Коэффициент демпфирования = 0,25
- Внешние амортизаторы: Коэффициент демпфирования = 0,41
- Составные монтажные кронштейны: Коэффициент демпфирования = 0,38
- Комбинированный подход (3+4): Коэффициент демпфирования = 0,53
Комбинированный подход обеспечил наилучшую производительность, снизив амплитуду вибрации на 78% при сохранении приемлемого времени отклика.
Заключение
Понимание резонанса вибрации с помощью расчетов собственных частот, моделирования масс и пружин и оптимизации коэффициента демпфирования имеет решающее значение для предотвращения отказов оборудования. Применяя эти принципы, вы сможете продлить срок службы оборудования, сократить время простоя и повысить общую производительность системы.
Вопросы и ответы о виброрезонансе
Что такое виброрезонанс в промышленном оборудовании?
Вибрационный резонанс возникает, когда внешняя сила совпадает с собственной частотой системы, вызывая усиленные колебания. В промышленном оборудовании это явление может привести к чрезмерным перемещениям, усталости компонентов и катастрофическим отказам, если не управлять им должным образом.
Как определить, что моя система находится в резонансе?
Ищите такие симптомы, как необъяснимое повышение уровня шума, заметная вибрация на определенных скоростях, преждевременный отказ компонентов и снижение производительности при постоянных рабочих режимах. Инструменты анализа вибрации могут подтвердить наличие резонанса.
В чем разница между принудительной вибрацией и резонансом?
Вынужденная вибрация возникает всякий раз, когда на систему действует внешняя сила, а резонанс - это особое состояние, когда частота вынужденной вибрации совпадает с собственной частотой системы, что приводит к усилению отклика. Все резонансы связаны с вынужденной вибрацией, но не все вынужденные вибрации вызывают резонанс.
Как конструкция бесштокового пневматического цилиндра влияет на его вибрационные характеристики?
Конструкция бесштоковых пневматических цилиндров с их подвижной кареткой, внутренней системой уплотнений и направляющими механизмами создает уникальные проблемы, связанные с вибрацией. Удлиненный профиль действует как балка, которая может изгибаться, масса каретки создает инерционные силы, а уплотнительные ленты могут создавать переменное трение.
Какие простые модификации могут уменьшить резонанс в существующем оборудовании?
Для существующего оборудования, испытывающего проблемы с резонансом, рассмотрите возможность добавления массы для изменения собственной частоты, установки внешних демпферов или амортизаторов, изменения методов монтажа для обеспечения виброизоляции или регулировки рабочей скорости, чтобы избежать резонансных частот.
-
Дается фундаментальное объяснение механического резонанса, часто с наглядными примерами, демонстрирующими, как небольшая периодическая сила может вызвать колебания большой амплитуды в системе. ↩
-
Предлагает подробное рассмотрение физики собственной частоты - определенной частоты, на которой система склонна колебаться в отсутствие какой-либо движущей или демпфирующей силы. ↩
-
Объясняет принципы модели "масса-пружина" - фундаментальной идеализации в физике и технике, используемой для анализа сложных систем, демонстрирующих простое гармоническое движение. ↩
-
Подробнее Закон Гука - принцип физики, согласно которому сила, необходимая для растяжения или сжатия пружины на некоторое расстояние, прямо пропорциональна этому расстоянию. ↩
-
Описывает коэффициент демпфирования, безразмерную меру, которая определяет, как затухают колебания в системе после возмущения, что очень важно для борьбы с резонансом. ↩


