Prestoje vo výrobe stoja spoločnosti milióny ročne. Pneumatické valce poháňajú 80% systémov priemyselnej automatizácie. Napriek tomu mnohí inžinieri úplne nerozumejú fyzikálnym základom, vďaka ktorým sú tieto systémy také spoľahlivé a efektívne.
Teória pneumatických valcov je založená na Pascalovom zákone, podľa ktorého tlak stlačeného vzduchu pôsobí v uzavretej komore rovnako vo všetkých smeroch a prostredníctvom tlakových rozdielov premieňa pneumatickú energiu na mechanický lineárny alebo rotačný pohyb.
Pred dvoma rokmi som spolupracoval s britským inžinierom Jamesom Thompsonom z Manchestru, ktorého výrobná linka neustále zlyhávala. Jeho tím nechápal, prečo ich pneumatický systém prerušovane stráca výkon. Po vysvetlení základnej teórie sme identifikovali problémy s poklesom tlaku, ktoré jeho spoločnosti ušetrili 200 000 libier za stratu výroby.
Obsah
- Aké sú základné fyzikálne princípy pneumatických valcov?
- Ako tlakové rozdiely vytvárajú pohyb v pneumatických systémoch?
- Aké sú kľúčové komponenty, vďaka ktorým funguje pneumatická teória?
- Ako sa tieto princípy uplatňujú pri rôznych typoch pneumatických valcov?
- Aké faktory ovplyvňujú teóriu výkonu pneumatických valcov?
- Ako sa dá porovnať teória pneumatiky s hydraulickými a elektrickými systémami?
- Záver
- Často kladené otázky o teórii pneumatických valcov
Aké sú základné fyzikálne princípy pneumatických valcov?
Pneumatické valce fungujú na základných fyzikálnych princípoch, ktoré poháňajú priemyselnú automatizáciu už viac ako storočie. Pochopenie týchto základov pomáha inžinierom navrhovať lepšie systémy a efektívne riešiť problémy.
Pneumatické valce pracujú na základe Pascalovho zákona, Boylovho zákona a Newtonove zákony pohybu1, ktoré premieňajú energiu stlačeného vzduchu na mechanickú silu prostredníctvom tlakových rozdielov na povrchu piestu.
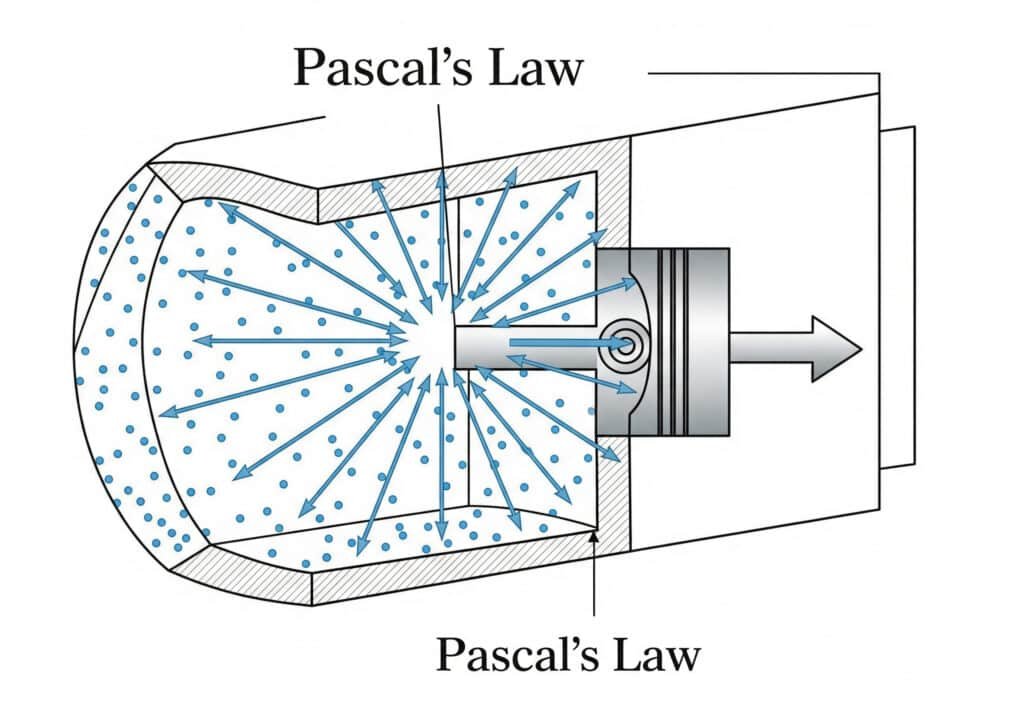
Aplikácia Pascalovho zákona
Pascalov zákon hovorí, že tlak pôsobiaci na uzavretú kvapalinu sa prenáša rovnako vo všetkých smeroch. V pneumatických valcoch to znamená, že tlak stlačeného vzduchu pôsobí rovnomerne na celú plochu piestu.
Základná rovnica sily je: Sila = tlak × plocha
Pre valec s priemerom 4 palce pri tlaku 100 PSI:
- Plocha piestu = π × (2)² = 12,57 palca štvorcového
- Výstupná sila = 100 PSI × 12,57 = 1 257 libier
Boyleov zákon a kompresia vzduchu
Boyleov zákon vysvetľuje, ako sa mení objem vzduchu s tlakom pri konštantnej teplote. Tento princíp určuje, ako stlačený vzduch ukladá energiu a uvoľňuje ju počas prevádzky valca.
Keď sa vzduch stlačí z atmosférického tlaku (14,7 PSI) na 114,7 PSI (absolútny tlak), jeho objem sa zmenší približne o 87%. V tomto stlačenom vzduchu sa ukladá potenciálna energia, ktorá sa počas rozťahovania valca mení na kinetickú energiu.
Newtonove zákony v pneumatickom pohybe
Druhý Newtonov zákon (F = ma) určuje zrýchlenie a rýchlosť valca. Vyššie tlakové rozdiely vytvárajú väčšie sily, čo vedie k rýchlejšiemu zrýchleniu, kým trenie a odpor zaťaženia nevyvážia hnaciu silu.
Kľúčové fyzikálne vzťahy:
| Právo | Aplikácia | Vzorec | Vplyv na výkon |
|---|---|---|---|
| Pascalov zákon | Generovanie sily | F = P × A | Určuje maximálnu silu |
| Boyleov zákon | Stlačenie vzduchu | P₁V₁ = P₂V₂ | Ovplyvňuje ukladanie energie |
| Newtonova 2. | Dynamika pohybu | F = ma | Ovládanie rýchlosti/zrýchlenia |
| Zachovanie energie | Účinnosť | Ein = Eout + Straty | Určuje účinnosť systému |
Ako tlakové rozdiely vytvárajú pohyb v pneumatických systémoch?
Tlakové rozdiely sú hnacou silou všetkých pohybov pneumatických valcov. Čím väčší je tlakový rozdiel na pieste, tým väčšiu silu a rýchlosť valec vytvára.
K pohybu dochádza, keď stlačený vzduch vstupuje do jednej komory valca, zatiaľ čo opačná komora odvádza vzduch do atmosféry, čím vzniká tlakový rozdiel, ktorý poháňa pohyb piestu pozdĺž otvoru valca.
Teória jednočinného valca
Jednočinné valce používajú stlačený vzduch len v jednom smere. Pružina alebo gravitácia vracia piest do pôvodnej polohy po uvoľnení tlaku vzduchu.
Pri výpočte efektívnej sily sa musí zohľadniť odpor pružiny:
Čistá sila = (tlak × plocha) - sila pružiny - trenie
Sila pružiny sa zvyčajne pohybuje v rozmedzí 10-30% maximálnej sily valca, čo znižuje celkový výkon, ale zabezpečuje spoľahlivý spätný pohyb.
Teória dvojčinného valca
Dvojčinné valce používajú stlačený vzduch na vysúvanie aj sťahovanie. Táto konštrukcia poskytuje maximálnu silu v oboch smeroch a presné ovládanie polohy piestu.
Výpočty sily pre dvojčinné valce:
Rozširujúca sila: F = P × (plná plocha piestu)
Sila vtiahnutia: F = P × (plná plocha piestu - plocha tyče)
Zmenšenie plochy tyče znamená, že sila na vťahovanie je vždy menšia ako sila na vysúvanie. Pre 4-palcový valec s 1-palcovou tyčou:
- Oblasť rozšírenia: 12,57 palca štvorcového
- Oblasť stiahnutia: 12,57 - 0,785 = 11,785 štvorcových palcov
- Rozdiel síl: približne o 6% menej pri sťahovaní
Teória poklesu tlaku
Poklesy tlaku2 sa vyskytujú v pneumatických systémoch v dôsledku trenia, armatúr a obmedzení ventilov. Tieto straty priamo znižujú výkon valcov a musia sa zohľadniť pri návrhu systému.
Bežné zdroje poklesu tlaku:
- Vzduchové vedenia: 1-3 PSI na 100 stôp
- Príslušenstvo: 0,5-2 PSI za kus
- Ventily: 2-8 PSI v závislosti od konštrukcie
- Filtre: 1-5 PSI, keď je čistý
Aké sú kľúčové komponenty, vďaka ktorým funguje pneumatická teória?
Teória pneumatických valcov sa zakladá na presne navrhnutých komponentoch, ktoré spolu spolupracujú. Každý komponent plní špecifickú funkciu pri premene energie stlačeného vzduchu na mechanický pohyb.
Medzi základné komponenty patrí valec, piest, tyč, tesnenia a koncové uzávery, ktoré sú navrhnuté tak, aby zadržiavali tlak, usmerňovali pohyb a účinne prenášali silu.
Inžinierstvo valcov
Hlaveň valca musí odolávať vnútornému tlaku pri zachovaní presných rozmerov otvoru. Väčšina priemyselných valcov používa bezšvové oceľové alebo hliníkové rúrky s brúsené vnútorné povrchy3.
Špecifikácie hlavne:
| Materiál | Hodnota tlaku | Povrchová úprava | Typické aplikácie |
|---|---|---|---|
| Hliník | Do 250 PSI | 16-32 Ra | Ľahké, potravinárske |
| Oceľ | Až do 500 PSI | 8-16 Ra | Vysokotlakové zariadenia pre vysoké zaťaženie |
| Nerezová oceľ | Do 300 PSI | 8-32 Ra | Korózne prostredia |
Teória konštrukcie piestov
Piesty prenášajú tlakovú silu na tyč a zároveň utesňujú dve vzduchové komory. Konštrukcia piestu ovplyvňuje účinnosť valca, rýchlosť a životnosť.
Moderné piesty používajú viacero tesniacich prvkov:
- Primárna pečať: Zabraňuje úniku vzduchu medzi komorami
- Nosiť krúžky: Vedenie pohybu piestu a zabránenie kontaktu s kovom
- Sekundárne tesnenia: Záložné tesnenie pre kritické aplikácie
Teória tesniaceho systému
Tesnenia majú rozhodujúci význam pre udržanie tlakových rozdielov. Zlyhanie tesnenia je najčastejšou príčinou problémov s pneumatickými valcami v priemyselných aplikáciách.
Faktory výkonu tesnenia:
- Výber materiálu: Musí odolávať prenikaniu vzduchu a opotrebovaniu
- Drážkový dizajn: Správne rozmery zabraňujú vytláčaniu tesnenia
- Povrchová úprava: Hladký povrch znižuje opotrebovanie tesnenia
- Prevádzkový tlak: Vyššie tlaky si vyžadujú špeciálne konštrukcie tesnení
Ako sa tieto princípy uplatňujú pri rôznych typoch pneumatických valcov?
Rôzne konštrukcie pneumatických valcov používajú rovnakú základnú teóriu, ale optimalizujú výkon pre konkrétne aplikácie. Pochopenie týchto variácií pomáha inžinierom pri výbere vhodných riešení.
Rôzne typy valcov modifikujú základnú pneumatickú teóriu prostredníctvom špecializovaných konštrukcií, ako sú bezprúdové valce, rotačné pohony a viacpolohové valce, pričom každý z nich optimalizuje silu, rýchlosť alebo charakteristiky pohybu.
Pneumatický valec bez tyče
Valce bez tyčí4 Teória
eliminuje tradičnú piestnu tyč, čo umožňuje dlhšie zdvihy v kompaktných priestoroch. Na prenos pohybu mimo valca používajú magnetické spojky alebo káblové systémy.
Konštrukcia magnetickej spojky:
Vnútorný piest obsahuje permanentné magnety, ktoré sa spájajú s vonkajším vozíkom cez stenu valca. Táto konštrukcia zabraňuje úniku vzduchu a zároveň prenáša plnú silu piestu.
Účinnosť prenosu sily: 95-98% so správnou magnetickou väzbou
Maximálny zdvih: Obmedzené len dĺžkou valca, až do 20+ stôp
Schopnosť rýchlosti: Až 60 palcov za sekundu v závislosti od zaťaženia
Teória rotačného pohonu
Rotačné pneumatické pohony5 premieňať lineárny pohyb piestu na rotačný pohyb prostredníctvom prevodových mechanizmov alebo lopatkových konštrukcií. Tieto systémy využívajú pneumatickú teóriu na vytvorenie presného uhlového polohovania.
Rotačné pohony lopatkového typu:
Stlačený vzduch pôsobí na lopatky vo valcovej komore a vytvára rotačný krútiaci moment. Výpočet krútiaceho momentu je nasledovný: Krútiaci moment = tlak × plocha lopatiek × polomer
Teória viacpolohových valcov
Viacpolohové valce využívajú viacero vzduchových komôr na vytvorenie medzipoloh zastavenia. Táto konštrukcia využíva pneumatickú teóriu s komplexnými ventilovými systémami na presné riadenie polohy.
Medzi bežné konfigurácie patria:
- Trojpolohová: Dve medzizastávky a plné vysunutie
- Päťpolohový: Štyri medzizastávky a plný zdvih
- Variabilná poloha: Nekonečné polohovanie so servoventilom
Aké faktory ovplyvňujú teóriu výkonu pneumatických valcov?
Na to, ako dobre sa teória pneumatiky premieta do skutočného výkonu, má vplyv viacero faktorov. Pochopenie týchto premenných pomáha inžinierom optimalizovať návrh systému a odstraňovať problémy.
Medzi kľúčové faktory výkonu patria kvalita vzduchu, teplotné zmeny, charakteristiky zaťaženia, spôsoby montáže a stabilita tlaku v systéme, ktoré môžu významne ovplyvniť teoretický výkon.
Vplyv kvality ovzdušia na teóriu
Kvalita stlačeného vzduchu priamo ovplyvňuje výkon a životnosť pneumatických valcov. Znečistený vzduch spôsobuje opotrebovanie tesnenia, koróziu a zníženú účinnosť.
Normy kvality ovzdušia:
| Kontaminant | Maximálna úroveň | Vplyv na výkon |
|---|---|---|
| Vlhkosť | Rosný bod -40°F | Zabraňuje korózii a zamrznutiu |
| Olej | 1 mg/m³ | Znižuje degradáciu tesnenia |
| Častice | 5 mikrónov | Zabraňuje opotrebovaniu a lepeniu |
Vplyv teploty na pneumatickú teóriu
Zmeny teploty ovplyvňujú hustotu vzduchu, tlak a rozmery komponentov. Tieto zmeny môžu výrazne ovplyvniť výkonnosť valcov v extrémnych prostrediach.
Vzorec kompenzácie teploty: P₂ = P₁ × (T₂/T₁)
Pri každom zvýšení teploty o 100 °F sa tlak vzduchu zvýši približne o 20%, ak objem zostane konštantný. To ovplyvňuje výkon sily a musí sa zohľadniť pri návrhu systému.
Charakteristiky zaťaženia a dynamické sily
Statické a dynamické zaťaženie ovplyvňuje výkonnosť valcov odlišne. Dynamické zaťaženie vytvára dodatočné sily, ktoré je potrebné prekonať počas fáz zrýchľovania a spomaľovania.
Dynamická analýza sily:
- Sila zrýchlenia: F = ma (hmotnosť × zrýchlenie)
- Trecia sila: Zvyčajne 10-20% aplikovaného zaťaženia
- Zotrvačné sily: Významné pri vysokých rýchlostiach alebo pri veľkom zaťažení
Nedávno som pomáhal americkému výrobcovi Robertovi Chenovi v Detroite optimalizovať jeho pneumatický systém pre ťažké automobilové diely. Analýzou dynamických síl sme skrátili čas cyklu o 30% a zároveň zlepšili presnosť polohovania.
Stabilita tlaku v systéme
Kolísanie tlaku ovplyvňuje konzistenciu výkonu valcov. Správna úprava a skladovanie vzduchu pomáhajú udržiavať stabilné prevádzkové podmienky.
Požiadavky na stabilitu tlaku:
- Zmena tlaku: Pre konzistentný výkon by nemal prekročiť ±5%
- Veľkosť nádrže prijímača: 5-10 galónov na CFM spotreby vzduchu
- Regulácia tlaku: V rozmedzí ±1 PSI pre presné aplikácie
Ako sa dá porovnať teória pneumatiky s hydraulickými a elektrickými systémami?
Pneumatická teória ponúka v porovnaní s inými spôsobmi prenosu energie výrazné výhody a obmedzenia. Pochopenie týchto rozdielov pomáha inžinierom pri výbere optimálnych riešení pre konkrétne aplikácie.
Pneumatické systémy poskytujú rýchlu odozvu, jednoduché ovládanie a čistú prevádzku, ale v porovnaní s hydraulickými a elektrickými alternatívami majú nižšiu hustotu sily a menej presné polohovanie.
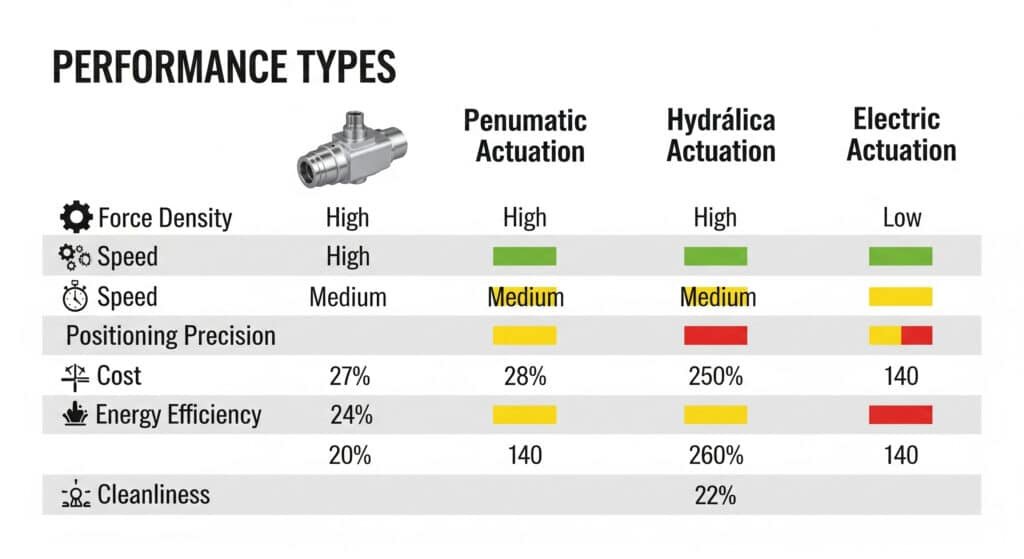
Teoretické porovnanie výkonu
| Charakteristika | Pneumatické | Hydraulika | Elektrické |
|---|---|---|---|
| Hustota výkonu | 15-25 HP/lb | 50-100 HP/lb | 5-15 HP/lb |
| Čas odozvy | 10-50 ms | 5-20 ms | 50-200 ms |
| Presnosť polohovania | ±0,1 palca | ±0,01 palca | ±0,001 palca |
| Prevádzkový tlak | 80-150 PSI | 1000-5000 PSI | N/A (napätie) |
| Účinnosť | 20-30% | 40-60% | 80-95% |
| Frekvencia údržby | Nízka | Vysoká | Stredné |
Teória účinnosti premeny energie
Pneumatické systémy majú prirodzené obmedzenia účinnosti v dôsledku stlačenia vzduchu a tvorby tepla. Teoretická maximálna účinnosť je približne 37% pri izotermickej kompresii, ale reálne systémy dosahujú 20-30%.
Zdroje straty energie:
- Kompresné teplo: 60-70% vstupnej energie
- Poklesy tlaku: 5-15% systémového tlaku
- Únik: 2-10% spotreby vzduchu
- Škrtenie strát: Variabilné v závislosti od spôsobu kontroly
Rozdiely v teórii riadenia
Teória pneumatického riadenia sa výrazne líši od hydraulických a elektrických systémov kvôli stlačiteľnosti vzduchu. Táto vlastnosť poskytuje prirodzené tlmenie, ale sťažuje presné polohovanie.
Kontrolné charakteristiky:
- Prirodzený súlad: Stlačiteľnosť vzduchu zabezpečuje tlmenie nárazov
- Regulácia rýchlosti: Dosahuje sa skôr obmedzením prietoku ako zmenou tlaku
- Kontrola sily: Ťažké vzhľadom na zložitosť vzťahu tlak/prúdenie
- Spätná väzba na pozíciu: Vyžaduje externé senzory na presné ovládanie
Záver
Teória pneumatických valcov spája základné fyzikálne princípy s praktickým inžinierstvom s cieľom vytvoriť spoľahlivé a účinné systémy prenosu energie pre nespočetné množstvo priemyselných aplikácií na celom svete.
Často kladené otázky o teórii pneumatických valcov
Aká je základná teória pneumatických valcov?
Pneumatické valce fungujú na základe Pascalovho zákona, podľa ktorého tlak stlačeného vzduchu pôsobí v uzavretej komore rovnako vo všetkých smeroch a vytvára silu, keď tlakové rozdiely posúvajú piesty cez otvory valca.
Ako vypočítate silu pneumatického valca?
Sila sa rovná tlaku krát plocha piestu (F = P × A). Valec s priemerom 4 palce pri tlaku 100 PSI vytvára približne 1 257 libier sily po odpočítaní trenia a iných strát.
Prečo sú pneumatické valce menej účinné ako hydraulické systémy?
Stlačiteľnosť vzduchu spôsobuje straty energie počas kompresných a expanzných cyklov, čo obmedzuje účinnosť pneumatických systémov na 20-30% v porovnaní s hydraulickými systémami dosahujúcimi účinnosť 40-60%.
Aké faktory ovplyvňujú rýchlosť pneumatických valcov?
Otáčky závisia od prietoku vzduchu, objemu valca, hmotnosti nákladu a tlakového rozdielu. Vyššie prietoky a tlaky zvyšujú rýchlosť, zatiaľ čo ťažšie zaťaženie znižuje zrýchlenie.
Ako teplota ovplyvňuje výkon pneumatických valcov?
Zmeny teploty ovplyvňujú hustotu a tlak vzduchu. Každé zvýšenie o 100 °C zvyšuje tlak vzduchu približne o 20%, čo priamo ovplyvňuje výkon a výkonnosť systému.
Aký je rozdiel medzi teóriou jednočinného a dvojčinného valca?
Jednočinné valce používajú stlačený vzduch len v jednom smere s vratnou pružinou, zatiaľ čo dvojčinné valce používajú tlak vzduchu na vysúvanie aj zasúvanie.
-
Poskytuje podrobný prehľad troch Newtonových pohybových zákonov, ktoré sú základnými princípmi klasickej mechaniky opisujúcimi vzťah medzi telesom a silami, ktoré naň pôsobia, a jeho pohyb ako reakciu na tieto sily. ↩
-
Podrobne opisuje príčiny poklesu tlaku v pneumatických systémoch vrátane trenia v potrubí a strát spôsobených armatúrami, ventilmi a filtrami a vysvetľuje, ako sa znižuje dostupná energia v mieste použitia. ↩
-
Vysvetľuje proces honovania, proces abrazívneho obrábania, pri ktorom sa na obrobku vytvára presný povrch drhnutím brúsnym kameňom, často používaným na vytvorenie špecifického krížového šrafovania na otvoroch valcov na zachytávanie oleja. ↩
-
Opisuje rôzne konštrukcie bezprúdových valcov, ako sú magneticky spriahnuté a mechanicky spriahnuté (pásové) typy, a vysvetľuje ich príslušné výhody, ako napríklad poskytovanie dlhých zdvihov v kompaktnom priestore. ↩
-
Vysvetľuje rôzne mechanizmy, ako sú ozubené kolesá alebo lopatkové konštrukcie, ktoré pneumatické rotačné pohony používajú na premenu lineárnej sily zo stlačeného vzduchu na rotačný pohyb alebo krútiaci moment. ↩




