
Máte problém predpovedať skutočný výkon vášho pneumatického valca? Mnohí inžinieri nesprávne odhadujú silové výkony a požiadavky na tlak, čo vedie k poruchám systému a nákladným prestojom. Existuje však jednoduchý spôsob, ako tieto výpočty zvládnuť.
Pneumatické valce fungujú na základe základných fyzikálnych princípov, predovšetkým Pascalov zákon1, podľa ktorej sa tlak pôsobiaci na uzavretú kvapalinu prenáša rovnako vo všetkých smeroch. To nám umožňuje vypočítať silu vo valci vynásobením tlaku efektívnou plochou piestu, pričom prietoky a jednotky tlaku si vyžadujú presné prepočty na presný návrh systému.
Viac ako desať rokov som pomáhal zákazníkom optimalizovať ich pneumatické systémy a videl som, ako môže pochopenie týchto základných princípov zmeniť spoľahlivosť systému. Podelím sa s vami o praktické poznatky, ktoré vám pomôžu vyhnúť sa bežným chybám, s ktorými sa stretávam každý deň.
Obsah
- Ako Pascalov zákon určuje výkon sily vo valci?
- Aký je vzťah medzi prietokom vzduchu a tlakom vo valcoch?
- Prečo je pre návrh systému dôležité porozumieť prepočtu jednotiek tlaku?
- Záver
- Často kladené otázky o fyzike v pneumatických systémoch
Ako Pascalov zákon určuje výkon sily vo valci?
Pochopenie Pascalovho zákona je základom predpovedania a optimalizácie výkonu valcov v každom pneumatickom systéme.
Pascalov zákon hovorí, že tlak pôsobiaci na kvapalinu v uzavretom systéme sa prenáša rovnomerne do celej kvapaliny. Pre pneumatické valce to znamená, že výstupná sila sa rovná tlaku vynásobenému efektívnou plochou piestu (F = P × A). Tento jednoduchý vzťah je základom všetkých výpočtov sily vo valcoch.

Odvodenie výpočtu sily
Rozoberme si matematické odvodenie výpočtov sily valca:
Základná rovnica sily
Základná rovnica pre silu valca je:
F = P × A
Kde:
- F = výstupná sila (N)
- P = tlak (Pa)
- A = efektívna plocha piestu (m²)
Úvahy o efektívnej oblasti
Účinná plocha sa líši v závislosti od typu a smeru valca:
| Typ valca | Rozširujúca sila | Sila vtiahnutia |
|---|---|---|
| Jednočinný | P × A | Len sila pružiny |
| Dvojčinný (štandardný) | P × A | P × (A - a) |
| Dvojčinný (bez tyče) | P × A | P × A |
Kde:
- A = plná plocha piestu
- a = plocha prierezu tyče
Raz som konzultoval s výrobným závodom v Ohiu, ktorý sa stretával s nedostatočnou silou pri lisovaní. Ich výpočty sa zdali byť na papieri správne, ale skutočný výkon bol nedostatočný. Po prešetrení som zistil, že používajú manometer tlaku2 vo svojich výpočtoch namiesto absolútneho tlaku a nezohľadnili plochu tyče počas vťahovania. Po prepočítaní pomocou správneho vzorca a hodnôt tlaku sme dokázali správne dimenzovať ich systém, čím sa zvýšila produktivita o 23%.
Praktické príklady výpočtu sily
Pozrime sa na niektoré reálne výpočty:
Príklad 1: Rozťahovacia sila v štandardnom valci
Pre valec s:
- Priemer otvoru = 50 mm (polomer = 25 mm = 0,025 m)
- Prevádzkový tlak = 6 barov (600 000 Pa)
Oblasť piestu je:
A = π × r² = π × (0,025)² = 0,001963 m²
Rozširujúca sila je:
F = P × A = 600 000 Pa × 0,001963 m² = 1 178 N ≈ 118 kg sily
Príklad 2: Sila pri vťahovaní v tom istom valci
Ak je priemer tyče 20 mm (polomer = 10 mm = 0,01 m):
Oblasť tyče je:
a = π × r² = π × (0,01)² = 0,000314 m²
Účinná oblasť vťahovania je:
A - a = 0,001963 - 0,000314 = 0,001649 m²
Sila vťahovania je:
F = P × (A - a) = 600 000 Pa × 0,001649 m² = 989 N ≈ 99 kg sily
Faktory účinnosti v reálnych aplikáciách
V praktických aplikáciách ovplyvňuje teoretický výpočet sily niekoľko faktorov:
Straty trením
Trenie medzi tesnením piestu a stenou valca znižuje účinnú silu:
| Typ tesnenia | Typický faktor účinnosti |
|---|---|
| Štandardné NBR | 0.85-0.90 |
| PTFE s nízkym trením | 0.90-0.95 |
| Starnuté/opotrebované tesnenia | 0.70-0.85 |
Praktická rovnica sily
Presnejšia rovnica sily v reálnom svete je:
F_actual = η × P × A
Kde:
- η (eta) = faktor účinnosti (zvyčajne 0,85-0,95)
Aký je vzťah medzi prietokom vzduchu a tlakom vo valcoch?
Pochopenie vzťahu medzi prietokom a tlakom je rozhodujúce pre dimenzovanie systémov na prívod vzduchu a predpovedanie rýchlosti valcov.
Prietok a tlak vzduchu v pneumatických systémoch sú v nepriamom vzťahu - so zvyšujúcim sa tlakom sa zvyčajne znižuje prietok. Tento vzťah sa riadi plynnými zákonmi a je ovplyvnený obmedzeniami, teplotou a objemom systému. Správna prevádzka valca si vyžaduje vyváženie týchto faktorov, aby sa dosiahla požadovaná rýchlosť a sila.
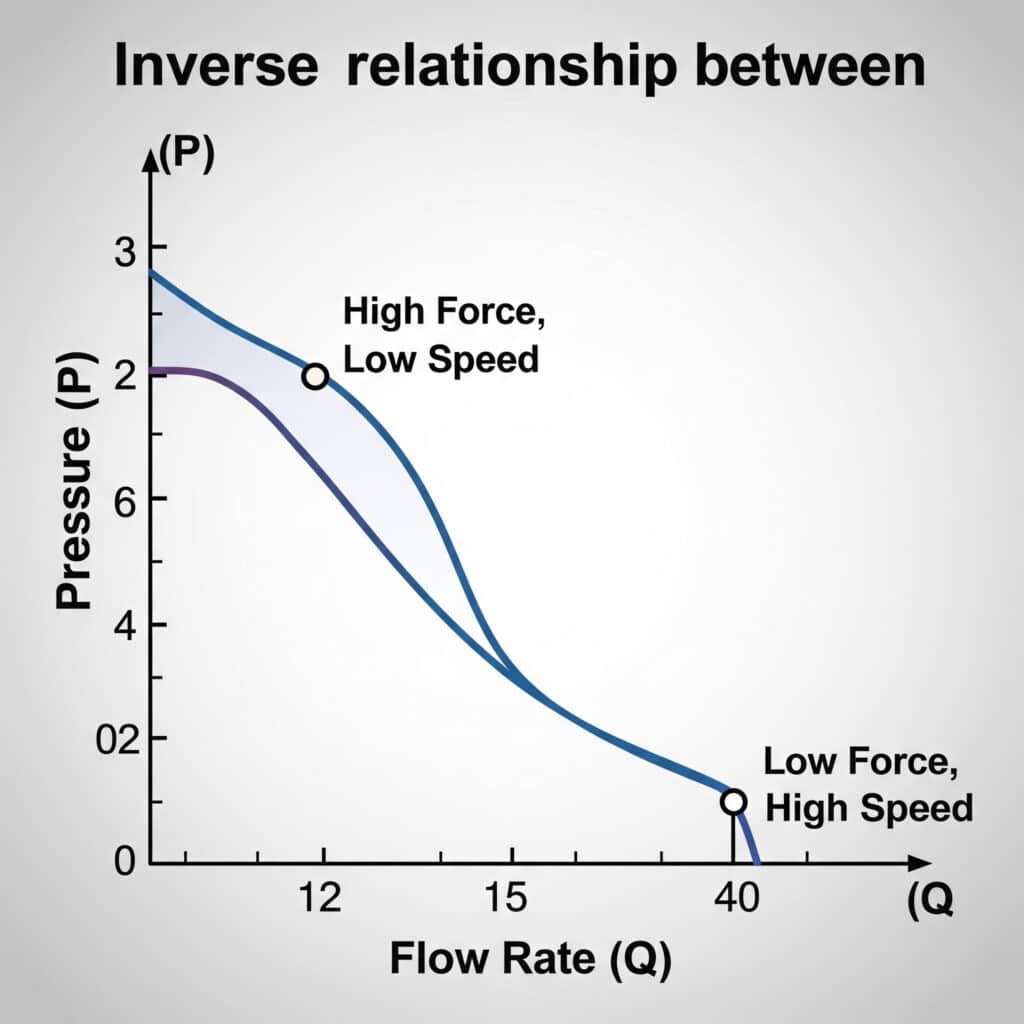
Prevodná tabuľka prietoku a tlaku
V tejto praktickej referenčnej tabuľke je uvedený vzťah medzi prietokom a tlakovou stratou v rôznych komponentoch systému:
| Veľkosť potrubia (mm) | Prietoková rýchlosť (l/min) | Pokles tlaku (bar/meter) pri 6 baroch |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
Matematika prúdenia a tlaku
Vzťah medzi prietokom a tlakom sa riadi niekoľkými plynovými zákonmi:
Poiseuillova rovnica3 pre laminárne prúdenie
Pre laminárne prúdenie v potrubí:
Q = (π × r⁴ × ΔP) / (8 × η × L)
Kde:
- Q = objemový prietok
- r = polomer potrubia
- ΔP = rozdiel tlakov
- η = dynamická viskozita
- L = dĺžka potrubia
Prietokový koeficient (Cv)4 Metóda
Pre komponenty, ako sú ventily:
Q = Cv × √ΔP
Kde:
- Q = prietoková rýchlosť
- Cv = koeficient prietoku
- ΔP = úbytok tlaku na súčiastke
Výpočet otáčok valca
Rýchlosť pneumatického valca závisí od prietoku a plochy valca:
v = Q / A
Kde:
- v = rýchlosť valca (m/s)
- Q = prietok (m³/s)
- A = plocha piestu (m²)
Počas nedávneho projektu v baliarni vo Francúzsku som sa stretol so situáciou, keď sa beztlakové valce klienta pohybovali príliš pomaly napriek dostatočnému tlaku. Analýzou ich systému pomocou našich výpočtov prietoku a tlaku sme identifikovali poddimenzované prívodné potrubia, ktoré spôsobovali značný pokles tlaku. Po modernizácii zo 6 mm na 10 mm rúrky sa ich čas cyklu zlepšil o 40%, čím sa výrazne zvýšila výrobná kapacita.
Kritické aspekty toku
Vzťah prietoku a tlaku v pneumatických systémoch ovplyvňuje niekoľko faktorov:
Fenomén zaduseného toku5
Keď tlakový pomer prekročí kritickú hodnotu (približne 0,53 pre vzduch), prietok sa "zadusí" a nemôže sa zvyšovať bez ohľadu na zníženie tlaku v potrubí.
Vplyv teploty
Prietok je ovplyvnený teplotou podľa vzťahu:
Q₂ = Q₁ × √(T₂/T₁)
Kde:
- Q₁, Q₂ = prietoky pri rôznych teplotách
- T₁, T₂ = absolútne teploty
Prečo je pre návrh systému dôležité porozumieť prepočtu jednotiek tlaku?
Orientácia v rôznych tlakových jednotkách používaných na celom svete je nevyhnutná pre správny návrh systému a medzinárodnú kompatibilitu.
Prepočet jednotiek tlaku je veľmi dôležitý, pretože pneumatické komponenty a špecifikácie používajú rôzne jednotky v závislosti od regiónu a odvetvia. Nesprávna interpretácia jednotiek môže viesť k významným chybám vo výpočtoch s potenciálne nebezpečnými následkami. Prevod medzi absolútnym, manometrickým a diferenčným tlakom pridáva ďalšiu vrstvu zložitosti.
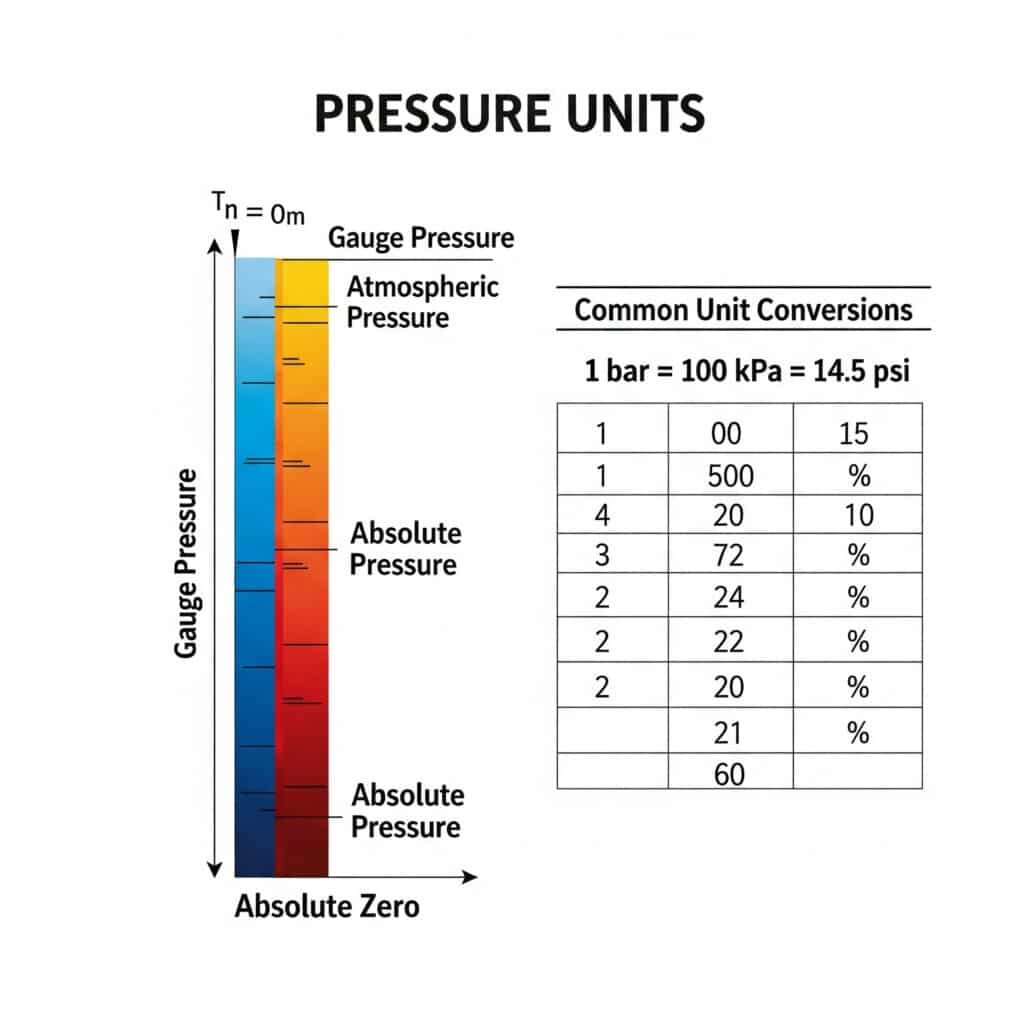
Sprievodca prevodom jednotiek absolútneho tlaku
Táto komplexná prevodná tabuľka pomáha orientovať sa v rôznych jednotkách tlaku používaných na celom svete:
| Jednotka | Symbol | Ekvivalent v Pa | Ekvivalent v baroch | Ekvivalent v psi |
|---|---|---|---|---|
| Pascal | Pa | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| Bar | bar | 1 × 10⁵ | 1 | 14.5038 |
| Libra na štvorcový palec | psi | 6,894.76 | 0.0689476 | 1 |
| Kilogram sily na štvorcový cm | kgf/cm² | 98,066.5 | 0.980665 | 14.2233 |
| Megapascal | MPa | 1 × 10⁶ | 10 | 145.038 |
| Atmosféra | atm | 101,325 | 1.01325 | 14.6959 |
| Torr | Torr | 133.322 | 0.00133322 | 0.0193368 |
| Milimeter ortuti | mmHg | 133.322 | 0.00133322 | 0.0193368 |
| Palec vody | vH₂O | 249.089 | 0.00249089 | 0.0361274 |
Absolútny vs. manometrický tlak
Základom je pochopiť rozdiel medzi absolútnym a manometrickým tlakom:
Kalkulačka prepočtu tlaku
Prevodník jednotiek tlaku
Prevodník prietoku valcov
Konverzné vzorce
- P_absolute = P_gauge + P_atmospheric
- P_gauge = P_absolute - P_atmospheric
Kde je štandardný atmosférický tlak približne:
- 1,01325 bar
- 14,7 psi
- 101 325 Pa
Raz som spolupracoval s tímom inžinierov v Nemecku, ktorí si zakúpili naše bezprúdové valce, ale hlásili, že nedosahujú očakávanú silu. Po vyriešení problémov sme zistili, že používali naše tabuľky sily (ktoré boli založené na manometrickom tlaku), ale zadávali hodnoty absolútneho tlaku. Toto jednoduché nedorozumenie spôsobovalo nesprávny výpočet očakávanej sily o 1 bar. Po objasnení referenčného tlaku ich systém fungoval presne podľa špecifikácie.
Praktické príklady konverzie
Prejdime si niekoľko bežných scenárov konverzie:
Príklad 1: Prepočet pracovného tlaku v jednotkách
Valec dimenzovaný na maximálny pracovný tlak 0,7 MPa:
V bare:
0,7 MPa × 10 bar/MPa = 7 bar
V psi:
0,7 MPa × 145,038 psi/MPa = 101,5 psi
Príklad 2: Prevod z manometra na absolútny tlak
Systém pracujúci pri manometrickom tlaku 6 barov:
V absolútnom tlaku (bar):
6 bar_gauge + 1,01325 bar_atmospheric = 7,01325 bar_absolute
Príklad 3: Prepočet z kgf/cm² na MPa
Japonský valec špecifikovaný na 7 kgf/cm²:
V MPa:
7 kgf/cm² × 0,0980665 MPa/(kgf/cm²) = 0,686 MPa
Preferencie regionálnej tlakovej jednotky
V rôznych regiónoch sa zvyčajne používajú rôzne jednotky tlaku:
| Región | Spoločné tlakové jednotky |
|---|---|
| Severná Amerika | psi, inHg, inH₂O |
| Európa | bar, Pa, mbar |
| Japonsko | kgf/cm², MPa |
| Čína | MPa, bar |
| UK | bar, psi, Pa |
Meranie tlaku v dokumentácii
Pri dokumentovaní špecifikácií tlaku je nevyhnutné jasne uviesť:
- Číselná hodnota
- Merná jednotka
- Či ide o merací (g) alebo absolútny (a) tlak
Napríklad:
- 6 bar_g (manometrický tlak, 6 barov nad atmosférickým)
- 7,01 bar_a (absolútny tlak, celkový tlak vrátane atmosférického)
Záver
Pochopenie fyziky pneumatických valcov - od výpočtov sily podľa Pascalovho zákona až po vzťahy medzi prietokom a tlakom a prevody jednotiek tlaku - je nevyhnutné pre správny návrh systému a riešenie problémov. Tieto základné princípy pomáhajú zabezpečiť, aby vaše pneumatické systémy spoľahlivo a efektívne poskytovali očakávaný výkon.
Často kladené otázky o fyzike v pneumatických systémoch
Ako vypočítam výstupnú silu bezprúdového pneumatického valca?
Ak chcete vypočítať výstupnú silu bezprúdového pneumatického valca, vynásobte prevádzkový tlak efektívnou plochou piestu (F = P × A). Napríklad bezprúdový valec s otvorom 50 mm (plocha 0,001963 m²) pracujúci pri tlaku 6 barov (600 000 Pa) vyvinie silu približne 1 178 N. Na rozdiel od tradičných valcov majú bezprúdové valce zvyčajne rovnakú účinnú plochu v oboch smeroch.
Ako vypočítam výstupnú silu bezprúdového pneumatického valca?
Ak chcete vypočítať výstupnú silu bezprúdového pneumatického valca, vynásobte prevádzkový tlak efektívnou plochou piestu (F = P × A). Napríklad bezprúdový valec s otvorom 50 mm (plocha 0,001963 m²) pracujúci pri tlaku 6 barov (600 000 Pa) vyvinie silu približne 1 178 N. Na rozdiel od tradičných valcov majú bezprúdové valce zvyčajne rovnakú účinnú plochu v oboch smeroch.
Aký je rozdiel medzi manometrickým a absolútnym tlakom?
Manometrický tlak (bar_g, psi_g) meria tlak vzhľadom na atmosférický tlak, pričom atmosférický tlak je nula. Absolútny tlak (bar_a, psi_a) meria tlak vzhľadom na dokonalé vákuum, ktoré je nulové. Ak chcete prepočítať manometrický tlak na absolútny tlak, pripočítajte k údaju manometra atmosférický tlak (približne 1,01325 baru alebo 14,7 psi).
Ako ovplyvňuje prietok vzduchu rýchlosť valcov?
Otáčky valca sú priamo úmerné prietoku vzduchu a nepriamo úmerné ploche piestu (v = Q/A). Nedostatočný prietok spôsobený poddimenzovaným prívodným potrubím, obmedzujúcimi armatúrami alebo nevhodnými ventilmi obmedzí rýchlosť valca bez ohľadu na tlak. Napríklad pri prietoku 20 litrov za sekundu cez valec s plochou piestu 0,002 m² sa dosiahne rýchlosť 10 metrov za sekundu.
Prečo sa pneumatické valce niekedy pohybujú pomalšie, ako sa vypočítalo?
Pneumatické valce sa môžu pohybovať pomalšie, ako bolo vypočítané, a to v dôsledku niekoľkých faktorov: obmedzenia prívodu vzduchu spôsobujúce pokles tlaku, vnútorné trenie tesnení, mechanické zaťaženie presahujúce výpočty, netesnosť znižujúca účinný tlak alebo vplyv teploty na hustotu vzduchu. Okrem toho prietokové koeficienty ventilov často obmedzujú skutočný prietok dostupný pre valec.
Ako môžem previesť rôzne jednotky tlaku pre medzinárodné špecifikácie?
Na prevod medzi jednotkami tlaku použite násobiace faktory: 1 bar = 100 000 Pa = 0,1 MPa = 14,5038 psi = 1,01972 kgf/cm². Vždy si overte, či je tlak uvedený ako manometrický alebo absolútny, pretože tento rozdiel môže výrazne ovplyvniť výpočty. Napríklad 6 bar_g sa rovná 7,01325 bar_a pri štandardných atmosférických podmienkach.
Aký je vzťah medzi veľkosťou otvoru valca a silovým výkonom?
Vzťah medzi veľkosťou otvoru valca a silovým výkonom je kvadratický - zdvojnásobením priemeru otvoru sa silový výkon zvýši štvornásobne (keďže plocha = π × r²). Napríklad pri prevádzkovom tlaku 6 barov valec s priemerom otvoru 40 mm vyvinie silu približne 754 N, zatiaľ čo valec s priemerom otvoru 80 mm vyvinie silu približne 3 016 N, čo je takmer štyrikrát viac.
-
Poskytuje podrobné vysvetlenie Pascalovho zákona, základného princípu mechaniky kvapalín, ktorý je základom hydraulického a pneumatického prenosu energie. ↩
-
Ponúka jasnú definíciu a porovnanie merného a absolútneho tlaku, čo je rozhodujúce pre presné technické výpočty, pretože merný tlak je relatívny voči atmosférickému tlaku. ↩
-
Vysvetľuje odvodenie a aplikáciu Poiseuillovho zákona, ktorý opisuje pokles tlaku nestlačiteľnej a newtonovskej kvapaliny prúdiacej cez dlhé valcové potrubie v laminárnom režime. ↩
-
Poskytuje technickú definíciu prietokového koeficientu (Cv), imperiálnej miery, ktorá poskytuje štandardizovaný spôsob porovnávania prietokových kapacít rôznych ventilov. ↩
-
Podrobne opisuje fyzikálne vlastnosti dusivého prúdenia, čo je podmienka dynamiky tekutín, ktorá obmedzuje hmotnostný prietok stlačiteľnej tekutiny cez obmedzenie, keď rýchlosť dosiahne rýchlosť zvuku. ↩



