
Už ste sa niekedy dotkli pneumatický valec po nepretržitej prevádzke a prekvapilo vás, aké je horúce? Toto teplo nie je len nepríjemnosť - predstavuje plytvanie energiou, zníženú účinnosť a potenciálne problémy so spoľahlivosťou, ktoré môžu vašu prevádzku stáť tisíce.
Prenos tepla v pneumatických systémoch sa uskutočňuje tromi mechanizmami: vedením cez materiály komponentov, konvekciou medzi povrchmi a vzduchom a vyžarovaním z horúcich povrchov. Pochopenie a optimalizácia týchto princípov môže znížiť prevádzkové teploty o 15-30%, predĺžiť životnosť komponentov až o 40% a zlepšiť energetickú účinnosť o 5-15%.
Minulý mesiac som poskytoval konzultácie pre potravinársky závod v Georgii, kde beztlakové fľaše zlyhávali každé 3 - 4 mesiace kvôli tepelným problémom. Ich tím údržby jednoducho vymieňal komponenty bez toho, aby riešil hlavnú príčinu. Uplatnením správnych zásad prenosu tepla sme znížili prevádzkové teploty o 22 °C a predĺžili životnosť komponentov na viac ako rok. Dovoľte mi, aby som vám ukázal, ako sme to dokázali - a ako môžete rovnaké princípy uplatniť na svoje systémy.
Obsah
- Výpočet koeficientu vodivosti: Ako sa teplo pohybuje cez vaše komponenty?
- Metódy zlepšenia konvekcie: Aké techniky maximalizujú prenos tepla zo vzduchu na povrch?
- Model účinnosti žiarenia: Kedy má tepelné vyžarovanie v pneumatických systémoch význam?
- Záver
- Často kladené otázky o prenose tepla v pneumatických systémoch
Výpočet koeficientu vodivosti: Ako sa teplo pohybuje cez vaše komponenty?
Kondukcia je primárnym mechanizmom prenosu tepla v pevných pneumatických komponentoch. Pochopenie spôsobu výpočtu a optimalizácie koeficientov vedenia je nevyhnutné na riadenie teplôt v systéme.
Súčiniteľ vedenia tepla možno vypočítať pomocou Fourierov zákon1: q = -k(dT/dx), kde q je tepelný tok (W/m²), k je tepelná vodivosť (W/m-K) a dT/dx je teplotný gradient. V prípade pneumatických komponentov závisí efektívna vodivosť od výberu materiálu, kvality rozhrania a geometrických faktorov, ktoré ovplyvňujú dĺžku tepelnej cesty a plochu prierezu.
Pamätám si, ako som riešil problémy na výrobnej linke v Tennessee, kde predčasne zlyhávali ložiská valcov bez tyčí. Tím údržby vyskúšal viacero mazív bez úspechu. Keď sme analyzovali cesty vedenia, objavili sme tepelné úzke miesto na rozhraní ložiska a krytu. Zlepšením povrchovej úpravy a použitím tepelne vodivej zmesi sme zvýšili účinný koeficient vodivosti o 340% a úplne odstránili poruchy.
Základné rovnice vedenia
Rozoberme si kľúčové rovnice na výpočet vedenia v pneumatických komponentoch:
Fourierov zákon pre vedenie tepla
Základná rovnica pre vedenie tepla je:
q = -k(dT/dx)
Kde:
- q = tepelný tok (W/m²)
- k = tepelná vodivosť (W/m-K)
- dT/dx = teplotný gradient (K/m)
Pre jednoduchý jednorozmerný prípad s konštantným prierezom:
Q = kA(T₁-T₂)/L
Kde:
- Q = rýchlosť prenosu tepla (W)
- A = plocha prierezu (m²)
- T₁, T₂ = teploty na každom konci (K)
- L = dĺžka tepelnej cesty (m)
Koncepcia tepelného odporu
Pri zložitých geometriách je často praktickejší prístup založený na tepelnom odpore:
R = L/(kA)
Kde:
- R = tepelný odpor (K/W)
Pre systémy s viacerými komponentmi v sérii:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
A rýchlosť prestupu tepla sa stáva:
Q = ΔT/Rcelkom
Porovnanie tepelnej vodivosti materiálu
| Materiál | Tepelná vodivosť (W/m-K) | Relatívna vodivosť | Bežné aplikácie |
|---|---|---|---|
| Hliník | 205-250 | Vysoká | Valce, chladiče |
| Oceľ | 36-54 | Stredné | Štrukturálne komponenty |
| Nerezová oceľ | 14-16 | Nízka a stredná úroveň | Korózne prostredia |
| Bronz | 26-50 | Stredné | Ložiská, puzdrá |
| PTFE | 0.25 | Veľmi nízka | Tesnenia, ložiská |
| Nitrilová guma | 0.13 | Veľmi nízka | O-krúžky, tesnenia |
| Vzduch (nehybný) | 0.026 | Extrémne nízka | Výplň medzier |
| Tepelná pasta | 3-8 | Nízka | Materiál rozhrania |
Kontaktný odpor v pneumatických zostavách
Na rozhraniach medzi komponentmi má kontaktný odpor významný vplyv na prenos tepla:
Rkontakt = 1/(hc × A)
Kde:
- hc = kontaktný koeficient (W/m²-K)
- A = kontaktná plocha (m²)
Medzi faktory ovplyvňujúce kontaktný odpor patria:
- Drsnosť povrchu: Drsnejšie povrchy majú menšiu skutočnú kontaktnú plochu
- Kontakt Tlak: Vyšší tlak zvyšuje efektívnu kontaktnú plochu
- Materiály rozhrania: Tepelné zmesi vypĺňajú vzduchové medzery
- Čistota povrchu: Kontaminanty môžu zvýšiť odolnosť
Prípadová štúdia: Tepelná optimalizácia valcov bez tyčí
Pre magnetický valec bez tyče, ktorý má tepelné problémy:
| Komponent | Pôvodný dizajn | Optimalizovaný dizajn | Zlepšenie |
|---|---|---|---|
| Teleso valca | eloxovaný hliník | Rovnaký materiál, vylepšená povrchová úprava | 15% lepšia vodivosť |
| Rozhranie ložiska | Kontakt kov na kov | Pridaná tepelná zmes | 340% lepšia vodivosť |
| Montážne konzoly | Lakovaná oceľ | Holý hliník | 280% lepšia vodivosť |
| Celkový tepelný odpor | 2,8 K/W | 0,7 K/W | Redukcia 75% |
| Prevádzková teplota | 78°C | 56°C | Zníženie o 22 °C |
| Životnosť súčasti | 4 mesiace | >12 mesiacov | 3× zlepšenie |
Praktické techniky optimalizácie vedenia
Na základe mojich skúseností so stovkami pneumatických systémov uvádzam najúčinnejšie prístupy na zlepšenie vodivosti:
Optimalizácia rozhrania
- Povrchová úprava: Zlepšenie hladkosti povrchu na Ra 0,4-0,8 μm
- Materiály tepelného rozhrania2: Použite vhodné zmesi (3-8 W/m-K)
- Upevňovací moment: Zabezpečte správne utiahnutie pre optimálny prítlak
- Čistota: Pred montážou odstráňte všetky oleje a nečistoty
Stratégie výberu materiálu
- Kritické tepelné dráhy: Používajte vysoko vodivé materiály (hliník, meď)
- Tepelné prestávky: Zámerne používajte materiály s nízkou vodivosťou na izoláciu tepla
- Zložené prístupy: Kombinácia materiálov pre optimálny výkon/náklady
- Anizotropné materiály: V prípade potreby využite smerovú vodivosť
Geometrická optimalizácia
- Dĺžka tepelnej cesty: Minimalizujte vzdialenosť medzi zdrojmi tepla a chladičmi
- Prierezová plocha: Maximalizujte plochu kolmo na tepelný tok
- Tepelné prekážky: Identifikujte a odstráňte zúženia na tepelnej dráhe
- Zbytočné cesty: Vytvorenie viacerých paralelných vodiacich trás
Metódy zlepšenia konvekcie: Aké techniky maximalizujú prenos tepla zo vzduchu na povrch?
Konvekcia je často limitujúcim faktorom pri chladení pneumatických systémov. Zlepšenie konvekčného prenosu tepla môže výrazne zlepšiť tepelný manažment a výkon systému.
Nasleduje konvekčný prenos tepla Newtonov zákon chladenia3: Q = hA(Ts-T∞), kde h je koeficient konvekcie (W/m²-K), A je plocha povrchu a (Ts-T∞) je rozdiel teplôt medzi povrchom a tekutinou. Metódy vylepšenia zahŕňajú zväčšenie plochy povrchu pomocou rebier, zlepšenie rýchlosti kvapaliny pomocou usmerneného prúdenia vzduchu a optimalizáciu vlastností povrchu na podporu turbulentných hraničných vrstiev.
Počas auditu energetickej účinnosti v baliacej prevádzke v Arizone som sa stretol s pneumatickým systémom, ktorý pracoval v prostredí s teplotou 43 °C. Ich bezprúdové valce sa prehrievali napriek tomu, že spĺňali všetky požiadavky na údržbu. Zavedením cieleného zlepšenia konvekcie - pridaním malých hliníkových rebier a ventilátora s nízkou spotrebou energie - sme zvýšili koeficient konvekcie o 450%. Tým sa znížili prevádzkové teploty z nebezpečných úrovní na hodnoty v rámci špecifikácie bez akýchkoľvek väčších úprav systému.
Základy konvekčného prenosu tepla
Základná rovnica, ktorou sa riadi konvekčný prenos tepla, je:
Q = hA(Ts-T∞)
Kde:
- Q = rýchlosť prenosu tepla (W)
- h = koeficient konvekcie (W/m²-K)
- A = plocha povrchu (m²)
- Ts = povrchová teplota (K)
- T∞ = teplota kvapaliny (vzduchu) (K)
Koeficient konvekcie h závisí od viacerých faktorov:
- Vlastnosti kvapaliny (hustota, viskozita, tepelná vodivosť)
- Charakteristiky prúdenia (rýchlosť, turbulencia)
- Geometria a orientácia povrchu
- Režim prúdenia (prirodzená a vynútená konvekcia)
Prirodzená vs. nútená konvekcia
| Parameter | Prirodzená konvekcia | Nútená konvekcia | Dôsledky |
|---|---|---|---|
| Typická hodnota h | 5-25 W/m²-K | 25-250 W/m²-K | Nútená konvekcia môže byť 10× účinnejšia |
| Hnacia sila | Vztlak (teplotný rozdiel) | Vonkajší tlak (ventilátory, dúchadlá) | Nútená konvekcia je menej závislá od teploty |
| Vzor toku | Vertikálne prúdenie pozdĺž povrchov | Smerové na základe mechanizmu forsírovania | Nútený prietok možno optimalizovať pre konkrétne komponenty |
| Spoľahlivosť | Pasívny, vždy prítomný | Vyžaduje napájanie a údržbu | Prirodzená konvekcia poskytuje základné chladenie |
| Požiadavky na priestor | Vyžaduje voľný priestor pre cirkuláciu vzduchu | Vyžaduje priestor pre vzduchotechnické zariadenia a potrubia | Nútené systémy potrebujú viac plánovania |
Techniky na zlepšenie konvekcie
Zväčšenie plochy
Zvyšovanie účinnej plochy prostredníctvom:
Plutvy a rozšírené plochy
- Kolíkové plutvy: Všesmerové prúdenie vzduchu, zväčšenie plochy 150-300%
- Doskové plutvy: Smerové prúdenie vzduchu, zväčšenie plochy 200-500%
- Vlnité povrchy: 50-150% zväčšenie plochyZdrsnenie povrchu
- Mikrotextúra: 5-15% zvýšenie efektívnej plochy
- Dimpled surfaces: 10-30% increase plus boundary layer effects
- Drážkované vzory: 15-40% zvýšenie so smerovými výhodami
Manipulácia s tokom
Zlepšenie vlastností prúdenia vzduchu prostredníctvom:
Systémy s núteným prívodom vzduchu
- Ventilátory: Smerové prúdenie vzduchu, 200-600% h zlepšenie
- Dúchadlá: Vysokotlakový prietok, 300-800% h zlepšenie
- Stlačené vzduchové trysky: 400-1000% miestne zlepšenie hOptimalizácia trasy toku
- Baffles: Nasmerujte vzduch ku kritickým komponentom
- Venturiho efekt: Zrýchlenie vzduchu cez špecifické povrchy
- Vírové generátory: Vytvárajte turbulencie na narušenie hraničnej vrstvy
Úpravy povrchu
Zmena vlastností povrchu na zlepšenie konvekcie:
Ošetrenie emisivity
- Čierny oxid: Zvyšuje emisivitu na 0,7-0,9
- Eloxovanie: Kontrolovaná emisivita od 0,4-0,9
- Farby a nátery: Prispôsobiteľná emisivita až do 0,98Kontrola zmáčavosti
- Hydrofilné nátery: Zlepšujú chladenie kvapalinami
- Hydrofóbne povrchy: Zabráňte problémom s kondenzáciou
- Vzorovaná zmáčavosť: Usmernený tok kondenzátu
Praktický príklad implementácie
Pre bezprúdový pneumatický valec pracujúci v prostredí s vysokou teplotou:
| Metóda vylepšenia | Implementácia | h Zlepšenie | Zníženie teploty |
|---|---|---|---|
| Kolíkové plutvy (6 mm) | Hliníkové plutvy s rozstupom 10 mm | 180% | 12°C |
| Usmernené prúdenie vzduchu | 80 mm, 2 W ventilátor DC s rýchlosťou 1,5 m/s | 320% | 18°C |
| Povrchová úprava | Čierne eloxovanie | 40% | 3°C |
| Kombinovaný prístup | Všetky metódy integrované | 450% | 24°C |
Korelácia Nusseltovho čísla pre konštrukčné výpočty
Pri technických výpočtoch sa Nusseltovo číslo4 (Nu) poskytuje bezrozmerný prístup ku konvekcii:
Nu = hL/k
Kde:
- L = charakteristická dĺžka
- k = tepelná vodivosť kvapaliny
Pre nútenú konvekciu nad plochou doskou:
Nu = 0,664Re^(1/2)Pr^(1/3) (laminárne prúdenie)
Nu = 0,037Re^(4/5)Pr^(1/3) (turbulentné prúdenie)
Kde:
- Re = Reynoldsovo číslo (rýchlosť × dĺžka × hustota / viskozita)
- Pr = Prandtlovo číslo (merné teplo × viskozita / tepelná vodivosť)
Tieto korelácie umožňujú inžinierom predpovedať konvekčné koeficienty pre rôzne konfigurácie a podľa toho optimalizovať stratégie chladenia.
Model účinnosti žiarenia: Kedy má tepelné vyžarovanie v pneumatických systémoch význam?
Sálanie sa pri tepelnom manažmente pneumatických systémov často prehliada, ale v mnohých aplikáciách môže predstavovať 15-30% celkového prenosu tepla. Pochopenie toho, kedy a ako optimalizovať sálavý prenos tepla, je pre komplexný tepelný manažment kľúčové.
Prenos tepla sálaním sa riadi Stefan-Boltzmannov zákon5: Q = εσA(T₁⁴-T₂⁴), kde ε je emisivita povrchu, σ je Stefanova-Boltzmannova konštanta, A je plocha povrchu a T₁ a T₂ sú absolútne teploty vyžarujúceho povrchu a okolia. Účinnosť vyžarovania v pneumatických systémoch závisí predovšetkým od emisivity povrchu, rozdielu teplôt a činiteľov pohľadu medzi komponentmi a ich okolím.
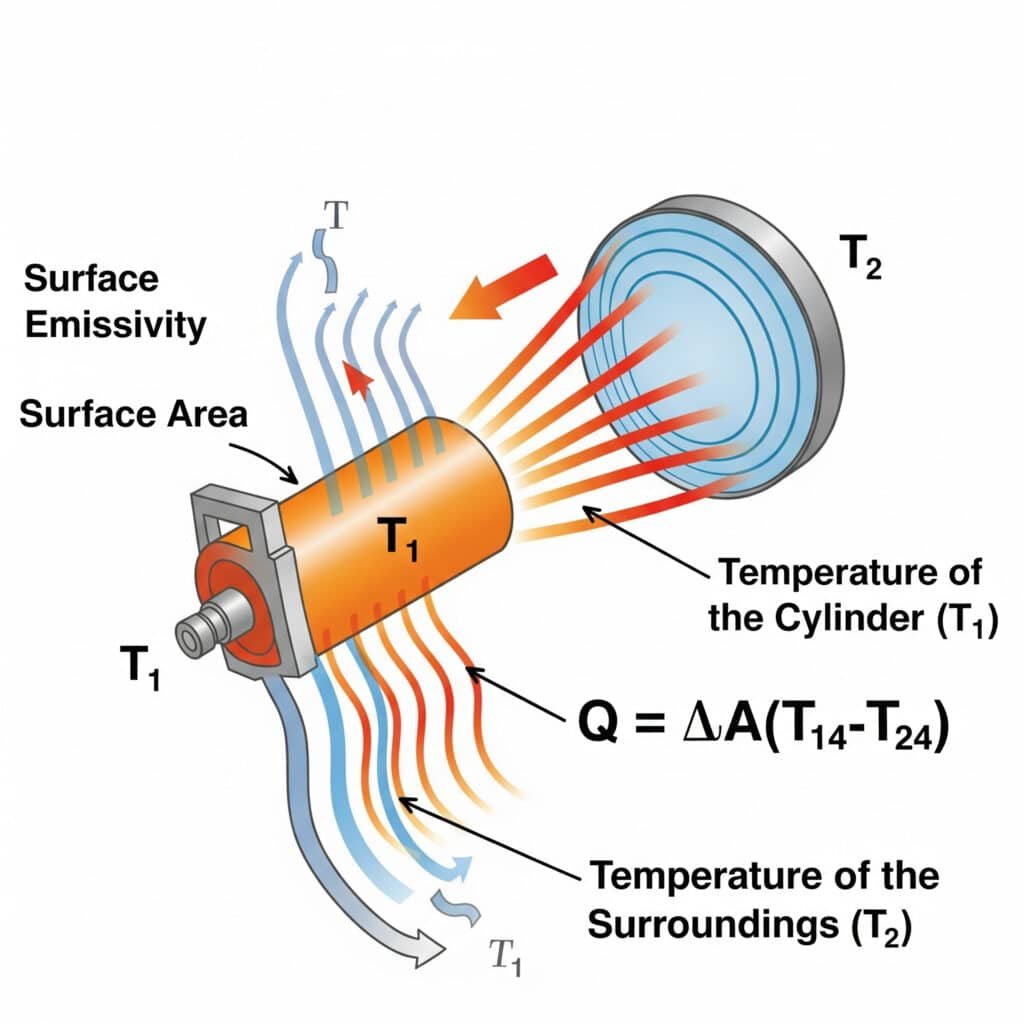
Nedávno som pomohol výrobcovi polovodičových zariadení v Oregone vyriešiť problémy s prehrievaním ich presných bezšnúrových valcov. Ich inžinieri sa zameriavali výlučne na vedenie a konvekciu, ale prehliadali žiarenie. Nanesením vysokoemisívneho povlaku (zvýšenie ε z 0,11 na 0,92) sme zlepšili sálavý prenos tepla o viac ako 700%. Toto jednoduché, pasívne riešenie znížilo prevádzkovú teplotu o 9 °C bez akýchkoľvek pohyblivých častí alebo spotreby energie - čo je kritická požiadavka v ich prostredí čistých priestorov.
Základy prenosu tepla sálaním
Základná rovnica, ktorou sa riadi sálavý prenos tepla, je:
Q = εσA(T₁⁴-T₂⁴)
Kde:
- Q = rýchlosť prenosu tepla (W)
- ε = emisivita (bezrozmerná, 0-1)
- σ = Stefanova-Boltzmannova konštanta (5,67 × 10-⁸ W/m²-K⁴)
- A = plocha povrchu (m²)
- T₁ = absolútna teplota povrchu (K)
- T₂ = absolútna teplota okolia (K)
Hodnoty emisivity povrchu pre bežné pneumatické materiály
| Materiál/povrch | Emisivita (ε) | Účinnosť žiarenia | Potenciál vylepšenia |
|---|---|---|---|
| Leštený hliník | 0.04-0.06 | Veľmi zlé | >1500% možné zlepšenie |
| eloxovaný hliník | 0.7-0.9 | Vynikajúce | Už optimalizované |
| Nerezová oceľ (leštená) | 0.07-0.14 | Chudobný | >600% možné zlepšenie |
| Nerezová oceľ (oxidovaná) | 0.6-0.85 | Dobrý | Možné mierne zlepšenie |
| Oceľ (leštená) | 0.07-0.10 | Chudobný | >900% možné zlepšenie |
| Oceľ (oxidovaná) | 0.7-0.9 | Vynikajúce | Už optimalizované |
| Maľované povrchy | 0.8-0.98 | Vynikajúce | Už optimalizované |
| PTFE (biely) | 0.8-0.9 | Vynikajúce | Už optimalizované |
| Nitrilová guma | 0.86-0.94 | Vynikajúce | Už optimalizované |
Zobrazenie faktorov
Výmena žiarenia závisí nielen od emisivity, ale aj od geometrických vzťahov medzi povrchmi:
F₁₂ = podiel žiarenia, ktoré opúšťa povrch 1 a dopadá na povrch 2
V prípade zložitých geometrií možno faktory pohľadu vypočítať pomocou:
- Analytické riešenia pre jednoduché geometrie
- Zobraziť faktorovú algebru na kombináciu známych riešení
- Numerické metódy pre komplexné usporiadanie
- Empirické aproximácie pre praktické inžinierstvo
Závislosť žiarenia od teploty
Teplotný vzťah štvrtej mocniny spôsobuje, že žiarenie je účinné najmä pri vyšších teplotách:
| Povrchová teplota | Percento prenosu tepla sálaním* |
|---|---|
| 30 °C (303 K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100 °C (373 K) | 25-45% |
| 150 °C (423 K) | 35-60% |
*Predpokladajúc podmienky prirodzenej konvekcie, ε = 0,8, 25 °C okolia
Stratégie na zvýšenie účinnosti žiarenia
Na základe mojich skúseností s priemyselnými pneumatickými systémami uvádzam najúčinnejšie prístupy na zlepšenie prenosu tepla žiarením:
Modifikácia emisivity povrchu
Povlaky s vysokou emisivitou
- Čierne eloxovanie hliníka (ε ≈ 0,8-0,9)
- Čierny oxid pre oceľ (ε ≈ 0,7-0,8)
- Špeciálne keramické povlaky (ε ≈ 0,9-0,98)Textúrovanie povrchu
- Mikrodrsnenie zvyšuje efektívnu emisivitu
- Porézne povrchy zlepšujú radiačné vlastnosti
- Kombinované vylepšenia emisivity/konvekcie
Optimalizácia životného prostredia
Riadenie teploty okolia
- Tienenie pred horúcimi zariadeniami/procesmi
- Chladné steny/stropy pre lepšiu výmenu žiarenia
- Reflexné bariéry na presmerovanie žiarenia na chladnejšie povrchyZobrazenie faktora Zlepšenie
- Orientácia na maximalizáciu vystavenia chladným povrchom
- Odstránenie blokujúcich predmetov
- Reflektory na zlepšenie výmeny žiarenia s chladnejšími oblasťami
Prípadová štúdia: Zlepšenie žiarenia v presnej pneumatike
Pre vysoko presný bezprúdový valec v prostredí čistých priestorov:
| Parameter | Pôvodný dizajn | Dizajn so zvýšeným vyžarovaním | Zlepšenie |
|---|---|---|---|
| Povrchový materiál | Leštený hliník (ε ≈ 0,06) | Hliník s keramickým povlakom (ε ≈ 0,94) | 1467% zvýšenie emisivity |
| Prenos tepla sálaním | 2.1W | 32.7W | 1457% zvýšenie žiarenia |
| Prevádzková teplota | 68°C | 59°C | Zníženie o 9 °C |
| Životnosť súčasti | 8 mesiacov | >24 mesiacov | 3× zlepšenie |
| Náklady na implementáciu | – | $175 na valec | Návratnosť 4,2 mesiaca |
Sálanie vs. iné spôsoby prenosu tepla
Pre účinný tepelný manažment je veľmi dôležité pochopiť, kedy dominuje žiarenie:
| Stav | Dominancia vedenia | Dominancia konvekcie | Dominancia žiarenia |
|---|---|---|---|
| Teplotný rozsah | Nízka až vysoká | Nízka až stredná | Stredná až vysoká |
| Vlastnosti materiálu | Materiály s vysokým k | Nízke k, vysoký povrch | Vysoké ε povrchy |
| Faktory životného prostredia | Dobrý tepelný kontakt | Pohybujúci sa vzduch, ventilátory | Veľký teplotný rozdiel |
| Priestorové obmedzenia | Pevné balenie | Otvorené prúdenie vzduchu | Výhľad na chladnejšie okolie |
| Najlepšie aplikácie | Rozhrania komponentov | Všeobecné chladenie | Horúce povrchy, vákuum, nehybný vzduch |
Záver
Zvládnutie princípov prenosu tepla - výpočet súčiniteľa vedenia, metódy zlepšenia konvekcie a modelovanie účinnosti žiarenia - poskytuje základ pre efektívne riadenie tepla v pneumatických systémoch. Uplatňovaním týchto princípov môžete znížiť prevádzkové teploty, predĺžiť životnosť komponentov a zlepšiť energetickú účinnosť a zároveň zabezpečiť spoľahlivú prevádzku aj v náročných podmienkach.
Často kladené otázky o prenose tepla v pneumatických systémoch
Aký je typický nárast teploty v pneumatických valcoch počas prevádzky?
Pneumatické valce počas nepretržitej prevádzky zvyčajne vykazujú nárast teploty o 20-40 °C nad okolitú teplotu. Toto zvýšenie je dôsledkom trenia medzi tesneniami a stenami valca, kompresného ohrevu vzduchu a mechanickej práce, ktorá sa premieňa na teplo. V bezprúdových valcoch často dochádza k vyššiemu nárastu teploty (30 - 50 °C) v dôsledku ich zložitejších tesniacich systémov a koncentrovanej tvorby tepla v sústave ložisko/tesnenie.
Ako ovplyvňuje prevádzkový tlak vznik tepla v pneumatických systémoch?
Prevádzkový tlak má významný vplyv na tvorbu tepla, pričom vyšší tlak vytvára viac tepla prostredníctvom niekoľkých mechanizmov. Každé zvýšenie prevádzkového tlaku o 1 bar zvyčajne zvyšuje tvorbu tepla o 8-12% v dôsledku väčších trecích síl medzi tesneniami a povrchmi, vyššieho kompresného ohrevu a zvýšených strát súvisiacich s netesnosťami. Tento vzťah je približne lineárny v rámci bežných prevádzkových rozsahov (3 - 10 barov).
Aký je optimálny spôsob chladenia pneumatických komponentov v rôznych prostrediach?
Optimálny prístup k chladeniu sa líši podľa prostredia: v čistom prostredí s miernou teplotou (15 - 30 °C) často postačuje prirodzená konvekcia so správnym rozmiestnením komponentov. V prostredí s vysokou teplotou (30-50 °C) je potrebná nútená konvekcia pomocou ventilátorov alebo stlačeného vzduchu. V extrémne horúcich podmienkach (>50 °C) alebo tam, kde je obmedzené prúdenie vzduchu, môžu byť potrebné aktívne metódy chladenia, ako sú termoelektrické chladiče alebo kvapalinové chladenie. Vo všetkých prípadoch poskytuje dodatočné pasívne chladenie maximalizácia vyžarovania prostredníctvom povrchov s vysokou emisivitou.
Ako vypočítam celkový prenos tepla z pneumatického komponentu?
Vypočítajte celkový prenos tepla sčítaním príspevkov z každého mechanizmu: Qtotal = Qconduction + Qconvection + Qradiation. Pre vedenie použite Q = kA(T₁-T₂)/L pre každú cestu tepla. Pre konvekciu použite Q = hA(Ts-T∞) s príslušnými koeficientmi konvekcie. Pre žiarenie použite Q = εσA(T₁⁴-T₂⁴). Vo väčšine priemyselných pneumatických aplikácií pracujúcich pri 30-80 °C je približné rozdelenie 20-40% vedenia, 40-70% konvekcie a 10-30% žiarenia.
Aký je vzťah medzi teplotou a životnosťou pneumatických komponentov?
Životnosť súčiastky exponenciálne klesá s rastúcou teplotou podľa modifikovaného Arrheniovho vzťahu. Platí pravidlo, že každé zvýšenie prevádzkovej teploty o 10 °C znižuje životnosť tesnenia a komponentov o 40-50%. To znamená, že komponent pracujúci pri teplote 70 °C môže mať len tretinovú životnosť v porovnaní s tým istým komponentom pri teplote 50 °C. Tento vzťah je obzvlášť kritický pre polymérové komponenty, ako sú tesnenia, ložiská a tesnenia, ktoré často určujú interval údržby pneumatických systémov.
-
Poskytuje základné vysvetlenie Fourierovho zákona, základného princípu, ktorý opisuje spôsob vedenia tepla cez pevné materiály na základe ich tepelnej vodivosti a teplotného gradientu. ↩
-
Vysvetľuje funkciu a typy materiálov tepelného rozhrania (TIM), ktoré sa používajú na vyplnenie mikroskopických vzduchových medzier medzi komponentmi s cieľom zlepšiť vedenie tepla a znížiť tepelný odpor. ↩
-
Podrobnosti o princípoch Newtonovho zákona chladenia, ktorý upravuje spôsob chladenia objektov odovzdávaním tepla okolitej kvapaline prostredníctvom konvekcie, čo je kľúčový faktor pri návrhu chladiaceho systému. ↩
-
Ponúka podrobný pohľad na Nusseltovo číslo, kritickú bezrozmernú veličinu v dynamike tekutín a prenose tepla, ktorá predstavuje pomer konvekčného a vodivého prenosu tepla cez hranicu. ↩
-
Opisuje Stefan-Boltzmannov zákon, základný fyzikálny princíp, ktorý kvantifikuje celkovú energiu vyžiarenú čiernym telesom, čo je nevyhnutné na výpočet tepelných strát z horúcich povrchov. ↩



