Har du problem med luftläckage i dina pneumatiska system? Du är inte ensam om det. Många ingenjörer kämpar med tätningsfel som orsakar effektivitetsförluster, ökade underhållskostnader och oväntade driftstopp. Rätt kunskap om tätningsmekanismer kan lösa dessa ihållande problem.
Tätningsmekanismer i pneumatiska system fungerar genom kontrollerad deformation av elastomeriska material1 mot motstående ytor. Effektiva tätningar upprätthåller kontakttrycket genom kompression (statiska tätningar) eller genom en balans mellan tryck, friktion och smörjning (dynamiska tätningar), vilket skapar en ogenomtränglig barriär mot luftläckage.
Jag har arbetat med pneumatiska system i över 15 år på Bepto, och jag har sett otaliga fall där förståelse för tätningsprinciper har sparat företag tusentals kronor i underhållskostnader och förhindrat katastrofala systemfel.
Innehållsförteckning
- Hur påverkar O-ringens kompressionsförhållande tätningens prestanda?
- Varför är Stribeck-kurvan viktig för design av pneumatiska tätningar?
- Vad orsakar friktionsuppvärmning i dynamiska tätningar och hur kan den kontrolleras?
- Slutsats
- Vanliga frågor om pneumatiska tätningsmekanismer
Hur påverkar O-ringens kompressionsförhållande tätningens prestanda?
O-ringar är kanske de vanligaste tätningselementen i pneumatiska system, men bakom deras enkla utseende döljer sig komplexa tekniska principer. Kompressionsförhållandet är avgörande för deras prestanda och livslängd.
O-ringens kompressionsförhållande är den procentuella deformationen från det ursprungliga tvärsnittet när den är installerad. För optimal prestanda krävs normalt en kompression på 15-30%. För liten kompression orsakar läckage, medan överdriven kompression leder till förtida fel genom extrudering, kompressionsuppsättning2eller påskyndat slitage.

Att få rätt kompressionsförhållande är mer nyanserat än vad många ingenjörer inser. Låt mig dela med mig av några praktiska insikter från min erfarenhet av stånglösa cylindertätningssystem.
Beräkning av det optimala kompressionsförhållandet för O-ringar
Beräkningen av kompressionsförhållandet verkar enkel:
| Parameter | Formel | Exempel |
|---|---|---|
| Kompressionsförhållande (%) | [(d - g)/d] × 100 | För 2,5 mm O-ring i 2,0 mm spår: [(2,5 - 2,0)/2,5] × 100 = 20% |
| Pressning (mm) | d - g | 2,5 mm - 2,0 mm = 0,5 mm |
| Fyllning av spår (%) | [π(d/2)²]/[w × g] × 100 | För 2,5 mm O-ring i 3,5 mm brett och 2,0 mm djupt spår: [π(2,5/2)²]/[3,5 × 2,0] × 100 = 70% |
Var?
- d = O-ringens tvärsnittsdiameter
- g = spårdjup
- w = spårets bredd
Materialspecifika riktlinjer för komprimering
Olika material kräver olika kompressionsförhållande:
| Material | Rekommenderad kompression | Tillämpning |
|---|---|---|
| NBR (nitril) | 15-25% | Allmänt ändamål, oljebeständig |
| FKM (Viton) | 15-20% | Hög temperatur, kemisk beständighet |
| EPDM | 20-30% | Vatten- och ångtillämpningar |
| Silikon | 10-20% | Extrema temperaturintervall |
| PTFE | 5-10% | Kemikalieresistens, låg friktion |
Förra året arbetade jag med Michael, en underhållsingenjör på en livsmedelsfabrik i Wisconsin. Han upplevde ofta luftläckage i sina stånglösa cylindersystem trots att han använde O-ringar av högsta kvalitet. Efter att ha analyserat hans installation upptäckte jag att hans spårdesign orsakade överkompression (nästan 40%) av NBR O-ringarna.
Vi ändrade spårdimensionerna för att uppnå ett kompressionsförhållande på 20%, och tätningens livslängd förbättrades från 3 månader till över ett år, vilket sparade företaget tusentals kronor i underhållskostnader och stilleståndstid.
Miljöfaktorer som påverkar kompressionskraven
Det optimala kompressionsförhållandet är inte statiskt - det varierar beroende på:
- Temperaturfluktuationer: Högre temperaturer kräver lägre kompression för att ta hänsyn till värmeutvidgning
- Tryckskillnader: Högre tryck kan kräva högre kompression för att förhindra strängsprutning
- Dynamiska kontra statiska applikationer: Dynamiska tätningar behöver vanligtvis lägre kompression för att minska friktionen
- Installationsmetoder: Sträckning under installationen kan minska den effektiva kompressionen
Varför är Stribeck-kurvan viktig för design av pneumatiska tätningar?
Stribeck-kurvan kan låta akademisk, men den är faktiskt ett kraftfullt praktiskt verktyg för att förstå och optimera tätningsprestanda i stånglösa pneumatiska cylindrar och andra dynamiska applikationer.
Den Stribecks kurva3 illustrerar förhållandet mellan friktionskoefficient, smörjmedelsviskositet, hastighet och belastning i glidytor. I pneumatiska tätningar hjälper den ingenjörer att förstå övergången mellan gränssmörjning, blandad smörjning och hydrodynamisk smörjning, vilket är avgörande för att optimera tätningsdesignen för specifika driftsförhållanden.
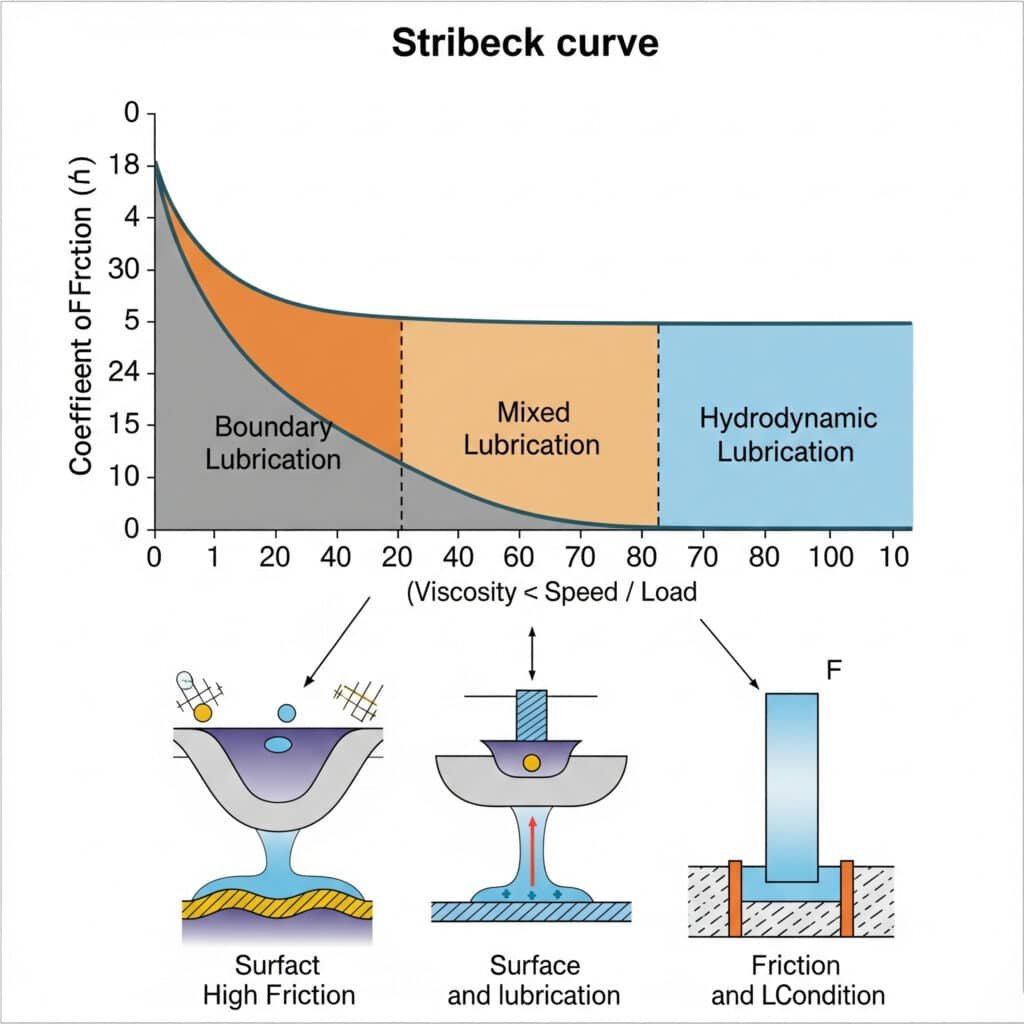
Att förstå denna kurva har praktiska konsekvenser för hur dina pneumatiska system fungerar i verkliga förhållanden.
De tre smörjregimerna i pneumatiska tätningar
Stribeck-kurvan identifierar tre distinkta driftregimer:
| Smörjningsregim | Egenskaper | Konsekvenser för pneumatiska tätningar |
|---|---|---|
| Gränssmörjning | Hög friktion, direkt ytkontakt | Uppstår under uppstart, låga hastigheter; orsakar stick-slip |
| Blandad smörjning | Måttlig friktion, delvis vätskefilm | Övergångszon; känslig för ytfinish och smörjmedel |
| Hydrodynamisk smörjning4 | Låg friktion, fullständig vätskeseparation | Idealisk för höghastighetsdrift; minimalt slitage |
Praktiska tillämpningar av Stribeck-kurvan vid val av tätning
Vid val av tätningar för stånglösa cylindrar är det bra att förstå Stribeck-kurvan:
- Anpassa tätningsmaterialet till driftförhållandena: Olika material fungerar bättre i olika smörjregimer
- Välj lämpliga smörjmedel: Kraven på viskositet ändras beroende på hastighet och belastning
- Utforma optimala ytbehandlingar: Grovhet påverkar övergången mellan smörjregimer
- Förutse och förhindra stick-slip-fenomen: Avgörande för smidig drift i precisionsapplikationer
Fallstudie: Eliminering av stick-slip vid precisionspositionering
Jag minns när jag arbetade med Emma, en automationsingenjör från en tillverkare av medicintekniska produkter i Schweiz. Hennes stånglösa cylindersystem upplevde ryckiga rörelser (stick-slip) under precisionsrörelser med låg hastighet, vilket påverkade produktkvaliteten.
Genom att analysera applikationen med hjälp av Stribeck-kurvan kom vi fram till att hennes system arbetade i gränssmörjningsregimen. Vi rekommenderade att man skulle byta till ett PTFE-baserat tätningsmaterial med modifierad ytstruktur och en annan smörjmedelsformulering.
Resultatet? Smidig rörelse även vid 5 mm/sekund, vilket eliminerar kvalitetsproblemen och förbättrar produktionsutbytet med 15%.
Vad orsakar friktionsuppvärmning i dynamiska tätningar och hur kan den kontrolleras?
Friktionsuppvärmning förbises ofta tills den orsakar förtida tätningsfel. Att förstå detta fenomen är viktigt för att kunna konstruera tillförlitliga pneumatiska system med lång livslängd.
Friktionsuppvärmning5 i dynamiska tätningar uppstår när mekanisk energi omvandlas till värmeenergi i kontaktytan mellan tätningen och anliggningsytan. Denna uppvärmning påverkas av faktorer som ythastighet, kontakttryck, smörjning och materialegenskaper. Överdriven uppvärmning påskyndar nedbrytningen av tätningen genom termisk nedbrytning av materialet.
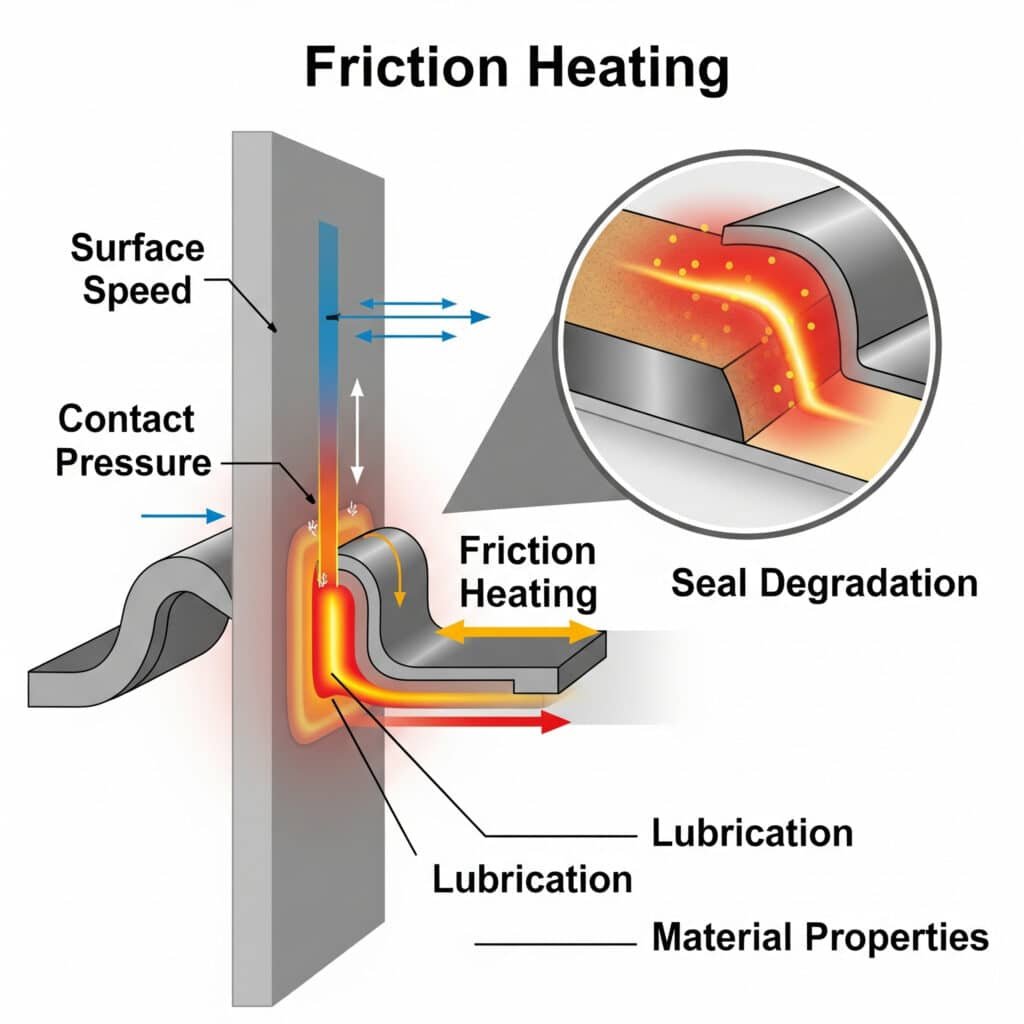
Konsekvenserna av friktionsuppvärmning kan vara allvarliga, från förkortad livslängd på tätningar till katastrofala fel. Låt oss utforska detta fenomen mer i detalj.
Kvantifiering av friktionsvärmeutveckling
Den värme som alstras genom friktion kan beräknas med hjälp av:
| Parameter | Formel | Exempel |
|---|---|---|
| Värmeproduktion (W) | Q = μ × F × v | För μ=0,2, F=100N, v=0,5m/s: Q = 0,2 × 100 × 0,5 = 10W |
| Temperaturökning (°C) | ΔT = Q/(m × c) | För 10W värme, 5g tätning, c=1,7J/g°C: ΔT = 10/(5 × 1,7) = 1,18°C/s |
| Temp vid stationärt tillstånd | Tss = Ta + (Q/hA) | Beror på värmeöverföringskoefficient och ytarea |
Var?
- μ = friktionskoefficient
- F = normalkraft
- v = glidhastighet
- m = massa
- c = specifik värmekapacitet
- Ta = omgivningstemperatur
- h = värmeöverföringskoefficient
- A = ytarea
Gränsvärden för kritisk temperatur för vanliga tätningsmaterial
Olika tätningsmaterial har olika temperaturgränser:
| Material | Maximal kontinuerlig temperatur (°C) | Tecken på termisk nedbrytning |
|---|---|---|
| NBR (nitril) | 100-120 | Härdning, sprickbildning, minskad elasticitet |
| FKM (Viton) | 200-250 | Missfärgning, minskad spänst |
| PTFE | 260 | Dimensionsförändringar, minskad draghållfasthet |
| TPU | 80-100 | Uppmjukning, deformation, missfärgning |
| UHMW-PE | 80-90 | Deformation, minskad slitstyrka |
Strategier för att minska friktionsvärmen
Baserat på min erfarenhet av applikationer med stånglösa cylindrar följer här några effektiva strategier för att kontrollera friktionsvärmen:
- Optimera kontakttrycket: Minska tätningsstörningar där så är möjligt utan att äventyra tätningen
- Förbättra smörjningen: Välj smörjmedel med lämplig viskositet och temperaturstabilitet
- Val av material: Välj material med lägre friktionskoefficienter och högre termisk stabilitet
- Ytbehandling: Ange lämplig ytfinish och beläggningar för att minska friktionen
- Design för värmeavledning: Inbyggda funktioner som förbättrar värmeöverföringen bort från tätningarna
Tillämpning i den verkliga världen: Konstruktion av stånglösa höghastighetscylindrar
En av våra kunder i Tyskland använder höghastighetsförpackningsutrustning med stånglösa cylindrar som körs i hastigheter upp till 2 m/s. Deras originaltätningar gick sönder efter bara 3 miljoner cykler på grund av friktionsuppvärmning.
Vi genomförde en termisk analys och upptäckte lokala temperaturer på upp till 140°C vid tätningsgränssnittet - långt över gränsen på 100°C för deras NBR-tätningar. Genom att byta till en PTFE-tätning i kompositmaterial med optimerad kontaktgeometri och förbättra cylinderns värmeavledning kunde vi förlänga tätningens livslängd till över 20 miljoner cykler.
Slutsats
Att förstå vetenskapen bakom O-ringars kompressionsförhållanden, Stribeck-kurvans praktiska tillämpningar och friktionsuppvärmningsmekanismer utgör grunden för att konstruera tillförlitliga, långlivade pneumatiska tätningssystem. Genom att tillämpa dessa principer kan du välja rätt tätningar för dina applikationer med stånglösa cylindrar, felsöka befintliga problem och förhindra kostsamma fel innan de uppstår.
Vanliga frågor om pneumatiska tätningsmekanismer
Vilket är det idealiska kompressionsförhållandet för O-ringar i pneumatiska applikationer?
Det idealiska kompressionsförhållandet för O-ringar i pneumatiska applikationer är normalt 15-25% för statiska tätningar och 10-20% för dynamiska tätningar. Detta intervall ger tillräcklig tätningskraft samtidigt som man undviker överdriven kompression som kan leda till förtida fel, särskilt i applikationer med stånglösa cylindrar.
Hur kan Stribeck-kurvan hjälpa mig att välja rätt tätning för min applikation?
Stribeck-kurvan hjälper till att identifiera vilken smörjregim din applikation kommer att arbeta i baserat på hastighet, belastning och smörjmedelsegenskaper. För applikationer med låga hastigheter och hög belastning ska du välja tätningar som är optimerade för gränssmörjning. För höghastighetsapplikationer ska du välja tätningar som är utformade för hydrodynamiska smörjförhållanden.
Vad orsakar stick-slip-rörelser i pneumatiska cylindrar och hur kan de förhindras?
Stick-slip-rörelse orsakas av skillnaden mellan statiska och dynamiska friktionskoefficienter, särskilt vid gränssmörjning. Förhindra det genom att använda PTFE-baserade eller andra tätningsmaterial med låg friktion, använda lämpliga smörjmedel, optimera ytfinishen och säkerställa korrekt tätningskompression för din stånglösa cylinderapplikation.
Hur stor temperaturökning kan accepteras för dynamiska tätningar?
Den acceptabla temperaturökningen beror på tätningsmaterialet. En allmän regel är att hålla driftstemperaturen minst 20°C under materialets maximala kontinuerliga temperaturklassning. För NBR-tätningar (nitril), som är vanliga i stånglösa cylindrar, bör temperaturen hållas under 80-100°C för längre livslängd.
Vad är förhållandet mellan tätningens hårdhet och kompressionskraven?
Hårdare tätningsmaterial (högre durometer) kräver normalt mindre kompression för att uppnå effektiv tätning. Till exempel kan ett 90 Shore A-material behöva endast 10-15% kompression, medan ett mjukare 70 Shore A-material kan behöva 20-25% kompression för samma tätningseffektivitet i pneumatiska applikationer.
Hur beräknar jag spårdimensionerna för en O-ringstätning?
Beräkna spårdimensionerna genom att bestämma det nödvändiga kompressionsförhållandet för din applikation och ditt material. För en standard 25%-komprimering av en 2,5 mm O-ring skulle spårdjupet vara 1,875 mm (2,5 mm × 0,75). Spårbredden bör tillåta 60-85% spårfyllnad för att möjliggöra kontrollerad deformation utan överdriven spänning.
-
Ger en grundläggande förklaring av elastomerer (polymerer med viskoelasticitet), som är de primära material som används för pneumatiska tätningar på grund av deras förmåga att deformeras och återgå till sin ursprungliga form. ↩
-
Erbjuder en teknisk definition av kompressionsuppsättning, den permanenta deformationen av en tätning efter långvarig tryckbelastning, vilket är en primär orsak till statisk tätningsfel. ↩
-
Redogör för principerna för Stribeck-kurvan, en grundläggande graf inom tribologi som illustrerar hur friktionen mellan två smorda ytor är en funktion av viskositet, belastning och hastighet. ↩
-
Förklarar hydrodynamisk smörjning, ett idealt tillstånd där en fullständig, kontinuerlig vätskefilm helt separerar två rörliga ytor, vilket resulterar i minimal friktion och slitage. ↩
-
Beskriver fysiken bakom friktionsuppvärmning, den process genom vilken mekanisk energi omvandlas till värmeenergi vid ett glidande gränssnitt, en kritisk faktor i den termiska nedbrytningen av dynamiska tätningar. ↩



