
Har du någonsin gått in på fabriksgolvet och mötts av det omisskännliga väsandet från pneumatiska system? Det ljudet är inte bara irriterande - det innebär slöseri med energi, potentiella problem med lagstiftningen och en varningssignal för ineffektiv drift.
Akustiskt buller i pneumatiska system genereras genom tre primära mekanismer: gasexpansion under tryckavlastning, mekanisk vibration av komponenter och turbulent flöde i rör och kopplingar. Genom att förstå dessa mekanismer kan ingenjörer implementera riktade bullerreduceringsstrategier som förbättrar säkerheten på arbetsplatsen, ökar energieffektiviteten och förlänger utrustningens livslängd.
Förra månaden besökte jag en läkemedelstillverkningsanläggning i New Jersey där överdrivet buller från deras stånglösa cylindrar orsakade problem med lagstiftningen. Deras team hade försökt med generiska lösningar utan framgång. Genom att analysera de specifika mekanismer som genererar buller minskade vi systembullret med 14 dBA - från att ha varit en risk för regelverket till att vara väl inom ramen för det. Låt mig visa dig hur vi gjorde det.
Innehållsförteckning
- Ljudnivå för gasexpansion: Vilken formel förutsäger pneumatiskt avgasljud?
- Mekaniskt vibrationsspektrum: Hur kan frekvensanalys identifiera bullerkällor?
- Ljuddämparens insättningsdämpning: Vilka beräkningar styr effektiv ljuddämpardesign?
- Slutsats
- Vanliga frågor om buller i pneumatiska system
Ljudnivå för gasexpansion: Vilken formel förutsäger pneumatiskt avgasljud?
Den plötsliga expansionen av tryckluft under ventilmanövrering eller cylinderutmatning skapar en av de mest betydande bullerkällorna i pneumatiska system. Att förstå det matematiska sambandet mellan systemparametrar och buller är avgörande för att effektivt kunna minska bullret.
Ljudeffektnivån från gasexpansion kan beräknas med hjälp av formeln: Lw = 10 log₁₀(W/W₀), där W är den akustiska effekten i watt och W₀ är referenseffekten (10-¹² watt). För pneumatiska system kan W beräknas som W = η × m × (c²/2), där η är den akustiska verkningsgraden, m är massflödet och c är gashastigheten.
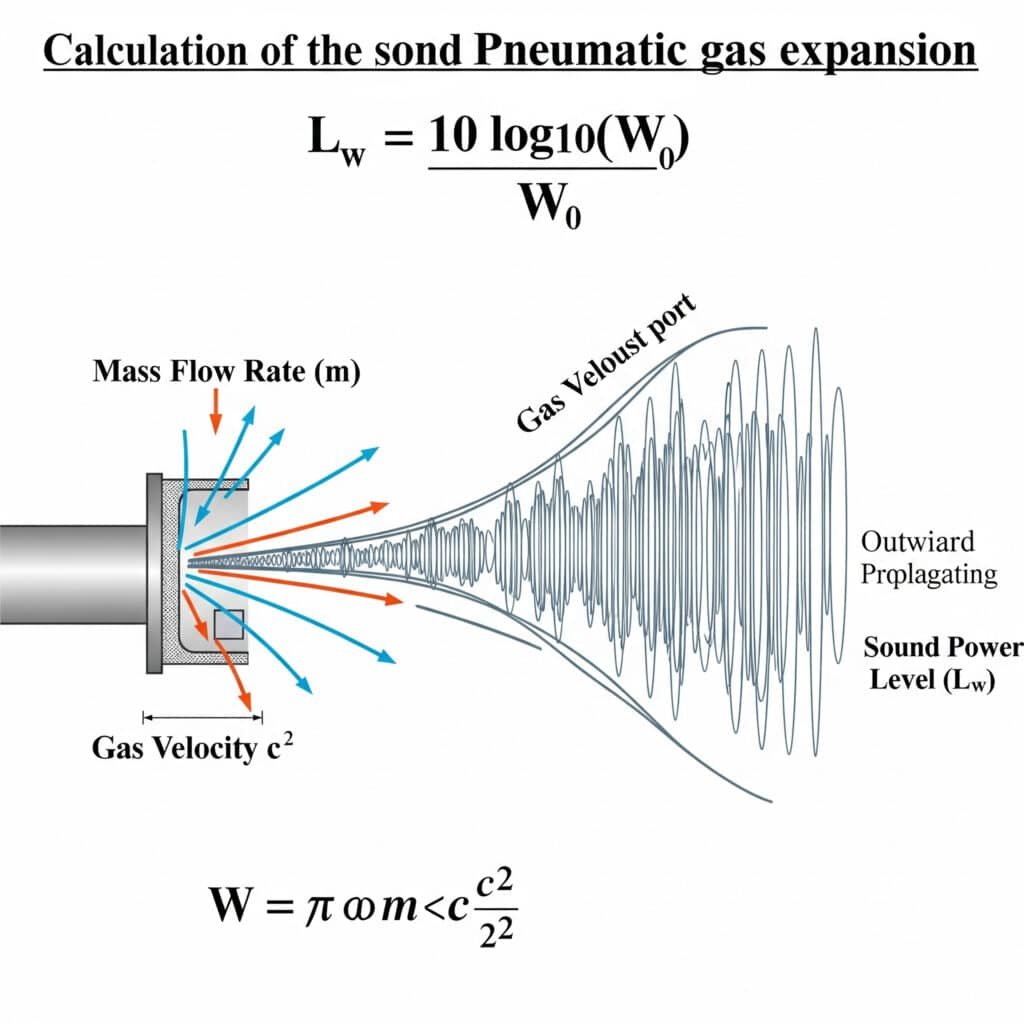
Jag minns en felsökning vid en förpackningslinje i Illinois där bullernivåerna översteg 95 dBA - långt över OSHA-gränser1. Underhållsteamet hade fokuserat på mekaniska källor, men vår analys visade att 70% av bullret kom från avgasportarna. Genom att tillämpa gasexpansionsformeln identifierade vi att drifttrycket var 2,2 bar högre än nödvändigt, vilket skapade ett överdrivet avgasljud. Denna enkla tryckjustering minskade bullret med 8 dBA utan att påverka prestandan.
Fundamentala ekvationer för gasexpansion och brus
Låt oss bryta ner de viktigaste formlerna för att förutsäga expansionsbuller:
Beräkning av ljudeffekt
Den akustiska effekt som alstras av expanderande gas kan beräknas enligt följande:
W = η × m × (c²/2)
Var?
- W = akustisk effekt (watt)
- η = akustisk verkningsgrad (typiskt 0,001-0,01 för pneumatiska utblås)
- m = Massflöde (kg/s)
- c = Gasens hastighet vid avgasröret (m/s)
Därefter anges ljudeffektnivån i decibel:
Lw = 10 log₁₀(W/W₀)
Där W₀ är referenseffekten på 10-¹² watt.
Bestämning av massflödeshastighet
Massflödet genom en öppning kan beräknas enligt följande:
m = Cd × A × p₁ × √(2γ/(γ-1) × (RT₁) × [(p₂/p₁)^(2/γ) - (p₂/p₁)^((γ+1)/γ)])
Var?
- Cd = Avtappningskoefficient (vanligtvis 0,6-0,8)
- A = Orifice-area (m²)
- p₁ = Absolut tryck uppströms (Pa)
- p₂ = Absolut tryck nedströms (Pa)
- γ = Specifik värmekvot (1,4 för luft)
- R = Gaskonstant för luft (287 J/kg-K)
- T₁ = Temperatur uppströms (K)
För strypt flöde (vanligt i pneumatiska utblås) förenklas detta till:
m = Cd × A × p₁ × √(γ/(RT₁)) × (2/(γ+1)) × (2/(γ+1))^((γ+1)/(2(γ-1))))
Faktorer som påverkar bullret från gasexpansion
| Faktor | Påverkan på bullernivån | Tillvägagångssätt för begränsning |
|---|---|---|
| Arbetstryck | 3-4 dBA ökning per bar | Sänk systemtrycket till lägsta nödvändiga nivå |
| Storlek på utloppsport | Mindre portar ökar hastigheten och bullret | Använd rätt dimensionerade portar för flödeskraven |
| Avgastemperatur | Högre temperaturer ökar bullret | Tillåt kylning före expansion där så är möjligt |
| Expansionsförhållande | Högre utväxling skapar mer buller | Stegvis expansion genom flera steg |
| Flödeshastighet | Fördubblat flöde ökar bullret med ~3 dBA | Använd flera mindre avgasrör i stället för ett stort |
Praktiskt exempel på bullerförutsägelse
För en typisk stångfri cylinder med:
- Arbetstryck: 6 bar (600.000 Pa)
- Avgasportens diameter: 4 mm (yta = 1,26 × 10-⁵ m²)
- Utsläppskoefficient: 0,7
- Akustisk effektivitet: 0,005
Massflödet under utblåsningen skulle vara ungefär:
m = 0,7 × 1,26 × 10-⁵ × 600 000 × 0,0404 = 0,0214 kg/s
Om man antar en utblåsningshastighet på 343 m/s (sonisk hastighet) blir den akustiska effekten
W = 0,005 × 0,0214 × (343²/2) = 6,29 watt
Den resulterande ljudeffektnivån:
Lw = 10 log₁₀(6,29/10-¹²) = 128 dB
Den höga ljudeffektnivån förklarar varför pneumatiska avgaser utan ljuddämpare är en så betydande bullerkälla i industriella miljöer.
Mekaniskt vibrationsspektrum: Hur kan frekvensanalys identifiera bullerkällor?
Mekaniska vibrationer i pneumatiska komponenter genererar distinkta ljudsignaturer som kan analyseras för att lokalisera specifika problem. Frekvensspektrumanalys är nyckeln till att identifiera och åtgärda dessa mekaniska bullerkällor.
Mekaniska vibrationer i pneumatiska system ger upphov till ljud med karakteristiska frekvensspektra som kan analyseras med hjälp av Snabb Fourier-transformation (FFT)2 tekniker. Viktiga frekvensområden omfattar lågfrekventa strukturella vibrationer (10-100 Hz), mellanfrekventa driftharmoniska (100-1000 Hz) och högfrekventa flödesinducerade vibrationer (1-10 kHz), som alla kräver olika metoder för att minska vibrationerna.
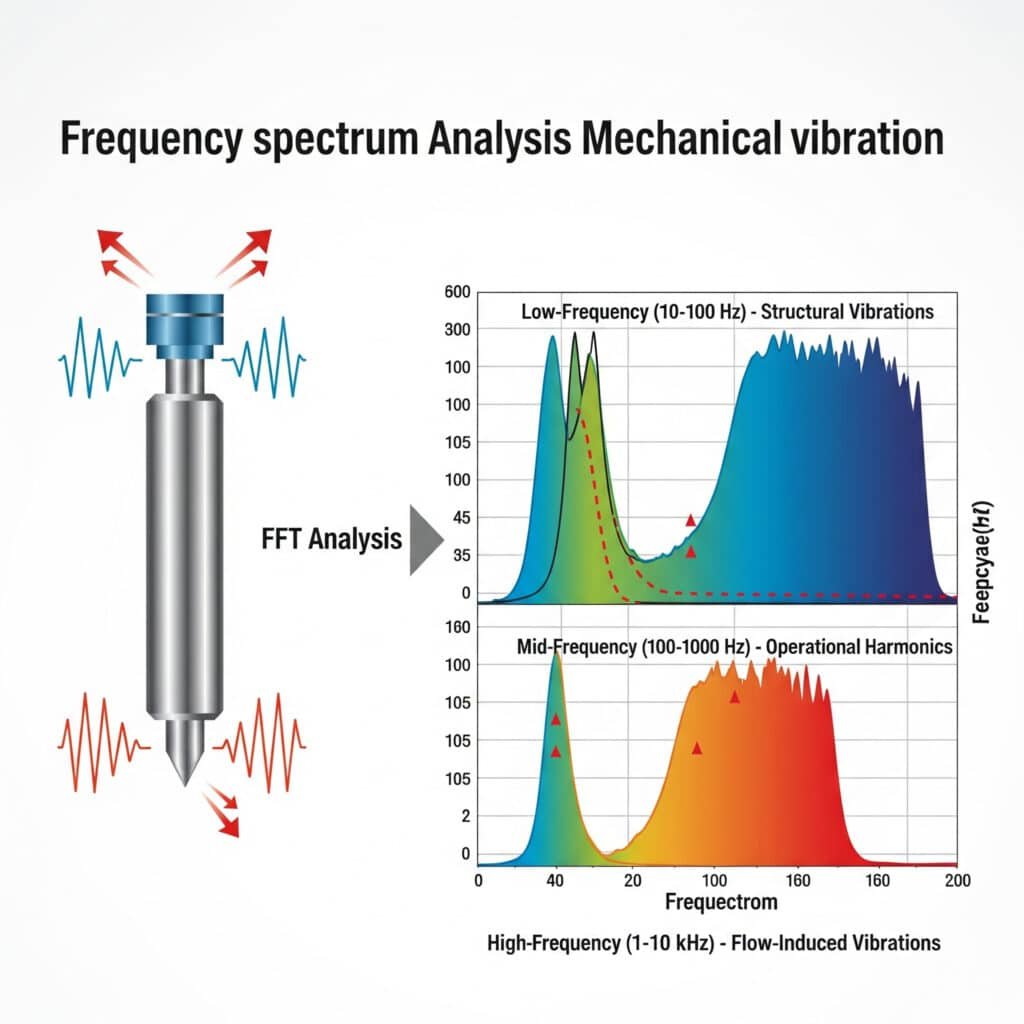
Under en konsultation hos en tillverkare av bildelar i Michigan hade deras underhållsteam problem med överdrivet buller från ett stånglöst cylinderöverföringssystem. Konventionell felsökning hade inte lyckats identifiera källan. Vår analys av vibrationsspektrumet visade en tydlig topp vid 237 Hz - vilket exakt motsvarar cylinderns interna tätningsbandresonans. Genom att modifiera monteringssystemet för att dämpa denna specifika frekvens minskade vi bullret med 11 dBA utan något produktionsavbrott.
Metodik för analys av frekvensspektrum
En effektiv vibrationsanalys följer ett systematiskt tillvägagångssätt:
- Inställning av mätning: Användning av accelerometrar och akustiska mikrofoner
- Datainsamling: Fånga upp vibrationssignaler i tidsdomänen
- FFT-analys: Konvertering till frekvensdomän
- Spektral kartläggning: Identifiering av karakteristiska frekvenser
- Källa Attribution: Matchning av frekvenser till specifika komponenter
Karakteristiska frekvensområden i pneumatiska system
| Frekvensområde | Typiska källor | Akustiska egenskaper |
|---|---|---|
| 10-50 Hz | Strukturell resonans, monteringsproblem | Lågfrekvent muller, känns mer än det hörs |
| 50-200 Hz | Kolvslag, aktivering av ventil | Tydligt dunkande eller knackande |
| 200-500 Hz | Friktion i tätning, intern resonans | Mittfrekvent surrande eller brummande |
| 500-2000 Hz | Flödesturbulens, tryckpulsationer | Väsande med tonala komponenter |
| 2-10 kHz | Läckage, höghastighetsflöde | Skarpt väsande, mest irriterande för det mänskliga örat |
| >10 kHz | Mikroturbulens, expansion av gas | Ultraljudskomponenter, indikator för energiförlust |
Överföringsvägar för vibrationer
Buller från mekaniska vibrationer följer flera vägar:
Strukturburen överföring
Vibrationer färdas genom solida komponenter:
- Komponent vibrerar på grund av inre krafter
- Vibrationsöverföring genom monteringspunkter
- Sammankopplade strukturer förstärker och utstrålar ljud
- Stora ytor fungerar som effektiva ljudradiatorer
Luftburen överföring
Direkt ljudstrålning från vibrerande ytor:
- Ytvibrationer förflyttar luft
- Förskjutning skapar tryckvågor
- Vågor sprids genom luften
- Strålningsytans storlek avgör verkningsgraden
Fallstudie: Vibrationsanalys för stånglösa cylindrar
För en magnetisk stångfri cylinder som uppvisar överdrivet buller:
| Frekvens (Hz) | Amplitud (dB) | Identifiering av källa | Strategi för begränsning |
|---|---|---|---|
| 43 | 78 | Montering av resonans | Förstärkt monteringsfäste |
| 86 | 65 | Harmonic av monteringsresonans | Adresseras med primär resonans |
| 237 | 91 | Resonans i tätningsband | Dämpningsmaterial har lagts till i cylinderkroppen |
| 474 | 83 | Harmonic av tätningsband | Adresseras med primär resonans |
| 1250 | 72 | Turbulens i luftflödet | Modifierad portdesign |
| 3700 | 68 | Läckage vid gavlar | Utbytta tätningar |
De kombinerade åtgärdsstrategierna minskade det totala bullret med 14 dBA, där den mest betydande förbättringen kom från att åtgärda 237 Hz-resonansen.
Avancerade tekniker för vibrationsanalys
Utöver den grundläggande FFT-analysen finns det flera avancerade tekniker som ger djupare insikter:
Orderanalys
Särskilt användbart för system med variabel hastighet:
- Spårar frekvenser som anpassas till drifthastigheten
- Separerar hastighetsberoende komponenter från komponenter med fast frekvens
- Identifierar problem relaterade till specifika rörelsefaser
Analys av operationell avböjningsform (ODS)
Kartlägger vibrationsmönster över hela systemet:
- Flera mätpunkter skapar en "karta" över vibrationer
- Avslöjar hur strukturer rör sig under drift
- Identifierar optimala platser för dämpande behandlingar
Modal analys
Bestämmer egenfrekvenser och modformer:
- Identifierar resonansfrekvenser före drift
- Förutser potentiella problemfrekvenser
- Vägleder till strukturella förändringar för att undvika resonans
Ljuddämparens insättningsdämpning: Vilka beräkningar styr effektiv ljuddämpardesign?
Ljuddämpare och ljuddämpare är avgörande för att minska bullret från pneumatiska system, men deras konstruktion måste baseras på sunda tekniska beräkningar för att säkerställa effektivitet utan att systemets prestanda äventyras.
Ljuddämpare insättningsförlust3 (IL) kvantifierar bullerdämpningens effektivitet och kan beräknas som IL = Lw₁ - Lw₂, där Lw₁ är ljudeffektnivån utan ljuddämparen och Lw₂ är nivån med ljuddämparen installerad. För pneumatiska system uppnår effektiva ljuddämpare vanligtvis 15-30 dB insättningsdämpning över det kritiska frekvensområdet 500 Hz till 4 kHz samtidigt som de upprätthåller ett acceptabelt mottryck.
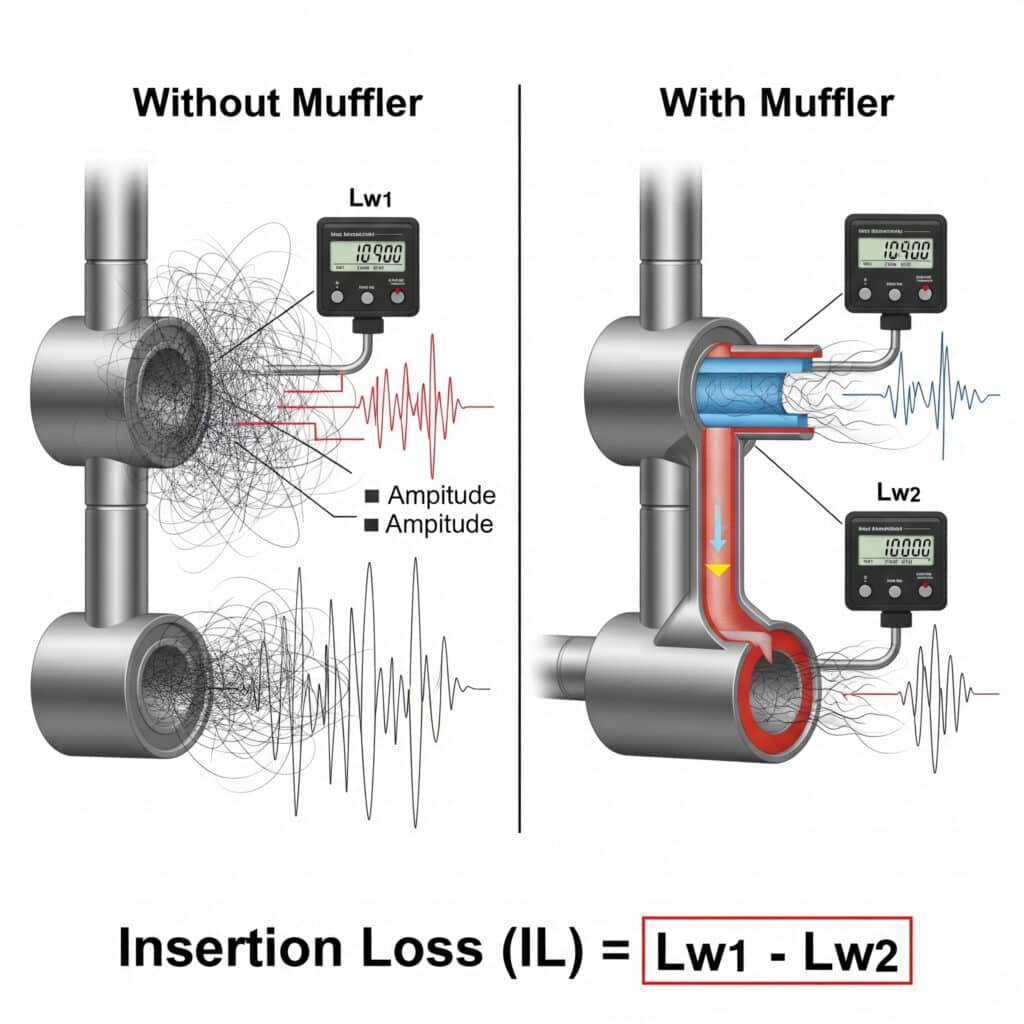
Jag hjälpte nyligen en tillverkare av medicintekniska produkter i Massachusetts att lösa ett utmanande bullerproblem med sitt stånglösa precisionscylindersystem. Deras första försök att använda ljuddämpare från hyllan minskade bullret men skapade ett alltför högt mottryck som påverkade cykeltiderna. Genom att beräkna den nödvändiga insättningsdämpningen för specifika frekvensband och konstruera en anpassad ljuddämpare med flera kammare uppnådde vi en ljudreduktion på 24 dB med minimal påverkan på prestandan. Resultatet blev ett system som uppfyllde både ljud- och precisionskraven.
Grundläggande om ljuddämpares inkopplingsförlust
Kärnekvationen för insättningsförlust är:
IL = Lw₁ - Lw₂
Var?
- IL = inkopplingsförlust (dB)
- Lw₁ = Ljudeffektnivå utan ljuddämpare (dB)
- Lw₂ = Ljudeffektnivå med ljuddämpare (dB)
För frekvensspecifik analys blir detta:
IL(f) = Lw₁(f) - Lw₂(f)
Där f anger det specifika frekvensband som analyseras.
Ljuddämparens konstruktionsparametrar och deras effekter
| Parameter | Effekt på inkopplingsförlust | Effekt på mottryck | Optimalt intervall |
|---|---|---|---|
| Kammarens volym | Större volym ökar lågfrekvent IL | Minimal påverkan om den utformas på rätt sätt | 10-30× avgasportens volym |
| Antal kammare | Fler kammare ökar mellanfrekvensen IL | Ökar med fler kammare | 2-4 kammare för de flesta applikationer |
| Expansionsförhållande | Högre kvot förbättrar IL | Minimal påverkan om den sker gradvis | 4:1 till 16:1 ytförhållande |
| Akustiskt material | Förbättrar högfrekvent IL | Minimal påverkan med rätt design | 10-50 mm tjocklek |
| Perforering av baffel | Påverkar mellanfrekvensen IL | Betydande inverkan | 30-50% öppen yta |
| Flödesvägens längd | Längre banor förbättrar lågfrekvent IL | Ökar med längden | 3-10× portdiameter |
Teoretiska modeller för prediktering av inkopplingsförlust
Flera modeller kan förutsäga insättningsdämpningen för olika ljuddämpartyper:
Expansionskammare Modell
För enkla expansionskammare:
IL = 10 log₁₀[1 + 0,25(m-1/m)² sin²(kL)]
Var?
- m = ytförhållande (kammarens area / rörets area)
- k = vågtal (2πf/c, där f är frekvens och c är ljudhastighet)
- L = kammarens längd
Modell av avledande ljuddämpare
För ljuddämpare med ljudabsorberande material:
IL = 8,68α(L/d)
Var?
- α = Absorptionskoefficient för materialet
- L = Längd på den fodrade sektionen
- d = flödesvägens diameter
Reaktiv modell för ljuddämpare (Helmholtz-resonator4)
För ljuddämpare av resonatortyp:
IL = 10 log₁₀[1 + (ρc/2S)² × (V/L'c²) × ω²/((ω₀² - ω²)² + (Rω/ρc)²)]
Var?
- ρ = luftens densitet
- c = ljudets hastighet
- S = Halsens tvärsnittsarea
- V = Kavitetens volym
- L' = effektiv halslängd
- ω = Vinkelfrekvens
- ω₀ = Resonansfrekvens
- R = akustiskt motstånd
Praktisk process för val av ljuddämpare
Att välja eller konstruera en lämplig ljuddämpare:
- Mät brusspektrum: Bestäm frekvensinnehållet i bullret
- Beräkna erforderlig IL: Bestäm nödvändig minskning av frekvensen
- Bedömning av flödeskrav: Beräkna maximalt tillåtet mottryck
- Välj typ av ljuddämpare:
- Reaktiv (expansionskammare) för låga frekvenser
- Dissipativ (absorberande) för höga frekvenser
- Kombination för bredbandsbuller - Verifiera prestanda: Test av insättningsförlust och mottryck
Överväganden om mottryck
För högt mottryck kan påverka systemets prestanda avsevärt:
Beräkning av mottryck
Baktrycket kan beräknas som:
ΔP = ρ(Q/Cd×A)²/2
Var?
- ΔP = Tryckfall (Pa)
- ρ = luftens densitet (kg/m³)
- Q = Flödeshastighet (m³/s)
- Cd = Utsläppskoefficient
- A = Effektiv flödesarea (m²)
Konsekvensbedömning av prestationer
För en stånglös cylinder med:
- Borrdiameter: 40 mm
- Slaglängd: 500 mm
- Cykeltid: 2 sekunder
- Arbetstryck: 6 bar
Varje 0,1 bar av mottryck skulle:
- Minska kraftuttaget med cirka 1,7%
- Öka cykeltiden med cirka 2,3%
- Öka energiförbrukningen med cirka 1,5%
Fallstudie: Anpassad ljuddämpardesign
För en precisionsapplikation med en stånglös cylinder med strikta ljudkrav:
| Parameter | Initialt tillstånd | Ljuddämpare från hyllan | Anpassad design |
|---|---|---|---|
| Ljudnivå | 89 dBA | 76 dBA | 65 dBA |
| Bakåtsträvande | 0,05 bar | 0,42 bar | 0,11 bar |
| Cykeltid | 1,8 sekunder | 2,3 sekunder | 1,9 sekunder |
| Frekvenssvar | Bredband | Dålig vid 2-4 kHz | Optimerad över hela spektrumet |
| Livslängd | N/A | 3 månader (igensättning) | >12 månader |
| Kostnad för implementering | N/A | $120 per punkt | $280 per punkt |
Den specialdesignade ljuddämparen gav överlägsen bullerdämpning med bibehållen acceptabel systemprestanda, med en återbetalningstid på mindre än 6 månader om man räknar med produktivitetsförbättringar.
Slutsats
Förståelse för mekanismerna bakom akustisk bullergenerering - ljudnivåer vid gasexpansion, mekaniska vibrationsspektra och beräkningar av ljuddämparens insättningsdämpning - utgör grunden för effektiv bullerkontroll i pneumatiska system. Genom att tillämpa dessa principer kan du skapa tystare, effektivare och mer tillförlitliga pneumatiska system samtidigt som du säkerställer efterlevnad av regler och förbättrar förhållandena på arbetsplatsen.
Vanliga frågor om buller i pneumatiska system
Vilka är OSHA:s gränsvärden för exponering för buller från pneumatiska system?
OSHA begränsar bullerexponeringen på arbetsplatsen till 90 dBA för ett tidsvägt genomsnitt på 8 timmar, med en växelkurs på 5 dBA. NIOSH:s rekommenderade gränsvärde för exponering är dock mer konservativt och ligger på 85 dBA. Pneumatiska system överskrider ofta dessa gränsvärden, med ljudlösa avgaser som ofta genererar 90-110 dBA på en meters avstånd, vilket kräver tekniska kontroller för efterlevnad.
Hur påverkar arbetstrycket ljudet i ett pneumatiskt system?
Drifttrycket har en betydande inverkan på bullergenereringen, där varje ökning av trycket med 1 bar normalt ökar avgasbullernivån med 3-4 dBA. Detta förhållande är logaritmiskt snarare än linjärt, eftersom ljudeffekten ökar med kvadraten på tryckförhållandet. Att sänka systemtrycket till det minimum som krävs för driften är ofta den enklaste och mest kostnadseffektiva strategin för att minska bullret.
Vad är skillnaden mellan reaktiva och dissipativa ljuddämpare för pneumatiska system?
Reaktiva ljuddämpare använder kammare och passager för att reflektera ljudvågor och skapa destruktiv interferens, vilket gör dem effektiva för lågfrekvent buller (under 500 Hz) med minimalt tryckfall. Dissipativa ljuddämpare använder ljudabsorberande material för att omvandla akustisk energi till värme, vilket gör dem mer effektiva för högfrekvent buller (över 500 Hz) men mer känsliga för föroreningar. Många industriella pneumatiska ljuddämpare kombinerar båda principerna för bredbandig bullerdämpning.
Hur kan jag identifiera den dominerande bullerkällan i mitt pneumatiska system?
Använd ett systematiskt tillvägagångssätt som börjar med drifttestning: kör systemet vid olika tryck, hastigheter och belastningar samtidigt som du mäter bullret. Utför sedan komponentisolering genom att använda enskilda element separat. Slutligen ska du göra en frekvensanalys med hjälp av en ljudnivåmätare med oktavbandskapacitet - låga frekvenser (50-250 Hz) indikerar vanligtvis strukturella problem, mellanfrekvenser (250-2000 Hz) tyder på driftsbuller och höga frekvenser (2-10 kHz) pekar på flödes- eller läckageproblem.
Vad är sambandet mellan ljudnivå och avstånd från en pneumatisk komponent?
Buller från pneumatiska komponenter följer den omvända kvadratiska lagen i frifältsförhållanden och minskar med cirka 6 dB varje gång avståndet fördubblas. Men i typiska industrimiljöer med reflekterande ytor är den faktiska minskningen ofta bara 3-4 dB per fördubbling av avståndet på grund av efterklang. Det innebär att en fördubbling av avståndet från en bullerkälla på 90 dB kanske bara sänker nivån till 86-87 dB i stället för de teoretiska 84 dB.
-
Ger de officiella OSHA-bestämmelserna (Occupational Safety and Health Administration) och tillåtna exponeringsgränser (PEL) för buller på arbetsplatsen, vilket är en viktig drivkraft för akustisk dämpning. ↩
-
Förklarar FFT-algoritmen (Fast Fourier Transform), ett viktigt matematiskt verktyg som används för att omvandla en tidsdomänsignal (t.ex. en vibration eller ljudvåg) till dess ingående frekvenskomponenter för analys. ↩
-
Beskriver modalanalys, en avancerad ingenjörsteknik som används för att bestämma ett systems inneboende dynamiska egenskaper, t.ex. dess egenfrekvenser och modformer, för att förutsäga och undvika resonans. ↩
-
Ger en detaljerad förklaring av Insertion Loss (IL), det primära mått som används för att kvantifiera prestandan hos en ljuddämpare genom att mäta den ljudnivåreduktion som den ger. ↩



