Kämpar du med långsamma cylinderhastigheter, inkonsekventa rörelser eller otillräcklig kraft i dina pneumatiska system? Dessa vanliga problem beror ofta på en missförstådd orsak: flödesmotstånd. Många ingenjörer dimensionerar sina pneumatiska komponenter enbart utifrån tryck- och kraftkrav och bortser från flödesmotståndets avgörande inverkan på prestandan i den verkliga världen.
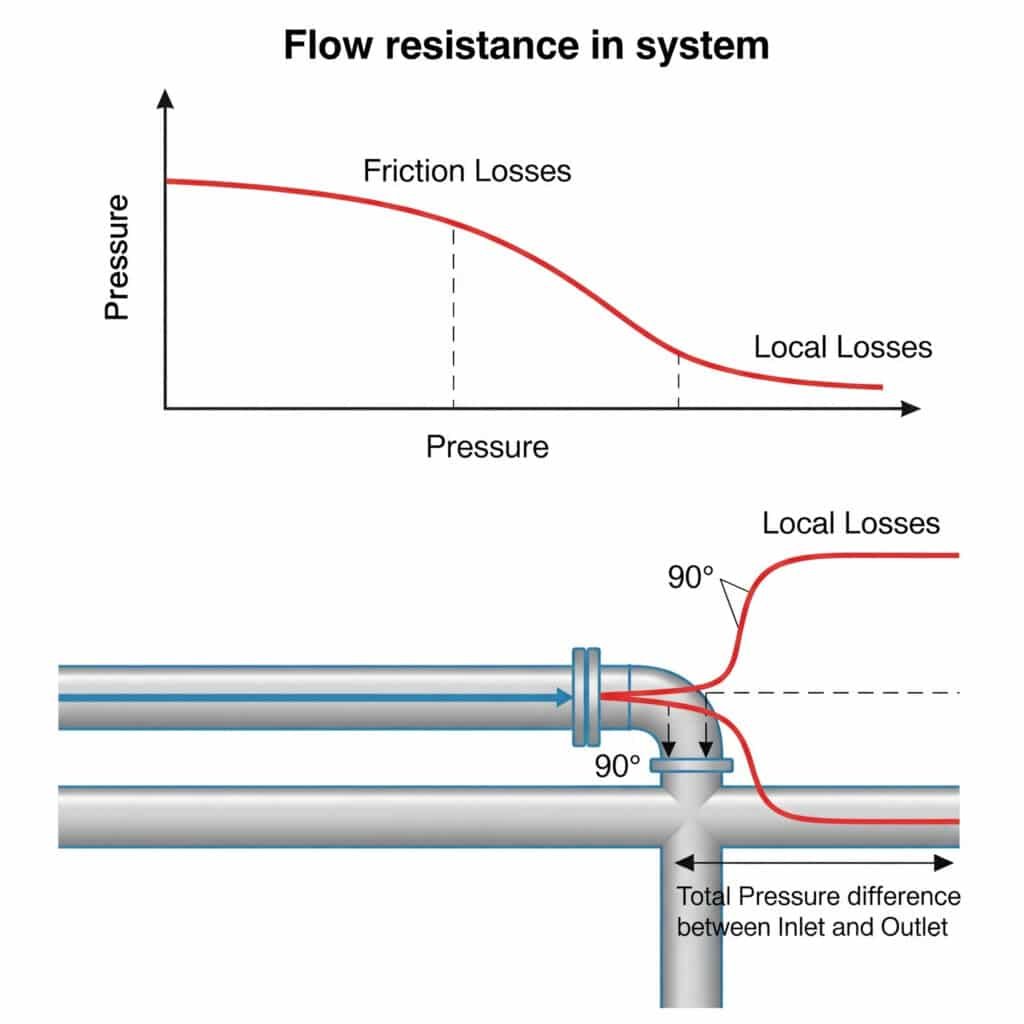
Flödesmotstånd i pneumatiska system skapar tryckfall som minskar den tillgängliga kraften, begränsar maxhastigheten och orsakar ojämn rörelse. Detta motstånd kommer från både friktion längs raka rör (friktionsförluster) och störningar vid kopplingar, böjar och ventiler (lokala förluster). Tillsammans kan dessa motstånd minska den faktiska systemprestandan med 20-50% jämfört med teoretiska beräkningar.
Under mina mer än 15 år på Bepto, där jag arbetat med pneumatiska system, har jag sett otaliga fall där förståelse för och hantering av flödesmotstånd har förvandlat underpresterande system till tillförlitliga och effektiva verksamheter. Låt mig dela med mig av vad jag har lärt mig om att beräkna och minimera dessa dolda prestandadödare.
Innehållsförteckning
- Hur beräknar man egentligen friktionsförluster i pneumatiska ledningar?
- Varför är metoden med ekvivalent längd så viktig för korrekt systemdesign?
- Vad händer när luft strömmar genom sektioner med reducerat borrhål?
- Slutsats
- Vanliga frågor om flödesmotstånd i pneumatiska system
Hur beräknar man egentligen friktionsförluster i pneumatiska ledningar?
Friktionsförluster i raka rör är grunden för beräkningar av flödesmotstånd, men många ingenjörer förlitar sig på alltför förenklade tumregler som leder till underdimensionerade system.
Friktionsförluster i pneumatiska ledningar beräknas med hjälp av Darcy-Weisbach-ekvationen1: ΔP = λ(L/D)(ρv²/2), där λ är friktionsfaktorn, L är rörlängden, D är rördiametern, ρ är luftdensiteten och v är flödeshastigheten. För pneumatiska system varierar friktionsfaktorn λ baserat på Reynolds tal2 och relativ grovhet, och bestäms vanligtvis med hjälp av uppslagstabeller eller Moody-diagram3.
Att förstå friktionsförluster har praktiska konsekvenser för systemdesign och felsökning. Låt mig bryta ner detta till användbara insikter.
Effektiv användning av friktionsfaktortabeller
Friktionsfaktorn (λ) är den viktigaste parametern vid beräkning av tryckfall, men för att bestämma dess värde måste man ta hänsyn till flödesförhållandena:
| Flödesregim | Reynolds tal (Re) | Bestämning av friktionsfaktor |
|---|---|---|
| Laminärt flöde | Re < 2000 | λ = 64/Re |
| Övergångsflöde | 2000 < Re < 4000 | Opålitlig - undvik att designa i detta intervall |
| Turbulent flöde | Re > 4000 | Använd uppslagstabeller baserade på relativ grovhet (ε/D) |
Uppslagstabell för praktisk friktionsfaktor
För turbulent flöde i pneumatiska system, använd denna förenklade tabell:
| Rörmaterial | Relativ ojämnhet (ε/D) | Friktionsfaktor (λ) vid vanliga Reynolds tal |
|---|---|---|
| Re = 10.000 | ||
| Släta slangar (PVC, polyuretan) | 0.0001 – 0.0005 | 0.031 |
| Aluminiumrör | 0.001 – 0.002 | 0.035 |
| Galvaniserat stål | 0.003 – 0.005 | 0.042 |
| Rostat stål | 0.01 – 0.05 | 0.054 |
Beräkning av tryckfall i verkliga pneumatiska system
Låt oss gå igenom ett praktiskt exempel:
| Parameter | Värde/beräkning | Exempel |
|---|---|---|
| Rörets diameter (D) | Invändig diameter | 8 mm (0,008 m) |
| Rörets längd (L) | Total rak längd | 5m |
| Flödeshastighet (Q) | Från systemkrav | 20 standardliter/sekund |
| Luftens densitet (ρ) | Vid arbetstryck | 7,2 kg/m³ vid 6 bar |
| Flödeshastighet (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Reynolds tal (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1.273.600 |
| Relativ grovhet | För polyuretanslangar | 0.0003 |
| Friktionsfaktor (λ) | Från uppslagstabell | 0.017 |
| Tryckfall (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Tillämpning i den verkliga världen: Lösning av problem med cylinderhastigheten
Förra året arbetade jag med Sarah, en tillverkningsingenjör på ett företag som tillverkar förpackningsutrustning i Wisconsin. Hennes stånglösa cylindersystem arbetade med endast 60% av den förväntade hastigheten, trots att det hade rätt cylinderstorlek och tillräckligt matningstryck.
Efter att ha analyserat hennes system upptäckte jag att hon använde 6 mm slangar för en högflödesapplikation. Friktionsförlusterna orsakade ett tryckfall på 2,1 bar, vilket avsevärt minskade den tillgängliga kraften och hastigheten. Genom att uppgradera till 10 mm slang minskade vi tryckfallet till 0,4 bar, och hennes system uppnådde omedelbart den prestanda som krävdes utan några andra förändringar.
Faktorer som påverkar friktionsförluster i verkliga system
Flera faktorer påverkar de faktiska friktionsförlusterna:
- Lufttemperatur: Högre temperaturer ökar viskositeten och friktionen
- Kontaminering: Smuts och olja kan öka den effektiva ojämnheten
- Bockning av rör: Mikrodeformation i böjda rör ökar motståndskraften
- Försämring på grund av ålder: Korrosion och avlagringar ökar ojämnheten över tid
- Arbetstryck: Högre tryck ökar densiteten och förlusterna
Varför är metoden med ekvivalent längd så viktig för korrekt systemdesign?
Lokala förluster vid kopplingar, ventiler och böjar överstiger ofta friktionsförlusterna i raka rör, men många ingenjörer ignorerar dem eller använder grova uppskattningsmetoder som leder till prestandaproblem.
Metoden med ekvivalent längd omvandlar lokala förluster från kopplingar och ventiler till en ekvivalent längd av rakt rör som skulle orsaka samma tryckfall. Detta beräknas med Le = K(D/λ), där Le är den ekvivalenta längden, K är lokal förlustkoefficient4, D är rördiametern och λ är friktionsfaktorn. Denna metod förenklar beräkningarna och ger mer exakta förutsägelser av systemets prestanda.
Låt oss utforska hur man kan tillämpa denna metod effektivt vid konstruktion av pneumatiska system.
Tabeller för ekvivalenta längder för vanliga pneumatiska komponenter
Här är en praktisk referenstabell för vanliga pneumatiska komponenter:
| Komponent | K-värde | Ekvivalent längd (Le/D) |
|---|---|---|
| 90° armbåge (skarp) | 0.9 | 30 |
| 90° armbåge (standardradie) | 0.3 | 10 |
| 45° krök | 0.2 | 7 |
| T-Junction (genomgående flöde) | 0.3 | 10 |
| T-korsning (grenflöde) | 1.0 | 33 |
| Kulventil (helt öppen) | 0.1 | 3 |
| Avstängningsventil (helt öppen) | 0.2 | 7 |
| Snabbkoppling för anslutning | 0.4-0.8 | 13-27 |
| Backventil | 1.5-2.5 | 50-83 |
| Standard flödesreglerventil | 1.0-3.0 | 33-100 |
Tillämpning av metoden för ekvivalent längd
För att använda denna metod effektivt:
- Identifiera alla komponenter i din pneumatiska krets
- Hitta K-värdet eller det ekvivalenta längdförhållandet (Le/D) för varje komponent
- Beräkna den ekvivalenta längden genom att multiplicera med rördiametern
- Lägg till alla motsvarande längder till den faktiska längden på det raka röret
- Använd den totala effektiva längden i dina beräkningar av friktionsförlust
Till exempel ett system med 5 m rak 8 mm slang plus fyra 90° böjar, en T-koppling och två snabbkopplingar:
| Komponent | Kvantitet | Le/D | Ekvivalent längd |
|---|---|---|---|
| 90° armbågar | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| T-korsning | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Snabbkopplingar | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Total ekvivalent längd | 0.72m | ||
| Faktisk rak längd | 5.00m | ||
| Total effektiv längd | 5.72m |
Detta innebär att ditt 5 m-system faktiskt beter sig som ett 5,72 m-system på grund av lokala förluster - en ökning av den effektiva längden med 14,4%.
Fallstudie: Optimering av ventilplacering i monteringssystem
Jag hjälpte nyligen Miguel, en automationsingenjör på en fabrik för elektronikmontering i Arizona. Hans pick-and-place-system hade inkonsekventa rörelser och cykeltidsvariationer, trots att det använde komponenter av hög kvalitet.
Analysen visade att hans ventilfördelare var placerad 3 m från cylindrarna och att kretsen innehöll många kopplingar. Beräkningen av ekvivalent längd visade att det faktiska avståndet på 3 m hade en effektiv längd på 7,2 m på grund av lokala förluster - mer än dubbelt så långt som avståndet med raka rör!
Genom att flytta ventilgrenröret närmare cylindrarna och ta bort flera kopplingar minskade vi den effektiva längden från 7,2 m till 2,1 m. Detta minskade tryckfallet med 70%, vilket resulterade i en jämn rörelse och en minskning av cykeltiden med 15%.
Praktiska tips för att minimera lokala förluster
För att minska lokala förluster i dina pneumatiska system:
- Använd svängda eller rundade armbågar i stället för skarpa böjar (minskar K-värdet med 67%)
- Minimera antalet beslag genom att planera mer direkta rutter
- Välj komponenter med låg friktion som fullborrade kulventiler där så är lämpligt
- Dimensionera kopplingar korrekt - underdimensionerade rördelar orsakar oproportionerliga förluster
- Placera ventilerna nära ställdonen för att minimera den effektiva slanglängden
Vad händer när luft strömmar genom sektioner med reducerat borrhål?
Reducerade borrhål i pneumatiska kretsar - t.ex. delvis stängda ventiler, underdimensionerade kopplingar eller diameterövergångar - skapar betydande flödesbegränsningar som allvarligt kan påverka systemets prestanda.
När luft strömmar genom reducerade hålsektioner, tryckfall5 uppstår enligt formeln ΔP = ρ(v₂² - v₁²)/2, där v₁ är hastigheten före förträngningen och v₂ är hastigheten i förträngningen. Detta kan kompenseras med hjälp av kompensationsfaktorn för borrförhållandet C = (1 - (d/D)⁴), där d är den reducerade diametern och D är den ursprungliga diametern. Denna faktor hjälper till att förutsäga systemets faktiska prestanda och undvika underdimensionering av komponenter.
Låt oss undersöka de praktiska konsekvenserna av reducerade borrsnitt och hur man tar hänsyn till dem i systemdesignen.
Beräkning av tryckfall vid diameterövergångar
När luft strömmar från en större diameter till en mindre kan tryckfallet beräknas med hjälp av:
| Parameter | Formel | Exempel |
|---|---|---|
| Ursprunglig diameter (D) | Från specifikationer | 10 mm |
| Reducerad diameter (d) | Från specifikationer | 6 mm |
| Borrningsförhållande (d/D) | Enkel uppdelning | 0.6 |
| Flödeshastighet (Q) | Från systemkrav | 15 standard liter/sekund |
| Hastighet i originalröret (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Hastighet i reducerad sektion (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Tryckfall (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Kompensationsfaktor (C) | C = (1 - (d/D)⁴) | 0.87 |
Vanliga scenarier för borrhålsreduktion och deras inverkan
Så här påverkar olika borrhålsreduktioner flödeskapaciteten:
| Borrhålsreduktion | Minskning av flödeskapaciteten | Ökning av tryckfall |
|---|---|---|
| 10 mm till 8 mm | 36% | 2.4× |
| 10 mm till 6 mm | 64% | 7.7× |
| 10 mm till 4 mm | 84% | 39× |
| 8mm till 6mm | 44% | 3.2× |
| 8 mm till 4 mm | 75% | 16× |
| 6 mm till 4 mm | 56% | 5.1× |
Dessa siffror belyser varför till synes små minskningar av diametern kan ha dramatiska effekter på systemets prestanda.
Den kumulativa effekten av flera begränsningar
I verkliga pneumatiska kretsar förekommer flera begränsningar i serie. Deras effekt är kumulativ och kan beräknas med hjälp av:
- Omvandla varje restriktion till dess motsvarande C-faktor
- Beräkna den totala C-faktorn: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Använd denna totala faktor för att bestämma den totala prestandareduktionen för systemet
Fallstudie: Lösning av problem med felmatchning mellan ventil och ställdon
Förra månaden arbetade jag med Thomas, en underhållschef på en möbelfabrik i North Carolina. Hans nya stånglösa cylindersystem arbetade med mindre än hälften av den förväntade hastigheten, trots att han använde tillverkarens rekommenderade ventilstorlek.
Undersökningen avslöjade flera borrhålsreduceringar i hans krets:
- 10 mm matarledning till 8 mm ventilportar (C₁ = 0,36)
- 8 mm ventilportar till 6 mm kopplingar (C₂ = 0,44)
- 6 mm kopplingar till 8 mm cylinderportar med interna begränsningar (C₃ = 0,32)
Den totala kompensationsfaktorn var Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, vilket innebär att hans system förlorade 75% av sin teoretiska flödeskapacitet!
Genom att uppgradera till rätt dimensionerade komponenter i hela systemet eliminerade vi dessa begränsningar och uppnådde önskad prestanda utan att ändra cylinder eller matningstryck.
Praktiska strategier för att minimera förlusterna vid borrhålsreduktion
För att minska förluster från borrhålsreduktioner:
- Storleken på komponenterna är konsekvent i hela den pneumatiska kretsen
- Använd den största praktiska slangstorleken för applikationer med högt flöde
- Var uppmärksam på begränsningar för interna komponenter, inte bara anslutningsstorlekar
- Överväg parallella flödesvägar för krav på höga flöden
- Eliminera onödiga adaptrar och övergångar när så är möjligt
Principen om "den svagaste länken" i pneumatiska system
Kom ihåg att ditt pneumatiska systems prestanda begränsas av dess mest restriktiva komponent. Ett enda underdimensionerat element kan upphäva fördelarna med korrekt dimensionerade komponenter på andra ställen i systemet.
Till exempel kommer ett system med 10 mm slangar, 10 mm ventiler men 6 mm kopplingar vid cylindern att ha i princip samma prestanda som ett system med 6 mm komponenter genomgående - men till en högre kostnad.
Slutsats
Att förstå och korrekt beräkna flödesmotstånd - genom friktionsfaktortabeller, metoder för ekvivalent längd och kompensation för reducerat hål - är avgörande för att utforma pneumatiska system som fungerar som förväntat under verkliga förhållanden. Genom att tillämpa dessa beräkningsmetoder och konstruktionsprinciper kan du optimera dina applikationer med stånglösa cylindrar och andra pneumatiska system för maximal prestanda och tillförlitlighet.
Vanliga frågor om flödesmotstånd i pneumatiska system
Hur stort tryckfall kan accepteras i ett pneumatiskt system?
Det acceptabla tryckfallet beror på applikationskraven, men som en allmän riktlinje bör det totala tryckfallet begränsas till 10-15% av matningstrycket för effektiv drift. För ett 6 bar-system innebär detta att det totala tryckfallet måste hållas under 0,6-0,9 bar. Kritiska applikationer kan kräva ännu lägre tryckfall på 5-8% för att bibehålla konsekvent prestanda.
Vad är sambandet mellan rördiameter och tryckfall?
Tryckfallet är omvänt proportionellt mot femte potensen av diametern (D⁵) för turbulent flöde i pneumatiska system. Det innebär att en fördubbling av rördiametern minskar tryckfallet med cirka 32 gånger. Till exempel kan en ökning från 6 mm till 12 mm slang minska tryckfallet från 1,5 bar till bara 0,047 bar under samma flödesförhållanden.
Hur bestämmer jag rätt slangstorlek för min pneumatiska applikation?
Välj rörstorlek utifrån krav på flödeshastighet och acceptabelt tryckfall. Beräkna Reynolds tal och friktionsfaktor och använd sedan Darcy-Weisbach-ekvationen för att bestämma tryckfallet för olika diametrar. Välj den minsta diametern som håller tryckfallet inom acceptabla gränser (vanligtvis <10% av matningstrycket) samtidigt som hänsyn tas till utrymmesbegränsningar och kostnad.
Vad skapar störst begränsning: en 90°-vinkel eller 5 meter rak slang?
En skarp 90°-vinkel skapar vanligtvis ett motstånd som motsvarar 30 rördiametrar av raka slangar. För 8 mm slang motsvarar en skarp vinkel ungefär 240 mm (30 × 8 mm) rak slang. Det innebär att 5 meter rak slang skapar cirka 21 gånger mer begränsning än en enda vinkel. System innehåller dock ofta flera olika böjar och kopplingar, vars kumulativa effekt kan överstiga förlusterna på den raka längden.
Hur påverkar snabbkopplingar systemets prestanda?
Standard snabbkopplingar ger normalt en lokal förlust som motsvarar 15-25 rördiametrar i raka rör. Ännu viktigare är att många snabbkopplingar har inre begränsningar som är mindre än deras nominella storlek. En "10 mm" snabbkoppling kan ha en intern begränsning på endast 7-8 mm, vilket skapar en borrhålsreduktion som kan minska flödeskapaciteten med 50-70% vid den punkten.
Hur påverkas systemets prestanda av delvis stängda flödesreglerventiler?
En flödesreglerventil som är stängd till 50% av sin fulla borrarea minskar inte flödet med bara 50% - den minskar flödet med cirka 75% på grund av det icke-linjära förhållandet mellan diameter och flödeskapacitet. Tryckfallet ökar med kvadraten på hastighetsförändringen, vilket innebär att en halvering av den effektiva diametern ökar tryckfallet med cirka 16 gånger under samma flödesförhållanden.
-
Ger en detaljerad genomgång av Darcy-Weisbach-ekvationen, en grundläggande och allmänt använd formel inom strömningslära för att beräkna tryckförlust på grund av friktion i ett rör. ↩
-
Ger en tydlig definition av Reynolds tal, en kritisk dimensionslös storhet som används för att förutsäga flödesmönster (laminärt eller turbulent) i olika situationer med vätskeflöden. ↩
-
Presenterar Moody-diagrammet, ett omfattande diagram som plottar Darcy-friktionsfaktorn mot Reynolds tal och relativ råhet, vilket är standardverktyget för ingenjörer för att bestämma tryckfall i rör. ↩
-
Förklarar begreppet K-värde, eller lokal förlustkoefficient, ett dimensionslöst tal som används för att karakterisera tryckförlusten i en rörkoppling eller ventil som en del av metoden för ekvivalent längd. ↩
-
Beskriver fysiken bakom det tryckfall som uppstår när en vätska passerar genom en begränsning (en öppning), baserat på principerna i kontinuitetsekvationen och Bernoullis princip. ↩



