
Kämpar du med inkonsekventa hastigheter på pneumatiska cylindrar eller oväntade effekter i slutet av slaget? Dessa vanliga problem beror ofta på en dålig förståelse för kolvkinematik. Många ingenjörer fokuserar enbart på kraftkraven och förbiser de kritiska rörelseparametrar som avgör systemets prestanda.
Kolvens kinematik1 påverkar direkt pneumatiska systems prestanda genom tryck-hastighetssamband, accelerationsgränser och dämpningskrav. Genom att förstå dessa principer kan ingenjörer dimensionera komponenterna rätt, förutse faktiska rörelseprofiler och förhindra förtida fel i stånglösa cylindrar och andra pneumatiska ställdon.
Under mina mer än 15 år på Bepto, där jag arbetat med pneumatiska system, har jag sett otaliga fall där förståelse för dessa grundläggande principer har hjälpt kunderna att lösa ihållande prestandaproblem och förlänga utrustningens livslängd med 3-5 gånger.
Innehållsförteckning
- Vilket tryck behöver du egentligen för konstant hastighet?
- Hur beräknar man den maximalt möjliga accelerationen i pneumatiska cylindrar?
- Varför är väntetiden viktig och hur beräknas den?
- Slutsats
- Vanliga frågor om kolvkinematik i pneumatiska system
Vilket tryck behöver du egentligen för konstant hastighet?
Många ingenjörer använder helt enkelt det högsta tillgängliga trycket i sina pneumatiska system, men det är ineffektivt och kan leda till ryckiga rörelser, överdrivet slitage och slöseri med energi.
Det tryck som krävs för konstant hastighet i en pneumatisk cylinder beräknas med P = (F + Fr)/A, där P är trycket, F är den externa belastningskraften, Fr är friktionsmotståndet och A är kolvytan. Denna beräkning säkerställer en jämn och effektiv drift utan överdrivet tryck som slösar energi och påskyndar komponentförslitningen.
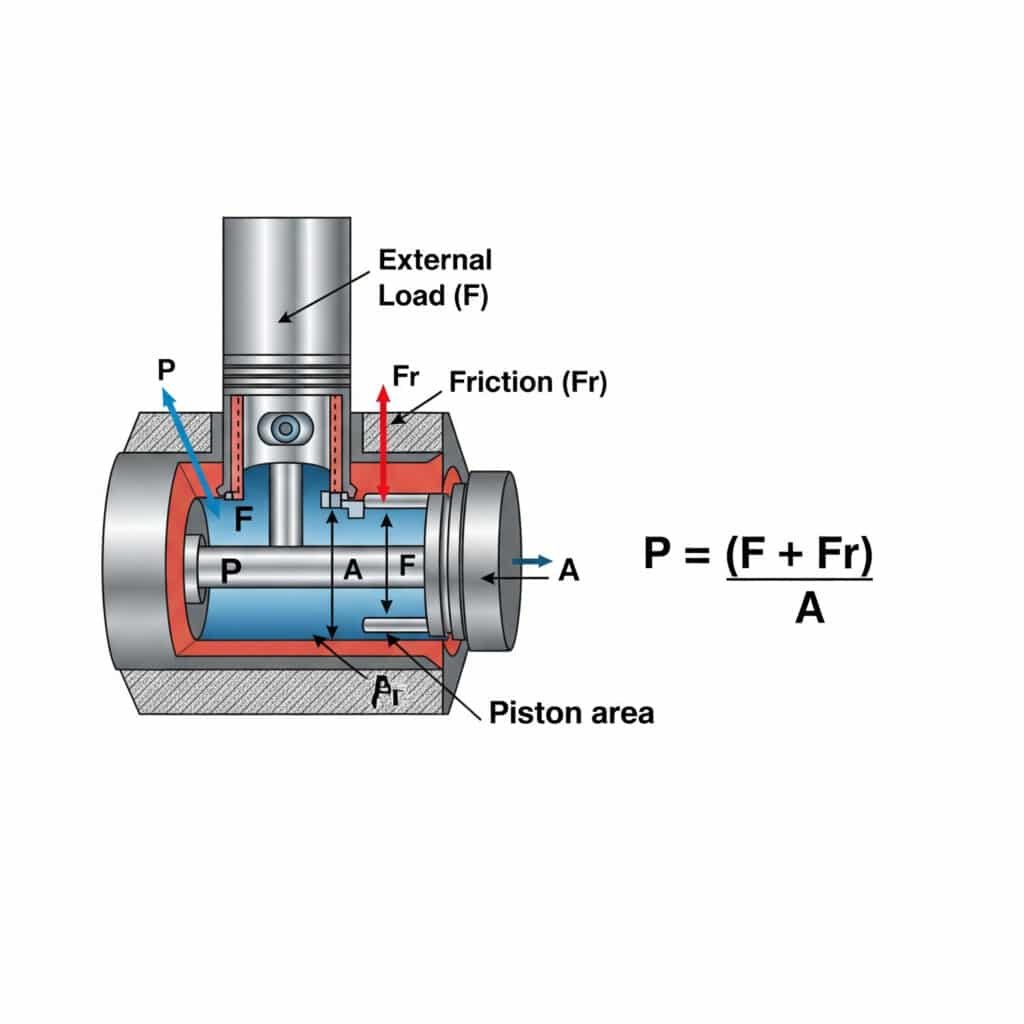
Att förstå tryckkraven för rörelse med konstant hastighet har praktiska konsekvenser för systemets utformning och drift. Låt mig bryta ner detta till praktiska insikter.
Faktorer som påverkar tryckkrav för konstant hastighet
Det tryck som krävs för att upprätthålla konstant hastighet beror på flera faktorer:
| Faktor | Påverkan på tryckkravet | Praktiska överväganden |
|---|---|---|
| Extern belastning | Direkt linjärt samband | Varierar med inriktning och externa krafter |
| Friktion | Ökar det erforderliga trycket | Förändringar med tätningsslitage och smörjning |
| Kolvområde | Omvänt proportionell | Större hål = lägre tryckbehov |
| Begränsningar i lufttillförseln | Tryckfall i ledningar/ventiler | Dimensionera komponenterna för minimalt tryckfall |
| Mottryck | Motsätter sig förslaget | Beakta avgasflödets kapacitet |
Beräkning av lägsta tryck för stabil rörelse
För att bestämma det minsta tryck som krävs för stabil rörelse:
- Beräkna den kraft som krävs för att övervinna den externa belastningen
- Lägg till friktionskraften (typiskt 3-20% av maximal kraft)
- Dividera med den effektiva kolvytan
- Lägg till en stabilitetsfaktor (typiskt 10-30%)
Till exempel i en stångfri cylinder med 40 mm hål, 10 kg last och 15% friktion:
| Parameter | Beräkning | Resultat |
|---|---|---|
| Belastning Kraft | 10kg × 9,81m/s² | 98.1N |
| Friktionskraft | 15% av maxkraft vid 6 bar | ~45N |
| Total styrka | 98,1N + 45N | 143.1N |
| Kolvområde | π × (0,02 m)². | 0.00126m² |
| Minsta tryck | 143,1 N ÷ 0,00126m² | 113.571 Pa (1,14 bar) |
| Med 20% Stabilitetsfaktor | 1,14 bar × 1,2 | 1,37 bar |
Tillämpning i den verkliga världen: Energibesparingar genom tryckoptimering
Förra året arbetade jag med Robert, en produktionsingenjör på en möbelfabrik i Michigan. Hans automatiserade monteringslinje använde stånglösa cylindrar som arbetade med ett matningstryck på hela 6 bar, oavsett belastning.
Efter att ha analyserat hans applikation konstaterade vi att de flesta rörelser endast kräver 2,5-3 bar för stabil drift. Genom att installera proportionella tryckregulatorerminskade vi luftförbrukningen med 40% samtidigt som vi behöll samma cykeltid. Detta sparade cirka $12.000 per år i energikostnader samtidigt som tätningsslitaget minskade och underhållsintervallen förlängdes.
Förhållandet mellan hastighet och tryck i verkliga system
I praktiken är förhållandet mellan tryck och hastighet inte helt linjärt på grund av:
- Flödesbegränsningar: Ventil- och portdimensionering påverkar maximalt uppnåelig hastighet
- Effekter av kompressibilitet: Luft är komprimerbar, vilket orsakar accelerationsfördröjningar
- Stick-slip-fenomen: Friktionsegenskaperna ändras med hastigheten
- Tröghetseffekter: Massacceleration kräver ytterligare kraft/tryck
Hur beräknar man den maximalt möjliga accelerationen i pneumatiska cylindrar?
Att förstå accelerationsgränserna är avgörande för att förhindra kraftiga stötar, vibrationer och förtida komponentfel i pneumatiska system.
Den maximalt möjliga accelerationen i en pneumatisk cylinder beräknas med a = (P × A - F - Fr)/m, där a är accelerationen, P är trycket, A är kolvytan, F är den externa belastningen, Fr är friktionsmotståndet och m är den rörliga massan. Denna ekvation definierar de fysiska gränserna för hur snabbt ett pneumatiskt ställdon kan starta eller stoppa en rörelse.
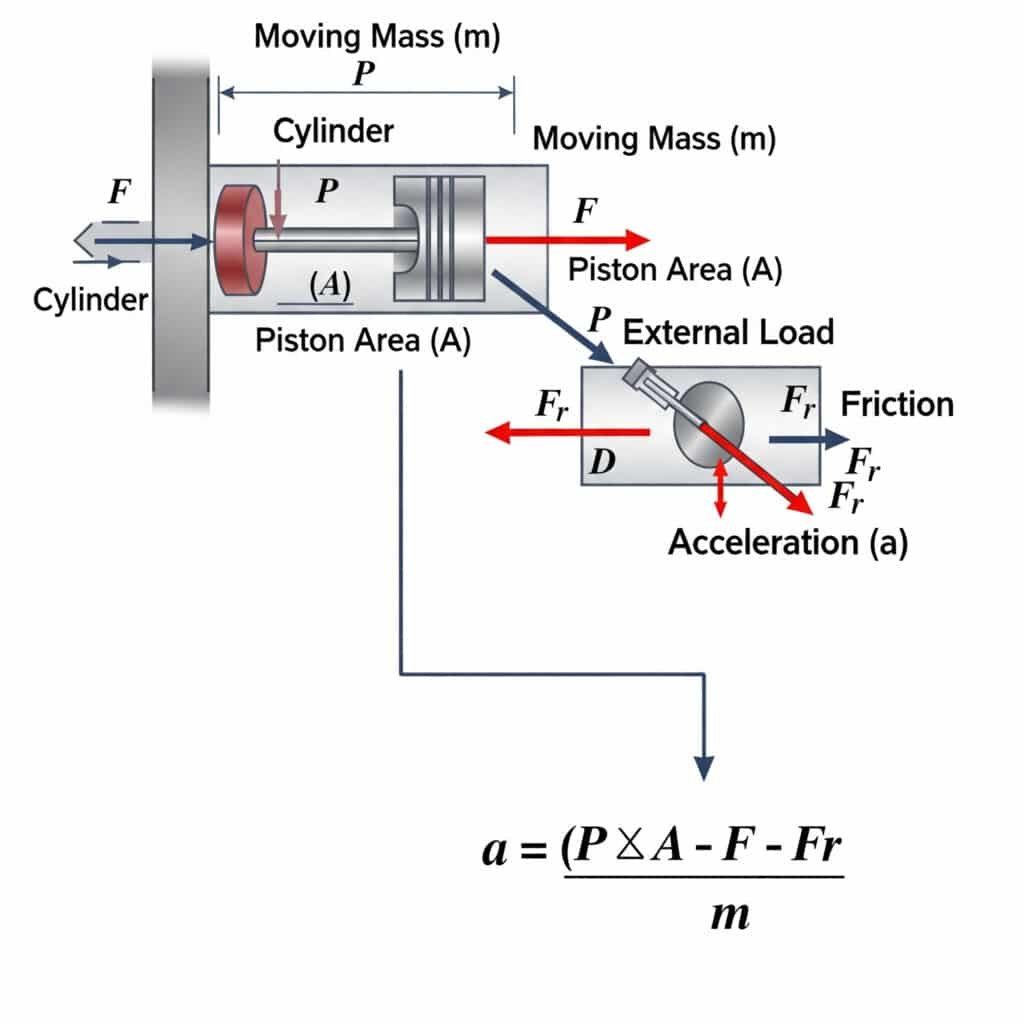
De teoretiska accelerationsgränserna har betydande praktiska konsekvenser för systemdesign och komponentval.
Härledning av accelerationens gränsekvation
Ekvationen för accelerationsgränsen kommer från Newtons andra lag2 (F = ma):
- Den nettokraft som är tillgänglig för acceleration är: Fnet = Ftryck - Flast - Ffriktion
- F-tryck = P × A
- Därför: a = Fnet/m = (P × A - F - Fr)/m
Praktiska accelerationsgränser för olika cylindertyper
Olika cylinderkonstruktioner har olika praktiska accelerationsgränser:
| Cylindertyp | Typisk Max acceleration | Begränsande faktorer |
|---|---|---|
| Standard stångcylinder | 10-15 m/s² | Stångböjning, lagerbelastningar |
| Stånglös cylinder (magnetisk) | 8-12 m/s² | Magnetisk kopplingsstyrka |
| Stånglös cylinder (mekanisk) | 15-25 m/s² | Tätning/lagerutformning, inre friktion |
| Styrcylinder | 20-30 m/s² | Styrsystemets styvhet, bärförmåga |
| Slagcylinder | 50-100+ m/s² | Speciellt utformad för hög acceleration |
Hänsyn till massa i accelerationsberäkningar
När man beräknar acceleration är det viktigt att ta med alla rörliga massor:
- Kolvmontering: Inklusive kolv, tätningar och anslutningselement
- Lastmassa: Extern last som flyttas
- Effektiv massa av rörlig luft: Ofta försumbar men relevant i höghastighetstillämpningar
- Extra massa på grund av montering av komponenter: Fästen, sensorer etc.
En gång hjälpte jag en kund i Frankrike som upplevde mystiska fel i sitt stånglösa cylindersystem. Cylindern var rätt dimensionerad för den angivna belastningen på 15 kg, men gick konsekvent sönder efter några tusen cykler.
Efter att ha undersökt saken upptäckte vi att han hade glömt att ta hänsyn till monteringsplattans och tillbehörens massa på 12 kg. Den faktiska rörliga massan var nästan dubbelt så stor som han hade beräknat, vilket orsakade accelerationskrafter som överskred cylinderns konstruktionsgränser. Efter att ha uppgraderat till en större cylinder upphörde felen helt.
Metoder för kontroll av acceleration
För att kontrollera accelerationen inom säkra gränser:
- Flödesreglerventiler: Begränsa flödeshastigheten under inledande rörelse
- Proportionella ventiler: Tillhandahåll kontrollerad tryckökning
- Acceleration i flera steg: Använd stegvisa tryckökningar
- Mekanisk dämpning: Lägg till externa stötdämpare
- Elektronisk styrning: Användning servo-pneumatiska system3 med accelerationsåterkoppling
Varför är väntetiden viktig och hur beräknas den?
Korrekt dämpning i slutet av slaget är avgörande för att förhindra slagskador, minska buller och förlänga livslängden på pneumatiska cylindrar. Förståelse för dämpningstiden hjälper ingenjörer att utforma system som balanserar cykeltid med komponenternas livslängd.
Dämpningstiden i pneumatiska cylindrar beräknas med hjälp av ekvationen t = √(2s/a), där t är tid, s är dämpningens slaglängd och a är retardation. Denna tid representerar hur lång tid det tar att på ett säkert sätt bromsa den rörliga massan före kollisionen, vilket är avgörande för att förhindra skador på cylindern och anslutna komponenter.

Låt oss utforska de praktiska aspekterna av tidsberäkningar för dämpning och vad de innebär för systemets utformning.
Fysiken bakom pneumatisk dämpning
Pneumatisk dämpning fungerar genom kontrollerad luftkompression och begränsat utblås:
- När kolven går in i kuddkammaren begränsas utblåsningsvägen
- Den instängda luften komprimeras, vilket skapar ett ökande mottryck
- Detta mottryck skapar en motkraft som bromsar kolven
- Retardationsprofilen beror på dynans utformning och justering
Beräkning av optimal tid för dämpning
Den optimala dämpningstiden balanserar stötskydd och cykeltidseffektivitet:
| Parameter | Formel | Exempel |
|---|---|---|
| Dämpningsavstånd | Baserat på cylinderkonstruktion | 15 mm (typiskt för 40 mm hål) |
| Nödvändig retardation | a = v²/(2s) | För v=0,5m/s, s=15mm: a = 8,33m/s² |
| Dämpande tid | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Tryckuppbyggnad | P = P₀(V₀/V)^γ | Beror på kuddkammarens geometri |
Faktorer som påverkar stötdämpningens prestanda
Flera faktorer påverkar den faktiska dämpningsprestandan:
- Design med dämpad tätning: Påverkar luftläckaget under dämpningen
- Justering av nålventil: Kontrollerar avgasernas begränsningsgrad
- Rörlig massa: Tyngre laster kräver längre dämpningstid
- Anflygningshastighet: Högre hastigheter kräver längre kuddavstånd
- Arbetstryck: Påverkar maximal tillgänglig motkraft
Dämpande typer och deras tillämpningar
Olika dämpningsmekanismer är lämpliga för olika användningsområden:
| Typ av dämpning | Egenskaper | Bästa applikationer |
|---|---|---|
| Fast dämpning | Enkelt, ej justerbart | Lätta belastningar, jämn drift |
| Justerbar dämpning | Avstämbar med nålventiler | Varierande belastningar, flexibla applikationer |
| Självjusterande dämpning | Anpassar sig till olika förhållanden | Ändring av hastigheter och belastningar |
| Externa stötdämpare | Hög energiabsorption | Tunga laster, höga hastigheter |
| Elektronisk dämpning | Precis kontrollerad inbromsning | Servo-pneumatiska system |
Fallstudie: Optimering av dämpning i applikationer med hög cykelbelastning
Jag arbetade nyligen med Thomas, en konstruktör på en tillverkare av bilkomponenter i Tyskland. Hans monteringslinje använde stånglösa cylindrar som arbetade med 45 cykler per minut, men hade ofta problem med tätningsfel och skador på monteringsfästena.
Analysen visade att dämpningstiden var för kort för den rörliga massan, vilket orsakade slagkrafter på nästan 3G i varje ände av slaget. Genom att öka dämpningsslaget från 12 mm till 20 mm och optimera nålventilens inställningar kunde vi förlänga dämpningstiden från 0,04 s till 0,07 s.
Denna till synes lilla förändring minskade slagkrafterna med över 60%, eliminerade konsolskadorna helt och hållet och förlängde tätningens livslängd från 3 månader till över ett år - allt detta med bibehållen cykeltid.
Praktisk procedur för justering av dämpningen
För optimal dämpningsprestanda i stånglösa cylindrar:
- Starta med dämpningsventilerna helt öppna (minimal begränsning)
- Stäng dämpningsventilen gradvis tills en jämn retardation har uppnåtts
- Test med lägsta och högsta förväntade belastning
- Verifiera dämpningsprestanda över hela hastighetsområdet
- Lyssna efter ljud från stötar som tyder på otillräcklig dämpning
- Mät faktisk retardationstid för att bekräfta beräkningarna
Slutsats
Att förstå principerna för kolvkinematik - från tryckkrav för konstant hastighet till accelerationsgränser och beräkning av dämpningstid - är avgörande för att utforma effektiva och tillförlitliga pneumatiska system. Genom att tillämpa dessa principer på dina applikationer med stånglösa cylindrar kan du optimera prestanda, minska energiförbrukningen och avsevärt förlänga komponenternas livslängd.
Vanliga frågor om kolvkinematik i pneumatiska system
Vilket tryck behöver jag för ett visst cylindervarvtal?
Det tryck som behövs beror på belastningen, friktionen och cylinderarean. Beräkna det med P = (F + Fr)/A, där F är den externa lastkraften, Fr är friktionsmotståndet och A är kolvytan. För en typisk kolvstångslös cylinder som flyttar en 10 kg tung last horisontellt behövs cirka 1,5-2 bar för stabil rörelse vid måttliga hastigheter.
Hur snabbt kan en pneumatisk cylinder accelerera?
En pneumatisk cylinders maximala acceleration beräknas med a = (P × A - F - Fr)/m. Typiska stånglösa cylindrar kan uppnå en acceleration på 10-25 m/s² beroende på konstruktion. Detta innebär att en hastighet på 0,5 m/s nås på cirka 20-50 millisekunder under optimala förhållanden.
Vilka faktorer begränsar den maximala hastigheten för en stånglös cylinder?
Den maximala hastigheten begränsas av ventilens flödeskapacitet, lufttillförselvolym, portstorlek, dämpningsförmåga och tätningsdesign. De flesta stånglösa standardcylindrar är konstruerade för maxhastigheter på 0,8-1,5 m/s, men specialiserade höghastighetscylindrar kan nå 2-3 m/s.
Hur beräknar jag rätt dämpning för min applikation?
Beräkna rätt dämpning genom att bestämma den rörliga lastens kinetiska energi (KE = ½mv²) och se till att dämpningssystemet kan absorbera denna energi. Dämpningstiden ska beräknas med t = √(2s/a), där s är dämpningsavståndet och a är den önskade retardationshastigheten.
Vad händer om min pneumatiska cylinder accelererar för snabbt?
Överdriven acceleration kan orsaka mekanisk påfrestning på monteringskomponenter, förtida slitage på tätningar, ökade vibrationer och ökat buller, potentiell lastförskjutning eller skada samt minskad precision i systemet. Det kan också leda till ryckiga rörelser som påverkar produktkvaliteten i precisionsapplikationer.
Hur påverkar lastens orientering det tryck som krävs för förflyttning?
Lastens orientering påverkar tryckkraven avsevärt. Vertikala laster som rör sig mot gravitationen kräver extra tryck för att övervinna gravitationskraften (P = F/A + Fg/A + Fr/A). Horisontella laster behöver bara övervinna friktion och tröghet. Lutande laster faller mellan dessa ytterligheter baserat på vinkelns sinus.
-
Ger en grundläggande förklaring av kinematik, den gren av mekaniken som beskriver föremåls rörelse utan att ta hänsyn till de krafter som orsakar rörelsen.
elektronisk ingångssignal, vilket möjliggör avancerad pneumatisk styrning. ↩ -
Detaljer Newtons andra lag (F=ma), den grundläggande fysikaliska principen som relaterar kraften som verkar på ett objekt till dess massa och acceleration, vilket är grunden för alla dynamiska beräkningar. ↩
-
Beskriver servopneumatik, en avancerad styrteknik som kombinerar pneumatikens kraft med precisionen hos elektronisk styrning med sluten slinga för att uppnå mycket exakta positionerings- och rörelseprofiler. ↩


