
Har du någonsin rört vid en pneumatisk cylinder efter kontinuerlig drift och blivit förvånad över hur varmt det känns? Den värmen är inte bara ett besvär - den innebär slöseri med energi, minskad effektivitet och potentiella tillförlitlighetsproblem som kan kosta din verksamhet tusentals kronor.
Värmeöverföring i pneumatiska system sker genom tre mekanismer: ledning genom komponentmaterial, konvektion mellan ytor och luft samt strålning från varma ytor. Genom att förstå och optimera dessa principer kan man sänka drifttemperaturerna med 15-30%, förlänga komponenternas livslängd med upp till 40% och förbättra energieffektiviteten med 5-15%.
Förra månaden var jag rådgivare åt en livsmedelsfabrik i Georgia där de stånglösa cylindrarna gick sönder var 3-4:e månad på grund av termiska problem. Deras underhållsteam bytte helt enkelt ut komponenter utan att ta itu med grundorsaken. Genom att tillämpa korrekta värmeöverföringsprinciper sänkte vi drifttemperaturerna med 22°C och förlängde komponenternas livslängd till över ett år. Låt mig visa dig hur vi gjorde det - och hur du kan tillämpa samma principer på dina system.
Innehållsförteckning
- Beräkning av konduktionskoefficient: Hur rör sig värme genom dina komponenter?
- Metoder för förbättrad konvektion: Vilka tekniker maximerar värmeöverföringen från luft till yta?
- Modell för strålningseffektivitet: När spelar värmestrålning roll i pneumatiska system?
- Slutsats
- Vanliga frågor om värmeöverföring i pneumatiska system
Beräkning av konduktionskoefficient: Hur rör sig värme genom dina komponenter?
Konduktion är den primära värmeöverföringsmekanismen i fasta pneumatiska komponenter. Att förstå hur man beräknar och optimerar konduktionskoefficienter är avgörande för att hantera systemtemperaturer.
Värmeledningskoefficienten kan beräknas med hjälp av Fouriers lag1: q = -k(dT/dx), där q är värmeflödet (W/m²), k är värmeledningsförmågan (W/m-K) och dT/dx är temperaturgradienten. För pneumatiska komponenter beror den effektiva ledningen på materialval, gränssnittskvalitet och geometriska faktorer som påverkar värmebanans längd och tvärsnittsarea.
Jag minns en felsökning vid en tillverkningslinje i Tennessee där de stånglösa cylinderlagren gick sönder i förtid. Underhållsteamet hade provat flera olika smörjmedel utan framgång. När vi analyserade ledningsvägarna upptäckte vi en termisk flaskhals vid gränssnittet mellan lager och hölje. Genom att förbättra ytfinishen och applicera en termiskt ledande förening ökade vi den effektiva ledningskoefficienten med 340% och eliminerade felen helt.
Grundläggande ledningsekvationer
Låt oss bryta ner de viktigaste ekvationerna för att beräkna ledning i pneumatiska komponenter:
Fouriers lag för värmeledning
Den grundläggande ekvationen som styr värmeledning är:
q = -k(dT/dx)
Var?
- q = värmeflöde (W/m²)
- k = värmeledningsförmåga (W/m-K)
- dT/dx = Temperaturgradient (K/m)
För ett enkelt endimensionellt fall med konstant tvärsnitt:
Q = kA(T₁-T₂)/L
Var?
- Q = Värmeöverföringshastighet (W)
- A = Tvärsnittsarea (m²)
- T₁, T₂ = Temperaturer i varje ände (K)
- L = längd på värmebana (m)
Begreppet värmemotstånd
För komplexa geometrier är metoden med värmemotstånd ofta mer praktisk:
R = L/(kA)
Var?
- R = Termiskt motstånd (K/W)
För system med flera komponenter i serie:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
Och värmeöverföringshastigheten blir:
Q = ΔT/Rtotal
Jämförelse av materialens värmeledningsförmåga
| Material | Termisk konduktivitet (W/m-K) | Relativ konduktivitet | Vanliga tillämpningar |
|---|---|---|---|
| Aluminium | 205-250 | Hög | Cylindrar, kylflänsar |
| Stål | 36-54 | Medium | Strukturella komponenter |
| Rostfritt stål | 14-16 | Låg-Medium | Korrosiva miljöer |
| Brons | 26-50 | Medium | Lager, bussningar |
| PTFE | 0.25 | Mycket låg | Tätningar, lager |
| Nitrilgummi | 0.13 | Mycket låg | O-ringar, tätningar |
| Luft (stillastående) | 0.026 | Extremt låg | Fyller igen luckor |
| Termisk pasta | 3-8 | Låg | Material för gränssnitt |
Kontaktmotstånd i pneumatiska aggregat
Vid gränssnitt mellan komponenter påverkar kontaktmotståndet värmeöverföringen avsevärt:
Rkontakt = 1/(hc × A)
Var?
- hc = Kontaktkoefficient (W/m²-K)
- A = Kontaktyta (m²)
Faktorer som påverkar kontaktmotståndet är bl.a:
- Ytjämnhet: Ojämnare ytor har mindre faktisk kontaktyta
- Kontakt Tryck: Högre tryck ökar den effektiva kontaktytan
- Gränssnittsmaterial: Termiska föreningar fyller luftspalter
- Ytans renhet: Föroreningar kan öka motståndskraften
Fallstudie: Termisk optimering av stånglösa cylindrar
För en magnetisk stångfri cylinder som har termiska problem:
| Komponent | Ursprunglig design | Optimerad design | Förbättring |
|---|---|---|---|
| Cylinderhus | Anodiserad aluminium | Samma material, förbättrad finish | 15% bättre ledning |
| Lagergränssnitt | Metall-mot-metall-kontakt | Tillsatt termisk förening | 340% bättre ledningsförmåga |
| Monteringsfästen | Målat stål | Blank aluminium | 280% bättre ledningsförmåga |
| Övergripande termisk resistans | 2,8 K/W | 0,7 K/W | 75% reducering |
| Driftstemperatur | 78°C | 56°C | 22°C sänkning |
| Komponentens livslängd | 4 månader | >12 månader | 3× förbättring |
Praktiska tekniker för ledningsoptimering
Baserat på min erfarenhet av hundratals pneumatiska system följer här de mest effektiva metoderna för att förbättra ledningsförmågan:
Optimering av gränssnitt
- Ytbehandling: Förbättra kontaktytans jämnhet till Ra 0,4-0,8 μm
- Material för termiska gränssnitt2: Applicera lämpliga föreningar (3-8 W/m-K)
- Fästelementets vridmoment: Säkerställ korrekt åtdragning för optimalt kontakttryck
- Renlighet: Avlägsna alla oljor och föroreningar före montering
Strategier för materialval
- Kritiska värmebanor: Använd material med hög ledningsförmåga (aluminium, koppar)
- Termiska pauser: Avsiktlig användning av material med låg ledningsförmåga för att isolera värme
- Sammansatta tillvägagångssätt: Kombinera material för optimal prestanda/kostnad
- Anisotropa material: Använd riktad konduktivitet där så är lämpligt
Geometrisk optimering
- Längd på värmebana: Minimera avståndet mellan värmekällor och kylflänsar
- Tvärsnittsarea: Maximera ytan vinkelrätt mot värmeflödet
- Termiska flaskhalsar: Identifiera och eliminera förträngningar i värmevägen
- Redundanta banor: Skapa flera parallella ledningsvägar
Metoder för förbättrad konvektion: Vilka tekniker maximerar värmeöverföringen från luft till yta?
Konvektion är ofta den begränsande faktorn vid kylning av pneumatiska system. Genom att förbättra den konvektiva värmeöverföringen kan man dramatiskt förbättra värmehanteringen och systemets prestanda.
Konvektiv värmeöverföring följer Newtons lag för kylning3: Q = hA(Ts-T∞), där h är konvektionskoefficienten (W/m²-K), A är ytarean och (Ts-T∞) är temperaturskillnaden mellan ytan och vätskan. Förbättringsmetoderna inkluderar att öka ytarean genom fenor, förbättra vätskehastigheten med riktat luftflöde och optimera ytegenskaperna för att främja turbulenta gränsskikt.
Under en energieffektivitetsrevision på en förpackningsanläggning i Arizona stötte jag på ett pneumatiskt system som arbetade i en omgivande miljö på 43 °C. De stavlösa cylindrarna överhettades trots att de uppfyllde alla underhållskrav. Genom att implementera riktad konvektionsförbättring - lägga till små aluminiumfenor och en lågeffektsfläkt - ökade vi konvektionskoefficienten med 450%. Detta sänkte drifttemperaturerna från farliga nivåer till inom specifikationerna utan några större systemändringar.
Grundläggande konvektionsvärmeöverföring
Den grundläggande ekvationen som styr konvektiv värmeöverföring är:
Q = hA(Ts-T∞)
Var?
- Q = Värmeöverföringshastighet (W)
- h = konvektionskoefficient (W/m²-K)
- A = Ytarea (m²)
- Ts = yttemperatur (K)
- T∞ = vätskans (luftens) temperatur (K)
Konvektionskoefficienten h beror på flera faktorer:
- Vätskeegenskaper (densitet, viskositet, värmeledningsförmåga)
- Flödesegenskaper (hastighet, turbulens)
- Ytgeometri och orientering
- Flödesregim (naturlig kontra forcerad konvektion)
Naturlig kontra forcerad konvektion
| Parameter | Naturlig konvektion | Forcerad konvektion | Konsekvenser |
|---|---|---|---|
| Typiskt h-värde | 5-25 W/m²-K | 25-250 W/m²-K | Forcerad konvektion kan vara 10× mer effektiv |
| Drivande kraft | Flytkraft (temperaturskillnad) | Externt tryck (fläktar, blåsmaskiner) | Forcerad konvektion är mindre temperaturberoende |
| Flödesmönster | Vertikalt flöde längs ytor | Riktad baserat på forceringsmekanism | Det forcerade flödet kan optimeras för specifika komponenter |
| Tillförlitlighet | Passiv, alltid närvarande | Kräver kraft och underhåll | Naturlig konvektion ger kylning i baslinjen |
| Utrymmesbehov | Kräver utrymme för luftcirkulation | Kräver utrymme för luftkonditioneringsaggregat och kanaler | Tvångsstyrda system behöver mer planering |
Tekniker för förbättrad konvektion
Förstärkning av ytarea
Ökad effektiv yta genom:
Fenor och förlängda ytor
- Stiftformade fenor: Omnidirektionellt luftflöde, 150-300% ytökning
- Lameller av plåt: Riktat luftflöde, 200-500% ytökning
- Korrugerade ytor: Måttlig förbättring, 50-150% områdesökningGrovbearbetning av ytor
- Mikrotexturering: 5-15% effektiv ytökning
- Dimmiga ytor: 10-30%-ökning plus gränsskiktseffekter
- Räfflade mönster: 15-40% ökar med riktningsfördelar
Flödesmanipulering
Förbättrade luftflödesegenskaper genom:
System för forcerad luft
- Fläktar: Riktat luftflöde, 200-600% h förbättring
- Blåsmaskiner: Högtrycksflöde, 300-800% h förbättring
- Jetstrålar med komprimerad luft: Riktad kylning, 400-1000% lokal h förbättringOptimering av flödesvägar
- Bafflar: Rikta luften till kritiska komponenter
- Venturi-effekter: Accelererar luft över specifika ytor
- Virvelgeneratorer: Skapa turbulens för störning av gränsskiktet
Modifieringar av ytan
Förändring av ytegenskaper för att förbättra konvektionen:
Emissivitetsbehandlingar
- Svart oxid: Ökar emissiviteten till 0,7-0,9
- Anodisering: Kontrollerad emissivitet från 0,4-0,9
- Färger och ytbeläggningar: Anpassningsbar emissivitet upp till 0,98Kontroll av vätbarhet
- Hydrofila beläggningar: Förbättrar vätskekylning
- Hydrofoba ytor: Förhindrar problem med kondens
- Mönstrad vätbarhet: Riktat kondensatflöde
Exempel på praktisk implementering
För en stånglös pneumatisk cylinder som arbetar i en miljö med höga temperaturer:
| Förbättringsmetod | Implementering | h Förbättring | Sänkning av temperaturen |
|---|---|---|---|
| Stiftflänsar (6 mm) | Fästbara fenor av aluminium, 10 mm mellanrum | 180% | 12°C |
| Riktat luftflöde | 80 mm, 2 W DC-fläkt vid 1,5 m/s | 320% | 18°C |
| Ytbehandling | Svart anodisering | 40% | 3°C |
| Kombinerat tillvägagångssätt | Alla metoder integrerade | 450% | 24°C |
Nusseltalskorrelation för konstruktionsberäkningar
För tekniska beräkningar ska Nusseltal4 (Nu) ger en dimensionslös metod för konvektion:
Nu = hL/k
Var?
- L = Karakteristisk längd
- k = vätskans värmeledningsförmåga
För forcerad konvektion över en plan platta:
Nu = 0,664Re^(1/2)Pr^(1/3) (laminärt flöde)
Nu = 0,037Re^(4/5)Pr^(1/3) (turbulent flöde)
Var?
- Re = Reynolds tal (hastighet × längd × densitet / viskositet)
- Pr = Prandtl-tal (specifik värme × viskositet / värmeledningsförmåga)
Dessa korrelationer gör det möjligt för ingenjörer att förutsäga konvektionskoefficienter för olika konfigurationer och optimera kylstrategier därefter.
Modell för strålningseffektivitet: När spelar värmestrålning roll i pneumatiska system?
Strålning förbises ofta vid termisk hantering av pneumatiska system, men den kan stå för 15-30% av den totala värmeöverföringen i många applikationer. Att förstå när och hur man optimerar den radiativa värmeöverföringen är avgörande för en heltäckande värmehantering.
Värmeöverföring genom strålning följer Stefan-Boltzmanns lag5: Q = εσA(T₁⁴-T₂⁴), där ε är ytans emissivitet, σ är Stefan-Boltzmann-konstanten, A är ytan och T₁ och T₂ är de absoluta temperaturerna för den emitterande ytan och omgivningen. Strålningseffektiviteten i pneumatiska system beror i första hand på ytans emissivitet, temperaturskillnad och visningsfaktorer mellan komponenter och deras omgivning.
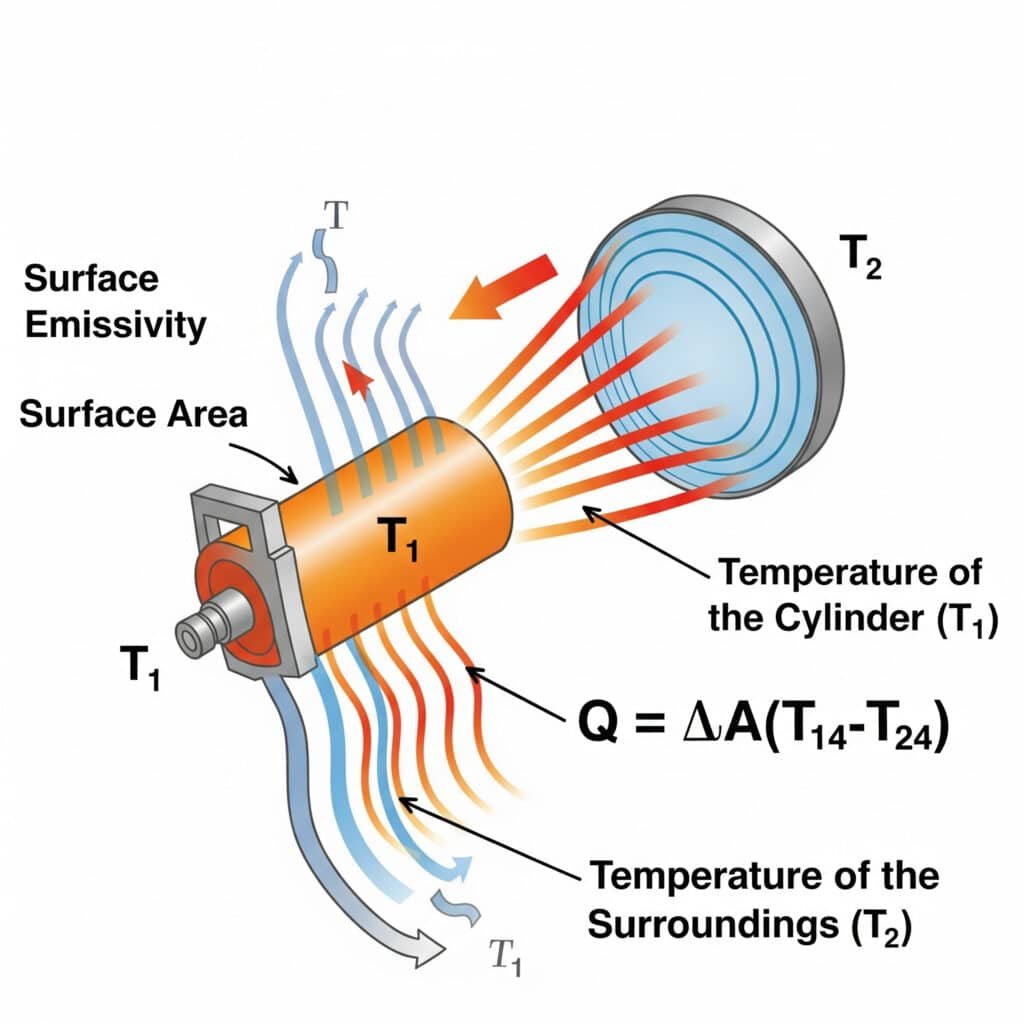
Jag hjälpte nyligen en tillverkare av halvledarutrustning i Oregon att lösa problem med överhettning i deras stånglösa precisionscylindrar. Deras ingenjörer hade fokuserat uteslutande på ledning och konvektion men förbisett strålning. Genom att applicera en beläggning med hög emissivitet (öka ε från 0,11 till 0,92) förbättrade vi den radiativa värmeöverföringen med över 700%. Denna enkla, passiva lösning sänkte drifttemperaturen med 9°C utan några rörliga delar eller energiförbrukning - ett kritiskt krav i deras renrumsmiljö.
Grundläggande om värmeöverföring genom strålning
Den grundläggande ekvationen som styr radiativ värmeöverföring är:
Q = εσA(T₁⁴-T₂⁴)
Var?
- Q = Värmeöverföringshastighet (W)
- ε = Emissivitet (dimensionslös, 0-1)
- σ = Stefan-Boltzmanns konstant (5,67 × 10-⁸ W/m²-K⁴)
- A = Ytarea (m²)
- T₁ = Ytans absoluta temperatur (K)
- T₂ = Omgivningens absoluta temperatur (K)
Värden för ytemissivitet för vanliga pneumatiska material
| Material/yta | Emissivitet (ε) | Strålningseffektivitet | Förbättringspotential |
|---|---|---|---|
| Polerad aluminium | 0.04-0.06 | Mycket dålig | >1500% förbättring möjlig |
| Anodiserad aluminium | 0.7-0.9 | Utmärkt | Redan optimerad |
| Rostfritt stål (polerat) | 0.07-0.14 | Dålig | >600% förbättring möjlig |
| Rostfritt stål (oxiderat) | 0.6-0.85 | Bra | Måttlig förbättring möjlig |
| Stål (polerat) | 0.07-0.10 | Dålig | >900% förbättring möjlig |
| Stål (oxiderat) | 0.7-0.9 | Utmärkt | Redan optimerad |
| Målade ytor | 0.8-0.98 | Utmärkt | Redan optimerad |
| PTFE (vit) | 0.8-0.9 | Utmärkt | Redan optimerad |
| Nitrilgummi | 0.86-0.94 | Utmärkt | Redan optimerad |
Överväganden om visningsfaktor
Strålningsutbytet beror inte bara på emissiviteten utan också på de geometriska förhållandena mellan ytorna:
F₁₂ = Andel av den strålning som lämnar yta 1 som träffar yta 2
För komplexa geometrier kan vyfaktorer beräknas med hjälp av:
- Analytiska lösningar för enkla geometrier
- Visa faktor algebra för att kombinera kända lösningar
- Numeriska metoder för komplexa arrangemang
- Empiriska approximationer för praktisk ingenjörskonst
Strålningens temperaturberoende
Temperaturförhållandet med den fjärde kraften gör att strålningen är särskilt effektiv vid högre temperaturer:
| Yttemperatur | Procentuell andel av värmeöverföringen genom strålning*. |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Förutsätter naturliga konvektionsförhållanden, ε = 0,8, 25°C omgivande temperatur
Strategier för förbättrad strålningseffektivitet
Baserat på min erfarenhet av industriella pneumatiska system är här de mest effektiva metoderna för att förbättra strålningsvärmeöverföringen:
Modifiering av ytemissivitet
Beläggningar med hög emissivitet
- Svart anodisering för aluminium (ε ≈ 0,8-0,9)
- Svartoxid för stål (ε ≈ 0,7-0,8)
- Keramiska specialbeläggningar (ε ≈ 0,9-0,98)Texturering av ytor
- Mikroruggning ökar den effektiva emissiviteten
- Porösa ytor förbättrar strålningsegenskaperna
- Kombinerad emissivitet/konvektionsförbättring
Miljöoptimering
Omgivningens temperaturreglering
- Avskärmning från het utrustning/processer
- Svala väggar/tak för bättre strålningsutbyte
- Reflekterande barriärer för att rikta strålningen mot svalare ytorVisa faktorförbättring
- Orientering för att maximera exponeringen för svala ytor
- Avlägsnande av blockerande föremål
- Reflektorer för att förbättra strålningsutbytet med svalare områden
Fallstudie: Strålningsförbättring i precisionspneumatik
För en stånglös cylinder med hög precision i en renrumsmiljö:
| Parameter | Ursprunglig design | Strålningsförstärkt design | Förbättring |
|---|---|---|---|
| Ytmaterial | Polerad aluminium (ε ≈ 0,06) | Keramiskt belagd aluminium (ε ≈ 0,94) | 1467% ökning av emissivitet |
| Värmeöverföring genom strålning | 2.1W | 32.7W | 1457% ökning av strålning |
| Driftstemperatur | 68°C | 59°C | 9°C sänkning |
| Komponentens livslängd | 8 månader | >24 månader | 3× förbättring |
| Kostnad för implementering | – | $175 per cylinder | 4,2 månaders återbetalning |
Strålning jämfört med andra värmeöverföringsmetoder
Att förstå när strålningen dominerar är avgörande för effektiv värmehantering:
| Skick | Dominans i ledningsnätet | Konvektionens dominans | Strålningsdominans |
|---|---|---|---|
| Temperaturområde | Låg till hög | Låg till medelhög | Medelhög till hög |
| Materialegenskaper | Material med hög k | Låg k, hög ytarea | Höga ε-ytor |
| Miljöfaktorer | God termisk kontakt | Luft i rörelse, fläktar | Stor temperaturskillnad |
| Utrymmesbegränsningar | Tät förpackning | Öppet luftflöde | Utsikt mot svalare omgivningar |
| Bästa applikationer | Komponenternas gränssnitt | Allmän kylning | Varma ytor, vakuum, stillastående luft |
Slutsats
Att behärska principerna för värmeöverföring - beräkning av ledningskoefficient, metoder för konvektionsförbättring och modellering av strålningseffektivitet - utgör grunden för effektiv värmehantering i pneumatiska system. Genom att tillämpa dessa principer kan du sänka drifttemperaturerna, förlänga komponenternas livslängd och förbättra energieffektiviteten samtidigt som du säkerställer tillförlitlig drift även i utmanande miljöer.
Vanliga frågor om värmeöverföring i pneumatiska system
Vilken är den typiska temperaturökningen i pneumatiska cylindrar under drift?
Pneumatiska cylindrar utsätts normalt för temperaturhöjningar på 20-40°C över omgivande temperatur under kontinuerlig drift. Denna ökning beror på friktion mellan tätningar och cylinderväggar, kompressionsuppvärmning av luft och mekaniskt arbete som omvandlas till värme. Stånglösa cylindrar upplever ofta högre temperaturhöjningar (30-50°C) på grund av deras mer komplexa tätningssystem och koncentrerad värmeutveckling i lager/tätningsenheten.
Hur påverkar arbetstrycket värmeutvecklingen i pneumatiska system?
Drifttrycket har en betydande inverkan på värmeutvecklingen, där högre tryck skapar mer värme genom flera olika mekanismer. Varje ökning av drifttrycket med 1 bar ökar normalt värmeutvecklingen med 8-12% på grund av större friktionskrafter mellan tätningar och ytor, högre kompressionsvärme och ökade läckagerelaterade förluster. Detta förhållande är ungefär linjärt inom normala driftområden (3-10 bar).
Vilken är den optimala kylningsmetoden för pneumatiska komponenter i olika miljöer?
Den optimala kylningsmetoden varierar beroende på miljön: i rena miljöer med måttlig temperatur (15-30°C) räcker det ofta med naturlig konvektion och rätt avstånd mellan komponenterna. I miljöer med höga temperaturer (30-50°C) krävs forcerad konvektion med hjälp av fläktar eller tryckluft. I extremt varma miljöer (>50°C) eller där luftflödet är begränsat kan aktiva kylmetoder som termoelektriska kylare eller vätskekylning krävas. I samtliga fall ger maximering av strålningen genom ytor med hög emissivitet ytterligare passiv kylning.
Hur beräknar jag den totala värmeöverföringen från en pneumatisk komponent?
Beräkna den totala värmeöverföringen genom att summera bidragen från varje mekanism: Qtotal = Qledning + Qkonvektion + Qstrålning. För ledning, använd Q = kA(T₁-T₂)/L för varje värmeväg. För konvektion används Q = hA(Ts-T∞) med lämpliga konvektionskoefficienter. För strålning används Q = εσA(T₁⁴-T₂⁴). I de flesta industriella pneumatiska applikationer som arbetar vid 30-80°C är den ungefärliga fördelningen 20-40% ledning, 40-70% konvektion och 10-30% strålning.
Vilket är sambandet mellan temperatur och livslängd för pneumatiska komponenter?
Komponenternas livslängd minskar exponentiellt med ökande temperatur, enligt ett modifierat Arrhenius-samband. En tumregel är att varje ökning av driftstemperaturen med 10°C minskar livslängden för tätningar och komponenter med 40-50%. Det innebär att en komponent som arbetar vid 70°C kanske bara håller en tredjedel så länge som samma komponent vid 50°C. Detta förhållande är särskilt kritiskt för polymerkomponenter som tätningar, lager och packningar, som ofta bestämmer underhållsintervallet för pneumatiska system.
-
Ger en grundläggande förklaring av Fouriers lag, den grundläggande princip som beskriver hur värme leds genom fasta material baserat på deras värmeledningsförmåga och temperaturgradient. ↩
-
Förklarar funktion och typer av TIM-material (Thermal Interface Materials), som används för att fylla mikroskopiska luftspalter mellan komponenter för att förbättra värmeledningen och minska värmemotståndet. ↩
-
Beskriver principerna för Newtons lag om kylning, som styr hur föremål kyls genom att överföra värme till den omgivande vätskan via konvektion, en nyckelfaktor i utformningen av systemkylning. ↩
-
Ger en djupgående inblick i Nusselt-talet, en kritisk dimensionslös storhet inom fluiddynamik och värmeöverföring som representerar förhållandet mellan konvektiv och konduktiv värmeöverföring över en gräns. ↩
-
Beskriver Stefan-Boltzmanns lag, den grundläggande fysikaliska princip som kvantifierar den totala energi som utstrålas av en svart kropp, vilket är nödvändigt för att beräkna värmeförlust från varma ytor. ↩


