Ingenjörer räknar ofta fel på stångytorna när de konstruerar pneumatiska cylindersystem, vilket leder till felaktiga kraftberäkningar och systemfel.
Stavens area är den cirkulära tvärsnittsarean beräknad som A = πr² eller A = π(d/2)², där "r" är stavens radie och "d" är stavens diameter, vilket är avgörande för kraft- och tryckberäkningar.
Igår hjälpte jag Carlos, en konstruktör från Mexiko, vars pneumatiska system inte fungerade eftersom han glömt att subtrahera stångens area från kolvens area i sina kraftberäkningar för dubbelverkande cylindrar.
Innehållsförteckning
- Vad är stångarea i pneumatiska cylindersystem?
- Hur beräknar man stavens tvärsnittsarea?
- Varför är stavens area viktig för kraftberäkningar?
- Hur påverkar vevstakens area cylinderns prestanda?
Vad är stångarea i pneumatiska cylindersystem?
Kolvstångens area representerar kolvstångens cirkulära tvärsnittsarea, vilket är viktigt för att beräkna effektiva kolvytor och kraftuttag i dubbelverkande pneumatiska cylindrar.
Stångarea är den cirkulära area som upptas av kolvstångens tvärsnitt, mätt vinkelrätt mot stångaxeln, och som används för att bestämma effektiva nettoytor för kraftberäkningar.
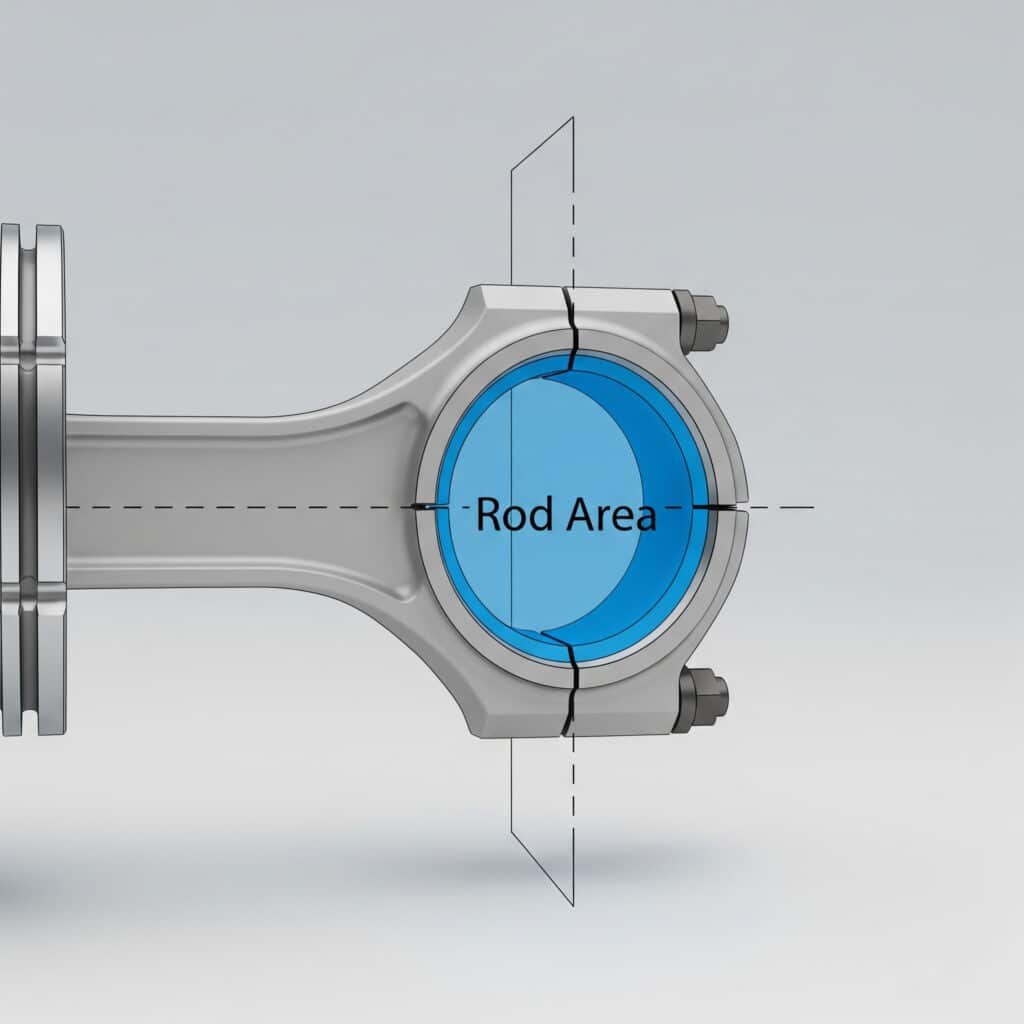
Definition av stavområde
Geometriska egenskaper
- Cirkulärt tvärsnitt: Standard stånggeometri
- Vinkelrät mätning: 90° till stångens centrumlinje
- Konstant yta: Enhetlig längs stångens längd
- Fast område: Tvärsnitt av komplett material
Viktiga mätningar
- Stångdiameter: Primär dimension för beräkning av yta
- Stångens radie: Mätning av halva diametern
- Tvärsnittsarea: Ansökan om formel för cirkulär yta
- Effektivt område: Påverkan på cylinderns prestanda
Förhållandet mellan kolvstångens och kolvens area
| Komponent | Formel för area | Syfte | Tillämpning |
|---|---|---|---|
| Kolv | A = π(D/2)² | Fullt borrningsområde | Utöka kraftberäkningen |
| Stång | A = π(d/2)² | Tvärsnitt av stång | Beräkning av indragningskraft |
| Nettoarea | A_kolv - A_stav | Effektivt indragningsområde | Dubbelverkande cylindrar |
| Ringformad yta1 | π(D² - d²)/4 | Ringformad yta | Tryck på stångsidan |
Standardstångstorlekar
Vanliga stångdiametrar
- 8mm stång: Area = 50,3 mm²
- 12 mm stång: Area = 113,1 mm²
- 16 mm stång: Area = 201,1 mm²
- 20 mm stång: Area = 314,2 mm²
- 25 mm stång: Area = 490,9 mm²
- 32 mm stång: Area = 804,2 mm²
Förhållande mellan stång och borrhål
- Standardförhållande: Stångdiameter = 0,5 × borrhålsdiameter
- Kraftig konstruktion: Stångdiameter = 0,6 × borrhålsdiameter
- Lätta arbetsuppgifter: Stångdiameter = 0,4 × borrhålsdiameter
- Anpassade applikationer: Varierar beroende på krav
Applikationer för stavområdet
Kraftberäkningar
Jag använder stavområdet för:
- Förläng kraften: Full kolvarea × tryck
- Indragningskraft: (Kolvarea - Stångarea) × tryck
- Kraftskillnad: Skillnaden mellan extend/retract
- Belastningsanalys: Anpassa cylindern till applikationen
Systemdesign
Rod område påverkar:
- Val av cylinder: Rätt dimensionering för olika applikationer
- Beräkningar av hastighet: Flödeskrav för varje riktning
- Krav på tryck: Specifikationer för systemtryck
- Optimering av prestanda: Balanserad driftdesign
Stångarea i olika cylindertyper
Enkelverkande cylindrar
- Ingen påverkan på stavområdet: Fjäderreturfunktion
- Endast utdragbar kraft: Fullt kolvområde effektivt
- Förenklade beräkningar: Ingen hänsyn till indragningskraft
- Kostnadsoptimering: Minskad komplexitet
Dubbelverkande cylindrar
- Stångens yta kritisk: Påverkar indragningskraften
- Asymmetrisk drift: Olika krafter i varje riktning
- Komplexa beräkningar: Måste överväga båda områdena
- Balansering av prestanda: Designöverväganden krävs
Stånglösa cylindrar
- Ingen stångyta: Elimineras från konstruktionen
- Symmetrisk drift: Lika stora krafter i båda riktningarna
- Förenklade beräkningar: Hänsyn till enstaka områden
- Fördelar med utrymme: Inga krav på förlängning av stången
Hur beräknar man stavens tvärsnittsarea?
Beräkning av stångens tvärsnittsarea använder standardformeln för cirkulär area med mätningar av stångens diameter eller radie för korrekt design av pneumatiska system.
Beräkna stavens area med A = πr² (med radie) eller A = π(d/2)² (med diameter), där π = 3,14159, och se till att enheterna är konsekventa genom hela beräkningen.
Grundläggande formel för area
Använda stavradie
A = πr²
- A: Tvärsnittsarea för stången
- π: 3,14159 (matematisk konstant)
- r: Stångens radie (diameter ÷ 2)
- Enheter: Area i radienheter i kvadrat
Använda stångdiameter
A = π(d/2)² eller A = πd²/4
- A: Tvärsnittsarea för stången
- π: 3.14159
- d: Stångdiameter
- Enheter: Area i diameterenheter i kvadrat
Steg-för-steg-beräkning
Mätningsprocess
- Mät stångens diameter: Använd skjutmått för noggrannhet
- Verifiera mätningen: Gör flera avläsningar
- Beräkna radie: r = diameter ÷ 2 (om radieformeln används)
- Applicera formel: A = πr² eller A = π(d/2)²
- Kontrollera enheter: Säkerställa ett enhetligt system
Exempel på beräkning
För en stång med 20 mm diameter:
- Metod 1: A = π(10)² = π × 100 = 314,16 mm²
- Metod 2: A = π(20)²/4 = π × 400/4 = 314,16 mm²
- Verifiering: Båda metoderna ger identiska resultat
Tabell för beräkning av stavarea
| Stångdiameter | Stavens radie | Beräkning av yta | Stångområde |
|---|---|---|---|
| 8 mm | 4 mm | π × 4² | 50,3 mm² |
| 12 mm | 6 mm | π × 6² | 113,1 mm² |
| 16 mm | 8 mm | π × 8² | 201,1 mm² |
| 20 mm | 10 mm | π × 10² | 314,2 mm² |
| 25 mm | 12,5 mm | π × 12.5² | 490,9 mm² |
| 32 mm | 16 mm | π × 16² | 804,2 mm² |
Verktyg för mätning
Digitala skjutmått
- Noggrannhet: ±0,02 mm precision
- Räckvidd: 0-150 mm typiskt
- Funktioner: Digital display, enhetsomvandling
- Bästa praxis: Flera mätpunkter
Mikrometer
- Noggrannhet: ±0,001 mm precision
- Räckvidd: Olika storlekar tillgängliga
- Funktioner: Spärrstopp, digitala alternativ
- Tillämpningar: Krav på hög precision
Vanliga beräkningsfel
Misstag vid mätning
- Diameter vs radie: Använda fel dimension i formel
- Inkonsekvens i enheten: Blandning av mm och tum
- Precisionsfel: Otillräckligt antal decimaler
- Kalibrering av verktyg: Okalibrerade mätinstrument
Fel i formeln
- Felaktig formel: Använda omkrets istället för area
- Saknas π: Glömska av matematisk konstant
- Kvadratfel: Felaktig tillämpning av exponent
- Omräkning av enheter: Felaktiga enhetsomvandlingar
Verifieringsmetoder
Tekniker för dubbelkontroll
- Flera beräkningar: Olika formelmetoder
- Verifiering av mätning: Upprepa diametermätningarna
- Referenstabeller: Jämför med standardvärden
- CAD-programvara: Beräkningar av 3D-modellens yta
Kontroll av skälighet
- Korrelation mellan storlek: Större diameter = större yta
- Standardjämförelser: Matcha typiska stavstorlekar
- Lämplighet för tillämpning: Lämplig för cylinderstorlek
- Tillverkningsstandarder: Vanliga tillgängliga storlekar
Avancerade beräkningar
Ihåliga stänger
A = π(D² - d²)/4
- D: Yttre diameter
- d: Innerdiameter
- Tillämpning: Viktminskning, intern routing
- Beräkning: Subtrahera inre område från yttre område
Icke-cirkulära stavar
- Fyrkantiga stavar: A = sida²
- Rektangulära stavar: A = längd × bredd
- Speciella former: Använda lämpliga geometriska formler
- Tillämpningar: Förhindra rotation, särskilda krav
När jag arbetade med Jennifer, en pneumatisk systemkonstruktör från Kanada, beräknade hon först stavarean felaktigt genom att använda diameter istället för radie i πr²-formeln, vilket resulterade i en 4× överskattning och helt felaktiga kraftberäkningar för hennes dubbelverkande cylinderapplikation.
Varför är stavens area viktig för kraftberäkningar?
Stångarean påverkar direkt den effektiva kolvarean på stångsidan av dubbelverkande cylindrar, vilket skapar kraftskillnader mellan ut- och indragningsoperationer.
Stångarean minskar den effektiva kolvarean vid indragning, vilket skapar lägre indragningskraft jämfört med utdragningskraft i dubbelverkande cylindrar, vilket kräver kompensation i systemkonstruktionen.
Grundläggande kraftberäkning
Grundläggande kraftformel
- Förläng kraften: F = P × A_kolv
- Indragningskraft: F = P × (A_kolv - A_stång)
- Skillnad i kraft: Utöka kraften > Dra tillbaka kraften
- Designpåverkan: Måste beakta båda riktningarna
Effektiva områden
- Fullt kolvområde: Tillgänglig under förlängning
- Netto kolvarea: Kolvområde minus stångområde under indragning
- Ringformad yta: Ringformat område på stångsidan
- Förhållande mellan ytor: Fastställer kraftdifferentialen
Exempel på kraftberäkning
63 mm borrhål, 20 mm vevstake Cylinder
- Kolvarea: π(31,5)² = 3.117 mm²
- Stångens yta: π(10)² = 314 mm²
- Nettoarea: 3.117 - 314 = 2.803 mm²
- Vid 6 bars tryck:
– Förläng kraften: 6 × 3,117 = 18,702 N
– Indragningskraft: 6 × 2,803 = 16,818 N
– Skillnad i kraft: 1.884 N (10%-reduktion)
Jämförelsetabell för styrkor
| Cylinderstorlek | Kolvområde | Stångområde | Nettoarea | Kraftförhållande |
|---|---|---|---|---|
| 32 mm/12 mm | 804 mm² | 113 mm² | 691 mm² | 86% |
| 50 mm/16 mm | 1 963 mm² | 201 mm² | 1.762 mm² | 90% |
| 63 mm/20 mm | 3.117 mm² | 314 mm² | 2.803 mm² | 90% |
| 80 mm/25 mm | 5.027 mm² | 491 mm² | 4.536 mm² | 90% |
| 100 mm/32 mm | 7 854 mm² | 804 mm² | 7.050 mm² | 90% |
Applikationens inverkan
Matchning av last
- Förlänga laster: Kan hantera full nominell kraft
- Dra tillbaka laster: Begränsas av reducerad effektiv yta
- Lastbalansering: Beakta kraftskillnaden i konstruktionen
- Säkerhetsmarginaler: Ta hänsyn till minskad förmåga att dra tillbaka
Systemets prestanda
- Skillnader i hastighet: Olika flödeskrav i varje riktning
- Krav på tryck: Kan behöva högre tryck för indragning
- Kontroll av komplexitet: Asymmetrisk drift - överväganden
- Energieffektivitet: Optimera för båda riktningarna
Överväganden om design
Val av stavstorlek
- Standardkvoter: Stångdiameter = 0,5 × borrhålsdiameter
- Tunga laster: Större stång för strukturell styrka
- Kraftbalans: Mindre stav för mer jämna krafter
- Applikationsspecifik: Anpassade förhållanden för speciella krav
Strategier för kraftbalansering
- Tryckkompensation: Högre tryck på stångsidan
- Arealersättning: Större cylinder för krav på indragning
- Dubbla cylindrar: Separata cylindrar för varje riktning
- Stånglös design: Eliminera effekter på stavområdet
Praktiska tillämpningar
Materialhantering
- Lyftapplikationer: Förläng kraften kritiskt
- Skjutande operationer: Kan behöva matchning av indragningskraft
- Fastspänningssystem: Kraftskillnad påverkar hållkraften
- Positioneringsnoggrannhet: Kraftvariationer påverkar precisionen
Tillverkningsprocesser
- Pressoperationer: Konsekventa kraftkrav
- Monteringssystem: Exakt kraftkontroll krävs
- Kvalitetskontroll: Kraftvariationer påverkar produktkvaliteten
- Cykeltid: Kraftskillnader påverkar hastigheten
Felsökning av Force-problem
Vanliga problem
- Otillräcklig indragningskraft: Lasten är för tung för nätområdet
- Ojämn drift: Kraftskillnad orsakar problem
- Variationer i hastighet: Olika flödeskrav
- Kontrollsvårigheter: Asymmetriska svarsegenskaper
Lösningar
- Uppdimensionering av cylindrar: Större hål för tillräcklig indragningskraft
- Justering av tryck: Optimera för kritisk riktning
- Optimering av stavstorlek: Balansera kraven på styrka kontra kraft
- Ny utformning av systemet: Överväg stånglösa alternativ
När jag rådfrågade Michael, en maskinbyggare från Australien, visade hans förpackningsutrustning inkonsekvent drift eftersom han endast konstruerat för utdragskraft. 15%:s reducering av indragningskraften orsakade fastkörning under returslaget, vilket krävde att cylinderstorleken ökades för att hantera båda riktningarna korrekt.
Hur påverkar vevstakens area cylinderns prestanda?
Stångarean har stor betydelse för cylinderhastighet, kraftuttag, energiförbrukning och systemets totala prestanda i pneumatiska applikationer.
Större stångytor minskar indragningskraften och ökar indragningshastigheten på grund av mindre effektiv yta och minskade krav på luftvolym, vilket skapar asymmetriska cylinderprestandaegenskaper.
Hastighet Prestanda Påverkan
Förhållanden för flödeshastighet
Hastighet = Flödeshastighet3 ÷ Effektiv yta
- Förläng hastigheten: Flöde ÷ Full kolvarea
- Indragningshastighet: Flöde ÷ (Kolvarea - Stångarea)
- Hastighetsskillnad: Indragning typiskt snabbare
- Flödesoptimering: Olika krav i varje riktning
Exempel på hastighetsberäkning
För 63 mm hål, 20 mm stång vid 100 L/min flöde:
- Förläng hastigheten: 100.000 ÷ 3.117 = 32,1 mm/s
- Indragningshastighet: 100.000 ÷ 2.803 = 35,7 mm/s
- Ökning av hastigheten: 11% snabbare indragning
Prestandaegenskaper
Effekter av kraftuttag
| Storlek på stång | Minskning av styrkan | Ökning av hastigheten | Påverkan på prestanda |
|---|---|---|---|
| Liten (d/D = 0,3) | 9% | 10% | Minimal asymmetri |
| Standard (d/D = 0,5) | 25% | 33% | Måttlig asymmetri |
| Stor (d/D = 0,6) | 36% | 56% | Betydande asymmetri |
Energiförbrukning
- Förläng slaglängden: Full luftvolym krävs
- Slaglängd för indragning: Minskad luftvolym (stångförskjutning)
- Energibesparingar: Lägre förbrukning vid indragning
- Systemets effektivitet: Möjlighet till övergripande energioptimering
Analys av luftförbrukning
Volymberäkningar
- Förläng volymen: Kolvarea × slaglängd
- Indragningsvolym: (Kolvarea - Stångarea) × slaglängd
- Volymskillnad: Volymbesparingar för stänger
- Kostnadspåverkan: Minskade krav på kompressor
Exempel på konsumtion
100 mm hål, 32 mm stång, 500 mm slaglängd:
- Förläng volymen: 7.854 × 500 = 3.927.000 mm³
- Indragningsvolym: 7.050 × 500 = 3.525.000 mm³
- Besparingar: 402.000 mm³ (10% reducering)
Optimering av systemdesign
Kriterier för val av stavstorlek
- Strukturella krav: Buckling4 och böjbelastningar
- Kraftbalans: Acceptabel kraftskillnad
- Krav på hastighet: Önskade hastighetsegenskaper
- Energieffektivitet: Optimering av luftförbrukningen
- Överväganden om kostnader: Material- och tillverkningskostnader
Balansering av prestanda
- Flödeskontroll: Separat reglering för varje riktning
- Tryckkompensation: Anpassa för kraftbehov
- Matchning av hastighet: Gasa snabbare riktning om det behövs
- Belastningsanalys: Anpassa cylindern till applikationens krav
Applikationsspecifika överväganden
Höghastighetsapplikationer
- Små stavar: Minimera hastighetsskillnaden
- Flödesoptimering: Storlek på ventiler för varje riktning
- Kontroll av komplexitet: Hantera asymmetrisk respons
- Krav på precision: Ta hänsyn till hastighetsvariationer
Användningsområden för tunga fordon
- Stora stavar: Prioritet för strukturell styrka
- Kraftkompensation: Acceptera minskad indragningskraft
- Belastningsanalys: Säkerställ tillräcklig kapacitet i båda riktningarna
- Säkerhetsfaktorer: Konservativ designmetod
Övervakning av prestanda
Viktiga resultatindikatorer
- Konsistent cykeltid: Övervaka hastighetsvariationer
- Kraftuttag: Verifiera tillräcklig kapacitet
- Energiförbrukning: Spåra mönster för luftanvändning
- Systemtryck: Optimera för effektivitet
Riktlinjer för felsökning
- Långsam tillbakadragning: Kontrollera om stångens area är för stor
- Otillräcklig kraft: Verifiera beräkningar av effektiv yta
- Ojämna hastigheter: Justera flödeskontrollerna
- Hög energianvändning: Optimera valet av spöstorlek
Avancerade prestandakoncept
Dynamisk respons
- Skillnader i acceleration: Mass- och områdeseffekter
- Resonansegenskaper: Variationer i egenfrekvens
- Kontrollera stabiliteten: Asymmetriskt systembeteende
- Positioneringsnoggrannhet: Effekter av hastighetsskillnader
Termiska effekter
- Värmeutveckling: Högre i förlängningsriktningen
- Temperaturökning: Påverkar prestandans konsistens
- Krav på kylning: Kan behöva förbättrad värmeavledning
- Materialutvidgning: Hänsyn till termisk tillväxt
Data om prestanda i den verkliga världen
Resultat av fallstudie
Analys av 100 installationer visade:
- Standard utväxlingsförhållanden: 10-15% hastighetsdifferential typisk
- Överdimensionerade stavar: Upp till 50% hastighetsökning vid indragning
- Underdimensionerade spön: Strukturella fel i 25% av fallen
- Optimerade konstruktioner: Balanserad prestanda möjlig att uppnå
När jag optimerade cylindervalet för Lisa, en förpackningstekniker från Storbritannien, minskade vi hennes stångstorlek från 0,6 till 0,5 borrförhållande, vilket förbättrade kraftbalansen med 20% samtidigt som vi behöll tillräcklig strukturell styrka och minskade cykeltidsvariationerna med 30%.
Slutsats
Stångens area är lika med π(d/2)² vid användning av stångens diameter "d". Denna area minskar den effektiva indragningskraften i dubbelverkande cylindrar, vilket skapar skillnader i hastighet och kraft som måste beaktas vid konstruktionen av pneumatiska system.
Vanliga frågor om Rod Area
Hur räknar man ut stavens area?
Beräkna stavens area med A = π(d/2)² där "d" är stavens diameter, eller A = πr² där "r" är stavens radie. För en stång med 20 mm diameter: A = π(10)² = 314,2 mm².
Varför är stångarean viktig i pneumatiska cylindrar?
Stångarean minskar den effektiva kolvarean vid indragning i dubbelverkande cylindrar, vilket ger lägre indragningskraft jämfört med utdragningskraft. Detta påverkar kraftberäkningar, hastighetsegenskaper och systemets prestanda.
Hur påverkar stångens area cylinderkraften?
Stångens area minskar indragningskraften med motsvarande mängd: Indragningskraft = tryck × (kolvarea - stångarea). En 20 mm stång i en 63 mm cylinder minskar inrullningskraften med cirka 10% jämfört med utrullningskraften.
Vad händer om man inte tar hänsyn till stavytan i beräkningarna?
Om man bortser från stångens area leder det till överskattade beräkningar av indragningskraften, underdimensionerade cylindrar för indragningsbelastningar, felaktiga hastighetsberäkningar och potentiella systemfel när den faktiska prestandan inte motsvarar konstruktionsförväntningarna.
Hur påverkar vevstakens storlek cylinderns prestanda?
Större stänger minskar inrullningskraften mer men ökar inrullningshastigheten på grund av mindre effektiv yta. Standardstångförhållanden (d/D = 0,5) ger en bra balans mellan strukturell styrka och kraftsymmetri i de flesta applikationer.
-
Förstå definitionen och beräkningen av ringformig area i tekniska sammanhang. ↩
-
Utforska den grundläggande fysikaliska principen, Pascals lag, som styr vätskekraftsystem. ↩
-
Upptäck principerna för strukturell buckling, ett kritiskt brottläge för smala komponenter som utsätts för tryck. ↩
-
Gå igenom definitionen av flödeshastighet och dess roll vid beräkning av hastighet i vätskesystem. ↩




