Kämpar du ständigt med beräkningar av pneumatiska system? Många ingenjörer står inför samma problem när de konstruerar eller felsöker pneumatiska system. Den goda nyheten är att om du behärskar några viktiga ekvationer kan du lösa de flesta av dina pneumatiska utmaningar.
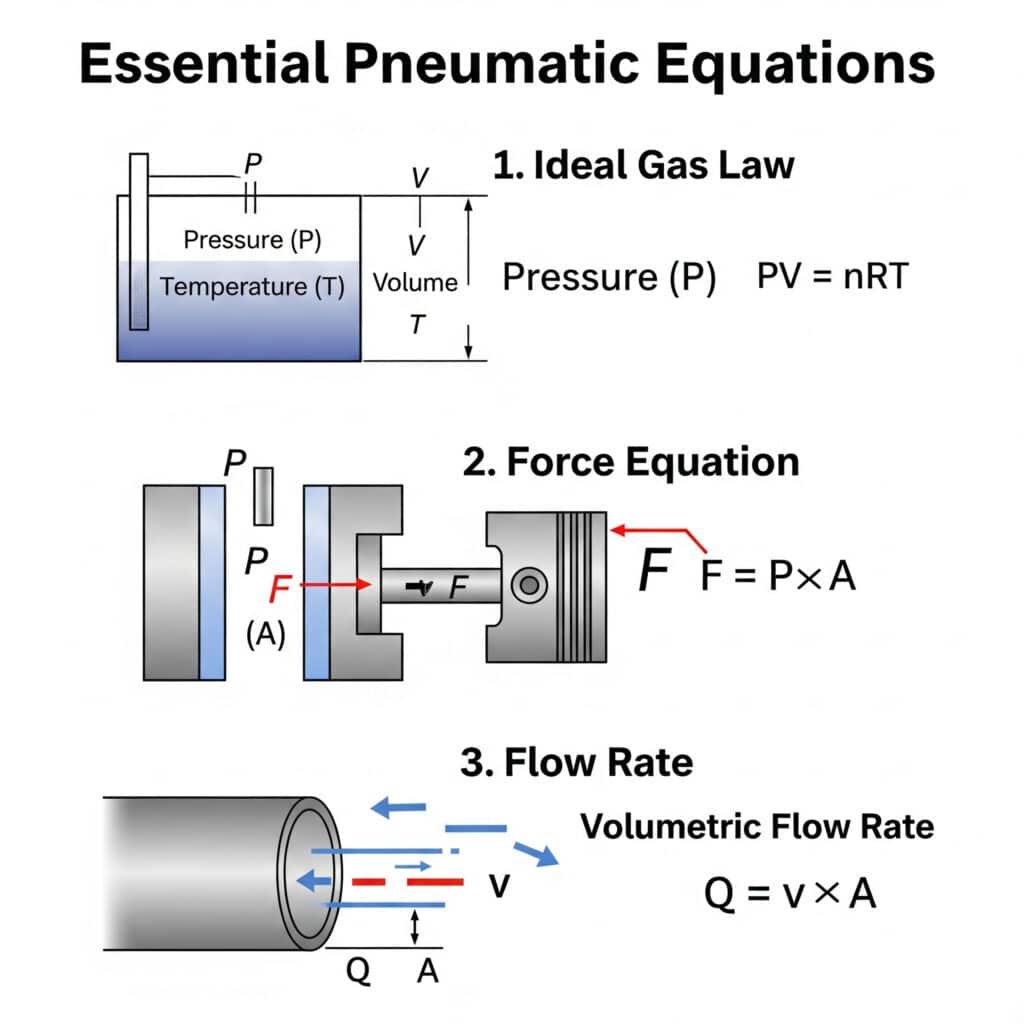
De viktigaste ekvationerna för pneumatisk transmission som alla ingenjörer bör känna till inkluderar ideal gaslag (PV = nRT)1, kraftekvationen (F = P × A) och flödeshastighetssambandet (Q = v × A). Förståelse för dessa grundläggande principer möjliggör korrekt systemdesign och felsökning.
Jag har arbetat med pneumatiska system i över 15 år på Bepto och jag har själv sett hur förståelse för dessa grundläggande ekvationer kan spara tusentals dollar i stilleståndstid och förhindra kostsamma konstruktionsfel.
Innehållsförteckning
- Härledning av gasekvationen: Varför är PV = nRT viktigt i pneumatiska system?
- Hur förhåller sig kraft, tryck och area till varandra i pneumatiska cylindrar?
- Vad är förhållandet mellan flödeshastighet och hastighet i pneumatiska system?
- Slutsats
- Vanliga frågor om ekvationer för pneumatisk transmission
Härledning av gasekvationen: Varför är PV = nRT viktigt i pneumatiska system?
När man konstruerar pneumatiska system är det avgörande att förstå hur gaser beter sig under olika förhållanden. Denna kunskap kan innebära skillnaden mellan ett system som fungerar tillförlitligt och ett som oväntat slutar fungera.
Den ideala gaslagen (PV = nRT) är grundläggande för pneumatiska system eftersom den beskriver hur tryck, volym och temperatur samverkar. Detta förhållande hjälper ingenjörer att förutsäga hur luft kommer att bete sig i stånglösa cylindrar och andra pneumatiska komponenter under varierande driftsförhållanden.

Den ideala gaslagen kan tyckas vara ett teoretiskt begrepp från fysiklektionerna, men den har direkta praktiska tillämpningar i pneumatiska system. Låt mig bryta ner detta till mer praktiska termer.
Förstå variablerna i PV = nRT
| Variabel | Betydelse | Pneumatisk applikation |
|---|---|---|
| P | Tryck | Drifttryck i ditt system |
| V | Volym | Luftkammarens storlek i cylindrar |
| n | Antal mol | Mängden luft i systemet |
| R | Gas konstant2 | Universell konstant (8,314 J/mol-K) |
| T | Temperatur | Driftstemperatur |
Hur temperaturen påverkar pneumatisk prestanda
Temperaturvariationer kan ha en betydande inverkan på pneumatiska systems prestanda. Förra året kontaktade Hans, en av våra kunder i Tyskland, mig med anledning av ojämn prestanda i hans stånglösa cylindersystem. Systemet fungerade perfekt på morgonen, men tappade kraft på eftermiddagen.
Efter att ha analyserat hans installation upptäckte vi att systemet utsattes för direkt solljus, vilket orsakade en temperaturökning på 15°C. Med hjälp av idealgaslagen beräknade vi att denna temperaturförändring orsakade en tryckvariation på nästan 5%. Vi installerade korrekt isolering och problemet löstes omedelbart.
Praktiska tillämpningar av gaslagen inom pneumatisk konstruktion
Vid konstruktion av pneumatiska system med stånglösa cylindrarhjälper gaslagen oss:
- Beräkna tryckförändringar på grund av temperaturfluktuationer
- Bestäm volymkrav för luftbehållare
- Förutse variationer i kraftuttag under olika förhållanden
- Dimensionera kompressorer på lämpligt sätt för applikationen
Hur förhåller sig kraft, tryck och area till varandra i pneumatiska cylindrar?
Att förstå sambandet mellan kraft, tryck och area är avgörande när du ska välja rätt stångfri cylinder för din applikation. Denna kunskap säkerställer att du får den prestanda du behöver utan att spendera för mycket.
Den Förhållandet kraft-tryck-area3 i pneumatiska cylindrar definieras av F = P × A, där F är kraft (N), P är tryck (Pa) och A är den effektiva ytan (m²). Denna ekvation gör det möjligt för ingenjörer att beräkna den exakta kraften hos stånglösa cylindrar vid olika drifttryck.
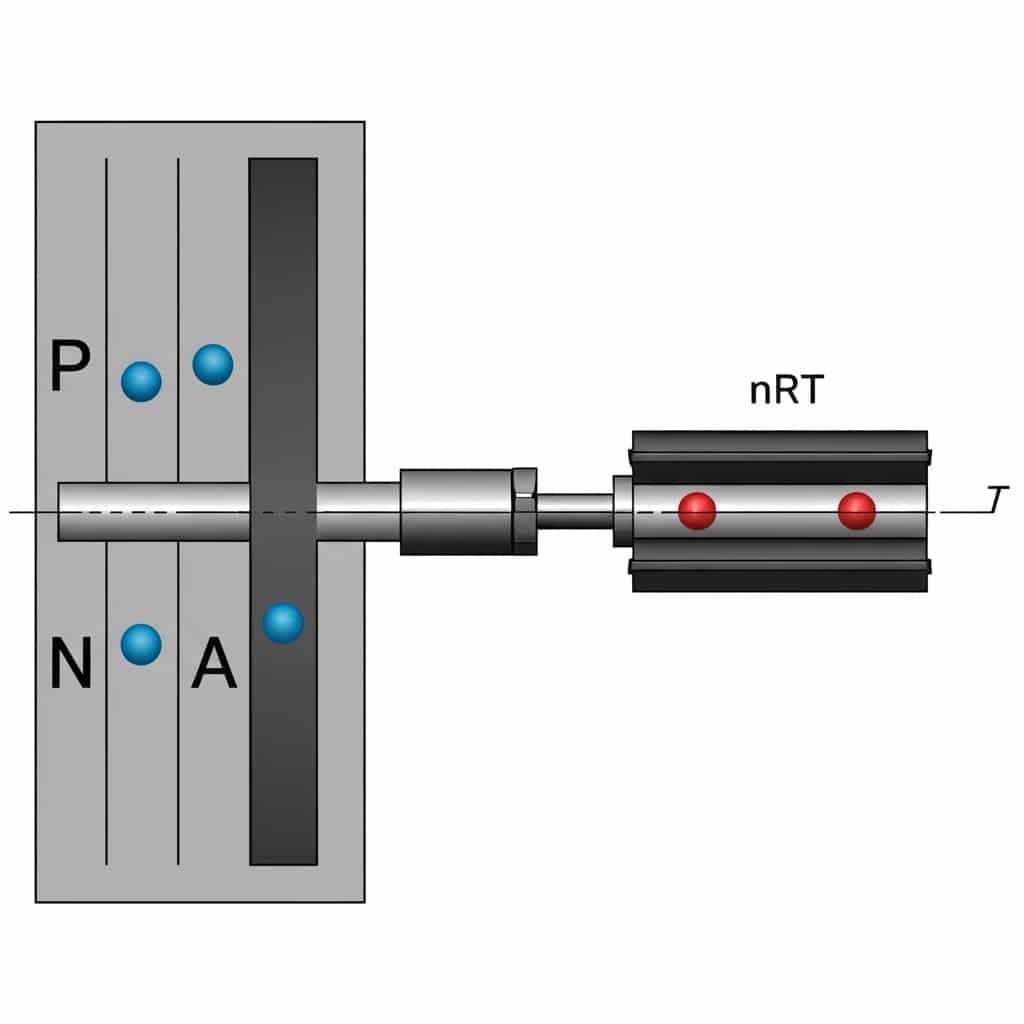
Denna enkla ekvation är grunden för alla pneumatiska kraftberäkningar, men det finns flera praktiska överväganden som många ingenjörer förbiser.
Beräkningar av effektiv yta för olika cylindertyper
Det effektiva området varierar beroende på cylindertyp:
| Cylindertyp | Beräkning av effektiv yta | Anteckningar |
|---|---|---|
| Enkelverkande | A = πr² | Fullt borrningsområde |
| Dubbelverkande (förlängning) | A = πr² | Fullt borrningsområde |
| Dubbelverkande (tillbakadragning) | A = π(r² - r'²) | r' är stavens radie |
| Stånglös cylinder | A = πr² | Konsekvent i båda riktningarna |
Faktorer för styrkeeffektivitet i verkliga världen
I praktiken påverkas den faktiska kraftutmatningen av:
- Friktionsförluster: Typiskt 3-20% beroende på tätningens utformning
- Tryckfall: Kan minska det effektiva trycket med 5-10%
- Dynamiska effekter: Accelerationskrafter kan minska tillgänglig kraft
Jag minns att jag arbetade med Sarah, en maskiningenjör från ett förpackningsföretag i Storbritannien. Hon höll på att konstruera en ny maskin och hade räknat ut att hon behövde en stånglös cylinder med 63 mm hål för att uppnå den kraft som krävdes. Hon hade dock inte räknat med friktionsförluster.
Vi rekommenderade att öka till en cylinder med 80 mm borrning, vilket gav tillräckligt med extra kraft för att övervinna friktionen samtidigt som den önskade prestandan bibehölls. Den här enkla justeringen besparade henne en kostsam omkonstruktion efter installationen.
Jämförelse mellan teoretisk och faktisk kraftutmatning
Vid val av stånglösa cylindrar rekommenderar jag alltid:
- Beräkna den teoretiska kraften med F = P × A
- Använd en säkerhetsfaktor på 25% för de flesta applikationer
- Verifiera beräkningarna med faktiska prestandauppgifter från tillverkaren
- Beakta dynamiska belastningsförhållanden i tillämpliga fall
Vad är förhållandet mellan flödeshastighet och hastighet i pneumatiska system?
Flödeshastighet och hastighet är kritiska parametrar som avgör hur snabbt ditt pneumatiska system reagerar. Genom att förstå detta förhållande kan du förhindra trög prestanda och säkerställa att ditt system uppfyller kraven på cykeltid.
Förhållandet mellan flödeshastighet (Q) och hastighet (v)4 i pneumatiska system definieras av Q = v × A, där Q är det volumetriska flödet, v är lufthastigheten och A är tvärsnittsarean i passagen. Denna ekvation är avgörande för att dimensionera luftledningar och ventiler på rätt sätt.
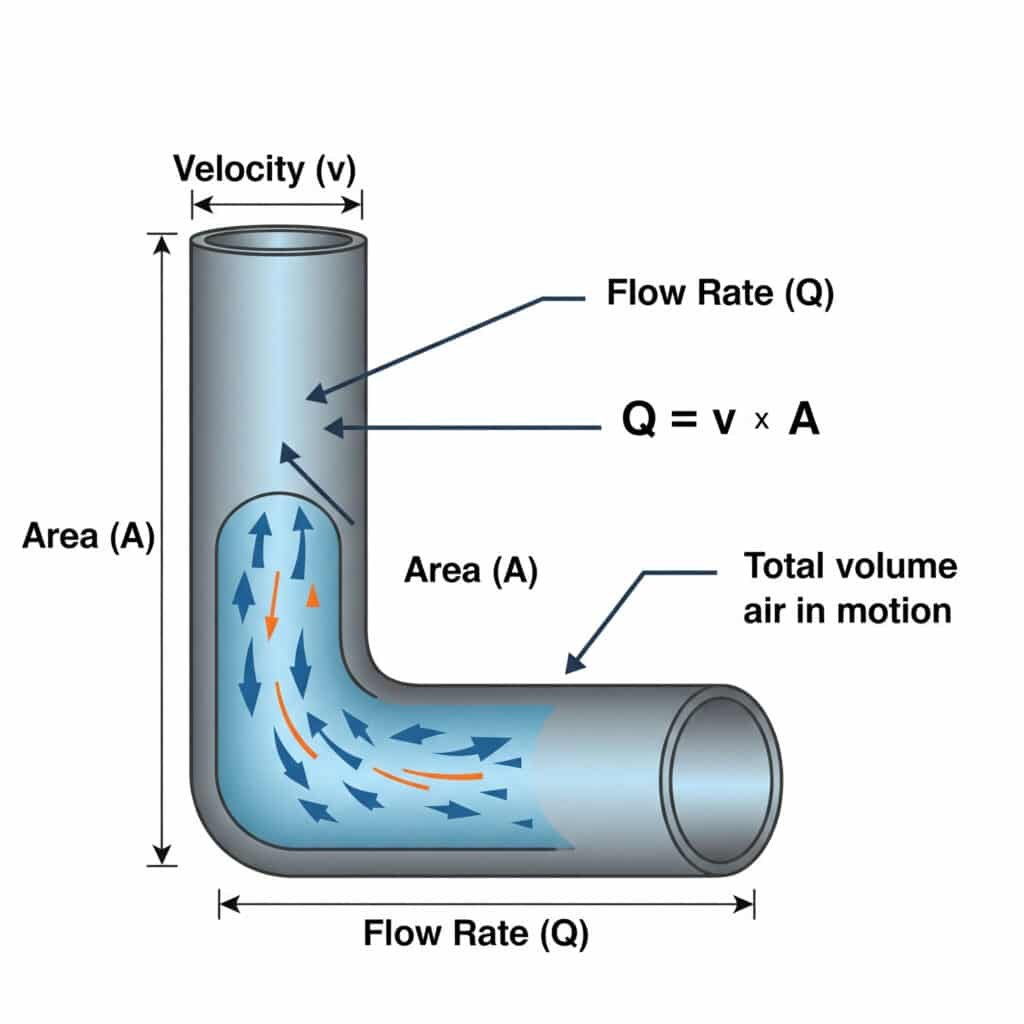
Många problem med pneumatiska system beror på felaktig dimensionering av luftförsörjningskomponenter. Låt oss undersöka hur den här ekvationen påverkar prestandan i verkligheten.
Kritiska flödeshastigheter för vanliga pneumatiska komponenter
Olika komponenter har olika flödeskrav:
| Komponent | Typiskt krav på flödeshastighet | Konsekvenser av underdimensionering |
|---|---|---|
| Stånglös cylinder (25 mm hål) | 15-30 l/min | Långsam drift, minskad kraft |
| Stånglös cylinder (63 mm borrning) | 60-120 L/min | Inkonsekvent rörelse |
| Riktad styrventil | Varierar beroende på storlek | Tryckfall, långsam respons |
| Luftbehandlingsenhet | System totalt + 30% | Tryckfluktuationer |
Hur rördiametern påverkar systemets prestanda
Luftledningarnas diameter har en dramatisk effekt på systemets prestanda:
- Tryckfall: Ökar med kvadraten på hastigheten
- Svarstid: Mindre linjer innebär högre hastighet men mer motstånd
- Energieffektivitet: Större ledningar minskar tryckfallet men ökar kostnaden
Beräkning av rätt ledningsdimensioner för pneumatiska system
För korrekt dimensionering av luftledningar för din stånglösa cylinderapplikation:
- Bestäm erforderligt flöde baserat på cylinderstorlek och cykeltid
- Beräkna det maximalt tillåtna tryckfallet (normalt 0,1 bar eller mindre)
- Välj en lindiameter som håller hastigheten under 15-20 m/s
- Verifiera ventilens flödeskapacitet (Cv- eller Kv-värde5) motsvarar systemkraven
En gång hjälpte jag en kund i Frankrike som hade problem med långsam cylinderrörelse trots att han hade en stor kompressor. Problemet var inte otillräcklig luftgenerering - det var att hans 6 mm slangar skapade för stort motstånd. En uppgradering till 10 mm-ledningar löste problemet omedelbart och ökade maskinens cykelhastighet med 40%.
Slutsats
Förståelse för dessa tre grundläggande pneumatiska ekvationer - den ideala gaslagen, förhållandet mellan kraft, tryck och area samt sambandet mellan flödeshastighet och hastighet - utgör grunden för en framgångsrik design av pneumatiska system. Genom att tillämpa dessa principer kan du välja rätt komponenter till stånglösa cylindrar, felsöka problem på ett effektivt sätt och optimera systemets prestanda.
Vanliga frågor om ekvationer för pneumatisk transmission
Vad är den ideala gaslagen och varför är den viktig för pneumatiska system?
Den ideala gaslagen (PV = nRT) beskriver hur tryck, volym, temperatur och gasmängd förhåller sig till varandra i ett pneumatiskt system. Den är viktig eftersom den hjälper ingenjörer att förutse hur förändrade förhållanden (särskilt temperatur) kommer att påverka systemets prestanda och tryckkrav.
Hur beräknar jag kraftuttaget hos en cylinder utan stång?
Beräkna den utgående kraften genom att multiplicera trycket med den effektiva ytan (F = P × A). För en stångfri cylinder är den effektiva ytan densamma i båda riktningarna, vilket gör kraftberäkningen enklare än för konventionella cylindrar som har olika utdrags- och indragningskrafter.
Vad är skillnaden mellan flödeshastighet och hastighet i pneumatiska system?
Flödeshastigheten är den volym luft som rör sig genom ett system per tidsenhet (vanligtvis i l/min), medan hastigheten är den hastighet med vilken luften rör sig genom en passage (i m/s). De hänger ihop enligt ekvationen Q = v × A, där A är passagens tvärsnittsarea.
Hur påverkar temperaturen prestandan hos pneumatiska system?
Temperaturen påverkar trycket direkt enligt den ideala gaslagen. En temperaturökning på 10°C kan öka trycket med cirka 3,5% om volymen förblir konstant. Detta kan orsaka tryckvariationer, påverka tätningarnas prestanda och förändra kraftuttaget i stånglösa cylindrar.
Vilken är den vanligaste orsaken till tryckfall i pneumatiska system?
De vanligaste orsakerna till tryckfall är underdimensionerade luftledningar, begränsande kopplingar och otillräcklig flödeskapacitet hos ventilerna. Enligt ekvationen för flödeshastighet kräver mindre passager högre lufthastighet, vilket ökar motståndet och tryckfallet exponentiellt.
Hur dimensionerar jag luftledningarna rätt för en stånglös cylinder?
Dimensionera luftledningarna genom att beräkna erforderligt flöde baserat på cylindervolym och cykeltid och välj sedan en ledningsdiameter som håller lufthastigheten under 15-20 m/s för att minimera tryckfallet. För de flesta applikationer med stånglösa cylindrar ger 8-12 mm luftledningar en bra balans mellan prestanda och kostnad.
-
Ger en detaljerad förklaring av idealgaslagen, den grundläggande tillståndsekvationen för en hypotetisk idealgas som approximerar beteendet hos många gaser under olika förhållanden. ↩
-
Förklarar rollen och värdet av den universella gaskonstanten (R) i den ideala gaslagen, som fungerar som en fysikalisk konstant som kopplar samman energiskalor med temperaturskalor. ↩
-
Ger en grundläggande förklaring av tryck, definierat som den kraft som appliceras vinkelrätt mot ytan på ett föremål per ytenhet över vilken kraften är fördelad. ↩
-
Redogör för kontinuitetsekvationen, ett grundläggande begrepp inom strömningslära som säger att för en inkompressibel vätska måste massflödet vara konstant från ett tvärsnitt av ett rör till ett annat. ↩
-
Ger en teknisk definition av flödeskoefficient (Cv) och flödesfaktor (Kv), som är standardiserade värden som används för att jämföra flödeskapaciteten hos olika ventiler. ↩


