Pnömatik sistemlerinizde yavaş silindir hızları, tutarsız hareket veya yetersiz kuvvetle mi mücadele ediyorsunuz? Bu yaygın sorunlar genellikle yanlış anlaşılan bir suçludan kaynaklanır: akış direnci. Birçok mühendis, pnömatik bileşenlerini yalnızca basınç ve kuvvet gereksinimlerine göre boyutlandırır ve akış direncinin gerçek dünya performansı üzerindeki kritik etkisini göz ardı eder.
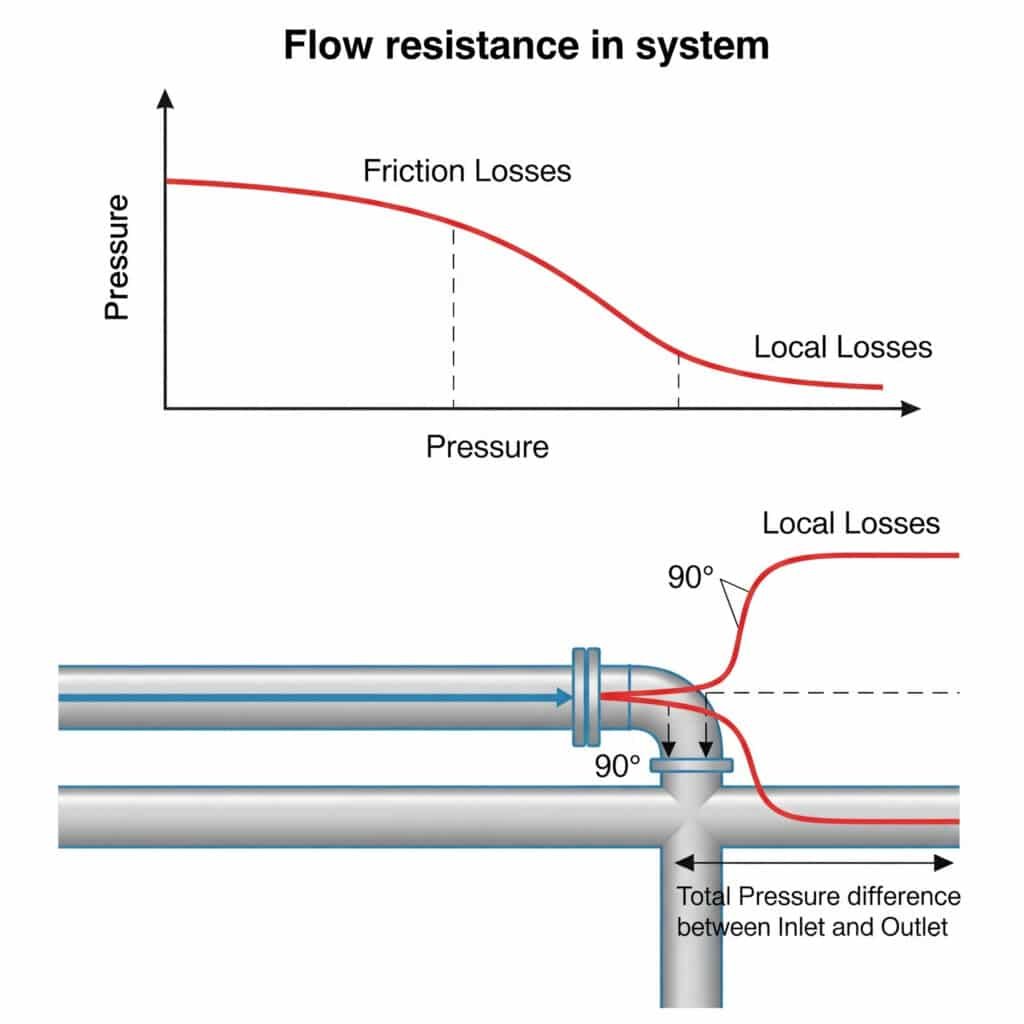
Pnömatik sistemlerdeki akış direnci, mevcut kuvveti azaltan, maksimum hızı sınırlayan ve tutarsız harekete neden olan basınç düşüşleri yaratır. Bu direnç hem düz borulardaki sürtünmeden (sürtünme kayıpları) hem de bağlantı parçaları, dirsekler ve valflerdeki kesintilerden (yerel kayıplar) kaynaklanır. Bu dirençler birlikte, gerçek sistem performansını teorik hesaplamalara kıyasla 20-50% azaltabilir.
Bepto'da pnömatik sistemlerle çalıştığım 15 yılı aşkın süre boyunca, akış direncinin anlaşılması ve ele alınmasının düşük performanslı sistemleri güvenilir ve verimli operasyonlara dönüştürdüğü sayısız vaka gördüm. Bu gizli performans katillerini hesaplama ve en aza indirme konusunda öğrendiklerimi paylaşmama izin verin.
İçindekiler
- Pnömatik Hatlardaki Sürtünme Kayıplarını Gerçekte Nasıl Hesaplarsınız?
- Eşdeğer Uzunluk Yöntemi Doğru Sistem Tasarımı İçin Neden Kritiktir?
- Hava Azaltılmış Delik Kesitlerinden Geçtiğinde Ne Olur?
- Sonuç
- Pnömatik Sistemlerde Akış Direnci Hakkında SSS
Pnömatik Hatlardaki Sürtünme Kayıplarını Gerçekte Nasıl Hesaplarsınız?
Düz boru ve tüplerdeki sürtünme kayıpları, akış direnci hesaplamalarının temelini oluşturur, ancak birçok mühendis, sistemlerin yetersiz boyutlandırılmasına yol açan aşırı basitleştirilmiş temel kurallara güvenmektedir.
Pnömatik hatlardaki sürtünme kayıpları aşağıdaki formül kullanılarak hesaplanır Darcy-Weisbach denklemi1: ΔP = λ(L/D)(ρv²/2), burada λ sürtünme faktörü, L boru uzunluğu, D boru çapı, ρ hava yoğunluğu ve v akış hızıdır. Pnömatik sistemler için sürtünme faktörü λ aşağıdakilere bağlı olarak değişir Reynolds sayısı2 ve bağıl pürüzlülük ile belirlenir ve tipik olarak arama tabloları veya Moody diyagramı3.
Sürtünme kayıplarını anlamanın sistem tasarımı ve sorun giderme için pratik sonuçları vardır. Bunu uygulanabilir içgörülere ayırmama izin verin.
Sürtünme Faktörü Tablolarının Etkin Kullanımı
Sürtünme faktörü (λ) basınç düşüşlerinin hesaplanmasında anahtar parametredir, ancak değerinin belirlenmesi akış koşullarının dikkate alınmasını gerektirir:
| Akış Rejimi | Reynolds Sayısı (Re) | Sürtünme Faktörü Belirleme |
|---|---|---|
| Laminer Akış | Yeniden < 2000 | λ = 64/Re |
| Geçiş Akışı | 2000 < Re < 4000 | Güvenilmez - bu aralıkta tasarım yapmaktan kaçının |
| Türbülanslı Akış | Re > 4000 | Bağıl pürüzlülüğe (ε/D) dayalı arama tablolarını kullanın |
Pratik Sürtünme Faktörü Arama Tablosu
Pnömatik sistemlerdeki türbülanslı akış için bu basitleştirilmiş tabloyu kullanın:
| Boru Malzemesi | Bağıl Pürüzlülük (ε/D) | Yaygın Reynolds Sayılarında Sürtünme Faktörü (λ) |
|---|---|---|
| Re = 10,000 | ||
| Düz Boru (PVC, Poliüretan) | 0.0001 – 0.0005 | 0.031 |
| Alüminyum Boru | 0.001 – 0.002 | 0.035 |
| Galvanizli Çelik | 0.003 – 0.005 | 0.042 |
| Paslı Çelik | 0.01 – 0.05 | 0.054 |
Gerçek Pnömatik Sistemlerde Basınç Düşüşünün Hesaplanması
Pratik bir örnek üzerinden yürüyelim:
| Parametre | Değer/Hesaplama | Örnek |
|---|---|---|
| Boru Çapı (D) | İç çap | 8mm (0.008m) |
| Boru Uzunluğu (L) | Toplam düz uzunluk | 5m |
| Akış Hızı (Q) | Sistem gereksinimlerinden | 20 standart litre/saniye |
| Hava Yoğunluğu (ρ) | Çalışma basıncında | 6 bar'da 7,2 kg/m³ |
| Akış Hızı (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Reynolds Sayısı (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1.273.600 |
| Bağıl Pürüzlülük | Poliüretan borular için | 0.0003 |
| Sürtünme Faktörü (λ) | Arama tablosundan | 0.017 |
| Basınç Düşüşü (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0.017×(5/0.008)×(7.2×398²/2) = 6.07 bar |
Gerçek Dünya Uygulaması: Silindir Hızı Sorunlarının Çözümü
Geçen yıl Wisconsin'de bir paketleme ekipmanı şirketinde üretim mühendisi olan Sarah ile çalıştım. Çubuksuz silindir sistemi, doğru boyutta silindire ve yeterli besleme basıncına sahip olmasına rağmen beklenen hızın yalnızca 60%'sinde çalışıyordu.
Sistemini analiz ettikten sonra, yüksek akışlı bir uygulama için 6 mm boru kullandığını keşfettim. Sürtünme kayıpları 2,1 bar basınç düşüşüne neden olarak mevcut gücü ve hızı önemli ölçüde azaltıyordu. Boruları 10 mm'ye yükselterek basınç düşüşünü 0,4 bar'a indirdik ve sistemi başka hiçbir değişiklik yapmadan gerekli performansı hemen elde etti.
Gerçek Sistemlerde Sürtünme Kayıplarını Etkileyen Faktörler
Gerçek sürtünme kayıplarını etkileyen çeşitli faktörler vardır:
- Hava sıcaklığı: Daha yüksek sıcaklıklar viskoziteyi ve sürtünmeyi artırır
- Kirlenme: Kir ve yağ etkili pürüzlülüğü artırabilir
- Boru bükme: Bükülmüş borulardaki mikro deformasyon direnci artırır
- Yaş bozulmaları: Korozyon ve birikintiler zamanla pürüzlülüğü artırır
- Çalışma basıncı: Daha yüksek basınçlar yoğunluğu ve kayıpları artırır
Eşdeğer Uzunluk Yöntemi Doğru Sistem Tasarımı İçin Neden Kritiktir?
Bağlantı parçaları, vanalar ve dirseklerdeki yerel kayıplar genellikle düz borulardaki sürtünme kayıplarını aşar, ancak birçok mühendis bunları ya görmezden gelir ya da performans sorunlarına yol açan kaba tahmin yöntemleri kullanır.
Eşdeğer uzunluk yöntemi, bağlantı parçaları ve vanalardan kaynaklanan yerel kayıpları, aynı basınç düşüşüne neden olacak eşdeğer bir düz boru uzunluğuna dönüştürür. Bu, Le = K(D/λ) kullanılarak hesaplanır; burada Le eşdeğer uzunluk, K yerel kayıp katsayısı4D boru çapı ve λ sürtünme faktörüdür. Bu yöntem hesaplamaları basitleştirir ve daha doğru sistem performansı tahminleri sağlar.
Bu yöntemin pnömatik sistem tasarımında nasıl etkili bir şekilde uygulanacağını inceleyelim.
Yaygın Pnömatik Bileşenler için Eşdeğer Uzunluk Tabloları
İşte yaygın pnömatik bileşenler için pratik bir referans tablosu:
| Bileşen | K-Değeri | Eşdeğer Uzunluk (Le/D) |
|---|---|---|
| 90° Dirsek (keskin) | 0.9 | 30 |
| 90° Dirsek (standart yarıçap) | 0.3 | 10 |
| 45° Dirsek | 0.2 | 7 |
| T-Kavşağı (içinden akış) | 0.3 | 10 |
| T-Kavşağı (branşman akışı) | 1.0 | 33 |
| Küresel Vana (tamamen açık) | 0.1 | 3 |
| Sürgülü Vana (tamamen açık) | 0.2 | 7 |
| Hızlı Bağlantı Kaplini | 0.4-0.8 | 13-27 |
| Çek Valf | 1.5-2.5 | 50-83 |
| Standart Akış Kontrol Vanası | 1.0-3.0 | 33-100 |
Eşdeğer Uzunluk Yönteminin Uygulanması
Bu yöntemi etkili bir şekilde kullanmak için:
- Pnömatik devrenizdeki tüm bileşenleri tanımlayın
- Her bir bileşen için K değerini veya eşdeğer uzunluk oranını (Le/D) bulun
- Boru çapı ile çarparak eşdeğer uzunluğu hesaplayın
- Tüm eşdeğer uzunlukları gerçek düz boru uzunluğuna ekleyin
- Sürtünme kaybı hesaplamalarınızda toplam etkin uzunluğu kullanın
Örneğin, 5 m düz 8mm boru artı dört 90° dirsek, bir T-bağlantısı ve iki hızlı bağlantı içeren bir sistem:
| Bileşen | Miktar | Le/D | Eşdeğer Uzunluk |
|---|---|---|---|
| 90° Dirsekler | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| T-Kavşağı | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Hızlı Bağlantılar | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Toplam Eşdeğer Uzunluk | 0.72m | ||
| Gerçek Düz Uzunluk | 5.00m | ||
| Toplam Etkin Uzunluk | 5.72m |
Bu, 5m'lik sisteminizin yerel kayıplar nedeniyle aslında 5,72m'lik bir sistem gibi davrandığı anlamına gelir - etkin uzunlukta 14,4%'lik bir artış.
Örnek Olay İncelemesi: Montaj Sistemlerinde Valf Yerleşimini Optimize Etme
Kısa bir süre önce Arizona'daki bir elektronik montaj tesisinde otomasyon mühendisi olan Miguel'e yardım ettim. Pick-and-place sistemi, yüksek kaliteli bileşenler kullanmasına rağmen tutarsız hareket ve döngü süresi değişimleri yaşıyordu.
Analiz, valf manifoldunun silindirlerden 3 m uzakta olduğunu ve devrenin çok sayıda bağlantı parçası içerdiğini ortaya koydu. Eşdeğer uzunluk hesaplaması, 3 m'lik gerçek mesafenin yerel kayıplar nedeniyle 7,2 m'lik bir etkin uzunluğa sahip olduğunu gösterdi - düz boru mesafesinin iki katından fazla!
Valf manifoldunu silindirlere daha yakın bir yere yerleştirerek ve birkaç bağlantı parçasını ortadan kaldırarak etkin uzunluğu 7,2 m'den 2,1 m'ye düşürdük. Bu, basınç düşüşünü 70% azaltarak tutarlı hareket ve döngü süresinde 15% azalma sağladı.
Yerel Kayıpları En Aza İndirmek için Pratik İpuçları
Pnömatik sistemlerinizdeki yerel kayıpları azaltmak için:
- Süpürülmüş veya yuvarlatılmış dirsekler kullanın keskin kıvrımlar yerine (K-değerini 67% azaltır)
- Bağlantı parçalarının sayısını en aza indirin daha doğrudan rota planlayarak
- Düşük sürtünmeli bileşenler seçin uygun yerlerde tam delikli küresel vanalar gibi
- Bağlantı parçalarını doğru boyutlandırın - küçük boyutlu bağlantı parçaları orantısız kayıplara neden olur
- Vanaları aktüatörlere yakın yerleştirin etkin hortum uzunluğunu en aza indirmek için
Hava Azaltılmış Delik Kesitlerinden Geçtiğinde Ne Olur?
Pnömatik devrelerdeki kısmi kapalı valfler, küçük boyutlu bağlantı parçaları veya çap geçişleri gibi azaltılmış delik bölümleri, sistem performansını ciddi şekilde etkileyebilecek önemli akış kısıtlamaları yaratır.
Hava azaltılmış delik bölümlerinden aktığında, basınç düşüşleri5 ΔP = ρ(v₂² - v₁²)/2 formülüne göre meydana gelir; burada v₁ kısıtlamadan önceki hız ve v₂ kısıtlamadaki hızdır. Bu durum, C = (1 - (d/D)⁴) delik oranı dengeleme faktörü kullanılarak telafi edilebilir; burada d küçültülmüş çap ve D orijinal çaptır. Bu faktör, gerçek sistem performansını tahmin etmeye ve bileşenlerin yetersiz boyutlandırılmasını önlemeye yardımcı olur.
Küçültülmüş delik kesitlerinin pratik sonuçlarını ve sistem tasarımında bunların nasıl hesaba katılacağını inceleyelim.
Çap Geçişlerindeki Basınç Düşüşlerinin Hesaplanması
Hava daha büyük bir çaptan daha küçük bir çapa aktığında, basınç düşüşü kullanılarak hesaplanabilir:
| Parametre | Formül | Örnek |
|---|---|---|
| Orijinal Çap (D) | Spesifikasyonlardan | 10mm |
| Azaltılmış Çap (d) | Spesifikasyonlardan | 6mm |
| Delik Oranı (d/D) | Basit bölme | 0.6 |
| Akış Hızı (Q) | Sistem gereksinimlerinden | 15 standart litre/saniye |
| Orijinal Borudaki Hız (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| İndirgenmiş Kesitteki Hız (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Basınç Düşüşü (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Tazminat Faktörü (C) | C = (1 - (d/D)⁴) | 0.87 |
Yaygın Delik Azaltma Senaryoları ve Etkileri
İşte farklı delik küçültmelerinin akış kapasitesini nasıl etkilediği:
| Delik Küçültme | Akış Kapasitesi Azaltımı | Basınç Düşüşü Artışı |
|---|---|---|
| 10 mm ila 8 mm | 36% | 2.4× |
| 10 mm ila 6 mm | 64% | 7.7× |
| 10 mm ila 4 mm | 84% | 39× |
| 8mm ila 6mm | 44% | 3.2× |
| 8mm ila 4mm | 75% | 16× |
| 6mm ila 4mm | 56% | 5.1× |
Bu rakamlar, çapta küçük görünen azalmaların sistem performansı üzerinde neden dramatik etkileri olabileceğini vurgulamaktadır.
Çoklu Kısıtlamaların Kümülatif Etkisi
Gerçek pnömatik devrelerde, seri olarak birden fazla kısıtlama meydana gelir. Bunların etkisi kümülatiftir ve kullanılarak hesaplanabilir:
- Her bir kısıtlamayı eşdeğer C-faktörüne dönüştürün
- Toplam C-faktörünü hesaplayın: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Genel sistem performansı düşüşünü belirlemek için bu toplam faktörü kullanın
Örnek Olay İncelemesi: Valf-Aktüatör Uyumsuzluğu Sorunlarının Çözümü
Geçen ay, Kuzey Carolina'da bir mobilya üretim tesisinde bakım şefi olan Thomas ile çalıştım. Yeni rotsuz silindir sistemi, üreticinin tavsiye ettiği vana boyutunu kullanmasına rağmen beklenen hızın yarısından daha az bir hızda çalışıyordu.
Yapılan incelemede devresinde birden fazla delik azalması tespit edilmiştir:
- 8mm vana portlarına 10mm besleme hattı (C₁ = 0.36)
- 8mm valf bağlantı noktalarından 6mm bağlantı parçalarına (C₂ = 0.44)
- Dahili kısıtlamalı 8mm silindir portlarına 6mm bağlantı parçaları (C₃ = 0.32)
Toplam telafi faktörü Ctotal = 1 - (1-0.36)(1-0.44)(1-0.32) = 0.75 idi, yani sistemi teorik akış kapasitesinin 75%'sini kaybediyordu!
Sistem genelinde uygun boyutta bileşenlere yükseltme yaparak bu kısıtlamaları ortadan kaldırdık ve silindir veya besleme basıncını değiştirmeden gerekli performansı elde ettik.
Delik Küçültme Kayıplarını En Aza İndirmek için Pratik Stratejiler
Delik azalmalarından kaynaklanan kayıpları azaltmak için:
- Bileşenleri tutarlı şekilde boyutlandırın pnömatik devre boyunca
- En büyük pratik boru boyutunu kullanın yüksek akışlı uygulamalar için
- Dahili bileşen kısıtlamalarına dikkat edinsadece bağlantı boyutları değil
- Paralel akış yollarını göz önünde bulundurun yüksek akış gereksinimleri için
- Gereksiz adaptörleri ve geçişleri ortadan kaldırın mümkün olan her yerde
Pnömatik Sistemlerde "En Zayıf Halka" Prensibi
Pnömatik sisteminizin performansının en kısıtlayıcı bileşeni ile sınırlı olduğunu unutmayın. Tek bir küçük boyutlu eleman, sistemin başka yerlerinde doğru boyutlandırılmış bileşenlerin faydalarını ortadan kaldırabilir.
Örneğin, 10 mm boru, 10 mm valfler, ancak silindirde 6 mm bağlantı parçaları bulunan bir sistem, daha yüksek bir maliyetle, baştan sona 6 mm bileşenlere sahip bir sistemle esasen aynı performansı gösterecektir.
Sonuç
Sürtünme faktörü tabloları, eşdeğer uzunluk yöntemleri ve azaltılmış delik telafisi yoluyla akış direncini anlamak ve doğru şekilde hesaplamak, gerçek dünya koşullarında beklendiği gibi performans gösteren pnömatik sistemler tasarlamak için çok önemlidir. Bu hesaplama yöntemlerini ve tasarım ilkelerini uygulayarak, kolsuz silindir uygulamalarınızı ve diğer pnömatik sistemlerinizi maksimum performans ve güvenilirlik için optimize edebilirsiniz.
Pnömatik Sistemlerde Akış Direnci Hakkında SSS
Pnömatik bir sistemde ne kadar basınç düşüşü kabul edilebilir?
Kabul edilebilir basınç düşüşü uygulama gereksinimlerinize bağlıdır, ancak genel bir kılavuz olarak, verimli çalışma için toplam basınç düşüşünü besleme basıncının 10-15%'si ile sınırlayın. 6 barlık bir sistem için bu, toplam basınç düşüşünü 0,6-0,9 barın altında tutmak anlamına gelir. Kritik uygulamalar, tutarlı performansı korumak için 5-8% gibi daha düşük basınç düşüşleri gerektirebilir.
Boru çapı ile basınç düşüşü arasındaki ilişki nedir?
Basınç düşüşü, pnömatik sistemlerdeki türbülanslı akış için çapın (D⁵) beşinci kuvvetiyle ters orantılıdır. Bu, boru çapının iki katına çıkarılmasının basınç düşüşünü yaklaşık 32 kat azalttığı anlamına gelir. Örneğin, boru çapının 6 mm'den 12 mm'ye çıkarılması, aynı akış koşulları altında basınç düşüşünü 1,5 bar'dan sadece 0,047 bar'a düşürebilir.
Pnömatik uygulamam için doğru boru boyutunu nasıl belirleyebilirim?
Akış hızı gereksinimlerine ve kabul edilebilir basınç düşüşüne göre boru boyutunu seçin. Reynolds sayısını ve sürtünme faktörünü hesaplayın, ardından farklı çaplar için basınç düşüşünü belirlemek üzere Darcy-Weisbach denklemini kullanın. Alan kısıtlamalarını ve maliyeti göz önünde bulundururken basınç düşüşünü kabul edilebilir sınırlar içinde (tipik olarak besleme basıncının <10%'si) tutan en küçük çapı seçin.
Hangisi daha fazla kısıtlama yaratır: 90° dirsek mi yoksa 5 metre düz boru mu?
Keskin bir 90° dirsek tipik olarak 30 boru çapındaki düz boruya eşdeğer direnç oluşturur. 8mm boru için, bir keskin dirsek yaklaşık 240mm (30 × 8mm) düz boruya eşittir. Bu da 5 metrelik düz borunun tek bir dirsekten yaklaşık 21 kat daha fazla kısıtlama yarattığı anlamına gelir. Bununla birlikte, sistemler genellikle kümülatif etkisi düz uzunluktaki kayıpları aşabilen birden fazla dirsek ve bağlantı parçası içerir.
Hızlı bağlantı parçaları sistem performansını nasıl etkiler?
Standart hızlı bağlantı parçaları tipik olarak 15-25 boru çapındaki düz boruya eşdeğer bir yerel kayba yol açar. Daha da önemlisi, birçok hızlı bağlantı, nominal boyutlarından daha küçük iç kısıtlamalara sahiptir. "10 mm" hızlı bağlantı sadece 7-8 mm'lik bir iç kısıtlamaya sahip olabilir ve bu noktada akış kapasitesini 50-70% azaltabilecek bir delik azalması yaratır.
Kısmen kapalı akış kontrol vanalarının sistem performansı üzerindeki etkisi nedir?
Tam delik alanının 50%'sine kadar kapatılan bir akış kontrol vanası akışı sadece 50% azaltmaz, çap ve akış kapasitesi arasındaki doğrusal olmayan ilişki nedeniyle akışı yaklaşık 75% azaltır. Basınç düşüşü hız değişiminin karesine göre artar, bu nedenle etkin çapı yarıya indirmek aynı akış koşulları altında basınç düşüşünü yaklaşık 16 kat artırır.
-
Bir borudaki sürtünmeden kaynaklanan basınç kaybını hesaplamak için akışkanlar dinamiğinde temel ve yaygın olarak kullanılan bir formül olan Darcy-Weisbach denkleminin ayrıntılı bir dökümünü sağlar. ↩
-
Farklı akışkan akışı durumlarında akış modellerini (laminer veya türbülanslı) tahmin etmek için kullanılan kritik bir boyutsuz büyüklük olan Reynolds sayısının net bir tanımını sunar. ↩
-
Darcy sürtünme faktörünü Reynolds sayısı ve bağıl pürüzlülüğe karşı çizen kapsamlı bir grafik olan ve mühendislerin borulardaki basınç düşüşünü belirlemeleri için standart bir araç olan Moody diyagramını sunar. ↩
-
Eşdeğer uzunluk yönteminin bir parçası olarak bir boru bağlantı parçasındaki veya vanadaki basınç kaybını karakterize etmek için kullanılan boyutsuz bir sayı olan K-değeri veya yerel kayıp katsayısı kavramını açıklar. ↩
-
Süreklilik denklemi ve Bernoulli prensibi ilkelerine dayanarak, bir akışkan bir kısıtlamadan (bir orifis) geçtiğinde meydana gelen basınç düşüşünün arkasındaki fiziği detaylandırır. ↩




