Як вібраційний резонанс впливає на продуктивність промислового обладнання?

Кошмар кожного інженера з технічного обслуговування - це несподівана поломка обладнання. Коли машини вібрують на своїй природній частоті, катастрофічні пошкодження можуть статися за лічені хвилини. Я бачив, як ця проблема коштувала компаніям тисячі простоїв.

Вібраційний резонанс¹ виникає, коли зовнішня сила збігається з власною частотою системи, спричиняючи посилені коливання, які можуть пошкодити обладнання. Розуміння та контроль цього явища має важливе значення для запобігання відмовам і продовження терміну служби обладнання.

Дозвольте поділитися короткою історією. Минулого року мені в паніці зателефонував клієнт з Німеччини. Його виробнича лінія зупинилася через те, що безштоковий циліндр сильно вібрував. А в чому проблема? Резонанс. Наприкінці цієї статті ви зрозумієте, як виявити та запобігти подібним проблемам у ваших системах.

Зміст

Формула власних частот: Як розрахувати вразливі місця вашої системи?
Модель "маса-пружина": Чому цей спрощений підхід такий цінний?
Оптимізація коефіцієнта демпфування: Які експерименти дають найкращі результати?
Висновок
Поширені запитання про вібраційний резонанс

Формула власних частот: Як розрахувати вразливі місця вашої системи?

Розуміння власної частоти вашого обладнання - це перший крок до запобігання виникненню резонансу. Це критичне значення визначає, коли ваша система найбільш вразлива до проблем з вібрацією.

У "The власна частота² (fn) системи можна обчислити за формулою: fn = (1/2π) × √(k/m), де k - коефіцієнт жорсткості, а m - маса. Цей розрахунок показує частоту, на якій ваша система буде резонувати, якщо її збудити відповідними зовнішніми силами.

Наочна навчальна діаграма, що пояснює власну частоту. На ілюстрації зображено просту систему маса-пружина, з блоком, позначеним як "Маса (m)", і пружиною, позначеною як "Жорсткість (k)". Лінії руху показують, що система коливається. Поруч з діаграмою чітко показано формулу "fn = (1/2π) × √(k/m)" зі стрілками, що явно пов'язують змінні "m" і "k" у рівнянні з відповідними фізичними величинами. — власна частота

Коли я відвідав виробничий завод у Швейцарії, я помітив, що їхні безштокові пневматичні циліндри передчасно виходять з ладу. Команда технічного обслуговування не розрахувала власну частоту їхньої установки. Застосувавши цю формулу, ми виявили, що їхня робоча швидкість була небезпечно близькою до власної частоти системи.

Практичне застосування розрахунків власної частоти

Формула власної частоти не просто теоретична - вона має пряме застосування в різних промислових умовах:

Вибір обладнання: Вибір компонентів з власними частотами, далекими від ваших умов експлуатації
Профілактичне обслуговування: Планування перевірок на основі профілів вібраційного ризику
Усунення несправностей: Визначення першопричини несподіваних вібрацій

Загальні значення власної частоти для промислових компонентів

Компонент	Типовий діапазон власних частот (Гц)
Безштокові циліндри	10-50 Гц
Монтажні кронштейни	20-100 Гц
Опорні конструкції	5-30 Гц
Регулююча арматура	40-200 Гц

Критичні фактори, що впливають на власну частоту

Розрахунок власної частоти здається простим, але кілька факторів можуть ускладнити реальне застосування:

Нерівномірний розподіл маси: Більшість промислових компонентів не мають ідеально розподіленої маси
Змінна жорсткість: Компоненти можуть мати різну жорсткість у різних напрямках
Точки підключення: Спосіб монтажу компонентів суттєво впливає на їхні вібраційні характеристики
Температурні ефекти: Як маса, так і властивості жорсткості можуть змінюватися з температурою

Модель "маса-пружина": Чому цей спрощений підхід такий цінний?

Модель маса-пружина забезпечує інтуїтивно зрозумілу основу для розуміння складних вібраційних систем. Вона зводить складні механізми до базових елементів, які інженери можуть легко аналізувати.

У "The масо-пружинна модель³ спрощує аналіз вібрацій, представляючи механічні системи як дискретні маси, з'єднані пружинами. Такий підхід дозволяє інженерам прогнозувати поведінку системи, виявляти потенційні резонансні проблеми та розробляти ефективні рішення без складної математики.

Порівняльна інфографіка, що пояснює модель "маса-пружина". Зліва, під написом "Складна механічна система", знаходиться детальна ілюстрація промислового двигуна. Велика стрілка з написом "Моделюється як" вказує вправо. Праворуч, під написом "Спрощена масо-пружинна модель", весь складний двигун представлений простим блоком з написом "Маса (m)", з'єднаним з простою пружиною з написом "Жорсткість (k)". — масо-пружинна модель

Я пам'ятаю, як працював з виробником автомобільних запчастин з Мічигану, який не міг зрозуміти, чому їхні керовані безштокові циліндри виходили з ладу. Змоделювавши їхню систему як просту систему з масою і пружиною, ми виявили, що кріпильні кронштейни діяли як ненавмисні пружини, створюючи резонансні умови.

Перетворення реальних систем у масопружні моделі

Застосувати цей підхід до вашого обладнання:

Визначте ключові маси: Визначте, які компоненти вносять значний внесок у вагу
Знайдіть пружинні елементи: Знайдіть компоненти, які накопичують і вивільняють енергію (власне пружини, гнучкі кріплення тощо).
Карта з'єднань: Задокументуйте, як взаємодіють маси та пружини
Спростити: Об'єднайте схожі елементи для створення керованої моделі

Типи масово-пружинних систем

Тип системи	Опис	Поширені програми
Одиночний DOF	Одна маса з однією пружиною	Прості пневматичні циліндри
Multi-DOF	Кілька мас з кількома пружинами	Складні машини з багатьма компонентами
Безперервний	Нескінченний DOF (вимагає іншого аналізу)	Балки, плити та оболонки

Розширені міркування щодо моделювання

Хоча базова модель "маса-пружина" є цінною, кілька удосконалень роблять її більш реалістичною:

Додавання демпферів: Реальні системи завжди мають розсіювання енергії
Врахування нелінійностей: Пружини не завжди слідують Закон Гука⁴ досконало
Облік вимушеної вібрації: Зовнішні сили змінюють поведінку системи
Включаючи ефекти зв'язку: Рух в одному напрямку може вплинути на інші напрямки

Оптимізація коефіцієнта демпфування: Які експерименти дають найкращі результати?

Демпфування - ваш найкращий захист від резонансних проблем. Пошук оптимального коефіцієнта демпфування шляхом експериментів може значно підвищити продуктивність і надійність системи.

Коефіцієнт демпфування⁵ Експерименти з оптимізації передбачають систематичне тестування різних конфігурацій демпфування, щоб знайти ідеальний баланс між контролем вібрації та чутливістю системи. Оптимальний коефіцієнт демпфування зазвичай знаходиться в межах від 0,2 до 0,7, забезпечуючи достатнє придушення вібрації без надмірних втрат енергії.

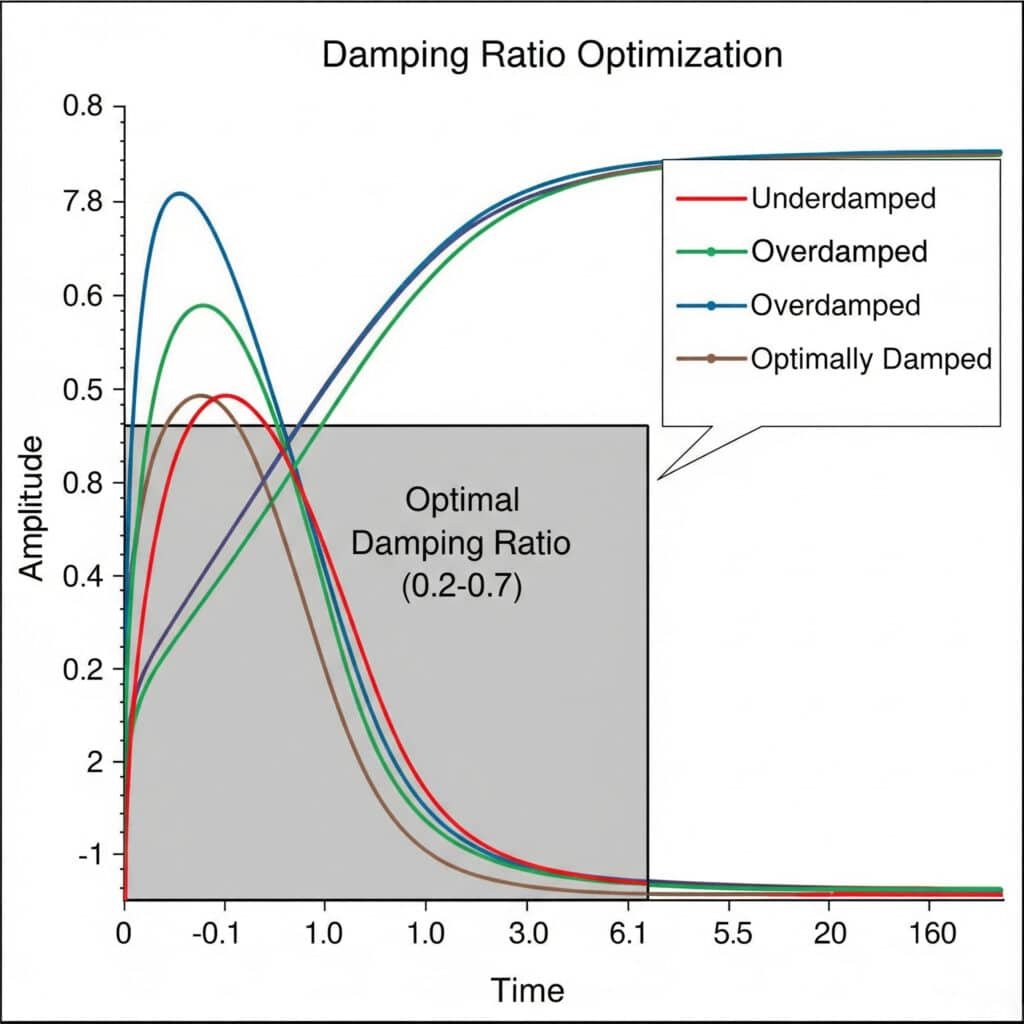
Графік, що ілюструє оптимізацію коефіцієнта демпфування шляхом побудови системи "Амплітуда" проти "Часу". Він відображає три різні криві відгуку: "Недодемпфована", яка значно коливається, "Передемпфована", яка повертається до нуля дуже повільно без коливань, і "Оптимально демпфована", яка швидко стабілізується з мінімальним перерегулюванням. Заштрихована область виділяє цей ідеальний відгук, позначений як "Оптимальний коефіцієнт демпфування (0,2-0,7)". — оптимізація коефіцієнта демпфування

Минулого місяця я допомагав французькому виробнику обладнання для харчової промисловості вирішити проблему постійної вібрації в їхніх магнітних безстрижневих циліндрах. Провівши серію експериментів з визначенням коефіцієнта демпфування, ми виявили, що оригінальна конструкція мала коефіцієнт демпфування лише 0,05 - занадто низький, щоб запобігти виникненню резонансних проблем.

Експериментальна установка для тестування коефіцієнта демпфування

Провести ефективні експерименти з оптимізації демпфування:

Базове вимірювання: Рекордний відгук системи без додаткового демпфування
Інкрементне тестування: Додавання демпферних елементів з контрольованим кроком
Вимірювання реакції: Вимірювання амплітуди, часу встановлення та частотної характеристики
Аналіз даних: Розрахувати коефіцієнт демпфування для кожної конфігурації
Валідація: Перевірте продуктивність в реальних умовах експлуатації

Порівняння технологій демпфування

Технологія демпфування	Переваги	Обмеження	Типові застосування
В'язкі демпфери	Передбачувана продуктивність, стабільна температура	Потребують технічного обслуговування, потенційні витоки	Важке машинобудування, прецизійне обладнання
Фрикційні демпфери	Проста конструкція, економічно ефективна	Знос з часом, нелінійна поведінка	Конструкційні опори, основні механізми
Демпфірування матеріалу	Без рухомих частин, компактний	Обмежений діапазон регулювання	Точні інструменти, віброізоляція
Активне демпфірування	Пристосованість до мінливих умов	Складний, вимагає потужності	Критичні застосування, обладнання зі змінною швидкістю

Оптимізація демпфування для різних умов експлуатації

Ідеальний коефіцієнт демпфування не є універсальним - він залежить від конкретного застосування:

Високошвидкісні операції: Нижчі коефіцієнти демпфування (0,1-0,3) підтримують чутливість
Прецизійне застосування: Більш високі коефіцієнти демпфування (0,5-0,7) забезпечують стабільність
Системи зі змінним навантаженням: Може знадобитися адаптивне демпфірування
Чутливі до температури середовища: Розглянемо демпфуючі матеріали зі стабільними властивостями

Практичний приклад: Оптимізація демпфування безштокового циліндра

Під час оптимізації безштокового циліндра подвійної дії для пакувальної машини ми протестували п'ять різних конфігурацій демпфірування:

Стандартні торцеві подушки: Коефіцієнт демпфування = 0.12
Подовжені подушки: Коефіцієнт демпфування = 0.25
Зовнішні амортизатори: Коефіцієнт демпфування = 0.41
Композитні монтажні кронштейни: Коефіцієнт демпфування = 0.38
Комбінований підхід (3+4): Коефіцієнт демпфування = 0.53

Комбінований підхід забезпечив найкращі показники, зменшивши амплітуду вібрації на 78% при збереженні прийнятного часу відгуку.

Висновок

Розуміння вібраційного резонансу за допомогою розрахунків власних частот, моделювання масової пружини та оптимізації коефіцієнта демпфування має вирішальне значення для запобігання виходу обладнання з ладу. Застосовуючи ці принципи, ви можете продовжити термін служби обладнання, зменшити час простою та підвищити загальну продуктивність системи.

Поширені запитання про вібраційний резонанс

Що таке вібраційний резонанс у промисловому обладнанні?

Вібраційний резонанс виникає, коли зовнішня сила збігається з власною частотою системи, викликаючи посилені коливання. У промисловому обладнанні це явище може призвести до надмірного руху, втоми компонентів і катастрофічних відмов, якщо ним не керувати належним чином.

Як я можу визначити, що моя система перебуває в резонансі?

Зверніть увагу на такі симптоми, як незрозуміле збільшення шуму, видима вібрація на певних швидкостях, передчасний вихід з ладу компонентів і погіршення продуктивності, що відбувається в постійних робочих точках. Інструменти для аналізу вібрації можуть підтвердити наявність резонансу.

У чому різниця між вимушеною вібрацією і резонансом?

Вимушені коливання виникають, коли на систему діє зовнішня сила, тоді як резонанс - це особливий стан, коли частота вимушених коливань збігається з власною частотою системи, що призводить до посилення відгуку. Будь-який резонанс включає в себе вимушені коливання, але не всі вимушені коливання викликають резонанс.

Як конструкція безштокового пневмоциліндра впливає на його вібраційні характеристики?

Конструкція безштокових пневматичних циліндрів з рухомою кареткою, внутрішньою системою ущільнень і напрямними механізмами створює унікальні проблеми з вібрацією. Подовжений профіль діє як балка, яка може згинатися, маса каретки створює інерційні сили, а ущільнювальні стрічки можуть створювати змінне тертя.

Які прості модифікації можуть зменшити резонанс в існуючому обладнанні?

Для існуючого обладнання, що має проблеми з резонансом, розгляньте можливість додавання маси для зміни власної частоти, встановлення зовнішніх демпферів або амортизаторів, модифікації методів монтажу, включаючи віброізоляцію, або регулювання робочих швидкостей, щоб уникнути резонансних частот.

Надає фундаментальне пояснення механічного резонансу, часто з наочними прикладами, демонструючи, як невелика періодична сила може викликати коливання великої амплітуди в системі. ↩
Пропонує детальний погляд на фізику власної частоти, специфічної частоти, на якій система має тенденцію коливатися за відсутності будь-якої рушійної або демпфуючої сили. ↩
Пояснює принципи моделі "маса-пружина" - фундаментальної ідеалізації у фізиці та інженерії, яка використовується для аналізу складних систем, що демонструють простий гармонійний рух. ↩
Детальніше Закон Гука - принцип фізики, який стверджує, що сила, необхідна для розтягування або стиснення пружини на певну відстань, прямо пропорційна цій відстані. ↩
Описує коефіцієнт демпфування, безрозмірну міру, яка визначає, як коливання в системі затухають після збурення, що є критично важливим для контролю резонансу. ↩

Привіт, я Чак, старший експерт з 15-річним досвідом роботи в галузі пневматики. У Bepto Pneumatic я зосереджуюсь на наданні високоякісних, індивідуальних пневматичних рішень для наших клієнтів. Мій досвід охоплює промислову автоматизацію, проектування та інтеграцію пневматичних систем, а також застосування та оптимізацію ключових компонентів. Якщо у вас виникли питання або ви хочете обговорити потреби вашого проекту, будь ласка, зв'яжіться зі мною за адресою chuck@bepto.com.