Як насправді опір потоку впливає на продуктивність пневматичної системи?

Технічна інфографіка, що пояснює опір потоку в пневматичних системах. На ній зображено схему труби з прямою ділянкою, за якою йде вигин. Графік, побудований над трубою, показує рівень тиску. На прямій ділянці тиск плавно знижується, що позначено як "Втрати на тертя". На вигині тиск різко падає східчасто, позначений як "Місцеві втрати". Ілюстрація чітко розрізняє два типи опору та їхній сукупний вплив на тиск. — Опір насправді впливає

Ви боретеся з повільною швидкістю циліндрів, непослідовним рухом або недостатнім зусиллям у ваших пневматичних системах? Ці поширені проблеми часто виникають через неправильно зрозумілого винуватця: опір потоку. Багато інженерів визначають розміри пневматичних компонентів, виходячи виключно з вимог до тиску та зусилля, нехтуючи критичним впливом опору потоку на реальну продуктивність.

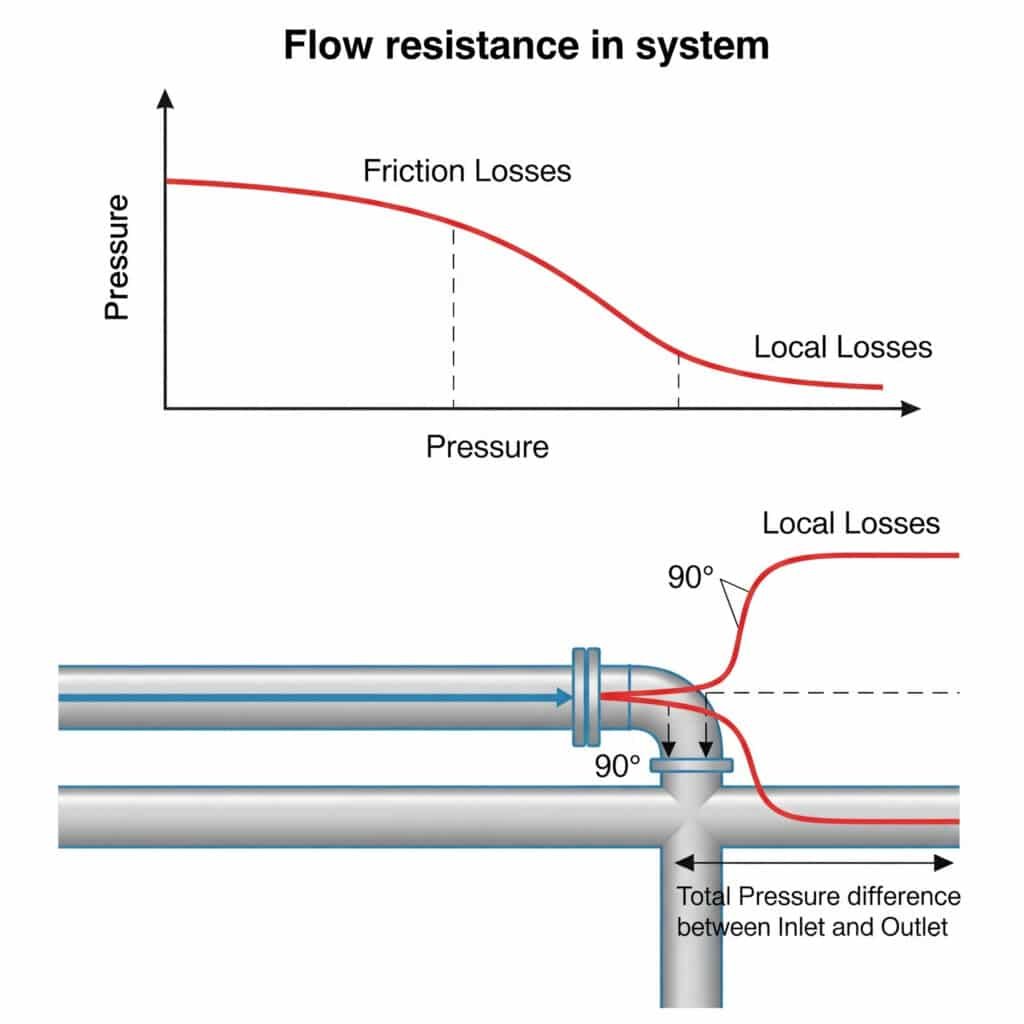
Опір потоку в пневматичних системах створює перепади тиску, які зменшують доступну силу, обмежують максимальну швидкість і спричиняють нерівномірний рух. Цей опір виникає як через тертя вздовж прямих труб (втрати на тертя), так і через перебої в роботі фітингів, вигинів і клапанів (місцеві втрати). Разом ці опори можуть знизити фактичну продуктивність системи на 20-50% порівняно з теоретичними розрахунками.

За понад 15 років роботи в компанії Bepto з пневматичними системами я бачив незліченну кількість випадків, коли розуміння та усунення опору потоку перетворило малоефективні системи на надійні та ефективні. Дозвольте мені поділитися тим, що я дізнався про розрахунок і мінімізацію цих прихованих вбивць продуктивності.

Зміст

Як ви насправді розраховуєте втрати на тертя в пневматичних лініях?
Чому метод еквівалентної довжини має вирішальне значення для точного проектування систем?
Що відбувається, коли повітря проходить через зменшені перерізи отворів?
Висновок
Поширені запитання про опір потоку в пневматичних системах

Як ви насправді розраховуєте втрати на тертя в пневматичних лініях?

Втрати на тертя в прямих трубах і трубах є основою розрахунків опору потоку, але багато інженерів покладаються на спрощені емпіричні правила, які призводять до створення систем менших розмірів.

Втрати на тертя в пневматичних лініях розраховуються за формулою Рівняння Дарсі-Вейсбаха¹ΔP = λ(L/D)(ρv²/2), де λ - коефіцієнт тертя, L - довжина труби, D - діаметр труби, ρ - густина повітря, v - швидкість потоку. Для пневматичних систем коефіцієнт тертя λ залежить від Число Рейнольдса² і відносної шорсткості, і зазвичай визначається за допомогою таблиць пошуку або Діаграма Муді³.

Розуміння втрат на тертя має практичне значення для проектування системи та усунення несправностей. Дозвольте мені розбити це на практичні ідеї.

Ефективне використання таблиць коефіцієнтів тертя

Коефіцієнт тертя (λ) є ключовим параметром при розрахунку перепадів тиску, але визначення його значення вимагає врахування умов потоку:

Режим течії	Число Рейнольдса (Re)	Визначення коефіцієнта тертя
Ламінарний потік	Re < 2000	λ = 64/Re
Перехідний потік	2000 < Re < 4000	Ненадійний - уникайте проектування в цьому діапазоні
Турбулентний потік	Re > 4000	Використовуйте таблиці пошуку на основі відносної шорсткості (ε/D)

Практична таблиця пошуку коефіцієнтів тертя

Для турбулентного потоку в пневматичних системах використовуйте цю спрощену таблицю:

Матеріал труби	Відносна шорсткість (ε/D)	Коефіцієнт тертя (λ) при звичайних числах Рейнольдса
		Re = 10 000
Гладкі трубки (ПВХ, поліуретан)	0.0001 – 0.0005	0.031
Алюмінієва труба	0.001 – 0.002	0.035
Оцинкована сталь	0.003 – 0.005	0.042
Іржава сталь	0.01 – 0.05	0.054

Розрахунок перепаду тиску в реальних пневматичних системах

Давайте розглянемо практичний приклад:

Параметр	Значення/розрахунок	Приклад
Діаметр труби (D)	Внутрішній діаметр	8 мм (0,008 м)
Довжина труби (L)	Загальна пряма довжина	5m
Витрата (Q)	З системних вимог	20 стандартних літрів/секунду
Щільність повітря (ρ)	При робочому тиску	7,2 кг/м³ при 6 бар
Швидкість потоку (v)	v = Q/(π×D²/4)	v = 0,02 м³/с/(π×0,008²/4) = 398 м/с
Число Рейнольдса (Re)	Re = ρvD/μ	Re = 7,2×398×0,008/1,8×10-⁵ = 1 273 600
Відносна шорсткість	Для поліуретанових труб	0.0003
Коефіцієнт тертя (λ)	З таблиці пошуку	0.017
Перепад тиску (ΔP)	ΔP = λ(L/D)(ρv²/2)	ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 бар

Реальне застосування: Вирішення проблем зі швидкістю обертання циліндрів

Минулого року я працював з Сарою, інженером-технологом компанії з виробництва пакувального обладнання у Вісконсині. Її безштокова циліндрова система працювала зі швидкістю лише 60% від очікуваної, незважаючи на правильно підібраний розмір циліндра і достатній тиск подачі.

Проаналізувавши її систему, я виявив, що вона використовувала 6-міліметрову трубку для високопродуктивного застосування. Втрати на тертя спричиняли падіння тиску на 2,1 бар, що значно знижувало доступну силу та швидкість. Перейшовши на 10-міліметрові трубки, ми зменшили втрати тиску до 0,4 бар, і її система одразу ж досягла необхідної продуктивності без будь-яких інших змін.

Фактори, що впливають на втрати на тертя в реальних системах

На фактичні втрати на тертя впливають кілька факторів:

Температура повітря: Вищі температури збільшують в'язкість і тертя
Забруднення: Бруд і масло можуть збільшити ефективну шорсткість
Згинання труб: Мікродеформація у зігнутих трубах збільшує опір
Вікове погіршення: Корозія та відкладення з часом збільшують шорсткість
Робочий тиск: Вищий тиск збільшує щільність і втрати

Чому метод еквівалентної довжини має вирішальне значення для точного проектування систем?

Місцеві втрати на фітингах, клапанах і вигинах часто перевищують втрати на тертя в прямих трубах, але багато інженерів або ігнорують їх, або використовують грубі методи оцінки, які призводять до проблем з продуктивністю.

Метод еквівалентної довжини перетворює місцеві втрати від фітингів та клапанів в еквівалентну довжину прямої труби, яка спричинить таке ж падіння тиску. Це розраховується за формулою Le = K(D/λ), де Le - еквівалентна довжина, K - коефіцієнт коефіцієнт локальних втрат⁴де D - діаметр труби, а λ - коефіцієнт тертя. Цей метод спрощує розрахунки і дає більш точні прогнози продуктивності системи.

Давайте розглянемо, як ефективно застосовувати цей метод у проектуванні пневматичних систем.

Таблиці еквівалентної довжини для поширених пневматичних компонентів

Ось практична довідкова таблиця для поширених пневматичних компонентів:

Компонент	K-значення	Еквівалентна довжина (Le/D)
90° Лікоть (гострий)	0.9	30
90° Коліно (стандартний радіус)	0.3	10
45° Лікоть	0.2	7
Т-подібний перехід (наскрізний потік)	0.3	10
Т-подібний перехід (розгалуження)	1.0	33
Кульовий кран (повністю відкритий)	0.1	3
Засувка (повністю відкрита)	0.2	7
Швидкоз'ємне з'єднання	0.4-0.8	13-27
Зворотний клапан	1.5-2.5	50-83
Стандартний клапан регулювання витрати	1.0-3.0	33-100

Застосування методу еквівалентної довжини

Ефективно використовувати цей метод:

Визначте всі компоненти пневматичного контуру
Знайдіть K-значення або еквівалентне відношення довжини (Le/D) для кожного компонента
Розрахуйте еквівалентну довжину, помноживши на діаметр труби
Додайте всі еквівалентні довжини до фактичної довжини прямої труби
Використовуйте загальну ефективну довжину в розрахунках втрат на тертя

Наприклад, система з 5 м прямої 8-міліметрової труби плюс чотири коліна 90°, одне Т-подібне з'єднання і два швидкороз'ємних з'єднання:

Компонент	Кількість	Le/D	Еквівалентна довжина
Лікті 90° Коліна	4	10	4 × 10 × 0,008 м = 0,32 м
Т-подібне перехрестя	1	10	1 × 10 × 0,008 м = 0,08 м
Швидкі з'єднання	2	20	2 × 20 × 0,008 м = 0,32 м
Загальна еквівалентна довжина			0.72m
Фактична пряма довжина			5.00m
Загальна ефективна довжина			5.72m

Це означає, що ваша 5-метрова система насправді поводиться як 5,72-метрова через місцеві втрати - збільшення ефективної довжини на 14,4%.

Практичний приклад: Оптимізація розміщення клапанів у складальних системах

Нещодавно я допомагав Мігелю, інженеру з автоматизації на заводі зі складання електроніки в Арізоні. Його маніпулятор мав непослідовний рух і коливання тривалості циклу, незважаючи на використання високоякісних компонентів.

Аналіз показав, що його клапанний колектор був розташований на відстані 3 м від циліндрів, а контур включав численні фітинги. Розрахунок еквівалентної довжини показав, що фактична відстань у 3 м мала ефективну довжину 7,2 м через місцеві втрати - більш ніж удвічі більше, ніж відстань по прямій трубі!

Перемістивши клапанний колектор ближче до циліндрів і усунувши кілька фітингів, ми зменшили ефективну довжину з 7,2 м до 2,1 м. Це зменшило перепад тиску на 70%, що призвело до стабільного руху та скорочення часу циклу на 15%.

Практичні поради щодо мінімізації локальних втрат

Для зменшення локальних втрат у ваших пневматичних системах:

Використовуйте загнуті або закруглені лікті замість різких вигинів (зменшує значення K на 67%)
Мінімізуйте кількість фітингів шляхом планування більш прямих маршрутів
Вибирайте компоненти з низьким рівнем обмежень як повнопрохідні кульові крани, де це доречно
Правильно підбирайте розмір фурнітури - недостатньо велика фурнітура призводить до непропорційних втрат
Розміщуйте клапани поруч із приводами для мінімізації ефективної довжини НКТ

Що відбувається, коли повітря проходить через зменшені перерізи отворів?

Зменшені прохідні перетини в пневматичних контурах - наприклад, частково закриті клапани, фітинги меншого розміру або переходи діаметрів - створюють значні обмеження потоку, які можуть серйозно вплинути на продуктивність системи.

Коли повітря проходить через зменшені перерізи отворів, перепади тиску⁵ відбуваються за формулою ΔP = ρ(v₂² - v₁²)/2, де v₁ - швидкість перед звуженням, а v₂ - швидкість в звуженні. Це можна компенсувати за допомогою коефіцієнта компенсації співвідношення діаметрів C = (1 - (d/D)⁴), де d - зменшений діаметр, а D - початковий діаметр. Цей коефіцієнт допомагає спрогнозувати фактичну продуктивність системи та уникнути використання компонентів меншого розміру.

Давайте розглянемо практичне значення зменшених перерізів отворів і те, як їх враховувати при проектуванні системи.

Розрахунок перепадів тиску на діаметральних переходах

Коли повітря перетікає з більшого діаметра в менший, перепад тиску можна розрахувати за допомогою:

Параметр	Формула	Приклад
Початковий діаметр (D)	Зі специфікацій	10 мм
Зменшений діаметр (d)	Зі специфікацій	6 мм
Співвідношення отворів (d/D)	Просте ділення	0.6
Витрата (Q)	З системних вимог	15 стандартних літрів/секунду
Швидкість у вихідній трубі (v₁)	v₁ = Q/(π×D²/4)	191 м/с
Швидкість у приведеному перерізі (v₂)	v₂ = Q/(π×d²/4)	531 м/с
Перепад тиску (ΔP)	ΔP = ρ(v₂² - v₁²)/2	0,88 бар
Компенсаційний коефіцієнт (C)	C = (1 - (d/D)⁴)	0.87

Поширені сценарії скорочення свердловин та їх вплив

Ось як різні варіанти зменшення отворів впливають на пропускну здатність:

Зменшення отворів	Зменшення пропускної здатності	Збільшення перепаду тиску
10 мм до 8 мм	36%	2.4×
10 мм до 6 мм	64%	7.7×
10 мм до 4 мм	84%	39×
8 мм до 6 мм	44%	3.2×
8 мм до 4 мм	75%	16×
6 мм до 4 мм	56%	5.1×

Ці цифри показують, чому, здавалося б, незначне зменшення діаметру може мати драматичний вплив на продуктивність системи.

Кумулятивний ефект численних обмежень

У реальних пневматичних контурах послідовно зустрічаються декілька обмежень. Їхній вплив є кумулятивним і може бути розрахований за допомогою:

Перетворіть кожне обмеження в еквівалентний йому С-фактор
Розрахуйте загальний С-фактор: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
Використовуйте цей сумарний коефіцієнт для визначення загального зниження продуктивності системи

Практичний приклад: Вирішення проблем невідповідності між клапаном і приводом

Минулого місяця я працював з Томасом, керівником технічного обслуговування на меблевій фабриці в Північній Кароліні. Його нова безштокова система циліндрів працювала менш ніж на половину очікуваної швидкості, незважаючи на використання рекомендованого виробником розміру клапана.

Дослідження виявило численні зменшення отворів у його контурі:

10-міліметрова лінія подачі до 8-міліметрових портів клапанів (C₁ = 0,36)
8-міліметрові отвори клапанів до 6-міліметрових фітингів (C₂ = 0,44)
6 мм фітинги до 8 мм портів балонів з внутрішніми обмеженнями (C₃ = 0,32)

Загальний коефіцієнт компенсації склав Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, тобто його система втрачала 75% своєї теоретичної пропускної здатності!

Замінивши всі компоненти системи на компоненти належного розміру, ми усунули ці обмеження і досягли необхідної продуктивності без зміни циліндра або тиску подачі.

Практичні стратегії мінімізації втрат при скороченні свердловин

Зменшити втрати від скорочення отворів:

Послідовний розмір компонентів по всьому пневматичному контуру
Використовуйте найбільший практичний розмір трубки для високопродуктивних застосувань
Зверніть увагу на внутрішні обмеження компонентіва не тільки розміри з'єднань
Розглянемо паралельні шляхи потоку для високих вимог до потоку
Усуньте непотрібні адаптери та переходи де це можливо

Принцип "найслабшої ланки" в пневматичних системах

Пам'ятайте, що продуктивність вашої пневматичної системи обмежується її найважчим компонентом. Один елемент меншого розміру може звести нанівець переваги правильно підібраних компонентів в інших частинах системи.

Наприклад, система з 10-міліметровими трубками, 10-міліметровими клапанами, але 6-міліметровими фітингами на балоні буде працювати практично так само, як і система з 6-міліметровими компонентами, але коштуватиме дорожче.

Висновок

Розуміння і правильний розрахунок опору потоку за допомогою таблиць коефіцієнтів тертя, методів еквівалентної довжини і компенсації зменшеного отвору є важливим для проектування пневматичних систем, які будуть працювати відповідно до очікувань в реальних умовах. Застосовуючи ці методи розрахунку і принципи проектування, ви можете оптимізувати свої безштокові циліндри та інші пневматичні системи для досягнення максимальної продуктивності і надійності.

Поширені запитання про опір потоку в пневматичних системах

Який перепад тиску допустимий у пневматичній системі?

Допустимий перепад тиску залежить від вимог вашого застосування, але, як правило, для ефективної роботи слід обмежити загальний перепад тиску до 10-15% тиску подачі. Для системи з тиском 6 бар це означає, що загальний перепад тиску не повинен перевищувати 0,6-0,9 бар. У критично важливих системах для підтримки стабільної роботи можуть знадобитися ще менші перепади тиску - 5-8%.

Який зв'язок між діаметром трубки і перепадом тиску?

Падіння тиску обернено пропорційне п'ятому степеню діаметра (D⁵) для турбулентного потоку в пневматичних системах. Це означає, що подвоєння діаметра трубки зменшує перепад тиску приблизно в 32 рази. Наприклад, збільшення діаметру трубки з 6 мм до 12 мм може зменшити перепад тиску з 1,5 бар до 0,047 бар за тих самих умов потоку.

Як визначити правильний розмір трубки для мого пневматичного застосування?

Виберіть розмір трубки, виходячи з вимог до швидкості потоку і допустимого перепаду тиску. Розрахуйте число Рейнольдса і коефіцієнт тертя, а потім використовуйте рівняння Дарсі-Вейсбаха для визначення втрат тиску для різних діаметрів. Виберіть найменший діаметр, який утримує втрати тиску в прийнятних межах (зазвичай <10% тиску подачі), враховуючи при цьому обмеження простору і вартість.

Що створює більше обмежень: коліно 90° чи 5 метрів прямої труби?

Гостре коліно 90° зазвичай створює опір, еквівалентний 30 діаметрам прямої труби. Для 8-міліметрових труб одне гостре коліно дорівнює приблизно 240 мм (30 × 8 мм) прямої труби. Це означає, що 5 метрів прямої труби створюють приблизно в 21 раз більший опір, ніж одне коліно. Однак системи часто містять кілька колін і фітингів, сумарний ефект яких може перевищувати втрати на прямій ділянці.

Як швидкоз'ємні фітинги впливають на продуктивність системи?

Стандартні швидкоз'ємні фітинги зазвичай спричиняють місцеві втрати, еквівалентні 15-25 діаметрам прямої труби. Більш того, багато швидкороз'ємних з'єднань мають внутрішні обмеження, менші за номінальний розмір. Наприклад, 10-міліметрове швидкороз'ємне з'єднання може мати внутрішнє обмеження лише 7-8 мм, що призводить до зменшення прохідного перерізу, яке може знизити пропускну здатність на 50-70% в цій точці.

Як частково закриті клапани регулювання потоку впливають на продуктивність системи?

Регулятор потоку, закритий на 50% повного прохідного перерізу, зменшує потік не лише на 50% - він зменшує потік приблизно на 75% через нелінійну залежність між діаметром і пропускною здатністю. Падіння тиску збільшується відповідно до квадрату зміни швидкості, тому зменшення ефективного діаметру вдвічі збільшує падіння тиску приблизно в 16 разів за тих самих умов потоку.

Надає детальний аналіз рівняння Дарсі-Вейсбаха, фундаментальної і широко використовуваної формули в гідродинаміці для розрахунку втрат тиску через тертя в трубі. ↩
Пропонує чітке визначення числа Рейнольдса, критичної безрозмірної величини, яка використовується для прогнозування структури потоку (ламінарного або турбулентного) в різних ситуаціях течії рідини. ↩
Представлено діаграму Муді - комплексний графік, який відображає залежність коефіцієнта тертя Дарсі від числа Рейнольдса та відносної шорсткості, що є стандартним інструментом для інженерів для визначення перепаду тиску в трубах. ↩
Пояснює концепцію K-значення, або коефіцієнта місцевих втрат, безрозмірного числа, що використовується для характеристики втрат тиску в трубопровідній арматурі або клапані в рамках методу еквівалентної довжини. ↩
Детально описує фізику перепаду тиску, що виникає при проходженні рідини через обмеження (отвір), на основі принципів рівняння нерозривності та принципу Бернуллі. ↩

Привіт, я Чак, старший експерт з 15-річним досвідом роботи в галузі пневматики. У Bepto Pneumatic я зосереджуюсь на наданні високоякісних, індивідуальних пневматичних рішень для наших клієнтів. Мій досвід охоплює промислову автоматизацію, проектування та інтеграцію пневматичних систем, а також застосування та оптимізацію ключових компонентів. Якщо у вас виникли питання або ви хочете обговорити потреби вашого проекту, будь ласка, зв'яжіться зі мною за адресою chuck@bepto.com.