A gyártási leállások évente milliókba kerülnek a vállalatoknak. Az ipari automatizálási rendszerek 80% pneumatikus hengerek hajtják. Sok mérnök mégsem érti teljesen a mögöttes fizikát, amely ezeket a rendszereket olyan megbízhatóvá és hatékonnyá teszi.
A pneumatikus hengerek elmélete a Pascal-törvényen alapul, ahol a sűrített levegő nyomása egy zárt kamrában minden irányban egyformán hat, és a nyomáskülönbségek révén a pneumatikus energiát mechanikus lineáris vagy forgó mozgássá alakítja.
Két évvel ezelőtt egy James Thompson nevű manchesteri brit mérnökkel dolgoztam együtt, akinek a gyártósorai folyamatosan meghibásodtak. A csapata nem értette, hogy a pneumatikus rendszerük miért vesztette el időnként az energiát. Miután elmagyaráztuk az alapvető elméletet, azonosítottuk a nyomáseséssel kapcsolatos problémákat, amivel a vállalat 200 000 font termelési veszteséget takarított meg.
Tartalomjegyzék
- Mi a pneumatikus hengerek alapvető fizikája?
- Hogyan hoz létre a nyomáskülönbség mozgást a pneumatikus rendszerekben?
- Melyek azok a kulcsfontosságú összetevők, amelyek a pneumatikus elméletet működtetik?
- Hogyan alkalmazzák ezeket az elveket a különböző pneumatikus henger típusok?
- Milyen tényezők befolyásolják a pneumatikus hengerek teljesítményét?
- Hogyan hasonlítható össze a pneumatikus elmélet a hidraulikus és az elektromos rendszerekkel?
- Következtetés
- GYIK a pneumatikus henger elméletéről
Mi a pneumatikus hengerek alapvető fizikája?
A pneumatikus hengerek alapvető fizikai elvek alapján működnek, amelyek több mint egy évszázada az ipari automatizálást hajtják. Ezen alapok megértése segít a mérnököknek jobb rendszerek tervezésében és a problémák hatékony elhárításában.
A pneumatikus hengerek a Pascal-törvény, a Boyle-törvény és a Newton mozgástörvényei1, a sűrített levegő energiáját mechanikai erővé alakítja a dugattyúfelületek közötti nyomáskülönbségek révén.
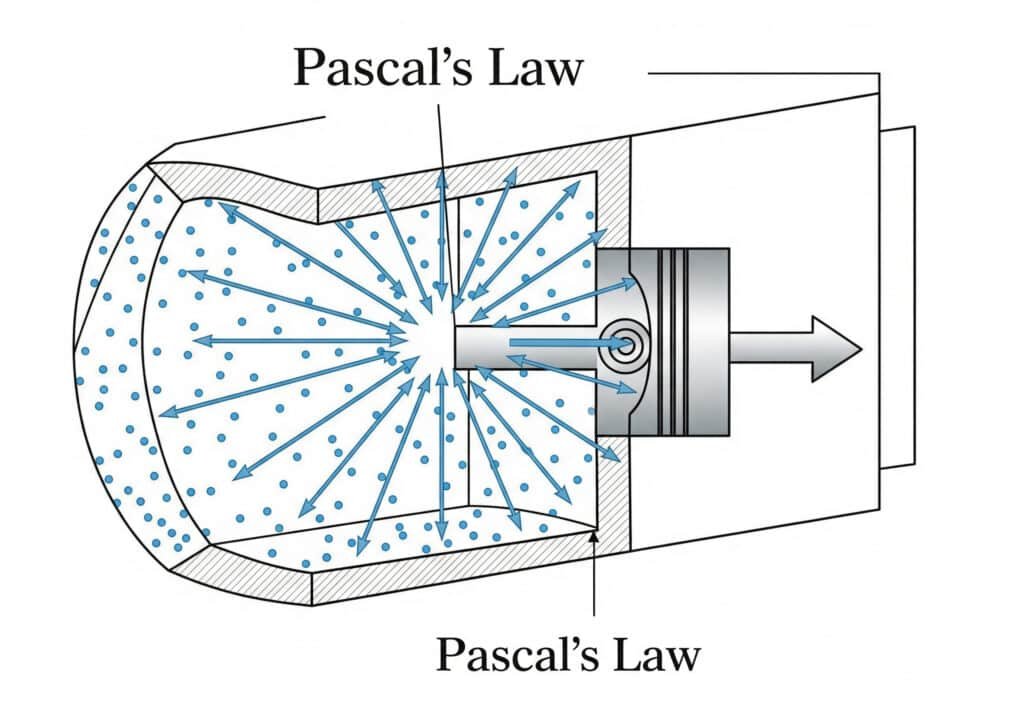
Pascal törvényének alkalmazása
Pascal törvénye kimondja, hogy egy zárt folyadékra kifejtett nyomás minden irányban egyformán terjed. A pneumatikus hengereknél ez azt jelenti, hogy a sűrített levegő nyomása egyenletesen hat a dugattyú teljes felületén.
Az alapvető erőegyenlet a következő: Erő = nyomás × terület
Egy 4 hüvelyk átmérőjű henger esetében 100 PSI nyomáson:
- Dugattyú területe = π × (2)² = 12,57 négyzetcentiméter
- Kimenő erő = 100 PSI × 12,57 = 1,257 font
Boyle törvénye és a levegő tömörítése
Boyle törvénye megmagyarázza, hogyan változik a levegő térfogata állandó hőmérsékleten a nyomás függvényében. Ez az elv szabályozza, hogy a sűrített levegő hogyan tárolja az energiát, és hogyan adja le azt a henger működése során.
Amikor a levegő a légköri nyomásról (14,7 PSI) 114,7 PSI-re (abszolút nyomás) sűrűsödik, a térfogata körülbelül 87%-tel csökken. Ez a sűrített levegő potenciális energiát tárol, amely a henger kitágítása során mozgási energiává alakul át.
Newton törvényei a pneumatikus mozgásban
Newton második törvénye (F = ma) határozza meg a henger gyorsulását és sebességét. A nagyobb nyomáskülönbség nagyobb erőket hoz létre, ami gyorsabb gyorsulást eredményez, amíg a súrlódás és a terhelés ellenállása ki nem egyenlíti a hajtóerőt.
Fizikai kulcskapcsolatok:
| Törvény | Alkalmazás | Formula | A teljesítményre gyakorolt hatás |
|---|---|---|---|
| Pascal törvénye | Erőfejlesztés | F = P × A | Meghatározza a maximális erőt |
| Boyle törvénye | Légsűrítés | P₁V₁ = P₂V₂ | Befolyásolja az energiatárolást |
| Newton 2. | Mozgásdinamika | F = ma | Szabályozza a sebességet/gyorsítást |
| Az energia megőrzése | Hatékonyság | Ein = Eout + veszteségek | Meghatározza a rendszer hatékonyságát |
Hogyan hoz létre a nyomáskülönbség mozgást a pneumatikus rendszerekben?
A nyomáskülönbség a hajtóerő minden pneumatikus henger mozgása mögött. Minél nagyobb a nyomáskülönbség a dugattyún, annál nagyobb erőt és sebességet generál a henger.
A mozgás akkor jön létre, amikor sűrített levegő kerül az egyik henger kamrába, míg a másik kamra a légkörbe, és ez nyomáskülönbséget hoz létre, amely a dugattyú mozgását a hengerfurat mentén hajtja végre.
Egyszeres működésű henger elmélete
Az egyszeresen működő hengerek csak egy irányban használják a sűrített levegőt. A rugó vagy a gravitáció visszahúzza a dugattyút az eredeti helyzetébe, amikor a légnyomás megszűnik.
Az effektív erő számításánál figyelembe kell venni a rugóellenállást:
Nettó erő = (nyomás × terület) - rugóerő - súrlódás
A rugóerő jellemzően a maximális hengererő 10-30% között mozog, csökkentve a teljes teljesítményt, de biztosítva a megbízható visszatérő mozgást.
Dupla működésű henger elmélete
A kettős működésű hengerek sűrített levegőt használnak mind a kitoláshoz, mind a behúzáshoz. Ez a kialakítás mindkét irányban maximális erőt és a dugattyú helyzetének pontos szabályozását biztosítja.
Erőszámítások kettős működésű hengerekhez:
Hosszabbító erő: F = P × (teljes dugattyúterület)
Visszahúzó erő: F = P × (teljes dugattyúfelület - rúdfelület)
A rúd területének csökkentése azt jelenti, hogy a behúzóerő mindig kisebb, mint a kinyújtóerő. Egy 4 hüvelykes henger esetében 1 hüvelykes rúddal:
- Bővítési terület: 12,57 négyzetcentiméter
- Visszahúzódó terület: 12,57 - 0,785 = 11,785 négyzet hüvelyk
- Erőkülönbség: kb. 6% kevesebb behúzáskor
A nyomásesés elmélete
Nyomáscsökkenés2 a pneumatikus rendszerekben a súrlódás, a szerelvények és a szelepek korlátozása miatt. Ezek a veszteségek közvetlenül csökkentik a henger teljesítményét, és a rendszer tervezésekor figyelembe kell venni őket.
Gyakori nyomásesés forrásai:
- Légvezetékek: 1-3 PSI 100 lábonként
- Szerelvények: PSI: 0,5-2 PSI egyenként
- Szelepek: 2-8 PSI a kialakítástól függően
- Szűrők: 1-5 PSI, ha tiszta
Melyek azok a kulcsfontosságú összetevők, amelyek a pneumatikus elméletet működtetik?
A pneumatikus hengerek elmélete a pontosan megtervezett alkatrészek együttműködésén alapul. Minden egyes alkatrész meghatározott funkciót tölt be a sűrített levegő energiájának mechanikai mozgássá alakításában.
Az alapvető alkotóelemek közé tartozik a hengercső, a dugattyúegység, a rúd, a tömítések és a zárókupakok, amelyek mindegyikét úgy tervezték, hogy a nyomást visszatartsák, a mozgást vezessék és az erőt hatékonyan átadják.
Hengercső mérnöki tervezés
A hengercsőnek ellen kell állnia a belső nyomásnak, miközben a furat pontos méreteit megtartja. A legtöbb ipari palack varrat nélküli acél- vagy alumíniumcsövet használ, amelynek csiszolt belső felületek3.
Hordó specifikációk:
| Anyag | Nyomásértékelés | Felületkezelés | Tipikus alkalmazások |
|---|---|---|---|
| Alumínium | 250 PSI-ig | 16-32 Ra | Könnyű teherbírású, élelmiszeripari minőségű |
| Acél | 500 PSI-ig | 8-16 Ra | Nagy teherbírású, nagynyomású |
| Rozsdamentes acél | Akár 300 PSI | 8-32 Ra | Korrozív környezetek |
Dugattyú tervezési elmélet
A dugattyúk a két légkamra lezárása közben a rúdra kifejtett nyomóerőt továbbítják. A dugattyú kialakítása befolyásolja a henger hatékonyságát, sebességét és élettartamát.
A modern dugattyúk több tömítőelemet használnak:
- Elsődleges tömítés: Megakadályozza a kamrák közötti légszivárgást
- Gyűrűk viselése: Vezeti a dugattyú mozgását és megakadályozza a fém érintkezését
- Másodlagos tömítések: Biztonsági tömítés kritikus alkalmazásokhoz
Tömítési rendszer elmélete
A tömítések kritikus fontosságúak a nyomáskülönbségek fenntartásában. A tömítés meghibásodása a pneumatikus hengerek problémáinak leggyakoribb oka az ipari alkalmazásokban.
Pecsét teljesítménytényezők:
- Anyag kiválasztása: Ellen kell állnia a levegő áteresztésének és a kopásnak
- Groove Design: A megfelelő méretek megakadályozzák a tömítés extrudálását
- Felületkezelés: A sima felületek csökkentik a tömítés kopását
- Üzemi nyomás: A nagyobb nyomás speciális tömítéseket igényel
Hogyan alkalmazzák ezeket az elveket a különböző pneumatikus henger típusok?
A különböző pneumatikus hengerek kialakítása ugyanazt az alapelméletet alkalmazza, de a teljesítményt az egyes alkalmazásokhoz optimalizálják. Ezeknek a változatoknak a megértése segít a mérnököknek a megfelelő megoldások kiválasztásában.
A különböző hengertípusok az alapvető pneumatikai elméletet olyan speciális kialakításokkal módosítják, mint a rúd nélküli hengerek, a forgó működtetők és a többállású hengerek, amelyek mindegyike optimalizálja az erő, a sebesség vagy a mozgás jellemzőit.
Rúd nélküli pneumatikus henger
Rúd nélküli hengerek4 Elmélet
a hagyományos dugattyúrudat kiküszöbölése, ami hosszabb löketeket tesz lehetővé kompakt helyeken. Mágneses tengelykapcsolót vagy kábelrendszert használnak a hengeren kívüli mozgás átvitelére.
Mágneses tengelykapcsoló kialakítása:
A belső dugattyú állandó mágneseket tartalmaz, amelyek a henger falán keresztül egy külső kocsival kapcsolódnak össze. Ez a kialakítás megakadályozza a légszivárgást, miközben a dugattyú teljes erejét átadja.
Erőátvitel hatékonysága: 95-98% megfelelő mágneses csatolással
Maximális löket: Csak a henger hossza korlátozza, akár több mint 20 lábig.
Sebesség Képesség: Akár 60 hüvelyk másodpercenként, a terheléstől függően
Forgószelep elmélet
Forgó pneumatikus működtetők5 a lineáris dugattyúmozgást fogaskerék-mechanizmusok vagy lapátkialakítások révén forgó mozgássá alakítják át. Ezek a rendszerek pneumatikus elméletet alkalmaznak a pontos szögpozicionálás létrehozásához.
Vane-típusú forgó működtetők:
A sűrített levegő egy hengeres kamrában lévő lapátra hat, és forgatónyomatékot hoz létre. A nyomaték kiszámítása a következő: Nyomaték = Nyomás × szárnyfelület × sugár
Többállású henger elmélete
A többállású hengerek több légkamrát használnak a köztes megállási pozíciók létrehozásához. Ez a kialakítás a pneumatikus elméletet alkalmazza összetett szeleprendszerekkel a pontos pozícionálás vezérléséhez.
Gyakori konfigurációk:
- Háromállású: Két közbenső megálló és teljes kihúzás
- Ötállású: Négy közbenső megállás és teljes löket
- Változó pozíció: Végtelen pozícionálás szervószelep vezérléssel
Milyen tényezők befolyásolják a pneumatikus hengerek teljesítményét?
Több tényező befolyásolja, hogy a pneumatikus elmélet mennyire válik átültethetővé a valóságban. Ezeknek a változóknak a megértése segít a mérnököknek a rendszer tervezésének optimalizálásában és a problémák elhárításában.
A legfontosabb teljesítménytényezők közé tartozik a levegő minősége, a hőmérséklet-változások, a terhelési jellemzők, a szerelési módszerek és a rendszernyomás stabilitása, amelyek mind jelentősen befolyásolhatják az elméleti teljesítményt.
A levegőminőség hatása az elméletre
A sűrített levegő minősége közvetlenül befolyásolja a pneumatikus hengerek teljesítményét és élettartamát. A szennyezett levegő tömítéskopást, korróziót és csökkent hatékonyságot okoz.
Levegőminőségi szabványok:
| Szennyezőanyag | Maximális szint | A teljesítményre gyakorolt hatás |
|---|---|---|
| Nedvesség | -40°F harmatpont | Megakadályozza a korróziót és a fagyást |
| Olaj | 1 mg/m³ | Csökkenti a tömítés degradációját |
| Részecskék | 5 mikron | Megakadályozza a kopást és a ragadást |
A hőmérséklet hatása a pneumatikus elméletre
A hőmérsékletváltozás befolyásolja a levegő sűrűségét, a nyomást és az alkatrészek méreteit. Ezek a változások jelentősen befolyásolhatják a hengerek teljesítményét szélsőséges környezetben.
Hőmérséklet-kompenzációs képlet: P₂ = P₁ × (T₂/T₁)
Minden 100°F hőmérséklet-emelkedés esetén a légnyomás körülbelül 20%-vel nő, ha a térfogat állandó marad. Ez befolyásolja az erőkifejtést, és ezt figyelembe kell venni a rendszer tervezésénél.
Terhelési jellemzők és dinamikus erők
A statikus és a dinamikus terhelések eltérő módon befolyásolják a hengerek teljesítményét. A dinamikus terhelések további erőket hoznak létre, amelyeket a gyorsítási és lassítási fázisokban kell leküzdeni.
Dinamikus erőelemzés:
- Gyorsító erő: F = ma (tömeg × gyorsulás)
- Súrlódási erő: Jellemzően 10-20% az alkalmazott terhelésből
- Inerciális erők: Jelentős nagy sebességnél vagy nagy terhelésnél
Nemrégiben segítettem egy Robert Chen nevű amerikai gyártónak Detroitban a nehéz autóipari alkatrészek pneumatikus rendszerének optimalizálásában. A dinamikus erők elemzésével 30%-tel csökkentettük a ciklusidőt, miközben javítottuk a pozicionálási pontosságot.
A rendszernyomás stabilitása
A nyomásingadozás befolyásolja a henger teljesítményének állandóságát. A levegő megfelelő kezelése és tárolása segít fenntartani a stabil működési feltételeket.
Nyomásstabilitási követelmények:
- Nyomásváltozás: Nem haladhatja meg a ±5% értéket az egyenletes teljesítmény érdekében.
- Vevő tartály mérete: 5-10 gallon per CFM levegőfogyasztás
- Nyomásszabályozás: ±1 PSI pontosságú alkalmazásokhoz
Hogyan hasonlítható össze a pneumatikus elmélet a hidraulikus és az elektromos rendszerekkel?
A pneumatikus elmélet más erőátviteli módszerekhez képest határozott előnyöket és korlátokat kínál. Ezeknek a különbségeknek a megértése segít a mérnököknek kiválasztani az optimális megoldásokat az adott alkalmazásokhoz.
A pneumatikus rendszerek gyors reakciót, egyszerű vezérlést és tiszta működést biztosítanak, de a hidraulikus és elektromos alternatívákhoz képest kisebb erősséggel és kevésbé pontos pozicionálással.
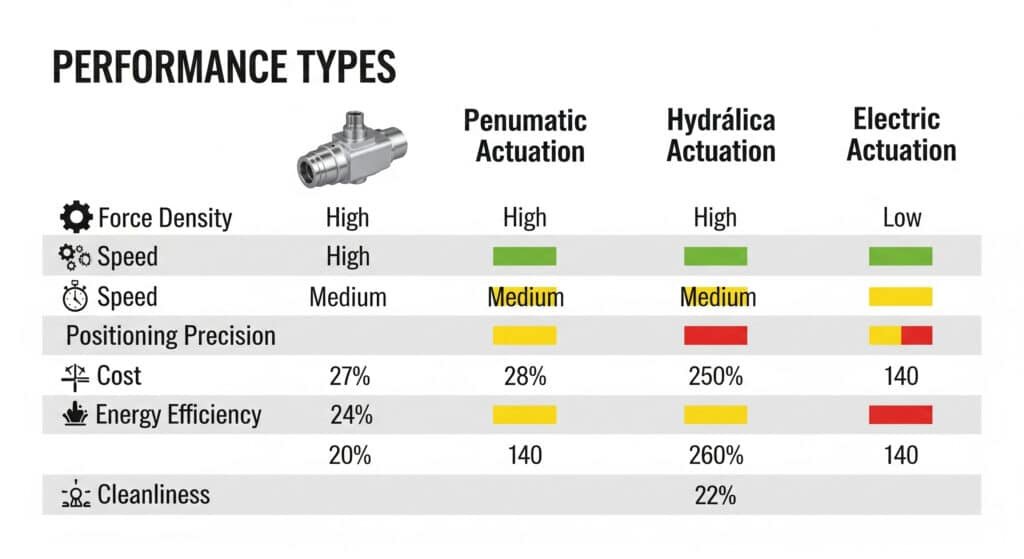
Elméleti teljesítmény-összehasonlítás
| Jellemző | Pneumatikus | Hidraulikus | Elektromos |
|---|---|---|---|
| Teljesítménysűrűség | 15-25 HP/lb | 50-100 LE/lb | 5-15 HP/lb |
| Válaszidő | 10-50 ms | 5-20 ms | 50-200 ms |
| Helymeghatározási pontosság | ±0,1 hüvelyk | ±0,01 hüvelyk | ±0,001 hüvelyk |
| Üzemi nyomás | 80-150 PSI | 1000-5000 PSI | N/A (feszültség) |
| Hatékonyság | 20-30% | 40-60% | 80-95% |
| Karbantartási gyakoriság | Alacsony | Magas | Közepes |
Energiaátalakítás hatékonyságának elmélete
A pneumatikus rendszereknek a levegő kompressziós veszteségei és a hőtermelés miatt eredendő hatékonysági korlátai vannak. Az elméleti maximális hatásfok izotermikus sűrítés esetén körülbelül 37%, de a valós rendszerek 20-30% értéket érnek el.
Energiaveszteség forrásai:
- Kompressziós hő: 60-70% bemeneti energia
- Nyomás cseppek: 5-15% rendszernyomás
- Szivárgás: 2-10% levegőfogyasztás
- Veszteségek megfékezése: Változó a vezérlési módszertől függően
Irányításelméleti különbségek
A pneumatikus vezérlés elmélete a levegő összenyomhatósága miatt jelentősen eltér a hidraulikus és az elektromos rendszerektől. Ez a tulajdonság természetes tompítást biztosít, de a pontos pozicionálást nagyobb kihívássá teszi.
Ellenőrzési jellemzők:
- Természetes megfelelés: A levegő összenyomhatósága ütéscsillapítást biztosít
- Sebességszabályozás: Inkább áramláskorlátozással, mint nyomásváltozásokkal érhető el.
- Erőszabályozás: Nehéz a nyomás/áramlás kapcsolat összetettsége miatt.
- Pozíció visszajelzés: Külső érzékelőket igényel a pontos vezérléshez
Következtetés
A pneumatikus hengerek elmélete az alapvető fizikai elveket a gyakorlati mérnöki munkával ötvözi, hogy megbízható, hatékony erőátviteli rendszereket hozzon létre világszerte számtalan ipari alkalmazásban.
GYIK a pneumatikus henger elméletéről
Mi az alapvető elmélet a pneumatikus hengerek mögött?
A pneumatikus hengerek a Pascal-törvény alapján működnek, ahol a sűrített levegő nyomása egy zárt kamrában minden irányban egyformán hat, és erőt hoz létre, amikor a nyomáskülönbségek a hengerfuratokon keresztül dugattyúkat mozgatnak.
Hogyan kell kiszámítani a pneumatikus henger erejét?
Az erő egyenlő a nyomás és a dugattyú területének szorzatával (F = P × A). Egy 4 hüvelyk átmérőjű henger 100 PSI nyomáson körülbelül 1,257 font erőt termel, levonva a súrlódást és egyéb veszteségeket.
Miért kevésbé hatékonyak a pneumatikus hengerek, mint a hidraulikus rendszerek?
A levegő összenyomhatósága energiaveszteséget okoz a sűrítési és tágulási ciklusok során, ami a pneumatikus hatékonyságot 20-30%-re korlátozza a 40-60% hatékonyságot elérő hidraulikus rendszerekhez képest.
Milyen tényezők befolyásolják a pneumatikus hengerek sebességét?
A sebesség a levegő áramlási sebességétől, a henger térfogatától, a terhelés súlyától és a nyomáskülönbségtől függ. A nagyobb áramlási sebesség és nyomás növeli a sebességet, míg a nagyobb terhelések csökkentik a gyorsulást.
Hogyan befolyásolja a hőmérséklet a pneumatikus hengerek teljesítményét?
A hőmérsékletváltozás befolyásolja a levegő sűrűségét és nyomását. Minden 100°F-os emelkedés körülbelül 20%-rel növeli a légnyomást, ami közvetlenül befolyásolja az erőteljesítményt és a rendszer teljesítményét.
Mi a különbség az egyszeresen és a kétszeresen működő hengerek elmélete között?
Az egyszeres működésű hengerek csak egy irányban használnak sűrített levegőt, rugóvisszatérítéssel, míg a kettős működésű hengerek a légnyomást használják mind a kitoló, mind a behúzó mozgásokhoz.
-
Részletes áttekintést nyújt Newton három mozgástörvényéről, amelyek a klasszikus mechanika alapelvei, és amelyek leírják a test és a rá ható erők közötti kapcsolatot, valamint az ezekre az erőkre adott mozgást. ↩
-
Részletesen ismerteti a pneumatikus rendszerek nyomásesésének okait, beleértve a csövek súrlódását, valamint a szerelvények, szelepek és szűrők veszteségeit, és elmagyarázza, hogyan csökkenti a felhasználás helyén rendelkezésre álló energiát. ↩
-
Magyarázatot ad a csiszolási eljárásra, amely egy olyan csiszoló megmunkálási eljárás, amely egy csiszolókővel történő súrolással precíziós felületet hoz létre a munkadarabon, és amelyet gyakran használnak a hengerfuratokon az olajvisszatartás érdekében egy speciális keresztsávos mintázat létrehozására. ↩
-
Ismerteti a rúd nélküli hengerek különböző kialakításait, például a mágnesesen kapcsolt és a mechanikusan kapcsolt (szalag) típusokat, és elmagyarázza a hozzájuk tartozó előnyöket, például a nagy lökethosszúságok biztosítását kompakt helyen. ↩
-
Megmagyarázza a különböző mechanizmusokat, például a fogasléces vagy lapátos kialakításokat, amelyeket a pneumatikus forgó működtetők használnak a sűrített levegőből származó lineáris erő forgómozgássá vagy nyomatékká alakítására. ↩





