
Problémái vannak a pneumatikus hengerek nem egyenletes fordulatszámával vagy a löket végének váratlan ütéseivel? Ezek a gyakori problémák gyakran a dugattyú kinematikájának rossz megértéséből erednek. Sok mérnök kizárólag az erőkövetelményekre összpontosít, miközben figyelmen kívül hagyja a rendszer teljesítményét meghatározó kritikus mozgásparamétereket.
Dugattyú kinematika1 közvetlenül befolyásolja a pneumatikus rendszer teljesítményét a nyomás-sebesség viszonyok, a gyorsulási határértékek és a csillapítási követelmények révén. Ezen elvek megértése lehetővé teszi a mérnökök számára, hogy megfelelően méretezzék az alkatrészeket, megjósolják a tényleges mozgásprofilokat, és megelőzzék a rúd nélküli hengerek és más pneumatikus működtető elemek idő előtti meghibásodását.
A Beptónál eltöltött több mint 15 év alatt, amikor pneumatikus rendszerekkel dolgoztam, számtalan olyan esetet láttam, amikor ezeknek az alapelveknek a megértése segített az ügyfeleknek megoldani a tartós teljesítményproblémákat és 3-5-ször meghosszabbítani a berendezések élettartamát.
Tartalomjegyzék
- Milyen nyomásra van valójában szüksége az állandó sebességű mozgáshoz?
- Hogyan számolja ki a maximálisan lehetséges gyorsulást a pneumatikus hengereknél?
- Miért fontos a csillapítási idő és hogyan számítják ki?
- Következtetés
- GYIK a dugattyú kinematikáról a pneumatikus rendszerekben
Milyen nyomásra van valójában szüksége az állandó sebességű mozgáshoz?
Sok mérnök egyszerűen a maximálisan elérhető nyomást alkalmazza pneumatikus rendszereiben, de ez a megközelítés nem hatékony, és rángatózó mozgáshoz, túlzott kopáshoz és energiapazarláshoz vezethet.
Az állandó sebességű mozgáshoz szükséges nyomást egy pneumatikus hengerben a P = (F + Fr)/A számítással lehet kiszámítani, ahol P a nyomás, F a külső terhelőerő, Fr a súrlódási ellenállás, A pedig a dugattyú területe. Ez a számítás biztosítja a zökkenőmentes, hatékony működést túlzott nyomás nélkül, amely energiát pazarol és felgyorsítja az alkatrészek kopását.
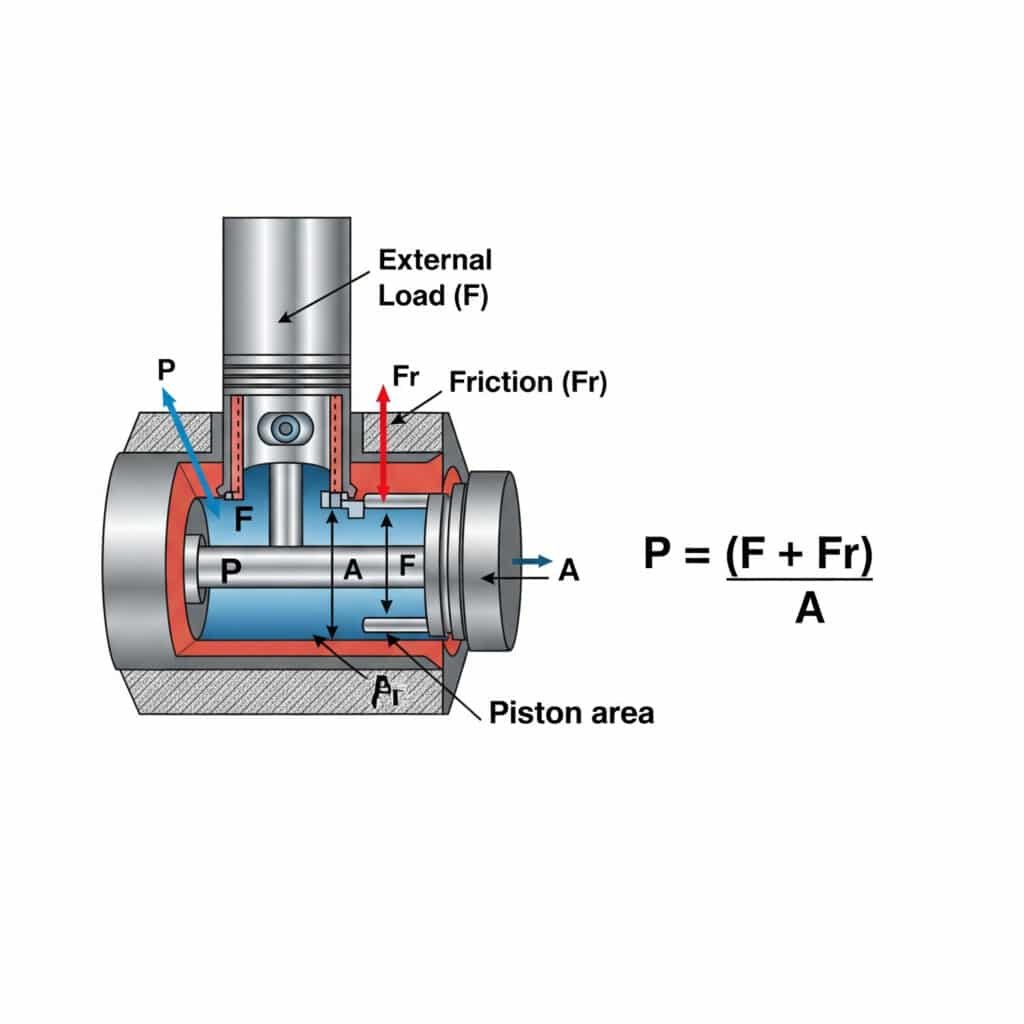
Az állandó sebességű mozgás nyomásigényének megértése gyakorlati következményekkel jár a rendszer tervezése és üzemeltetése szempontjából. Hadd bontsam le ezt megvalósítható meglátásokra.
Az állandó sebességhez szükséges nyomást befolyásoló tényezők
Az állandó sebesség fenntartásához szükséges nyomás több tényezőtől függ:
| Tényező | A nyomásigényre gyakorolt hatás | Gyakorlati megfontolás |
|---|---|---|
| Külső terhelés | Közvetlen lineáris kapcsolat | Változik a tájolástól és a külső erőktől függően |
| Súrlódás | Hozzáadódik a szükséges nyomáshoz | Változások a tömítés kopásával és kenésével |
| Dugattyú terület | Fordítottan arányos | Nagyobb furat = kisebb nyomásigény |
| Levegőellátási korlátozások | Nyomáscsökkenés a vezetékekben/szelepekben | Az alkatrészek méretezése a minimális nyomáseséshez |
| Ellennyomás | Ellenzi az indítványt | Tekintsük a kipufogógáz-áramlási kapacitást |
A stabil mozgáshoz szükséges minimális nyomás kiszámítása
A stabil mozgáshoz szükséges minimális nyomás meghatározása:
- Számítsa ki a külső terhelés leküzdéséhez szükséges erőt!
- Adjuk hozzá a súrlódási erőt (jellemzően 3-20% maximális erő).
- Osszuk el a dugattyú effektív területével
- Adjunk hozzá egy stabilitási tényezőt (jellemzően 10-30%).
Például egy 40 mm-es furatú, rúd nélküli hengerben, 10 kg-os terheléssel és 15% súrlódással:
| Paraméter | Számítás | Eredmény |
|---|---|---|
| Terhelési erő | 10kg × 9,81m/s² | 98.1N |
| Súrlódási erő | 15% maximális erő 6 bar nyomáson | ~45N |
| Teljes erő | 98,1N + 45N | 143.1N |
| Dugattyú terület | π × (0,02m)² | 0.00126m² |
| Minimális nyomás | 143,1N ÷ 0,00126m² | 113,571 Pa (1,14 bar) |
| 20% stabilitási tényezővel | 1,14 bar × 1,2 | 1,37 bar |
Valós világbeli alkalmazás: Energia-megtakarítás nyomásoptimalizálással
Tavaly együtt dolgoztam Roberttel, egy michigani bútorgyártó üzem termelési mérnökével. Az automatizált összeszerelősorán rúd nélküli hengereket használtak, amelyek terhelésre való tekintet nélkül a teljes 6 bar ellátási nyomással működtek.
Alkalmazásának elemzése után megállapítottuk, hogy a legtöbb mozgás csak 2,5-3 bar-t igényel a stabil működéshez. Azáltal, hogy arányos nyomásszabályozók, a levegőfogyasztást 40%-tal csökkentettük, miközben a ciklusidő ugyanaz maradt. Ezzel évente körülbelül $12 000 energiaköltséget takarítottunk meg, miközben csökkentettük a tömítések kopását és meghosszabbítottuk a karbantartási intervallumokat.
Sebesség-nyomás kapcsolat valós rendszerekben
A gyakorlatban a nyomás és a sebesség közötti kapcsolat nem tökéletesen lineáris a következők miatt:
- Áramláskorlátozások: A szelep és a port méretezése befolyásolja az elérhető maximális sebességet
- Összenyomhatósági hatások: A levegő összenyomható, ami gyorsulási késleltetést okoz.
- Stick-slip jelenségek: A súrlódási jellemzők a sebességgel változnak
- Inerciális hatások: A tömeg gyorsulása további erőt/nyomást igényel
Hogyan számolja ki a maximálisan lehetséges gyorsulást a pneumatikus hengereknél?
A gyorsulási határértékek megértése kulcsfontosságú a túlzott ütések, rezgések és a pneumatikus rendszerek alkatrészeinek idő előtti meghibásodásának megelőzésében.
A pneumatikus hengerben elérhető maximális gyorsulás kiszámításához a = (P × A - F - Fr)/m, ahol a a gyorsulás, P a nyomás, A a dugattyú területe, F a külső terhelés, Fr a súrlódási ellenállás és m a mozgó tömeg. Ez az egyenlet határozza meg a fizikai határait annak, hogy egy pneumatikus működtető milyen gyorsan képes elindítani vagy megállítani a mozgást.
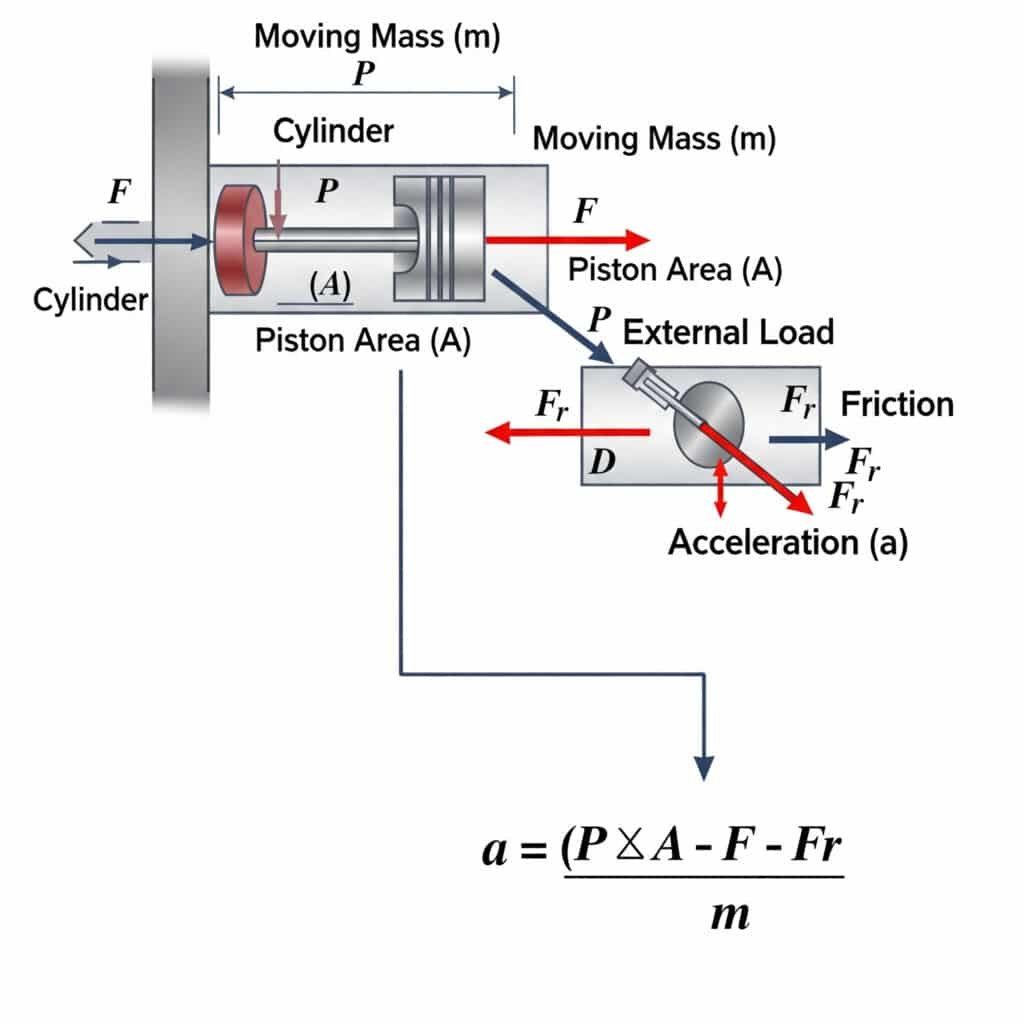
Az elméleti gyorsulási határértékek jelentős gyakorlati következményekkel járnak a rendszertervezés és az alkatrészválasztás szempontjából.
A gyorsulási határegyenlet levezetése
A gyorsulás határérték egyenlete a következő egyenletből származik Newton második törvénye2 (F = ma):
- A gyorsításhoz rendelkezésre álló nettó erő: Fnet = Fnyomás - Fterhelés - Fsúrlódás.
- Fnyomás = P × A
- Ezért: a = Fnet/m = (P × A - F - Fr)/m
Gyakorlati gyorsulási határértékek a különböző henger típusokhoz
A különböző hengerkialakítások különböző gyakorlati gyorsulási határértékekkel rendelkeznek:
| Henger típusa | Tipikus maximális gyorsulás | Korlátozó tényezők |
|---|---|---|
| Szabványos rúdhenger | 10-15 m/s² | Rúdcsavarodás, csapágyterhelések |
| Rúd nélküli henger (mágneses) | 8-12 m/s² | Mágneses csatolási erő |
| Rúd nélküli henger (mechanikus) | 15-25 m/s² | Tömítés/csapágy kialakítás, belső súrlódás |
| Vezetőhenger | 20-30 m/s² | Vezetőrendszer merevsége, teherbírás |
| Ütőhenger | 50-100+ m/s² | Kifejezetten nagy gyorsuláshoz tervezve |
Tömeggel kapcsolatos megfontolások a gyorsulásszámításokban
A gyorsulás kiszámításakor fontos, hogy minden mozgó tömeget figyelembe vegyünk:
- Dugattyú szerelvény: Tartalmazza a dugattyút, a tömítéseket és az összekötő elemeket.
- Terhelés tömege: Mozgatott külső teher
- A mozgó levegő effektív tömege: Gyakran elhanyagolható, de nagysebességű alkalmazásokban fontos.
- A szerelési alkatrészek miatt hozzáadott tömeg: Konzolok, érzékelők stb.
Egyszer segítettem egy franciaországi ügyfélnek, aki rejtélyes meghibásodásokat tapasztalt a rúd nélküli hengeres rendszerében. A henger megfelelően volt méretezve a megadott 15 kg-os terheléshez, de néhány ezer ciklus után következetesen meghibásodott.
A vizsgálat után kiderült, hogy nem számolt a szerelőlemez és a rögzítőelemek 12 kg-os tömegével. A tényleges mozgó tömeg majdnem kétszerese volt a számításainak, ami a henger tervezési határértékeit meghaladó gyorsulási erőket okozott. Egy nagyobb hengerre történő frissítés után a meghibásodások teljesen megszűntek.
Gyorsulásszabályozási módszerek
A gyorsulás biztonságos határokon belüli szabályozása:
- Áramlásszabályozó szelepek: Korlátozza az áramlási sebességet a kezdeti mozgás során
- Proporcionális szelepek: Ellenőrzött nyomásemelkedés biztosítása
- Többlépcsős gyorsítás: Fokozatos nyomásnövekedés használata
- Mechanikai csillapítás: Külső lengéscsillapítók hozzáadása
- Elektronikus vezérlés: Használja a címet. szervopneumatikus rendszerek3 gyorsulási visszajelzéssel
Miért fontos a csillapítási idő és hogyan számítják ki?
A megfelelő ütésvég-csillapítás alapvető fontosságú az ütés okozta károk megelőzése, a zaj csökkentése és a pneumatikus hengerek élettartamának meghosszabbítása szempontjából. A csillapítási idő megértése segít a mérnököknek olyan rendszerek tervezésében, amelyek egyensúlyt teremtenek a ciklusidő és az alkatrészek élettartama között.
A tompítási időt a pneumatikus hengerekben a t = √(2s/a) egyenlet segítségével számítják ki, ahol t az idő, s a tompító löket hossza, a pedig a lassulás. Ez az idő azt mutatja meg, hogy mennyi időbe telik a mozgó tömeg biztonságos lassítása az ütközés előtt, ami kritikus fontosságú a henger és a csatlakozó alkatrészek károsodásának megelőzése szempontjából.

Vizsgáljuk meg a párnázási idő számításainak gyakorlati szempontjait és a rendszertervezésre gyakorolt hatásait.
A pneumatikus párnázás fizikai háttere
Pneumatikus párnázás szabályozott légtömörítéssel és korlátozott kipufogógázzal működik:
- Ahogy a dugattyú belép a párnakamrába, a kipufogógáz útja beszűkül.
- A csapdába esett levegő összenyomódik, ami növekvő ellennyomást eredményez.
- Ez az ellennyomás olyan ellenerőt hoz létre, amely lassítja a dugattyút.
- A lassulási profil a párna kialakításától és beállításától függ.
Az optimális csillapítási idő kiszámítása
Az optimális csillapítási idő egyensúlyt teremt az ütésmegelőzés és a ciklusidő hatékonysága között:
| Paraméter | Formula | Példa |
|---|---|---|
| Tompítási távolság | A hengerek kialakítása alapján | 15mm (tipikusan 40mm-es furat esetén) |
| Szükséges lassulás | a = v²/(2s) | v=0,5m/s, s=15mm esetén: a = 8,33m/s². |
| Párnázási idő | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Nyomás felhalmozódás | P = P₀(V₀/V)^γ | A párnakamra geometriájától függ |
A párnázási teljesítményt befolyásoló tényezők
A tényleges csillapítási teljesítményt több tényező befolyásolja:
- Párnás tömítés kialakítása: Befolyásolja a légszivárgást a párnázás során.
- Tűszelep beállítása: Szabályozza a kipufogógáz-szűkítés mértékét
- Mozgó tömeg: A nehezebb terhelések hosszabb csillapítási időt igényelnek.
- Megközelítési sebesség: A nagyobb sebességek hosszabb párnatávolságot igényelnek
- Üzemi nyomás: Befolyásolja a maximálisan rendelkezésre álló ellenerőt
Párnázási típusok és alkalmazásuk
A különböző csillapítási mechanizmusok különböző alkalmazásokhoz megfelelőek:
| Párnázás típusa | Jellemzők | Legjobb alkalmazások |
|---|---|---|
| Fix párnázás | Egyszerű, nem állítható | Könnyű terhelés, egyenletes működés |
| Állítható párnázás | Tűszelepekkel hangolható | Változó terhelések, rugalmas alkalmazások |
| Önbeálló párnázás | Alkalmazkodik a különböző körülményekhez | Változó sebességek és terhelések |
| Külső lengéscsillapítók | Nagy energiaelnyelés | Nehéz terhelések, nagy sebességek |
| Elektronikus párnázás | Pontosan szabályozott lassítás | Szervopneumatikus rendszerek |
Esettanulmány: A párnázás optimalizálása nagy ciklusú alkalmazásokban
Nemrégiben együtt dolgoztam Thomasszal, aki egy németországi autóipari alkatrészgyártó cég tervezőmérnöke. A szerelősorán rúd nélküli hengereket használtak, amelyek percenként 45 ciklusonként működtek, de gyakoriak voltak a tömítések meghibásodásai és a szerelőkonzolok sérülései.
Az elemzés kimutatta, hogy a tompítási idő túl rövid volt a mozgó tömeghez képest, ami a löket mindkét végén közel 3G ütőerőt okozott. A tompító löket 12 mm-ről 20 mm-re növelésével és a tűszelep beállításainak optimalizálásával a tompítási időt 0,04 s-ról 0,07 s-ra növeltük.
Ez a látszólag apró változtatás több mint 60%-vel csökkentette az ütőerőt, teljesen megszüntette a konzol sérülését, és a tömítés élettartamát 3 hónapról több mint egy évre növelte - mindezt az előírt ciklusidő megtartása mellett.
Gyakorlati párnázási beállítási eljárás
Optimális csillapítási teljesítmény a rúd nélküli hengerekben:
- Teljesen nyitott párnaszelepekkel indítson (minimális szűkítés).
- Fokozatosan zárja a párnaszelepet, amíg egyenletes lassulás nem következik be.
- Vizsgálat minimális és maximális várható terheléssel
- Ellenőrizze a csillapítási teljesítményt a teljes sebességtartományban
- Figyeljen az ütközési hangokra, amelyek elégtelen csillapításra utalnak.
- Mérje meg a tényleges lassulási időt a számítások megerősítése érdekében.
Következtetés
A dugattyúk kinematikájának alapelveinek megértése - az állandó sebességhez szükséges nyomásigénytől a gyorsulási határértékekig és a csillapítási idő számításáig - elengedhetetlen a hatékony és megbízható pneumatikus rendszerek tervezéséhez. Ha ezeket az elveket alkalmazza rúd nélküli hengeralkalmazásaiban, optimalizálhatja a teljesítményt, csökkentheti az energiafogyasztást, és jelentősen meghosszabbíthatja az alkatrészek élettartamát.
GYIK a dugattyú kinematikáról a pneumatikus rendszerekben
Milyen nyomásra van szükségem egy adott hengerfordulatszámhoz?
A szükséges nyomás a terheléstől, a súrlódástól és a henger felületétől függ. Számítsa ki a P = (F + Fr)/A értékkel, ahol F a külső terhelőerő, Fr a súrlódási ellenállás, A pedig a dugattyú területe. Egy tipikus, 10 kg-os terhet vízszintesen mozgató, rúd nélküli henger esetében körülbelül 1,5-2 barra van szükség a stabil mozgáshoz mérsékelt sebességnél.
Milyen gyorsan tud gyorsulni egy pneumatikus henger?
Egy pneumatikus henger maximális gyorsulását a = (P × A - F - Fr)/m értékkel számoljuk ki. A tipikus rúd nélküli hengerek a kialakítástól függően 10-25 m/s² gyorsulást érhetnek el. Ez azt jelenti, hogy optimális körülmények között körülbelül 20-50 milliszekundum alatt érik el a 0,5 m/s sebességet.
Milyen tényezők korlátozzák a rúd nélküli henger maximális sebességét?
A maximális sebességet a szelep áramlási kapacitása, a levegőellátás mennyisége, a nyílások méretezése, a csillapítási képességek és a tömítés kialakítása korlátozza. A legtöbb szabványos rúd nélküli hengert 0,8-1,5 m/s maximális sebességre tervezték, bár a speciális nagysebességű kivitelek elérhetik a 2-3 m/s sebességet is.
Hogyan számítsam ki a megfelelő párnázottságot az alkalmazásomhoz?
Számítsa ki a megfelelő párnázottságot a mozgó teher mozgási energiájának (KE = ½mv²) meghatározásával és annak biztosításával, hogy a párnázási rendszer képes legyen elnyelni ezt az energiát. A csillapítási időt a t = √(2s/a) segítségével kell kiszámítani, ahol s a csillapítási távolság és a a kívánt lassulási sebesség.
Mi történik, ha a pneumatikus hengerem túl gyorsan gyorsul?
A túlzott gyorsulás mechanikai igénybevételt okozhat a rögzítőelemeken, a tömítések idő előtti kopását, fokozott rezgést és zajt, esetleges terhelésáthelyeződést vagy sérülést, valamint a rendszer pontosságának csökkenését. Rángatózó mozgáshoz is vezethet, ami a precíziós alkalmazásokban befolyásolja a termékminőséget.
Hogyan befolyásolja a terhelés irányultsága a mozgáshoz szükséges nyomást?
A terhelés irányultsága jelentősen befolyásolja a nyomásigényt. A gravitációval szemben mozgó függőleges terheknek a gravitációs erő leküzdéséhez további nyomásra van szükségük (P = F/A + Fg/A + Fr/A). A vízszintes terheknek csak a súrlódást és a tehetetlenséget kell legyőzniük. A ferde terhek a szög szinusza alapján e két szélsőérték közé esnek.
-
Alapvető magyarázatot ad a kinematikára, a mechanika azon ágára, amely a tárgyak mozgását írja le a mozgást okozó erők figyelembevétele nélkül.
elektronikus bemeneti jel, amely lehetővé teszi a fejlett pneumatikus vezérlést. ↩ -
Részletezi Newton második törvényét (F=ma), a fizika alapelvét, amely a tárgyra ható erőt a tömegével és a gyorsulásával hozza összefüggésbe, és amely minden dinamikai számítás alapja. ↩
-
Ismerteti a szervopneumatikát, egy olyan fejlett vezérlési technológiát, amely a pneumatika teljesítményét a zárt hurkú elektronikus vezérlés pontosságával ötvözi a rendkívül pontos pozicionálás és mozgásprofilok elérése érdekében. ↩



