Hogyan befolyásolja a rezgésrezonancia az ipari berendezések teljesítményét?

Minden karbantartó rémálma a berendezések váratlan meghibásodása. Amikor a gépek a saját frekvenciájukkal rezegnek, perceken belül katasztrofális károk keletkezhetnek. Láttam, hogy ez a probléma a vállalatoknak több ezer leállási időbe kerül.

Rezgés rezonancia¹ akkor fordul elő, amikor egy külső erő megegyezik egy rendszer sajátfrekvenciájával, és felerősített rezgéseket okoz, amelyek károsíthatják a berendezést. E jelenség megértése és szabályozása alapvető fontosságú a meghibásodások megelőzéséhez és a gépek élettartamának meghosszabbításához.

Hadd meséljek el egy rövid történetet. Tavaly egy németországi ügyfél pánikszerűen felhívott. A gyártósoruk leállt, mert egy rúd nélküli henger hevesen vibrált. Mi volt a probléma? A rezonancia. A cikk végére megérti, hogyan ismerheti fel és előzheti meg a hasonló problémákat a rendszereiben.

Tartalomjegyzék

Természetes frekvencia képlet: Hogyan lehet kiszámítani a rendszer sebezhető pontjait?
Mass-Spring modell: Miért olyan értékes ez az egyszerűsített megközelítés?
Csökkentési arány optimalizálása: Milyen kísérletek adják a legjobb eredményeket?
Következtetés
GYIK a rezgésrezonanciáról

Természetes frekvencia képlet: Hogyan lehet kiszámítani a rendszer sebezhető pontjait?

A berendezés saját frekvenciájának megértése az első lépés a rezonanciaproblémák megelőzése felé. Ez a kritikus érték határozza meg, hogy a rendszer mikor a legérzékenyebb a rezgési problémákra.

A sajátfrekvencia² (fn) a következő képlettel számítható ki: fn = (1/2π) × √(k/m), ahol k a merevségi együttható és m a tömeg. Ez a számítás megmutatja azt a frekvenciát, amelyen a rendszer rezonálni fog, ha megfelelő külső erőkkel gerjesztjük.

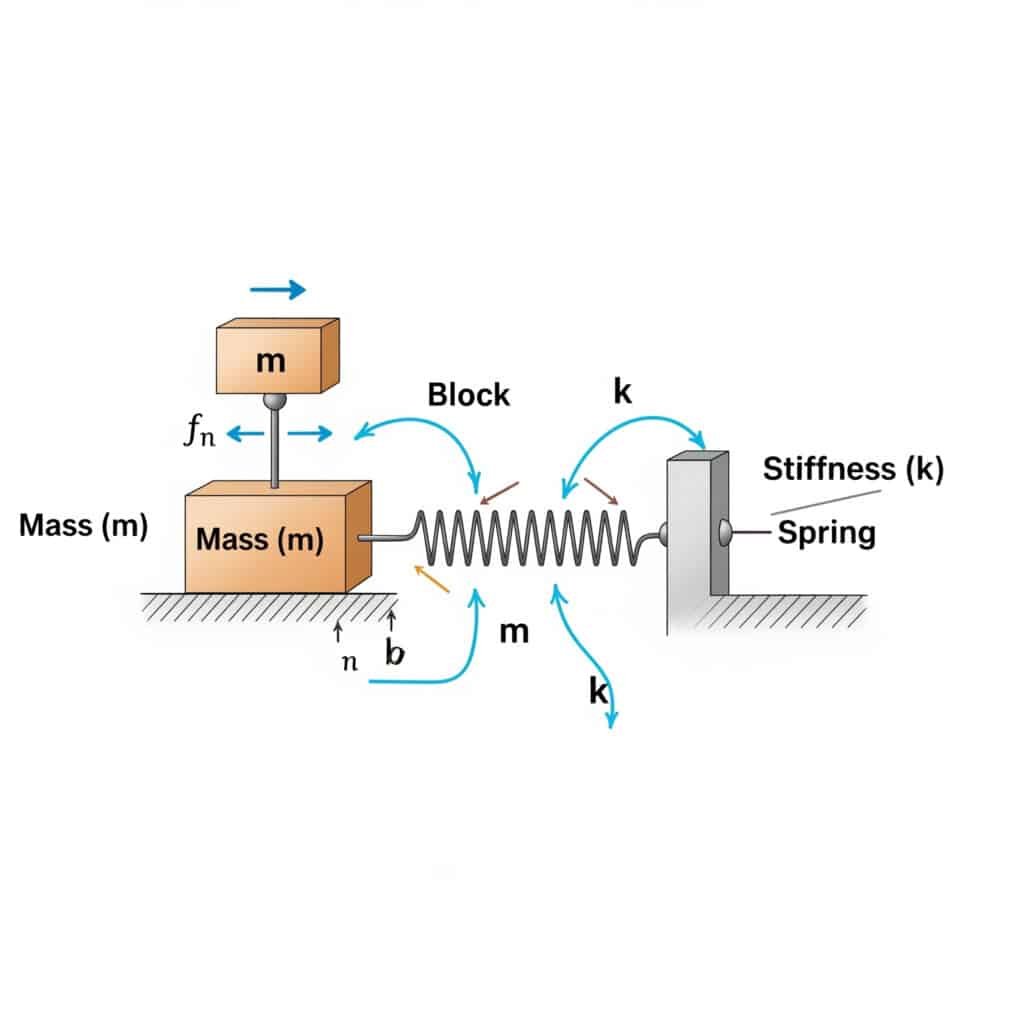
Tiszta, tanulságos diagram a sajátfrekvencia magyarázatáról. Az ábrán egy egyszerű tömeg-rugó rendszer látható, a tömbbel a "Tömeg (m)", a rugóval pedig a "Merevség (k)" feliratot viseli. A mozgásvonalak azt mutatják, hogy a rendszer oszcillál. Az ábra mellett világosan látható az "fn = (1/2π) × √(k/m)" képlet, az egyenletben szereplő "m" és "k" változókat nyilakkal összekötve a megfelelő fizikai részekkel. — sajátfrekvencia

Amikor meglátogattam egy svájci gyártóüzemet, észrevettem, hogy a rúd nélküli pneumatikus hengerek idő előtt meghibásodtak. A karbantartó csapatuk nem számította ki a beállításuk sajátfrekvenciáját. A képlet alkalmazása után megállapítottuk, hogy az üzemi sebességük veszélyesen közel volt a rendszer sajátfrekvenciájához.

A sajátfrekvencia-számítások gyakorlati alkalmazásai

A sajátfrekvencia-képlet nem csak elméleti - közvetlen alkalmazásai vannak különböző ipari környezetben:

Berendezés kiválasztása: Olyan alkatrészek kiválasztása, amelyek sajátfrekvenciája messze van az Ön üzemi körülményeitől
Megelőző karbantartás: Vizsgálatok ütemezése rezgéskockázati profilok alapján
Hibaelhárítás: A váratlan rezgések kiváltó okának azonosítása

Ipari alkatrészek közös sajátfrekvencia-értékei

Komponens	Tipikus természetes frekvenciatartomány (Hz)
Rúd nélküli hengerek	10-50 Hz
Szerelési konzolok	20-100 Hz
Támogató struktúrák	5-30 Hz
Szabályozó szelepek	40-200 Hz

A természetes frekvenciát befolyásoló kritikus tényezők

A sajátfrekvencia számítása egyszerűnek tűnik, de számos tényező bonyolíthatja a valós alkalmazásokat:

Nem egyenletes tömegeloszlás: A legtöbb ipari alkatrész nem rendelkezik tökéletesen eloszló tömeggel.
Változó merevség: Az alkatrészek merevsége különböző irányokban eltérő lehet.
Csatlakozási pontok: Az alkatrészek felszerelésének módja jelentősen befolyásolja a rezgési jellemzőket.
Hőmérsékleti hatások: Mind a tömeg, mind a merevség tulajdonságai változhatnak a hőmérséklet függvényében.

Mass-Spring modell: Miért olyan értékes ez az egyszerűsített megközelítés?

A tömeg-rugó modell intuitív keretet biztosít az összetett rezgési rendszerek megértéséhez. A bonyolult gépeket olyan alapelemekre redukálja, amelyeket a mérnökök könnyen elemezhetnek.

A tömegrugós modell³ egyszerűsíti a rezgéselemzést azáltal, hogy a mechanikai rendszereket rugókkal összekapcsolt diszkrét tömegekként ábrázolja. Ez a megközelítés lehetővé teszi a mérnökök számára a rendszer viselkedésének előrejelzését, a lehetséges rezonanciaproblémák azonosítását és hatékony megoldások kidolgozását bonyolult matematika nélkül.

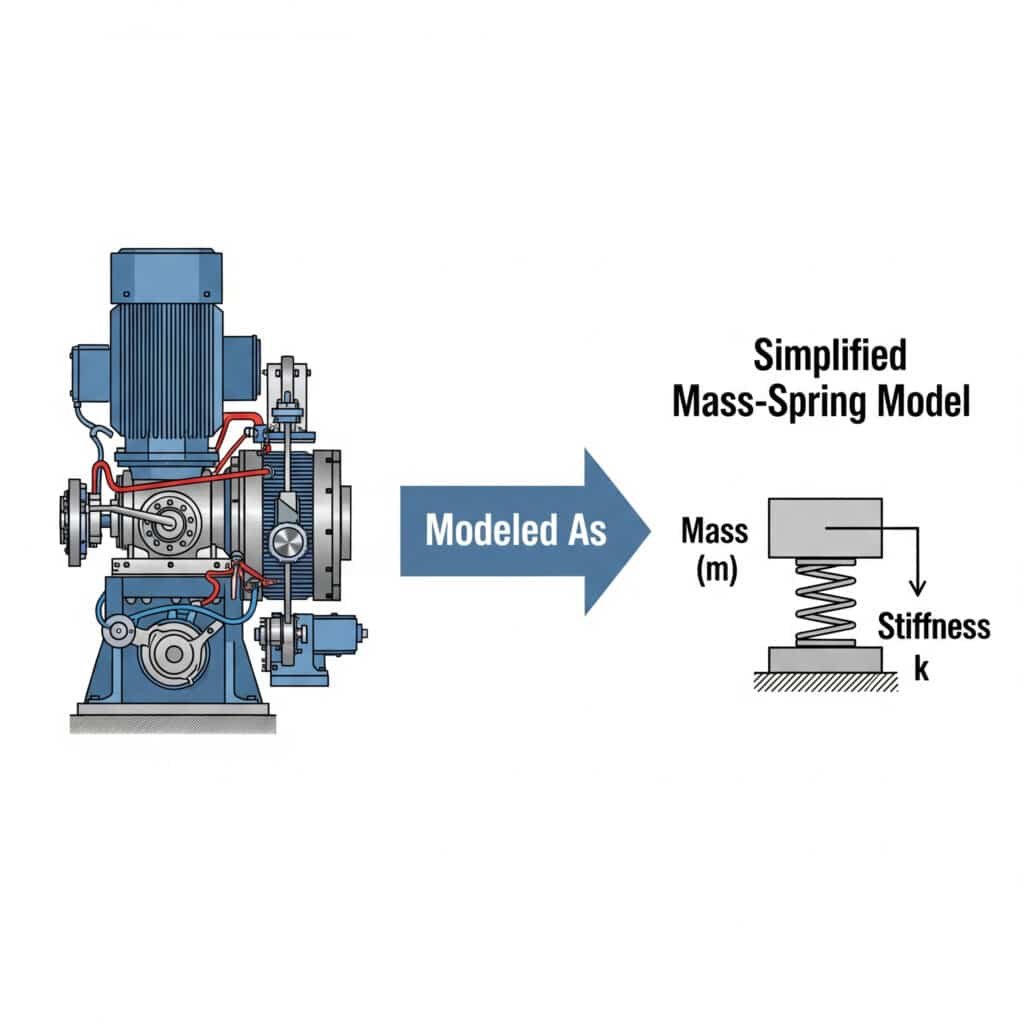
Egy összehasonlító infografika, amely a tömegrugós modellt magyarázza. A bal oldalon, az "Összetett mechanikai rendszer" címke alatt egy ipari motor részletes illusztrációja látható. Egy nagy nyíl "Modeled As" felirattal jobbra mutat. A jobb oldalon, az "Egyszerűsített tömeg-rugó modell" felirat alatt a teljes összetett motor egy egyszerű, "Tömeg (m)" feliratú blokk, amely egy egyszerű, "Merevség (k)" feliratú rugóval van összekötve. — tömegrugós modell

Emlékszem, hogy egy michigani autóalkatrész-gyártóval dolgoztam együtt, aki nem értette, hogy miért hibásodnak meg a rúd nélküli hengerek. A rendszerüket egyszerű tömeg-rugó elrendezésként modellezve azonosítottuk, hogy a rögzítő konzolok nem szándékos rugóként működtek, rezonanciaállapotot létrehozva.

Valós rendszerek átalakítása tömegrugós modellekké

Ha ezt a megközelítést szeretné alkalmazni a berendezésére:

A kulcsfontosságú tömegek azonosítása: Határozza meg, mely összetevők járulnak hozzá jelentős súllyal
A rugóelemek helyének meghatározása: Keressünk olyan alkatrészeket, amelyek energiát tárolnak és szabadítanak fel (tényleges rugók, rugalmas tartók stb.)
Térképkapcsolatok: Dokumentálja a tömegek és rugók kölcsönhatását
Egyszerűsítse a: Hasonló elemek kombinálása egy kezelhető modell létrehozásához

A tömegrugós rendszerek típusai

Rendszer típusa	Leírás	Gyakori alkalmazások
Egyetlen DOF	Egy tömeg egy rugóval	Egyszerű pneumatikus hengerek
Multi-DOF	Több tömeg több rugóval	Több alkatrészből álló összetett gépek
Folyamatos	Végtelen DOF (eltérő elemzést igényel)	Gerendák, lemezek és héjak

Haladó modellezési megfontolások

Bár az alap tömegrugós modell értékes, számos fejlesztés teszi azt még reálisabbá:

Csappantyúk hozzáadása: A valós rendszerekben mindig van energia disszipáció
A nemlinearitások figyelembevétele: A rugók nem mindig követik Hooke törvénye⁴ tökéletesen
Kényszerrezgés elszámolása: A külső erők megváltoztatják a rendszer viselkedését
Beleértve a csatolási hatásokat: Az egyik irányba történő mozgás hatással lehet más irányokra

Csökkentési arány optimalizálása: Milyen kísérletek adják a legjobb eredményeket?

A csillapítás a legjobb védelem a rezonanciaproblémák ellen. Az optimális csillapítási arány megtalálása kísérletezéssel drámaian javíthatja a rendszer teljesítményét és megbízhatóságát.

Csökkentési arány⁵ az optimalizálási kísérletek során szisztematikusan tesztelik a különböző csillapítási konfigurációkat, hogy megtalálják az ideális egyensúlyt a rezgésszabályozás és a rendszer érzékenységének javítása között. Az optimális csillapítási arány jellemzően 0,2 és 0,7 közé esik, ami elegendő rezgéscsillapítást biztosít túlzott energiaveszteség nélkül.

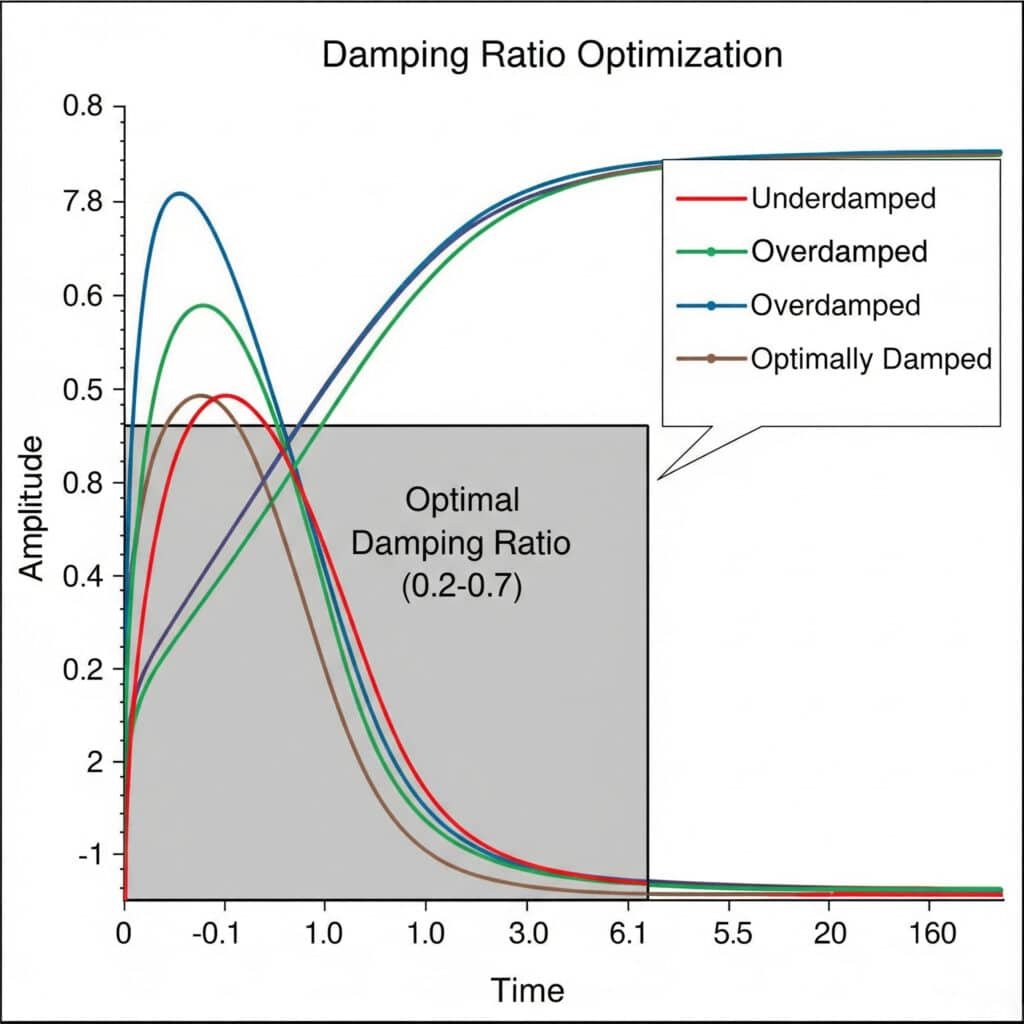
A csillapítási arány optimalizálását szemléltető grafikon a rendszer "Amplitúdó" és "Idő" függvényében. Három különböző válaszgörbét mutat: egy "alulcsillapított" görbét, amely jelentősen oszcillál, egy "túlcsillapított" görbét, amely nagyon lassan, oszcilláció nélkül tér vissza a nullához, és egy "optimálisan csillapított" görbét, amely gyorsan, minimális túlcsordulással rendeződik. Az "Optimális csillapítási arány (0,2-0,7)" feliratú árnyékolt terület kiemeli ezt az ideális választ. — csillapítási arány optimalizálása

A múlt hónapban segítettem egy franciaországi élelmiszer-feldolgozó berendezésgyártónak megoldani a mágneses rúd nélküli hengerek tartós rezgési problémáit. Egy sor csillapítási arányra vonatkozó kísérlet során felfedeztük, hogy az eredeti konstrukciójuk csillapítási aránya mindössze 0,05 volt - ez túl alacsony a rezonanciaproblémák megelőzéséhez.

Kísérleti beállítás a csillapítási arány vizsgálatához

Hatékony csillapítási optimalizálási kísérletek elvégzése:

Alapszintű mérés: A rendszer válaszának rögzítése további csillapítás nélkül
Inkrementális tesztelés: Csillapítóelemek hozzáadása szabályozott lépésekben
Válaszmérés: Amplitúdó, ülepedési idő és frekvenciaválasz mérése
Adatelemzés: Számítsa ki a csillapítási arányt minden egyes konfigurációhoz
Érvényesítés: Ellenőrizze a teljesítményt tényleges üzemi körülmények között

Csökkentési technológiák összehasonlítása

Csökkentési technológia	Előnyök	Korlátozások	Tipikus alkalmazások
Viszkózus csillapítók	Kiszámítható teljesítmény, stabil hőmérséklet	Karbantartást igényel, esetleges szivárgás	Nehézgépek, precíziós berendezések
Súrlódási csillapítók	Egyszerű kialakítás, költséghatékony	Időbeli kopás, nemlineáris viselkedés	Szerkezeti támaszok, alapgépek
Anyag csillapítás	Nincs mozgó alkatrész, kompakt	Korlátozott beállítási tartomány	Precíziós műszerek, rezgésszigetelés
Aktív csillapítás	Alkalmazkodik a változó körülményekhez	Összetett, energiát igényel	Kritikus alkalmazások, változó sebességű berendezések

A csillapítás optimalizálása különböző üzemi körülményekhez

Az ideális csillapítási arány nem univerzális - az adott alkalmazástól függ:

Nagy sebességű műveletek: Az alacsonyabb csillapítási arányok (0,1-0,3) fenntartják a reakciókészséget.
Precíziós alkalmazások: A nagyobb csillapítási arányok (0,5-0,7) stabilitást biztosítanak.
Változó terhelésű rendszerek: Adaptív csillapításra lehet szükség
Hőmérséklet-érzékeny környezetek: Vegyük figyelembe a stabil tulajdonságokkal rendelkező csillapító anyagokat

Esettanulmány: Rúd nélküli henger csillapítás optimalizálása

Amikor egy csomagológéphez optimalizáltunk egy kettős működtetésű rúd nélküli hengert, öt különböző csillapítási konfigurációt teszteltünk:

Standard végpárnák: Csökkentési arány = 0,12
Kiterjesztett párnák: Csökkentési arány = 0,25
Külső lengéscsillapítók: Csökkentési arány = 0,41
Kompozit rögzítőkonzolok: Csökkentési arány = 0,38
Kombinált megközelítés (3+4): Csökkentési arány = 0,53

A kombinált megközelítés nyújtotta a legjobb teljesítményt, 78%-vel csökkentve a rezgés amplitúdót, miközben a válaszidő elfogadható maradt.

Következtetés

A rezgésrezonancia megértése a sajátfrekvencia-számítások, a tömeg-rugó modellezés és a csillapítási arány optimalizálása révén döntő fontosságú a berendezések meghibásodásának megelőzése szempontjából. Ezen elvek alkalmazásával meghosszabbíthatja a gépek élettartamát, csökkentheti az állásidőt és javíthatja a rendszer általános teljesítményét.

GYIK a rezgésrezonanciáról

Mi a rezgésrezonancia az ipari berendezésekben?

A rezgési rezonancia akkor lép fel, amikor egy külső erő megegyezik a rendszer sajátfrekvenciájával, ami felerősített rezgéseket okoz. Az ipari berendezésekben ez a jelenség túlzott mozgáshoz, az alkatrészek kifáradásához és katasztrofális meghibásodáshoz vezethet, ha nem kezelik megfelelően.

Hogyan állapíthatom meg, hogy a rendszerem rezonanciát tapasztal-e?

Keresse az olyan tüneteket, mint a megmagyarázhatatlan zajnövekedés, látható vibráció bizonyos sebességeknél, az alkatrészek idő előtti meghibásodása és a teljesítménycsökkenés, amely állandó működési pontokon jelentkezik. A rezgéselemző eszközök megerősíthetik a rezonanciaállapotokat.

Mi a különbség a kényszerrezgés és a rezonancia között?

Erőltetett rezgés akkor keletkezik, amikor egy külső erő hat egy rendszerre, míg a rezonancia az a különleges állapot, amikor az erőltetett rezgés frekvenciája megegyezik a rendszer sajátfrekvenciájával, ami felerősített választ eredményez. Minden rezonancia kényszerrezgéssel jár, de nem minden kényszerrezgés okoz rezonanciát.

Hogyan befolyásolja egy rúd nélküli pneumatikus henger kialakítása a rezgési jellemzőket?

A rúd nélküli pneumatikus hengerek kialakítása - a mozgó kocsival, a belső tömítési rendszerrel és a vezető mechanizmusokkal - egyedi rezgési kihívásokat jelent. A meghosszabbított profil gerendaként viselkedik, amely elhajolhat, a kocsi tömege tehetetlenségi erőket hoz létre, a tömítőszalagok pedig változó súrlódást okozhatnak.

Milyen egyszerű módosításokkal csökkenthető a rezonancia a meglévő berendezésekben?

A rezonanciaproblémákkal küzdő meglévő berendezések esetében fontolja meg a tömeg hozzáadását a sajátfrekvencia megváltoztatásához, külső csillapítók vagy lengéscsillapítók beszerelését, a rögzítési módszerek módosítását a rezgésszigetelés érdekében, vagy az üzemi sebességek módosítását a rezonanciafrekvenciák elkerülése érdekében.

Alapvető magyarázatot ad a mechanikai rezonanciáról, gyakran vizuális példákkal, bemutatva, hogy egy kis periodikus erő hogyan képes nagy amplitúdójú rezgéseket előidézni egy rendszerben. ↩
Részletes betekintést nyújt a sajátfrekvencia fizikájába, vagyis abba a frekvenciába, amelyen egy rendszer bármilyen hajtó- vagy csillapító erő hiányában rezgésre hajlamos. ↩
Megmagyarázza a tömeg-rugó modell alapelveit, amely a fizikában és a mérnöki tudományokban az egyszerű harmonikus mozgást mutató összetett rendszerek elemzésére használt alapvető idealizáció. ↩
Részletek Hooke törvénye, a fizika egyik alapelve, amely szerint a rugó bizonyos távolsággal való kinyújtásához vagy összenyomásához szükséges erő egyenesen arányos a távolsággal. ↩
Leírja a csillapítási arányt, egy dimenziótlan mérőszámot, amely meghatározza, hogy a rendszerben a rezgések hogyan csökkennek egy zavar után, ami kritikus a rezonancia szabályozásához. ↩

Helló, Chuck vagyok, vezető szakértő, 15 éves tapasztalattal a pneumatikai iparban. A Bepto Pneumaticnél arra összpontosítok, hogy ügyfeleink számára kiváló minőségű, személyre szabott pneumatikai megoldásokat nyújtsak. Szakértelmem kiterjed az ipari automatizálásra, a pneumatikus rendszerek tervezésére és integrálására, valamint a kulcsfontosságú alkatrészek alkalmazására és optimalizálására. Ha bármilyen kérdése van, vagy szeretné megbeszélni projektigényeit, forduljon hozzám bizalommal a chuck@bepto.com e-mail címen.