Lassú hengerfordulatszámmal, következetlen mozgással vagy elégtelen erővel küzd a pneumatikus rendszereiben? Ezek a gyakori problémák gyakran egy félreértett okozóból erednek: az áramlási ellenállásból. Sok mérnök kizárólag a nyomás- és erőigény alapján méretezi pneumatikus alkatrészeit, figyelmen kívül hagyva az áramlási ellenállásnak a valós teljesítményre gyakorolt kritikus hatását.
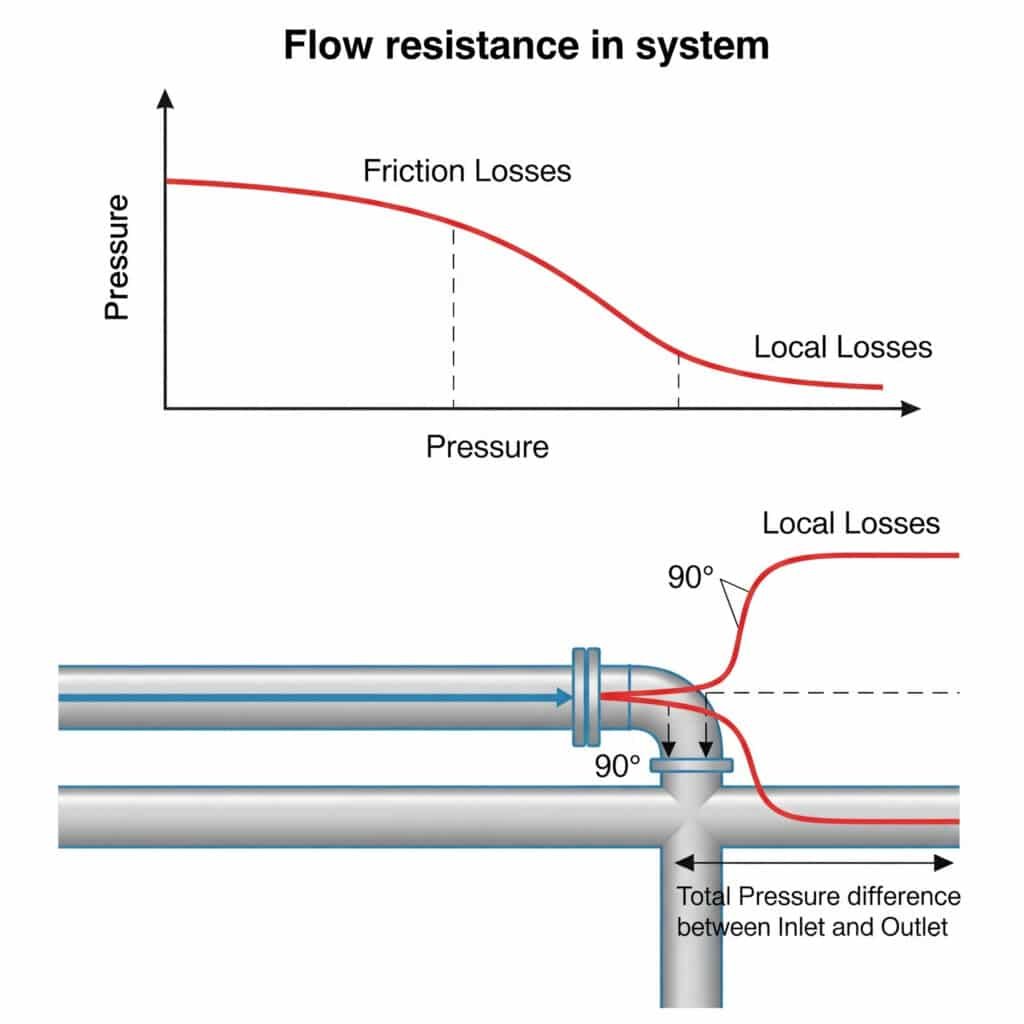
A pneumatikus rendszerekben az áramlási ellenállás olyan nyomásesést okoz, amely csökkenti a rendelkezésre álló erőt, korlátozza a maximális sebességet, és következetlen mozgást okoz. Ez az ellenállás mind az egyenes csövek mentén fellépő súrlódásból (súrlódási veszteségek), mind a szerelvényeknél, kanyarokban és szelepeknél fellépő zavarokból (helyi veszteségek) származik. Ezek az ellenállások együttesen 20-50%-vel csökkenthetik a rendszer tényleges teljesítményét az elméleti számításokhoz képest.
A Beptónál eltöltött több mint 15 év alatt, amikor pneumatikus rendszerekkel dolgoztam, számtalan olyan esetet láttam, amikor az áramlási ellenállás megértése és kezelése megbízható, hatékony működésűvé tette az alulteljesítő rendszereket. Engedje meg, hogy megosszam, mit tanultam ezeknek a rejtett teljesítménygyilkosoknak a kiszámításáról és minimalizálásáról.
Tartalomjegyzék
- Hogyan számolja ki a súrlódási veszteségeket a pneumatikus vezetékeknél?
- Miért kritikus az egyenértékű hossz módszer a pontos rendszertervezéshez?
- Mi történik, amikor a levegő átáramlik a csökkentett furatú szakaszokon?
- Következtetés
- GYIK a pneumatikus rendszerek áramlási ellenállásáról
Hogyan számolja ki a súrlódási veszteségeket a pneumatikus vezetékeknél?
Az egyenes csövek és csővezetékek súrlódási veszteségei az áramlási ellenállás számításainak alapját képezik, de sok mérnök túlságosan leegyszerűsített hüvelykujjszabályokra támaszkodik, amelyek alulméretezett rendszerekhez vezetnek.
A pneumatikus vezetékek súrlódási veszteségeinek kiszámítása a következő módszerrel történik Darcy-Weisbach-egyenlet1: ΔP = λ(L/D)(ρv²/2), ahol λ a súrlódási tényező, L a cső hossza, D a cső átmérője, ρ a levegő sűrűsége és v az áramlási sebesség. Pneumatikus rendszereknél a λ súrlódási tényező a következők alapján változik Reynolds-szám2 és a relatív érdesség, és jellemzően keresőtáblázatok vagy a Moody diagram3.
A súrlódási veszteségek megértése gyakorlati következményekkel jár a rendszer tervezésében és a hibaelhárításban. Hadd bontsam le ezt megvalósítható meglátásokra.
Súrlódási tényező táblázatok hatékony használata
A súrlódási tényező (λ) a legfontosabb paraméter a nyomásesés kiszámításában, de értékének meghatározásához figyelembe kell venni az áramlási körülményeket:
| Áramlási rendszer | Reynolds-szám (Re) | Súrlódási tényező meghatározása |
|---|---|---|
| Lamináris áramlás | Re < 2000 | λ = 64/Re |
| Átmeneti áramlás | 2000 < Re < 4000 | Megbízhatatlan - kerülje a tervezést ebben a tartományban |
| Turbulens áramlás | Re > 4000 | A relatív érdességen (ε/D) alapuló keresőtáblázatok használata |
Gyakorlati súrlódási tényező kereső táblázat
A pneumatikus rendszerek turbulens áramlásához használja ezt az egyszerűsített táblázatot:
| Cső anyaga | Relatív érdesség (ε/D) | Súrlódási tényező (λ) általános Reynolds-számok mellett |
|---|---|---|
| Re = 10,000 | ||
| Sima csövek (PVC, poliuretán) | 0.0001 – 0.0005 | 0.031 |
| Alumínium csövek | 0.001 – 0.002 | 0.035 |
| Horganyzott acél | 0.003 – 0.005 | 0.042 |
| Rozsdás acél | 0.01 – 0.05 | 0.054 |
A nyomásesés kiszámítása valós pneumatikus rendszerekben
Nézzünk egy gyakorlati példát:
| Paraméter | Érték/számítás | Példa |
|---|---|---|
| Csőátmérő (D) | Belső átmérő | 8mm (0,008m) |
| Cső hossza (L) | Teljes egyenes hossza | 5m |
| Áramlási sebesség (Q) | A rendszerkövetelményekből | 20 szabványos liter/másodperc |
| Levegő sűrűsége (ρ) | Üzemi nyomáson | 7,2 kg/m³ 6 bar nyomáson |
| Áramlási sebesség (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Reynolds-szám (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1,273,600 |
| Relatív érdesség | Poliuretán csövekhez | 0.0003 |
| Súrlódási tényező (λ) | A keresőtáblából | 0.017 |
| Nyomásesés (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Valós világbeli alkalmazás: A henger sebességével kapcsolatos problémák megoldása
Tavaly együtt dolgoztam Sarah-val, aki egy wisconsini csomagolóeszközöket gyártó vállalatnál dolgozott. Az ő rúd nélküli hengeres rendszere a várt sebességnek csak 60% sebességgel működött, annak ellenére, hogy rendelkezett a megfelelő méretű hengerrel és megfelelő ellátási nyomással.
Miután elemeztem a rendszerét, rájöttem, hogy 6 mm-es csöveket használ nagy áramlású alkalmazáshoz. A súrlódási veszteségek 2,1 bar nyomásesést okoztak, ami jelentősen csökkentette a rendelkezésre álló erőt és sebességet. A 10 mm-es csövekre való átállással a nyomásesést 0,4 barra csökkentettük, és a rendszere azonnal elérte a kívánt teljesítményt minden egyéb változtatás nélkül.
A súrlódási veszteségeket befolyásoló tényezők valós rendszerekben
A tényleges súrlódási veszteségeket több tényező befolyásolja:
- A levegő hőmérséklete: A magasabb hőmérséklet növeli a viszkozitást és a súrlódást
- Szennyezés: A szennyeződés és az olaj növelheti az effektív érdességet
- Csőhajlítás: A hajlított csövek mikrodeformációja növeli az ellenállást
- Az életkor romlása: A korrózió és a lerakódások idővel növelik az érdességet
- Üzemi nyomás: A nagyobb nyomás növeli a sűrűséget és a veszteségeket
Miért kritikus az egyenértékű hossz módszer a pontos rendszertervezéshez?
A szerelvényeknél, szelepeknél és kanyarokban fellépő helyi veszteségek gyakran meghaladják az egyenes csövek súrlódási veszteségeit, mégis sok mérnök vagy figyelmen kívül hagyja őket, vagy durva becslési módszereket alkalmaz, amelyek teljesítményproblémákhoz vezetnek.
Az egyenértékű hossz módszer a szerelvényekből és szelepekből származó helyi veszteségeket egyenértékű egyenes csőhosszúságra számítja át, amely ugyanazt a nyomásesést okozná. Ezt a Le = K(D/λ) számítással kell kiszámítani, ahol Le az egyenértékű hosszúság, K a helyi veszteség együttható4, D a cső átmérője, λ pedig a súrlódási tényező. Ez a módszer egyszerűsíti a számításokat és pontosabb rendszerteljesítmény-előrejelzéseket biztosít.
Vizsgáljuk meg, hogyan lehet ezt a módszert hatékonyan alkalmazni a pneumatikus rendszerek tervezésénél.
Egyenértékű hosszúsági táblázatok a gyakori pneumatikus alkatrészekhez
Íme egy praktikus referenciatáblázat a gyakori pneumatikus alkatrészekről:
| Komponens | K-érték | Ekvivalens hossz (Le/D) |
|---|---|---|
| 90°-os könyök (éles) | 0.9 | 30 |
| 90°-os könyök (standard sugár) | 0.3 | 10 |
| 45°-os könyök | 0.2 | 7 |
| T-csomópont (átfolyás) | 0.3 | 10 |
| T-csomópont (elágazás) | 1.0 | 33 |
| Golyósszelep (teljesen nyitott) | 0.1 | 3 |
| Kapu szelep (teljesen nyitva) | 0.2 | 7 |
| Gyorscsatlakozó | 0.4-0.8 | 13-27 |
| Visszacsapó szelep | 1.5-2.5 | 50-83 |
| Szabványos áramlásszabályozó szelep | 1.0-3.0 | 33-100 |
Az egyenértékű hossz módszer alkalmazása
A módszer hatékony használatához:
- A pneumatikus áramkör összes alkatrészének azonosítása
- Keresse meg a K-értéket vagy az egyenértékű hosszarányt (Le/D) minden egyes alkatrész esetében.
- Számítsa ki az egyenértékű hosszúságot a csőátmérővel való szorzással.
- Adja hozzá az összes egyenértékű hosszúságot a tényleges egyenes csőhosszhoz.
- Használja a teljes effektív hosszúságot a súrlódási veszteség számításaihoz.
Például egy 5 m hosszú, egyenes 8 mm-es csőből, valamint négy 90°-os könyökből, egy T-csomópontból és két gyorscsatlakozóból álló rendszer:
| Komponens | Mennyiség | Le/D | Egyenértékű hossz |
|---|---|---|---|
| 90°-os könyök | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| T-csomópont | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Gyorscsatlakozók | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Teljes egyenértékű hossz | 0.72m | ||
| Tényleges egyenes hossza | 5.00m | ||
| Teljes effektív hossz | 5.72m |
Ez azt jelenti, hogy az Ön 5 m-es rendszere a helyi veszteségek miatt valójában úgy viselkedik, mint egy 5,72 m-es rendszer - 14,41 TP3T effektív hossznövekedés.
Esettanulmány: A szelepek elhelyezésének optimalizálása összeszerelő rendszerekben
Nemrég segítettem Miguelnek, egy arizonai elektronikai összeszerelő üzem automatizálási mérnökének. A pick-and-place rendszerében következetlen mozgást és ciklusidő-ingadozást tapasztaltak, annak ellenére, hogy kiváló minőségű alkatrészeket használtak.
Az elemzés kimutatta, hogy a szelepelosztója 3 méterre volt a palackoktól, és az áramkör számos szerelvényt tartalmazott. Az egyenértékű hosszszámítás azt mutatta, hogy a 3 m-es tényleges távolság a helyi veszteségek miatt 7,2 m-es tényleges hosszúságot jelentett - ez több mint kétszerese az egyenes cső távolságának!
A szelepelosztó közelebb helyezésével a hengerekhez és számos szerelvény megszüntetésével a tényleges hosszúságot 7,2 méterről 2,1 méterre csökkentettük. Ez 70%-tel csökkentette a nyomásesést, ami egyenletes mozgást és 15%-tel a ciklusidő csökkenését eredményezte.
Gyakorlati tippek a helyi veszteségek minimalizálására
A pneumatikus rendszerek helyi veszteségeinek csökkentése érdekében:
- Söpört vagy lekerekített könyökök használata éles kanyarok helyett (csökkenti a K-értéket 67%-vel)
- A szerelvények számának minimalizálása közvetlenebb útvonaltervezéssel
- Válasszon alacsony súrlódású alkatrészeket mint például a teljes furatú golyóscsapok, ahol szükséges
- A szerelvények megfelelő méretezése - az alulméretezett szerelvények aránytalanul nagy veszteségeket okoznak
- A szelepek elhelyezése a működtetőkhöz közel a tényleges csőhossz minimalizálása érdekében
Mi történik, amikor a levegő átáramlik a csökkentett furatú szakaszokon?
A pneumatikus áramkörökben a csökkentett furatú szakaszok - például részben zárt szelepek, alulméretezett szerelvények vagy átmérő átmenetek - jelentős áramláskorlátozásokat hoznak létre, amelyek súlyosan befolyásolhatják a rendszer teljesítményét.
Amikor a levegő csökkentett furatú szakaszokon áramlik át, nyomásesések5 a ΔP = ρ(v₂² - v₁²)/2 képlet szerint következik be, ahol v₁ a korlátozás előtti sebesség és v₂ a korlátozásban lévő sebesség. Ez a C = (1 - (d/D)⁴) furatarány-kompenzációs tényezővel kompenzálható, ahol d a csökkentett átmérő és D az eredeti átmérő. Ez a tényező segít a rendszer tényleges teljesítményének előrejelzésében és az alkatrészek alulméretezésének elkerülésében.
Vizsgáljuk meg a csökkentett furatszelvények gyakorlati következményeit, és azt, hogyan lehet ezeket figyelembe venni a rendszertervezés során.
Nyomásesések kiszámítása átmérőátmeneteknél
Ha a levegő egy nagyobb átmérőjűből egy kisebb átmérőjűbe áramlik, a nyomásesés a következő módszerrel számítható ki:
| Paraméter | Formula | Példa |
|---|---|---|
| Eredeti átmérő (D) | A specifikációkból | 10mm |
| Csökkentett átmérő (d) | A specifikációkból | 6mm |
| Furatarány (d/D) | Egyszerű osztás | 0.6 |
| Áramlási sebesség (Q) | A rendszerkövetelményekből | 15 szabványos liter/másodperc |
| Sebesség az eredeti csőben (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Sebesség a szűkített szakaszon (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Nyomásesés (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Kompenzációs tényező (C) | C = (1 - (d/D)⁴) | 0.87 |
Gyakori furatcsökkentési forgatókönyvek és hatásuk
Itt látható, hogy a különböző furatcsökkentések hogyan befolyásolják az áramlási kapacitást:
| Furat csökkentése | Áramlási kapacitás csökkentése | A nyomásesés növekedése |
|---|---|---|
| 10 mm és 8 mm között | 36% | 2.4× |
| 10 mm és 6 mm között | 64% | 7.7× |
| 10 mm és 4 mm között | 84% | 39× |
| 8 mm és 6 mm között | 44% | 3.2× |
| 8 mm és 4 mm között | 75% | 16× |
| 6 mm és 4 mm között | 56% | 5.1× |
Ezek a számok rávilágítanak arra, hogy az átmérő látszólag csekély mértékű csökkentése miért lehet drámai hatással a rendszer teljesítményére.
A többszörös korlátozások kumulatív hatása
A valódi pneumatikus áramkörökben több korlátozás sorban fordul elő. Hatásuk halmozottan jelentkezik, és a következőkkel számítható ki:
- Az egyes korlátozások átalakítása a megfelelő C-tényezőre
- Számítsa ki a teljes C-tényezőt: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Használja ezt a teljes tényezőt a rendszer teljes teljesítménycsökkenésének meghatározásához.
Esettanulmány: A szelep és a működtető közötti eltérés problémáinak megoldása
A múlt hónapban Thomasszal, egy észak-karolinai bútorgyártó üzem karbantartási felügyelőjével dolgoztam együtt. Az új rúd nélküli hengeres rendszere a várt sebesség kevesebb mint felével működött, annak ellenére, hogy a gyártó által ajánlott szelepméretet használta.
A vizsgálat többszörös furatcsökkenést tárt fel az áramkörében:
- 10 mm-es tápvezeték 8 mm-es szelepnyílásokhoz (C₁ = 0,36)
- 8 mm-es szelepnyílások 6 mm-es szerelvényekhez (C₂ = 0,44)
- 6 mm-es szerelvények 8 mm-es hengernyílásokhoz belső korlátozásokkal (C₃ = 0,32)
A teljes kompenzációs tényező Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75 volt, ami azt jelenti, hogy a rendszere 75% elméleti áramlási kapacitását veszítette el!
Azáltal, hogy az egész rendszerben megfelelően méretezett alkatrészeket alkalmaztunk, megszüntettük ezeket a korlátozásokat, és a kívánt teljesítményt a palack vagy az ellátási nyomás megváltoztatása nélkül értük el.
Gyakorlati stratégiák a furatcsökkentési veszteségek minimalizálására
A fúráscsökkentésből származó veszteségek csökkentése:
- Az alkatrészek következetes méretezése az egész pneumatikus körfolyamatban
- Használja a legnagyobb gyakorlati csőméretet nagy áramlási sebességű alkalmazásokhoz
- Figyeljen a belső alkatrészkorlátozásokra, nem csak a csatlakozási méretek
- Tekintsük a párhuzamos áramlási utakat nagy áramlási követelményekhez
- Szükségtelen adapterek és átmenetek kiküszöbölése ahol csak lehetséges
A "leggyengébb láncszem" elve a pneumatikus rendszerekben
Ne feledje, hogy a pneumatikus rendszer teljesítményét a legkorlátozóbb alkatrész korlátozza. Egyetlen alulméretezett elem semlegesítheti a rendszer más részein megfelelően méretezett alkatrészek előnyeit.
Például egy 10 mm-es csövekkel, 10 mm-es szelepekkel, de 6 mm-es szerelvényekkel ellátott rendszer a palacknál lényegében ugyanolyan teljesítményt nyújt, mint egy 6 mm-es alkatrészeket tartalmazó rendszer - magasabb költségek mellett.
Következtetés
Az áramlási ellenállás megértése és megfelelő kiszámítása - a súrlódási tényező táblázatok, az egyenértékű hosszmódszerek és a csökkentett furat kompenzációja révén - elengedhetetlen a valós körülmények között elvárt teljesítményt nyújtó pneumatikus rendszerek tervezéséhez. E számítási módszerek és tervezési elvek alkalmazásával optimalizálhatja rúd nélküli hengeres alkalmazásait és más pneumatikus rendszereit a maximális teljesítmény és megbízhatóság érdekében.
GYIK a pneumatikus rendszerek áramlási ellenállásáról
Mekkora nyomásesés elfogadható egy pneumatikus rendszerben?
Az elfogadható nyomásesés az alkalmazás követelményeitől függ, de általános iránymutatásként a hatékony működés érdekében a teljes nyomásesést a tápfeszültségi nyomás 10-15% értékére kell korlátozni. Egy 6 baros rendszer esetében ez azt jelenti, hogy a teljes nyomásesést 0,6-0,9 bar alatt kell tartani. A kritikus alkalmazások még alacsonyabb, 5-8% nyomásesést is igényelhetnek az egyenletes teljesítmény fenntartásához.
Mi a kapcsolat a csőátmérő és a nyomásesés között?
A nyomásesés fordítottan arányos az átmérő ötödik hatványával (D⁵) a pneumatikus rendszerek turbulens áramlása esetén. Ez azt jelenti, hogy a csőátmérő megduplázása körülbelül 32-szeresére csökkenti a nyomásesést. Például a 6 mm-es cső átmérőjének 12 mm-re történő növelése 1,5 barról mindössze 0,047 barra csökkentheti a nyomásesést ugyanolyan áramlási körülmények között.
Hogyan határozhatom meg a megfelelő csőméretet a pneumatikus alkalmazásomhoz?
Válassza ki a csőméretet az áramlási követelmények és az elfogadható nyomásesés alapján. Számítsa ki a Reynolds-számot és a súrlódási tényezőt, majd használja a Darcy-Weisbach-egyenletet a nyomásesés meghatározásához különböző átmérők esetén. Válassza ki azt a legkisebb átmérőt, amely a nyomásesést az elfogadható határokon belül tartja (általában <10% a tápfeszültségi nyomáson), figyelembe véve a helyszűke és a költségvonzatokat.
Mi okoz nagyobb korlátozást: egy 90°-os könyök vagy 5 méter egyenes cső?
Egy éles 90°-os könyök jellemzően 30 csőátmérőnyi egyenes csővel egyenértékű ellenállást okoz. A 8 mm-es csövek esetében egy éles könyök körülbelül 240 mm (30 × 8 mm) egyenes csőnek felel meg. Ez azt jelenti, hogy 5 méter egyenes cső körülbelül 21-szer nagyobb korlátozást okoz, mint egyetlen könyök. A rendszerek azonban gyakran több könyököt és szerelvényt tartalmaznak, amelyek együttes hatása meghaladhatja az egyenes csőhosszúságú veszteségeket.
Hogyan befolyásolják a gyorscsatlakozó szerelvények a rendszer teljesítményét?
A szabványos gyorscsatlakozó szerelvények általában 15-25 csőátmérőnyi egyenes csővel egyenértékű helyi veszteséget okoznak. Ennél is jelentősebb, hogy sok gyorscsatlakozónak a névleges méreténél kisebb belső korlátozása van. Egy "10 mm-es" gyorscsatlakozó belső szűkítése lehet, hogy csak 7-8 mm, ami olyan furatcsökkenést eredményez, amely az áramlási kapacitást 50-70%-vel csökkentheti ezen a ponton.
Milyen hatással vannak a részben zárt áramlásszabályozó szelepek a rendszer teljesítményére?
A teljes furatfelületének 50%-ig lezárt áramlásszabályozó szelep nem csak 50%-vel csökkenti az áramlást - az átmérő és az áramlási kapacitás közötti nem lineáris kapcsolat miatt körülbelül 75%-vel csökkenti az áramlást. A nyomásesés a sebességváltozás négyzetének megfelelően nő, így a hatásos átmérő felére csökkentése azonos áramlási feltételek mellett körülbelül 16-szorosára növeli a nyomásesést.
-
Részletesen bemutatja a Darcy-Weisbach-egyenletet, amely a folyadékdinamikában alapvető és széles körben használt képlet a csőben fellépő súrlódás miatti nyomásveszteség kiszámítására. ↩
-
Világosan meghatározza a Reynolds-számot, egy kritikus dimenziótlan mennyiséget, amelyet különböző folyadékáramlási helyzetekben az áramlási mintázatok (lamináris vagy turbulens) előrejelzésére használnak. ↩
-
Bemutatja a Moody-diagramot, egy átfogó grafikont, amely a Darcy-súrlódási tényezőt a Reynolds-szám és a relatív érdesség függvényében ábrázolja, és amely a mérnökök szabványos eszköze a csövekben fellépő nyomásesés meghatározásához. ↩
-
Ismerteti a K-érték vagy helyi veszteségtényező fogalmát, amely egy dimenziótlan szám, amelyet a csőszerelvény vagy szelep nyomásveszteségének jellemzésére használnak az egyenértékű hossz módszer részeként. ↩
-
Részletesen ismerteti a folyadék szűkületen (nyíláson) való áthaladásakor fellépő nyomásesés fizikai alapjait, a folytonossági egyenlet és a Bernoulli-elv elve alapján. ↩



