
Azt látja, hogy az energiaszámlái emelkednek, miközben a pneumatikus rendszerei nem teljesítenek megfelelően? Nincs egyedül. Több mint 15 éve dolgozom ipari pneumatikával, és láttam, hogy a vállalatok több ezer dollárt pazarolnak el a nem hatékony rendszerekre. A probléma gyakran a pneumatikus teljesítményszámítások alapvető félreértéséből fakad.
A pneumatikus teljesítményszámítás a léghajtású rendszerek energiafogyasztásának, erőfejlesztésének és hatékonyságának szisztematikus meghatározása. A megfelelő modellezés magában foglalja a bemeneti teljesítményt (kompresszor energiája), az átviteli veszteségeket és a kimeneti teljesítményt (ténylegesen elvégzett munka), lehetővé téve a mérnökök számára a nem hatékony működés azonosítását és a rendszer teljesítményének optimalizálását.
Tavaly meglátogattam egy pennsylvaniai gyártóüzemet, ahol gyakori meghibásodásokat tapasztaltak a rúd nélküli hengeres rendszereikben. A karbantartó csapatuk értetlenül állt a következetlen teljesítmény előtt. A megfelelő pneumatikus teljesítményszámítások alkalmazása után felfedeztük, hogy mindössze 37% hatásfokkal működtek! Hadd mutassam meg, hogyan kerülheti el a hasonló buktatókat az Ön működésében.
Tartalomjegyzék
- Elméleti teljesítmény: Milyen egyenletek vezérlik a pontos pneumatikus számításokat?
- Hatékonysági veszteségek lebontása: Hová megy valójában a pneumatikus energiája?
- Energia-visszanyerési potenciál: Mennyi energiát nyerhet vissza a rendszeréből?
- Következtetés
- GYIK a pneumatikus teljesítményszámításokról
Elméleti teljesítmény: Milyen egyenletek vezérlik a pontos pneumatikus számításokat?
A pneumatikus rendszer által leadható elméleti maximális teljesítmény megértése minden optimalizálási erőfeszítés alapja. Ezek az egyenletek adják azt a viszonyítási alapot, amelyhez képest a tényleges teljesítményt mérik.
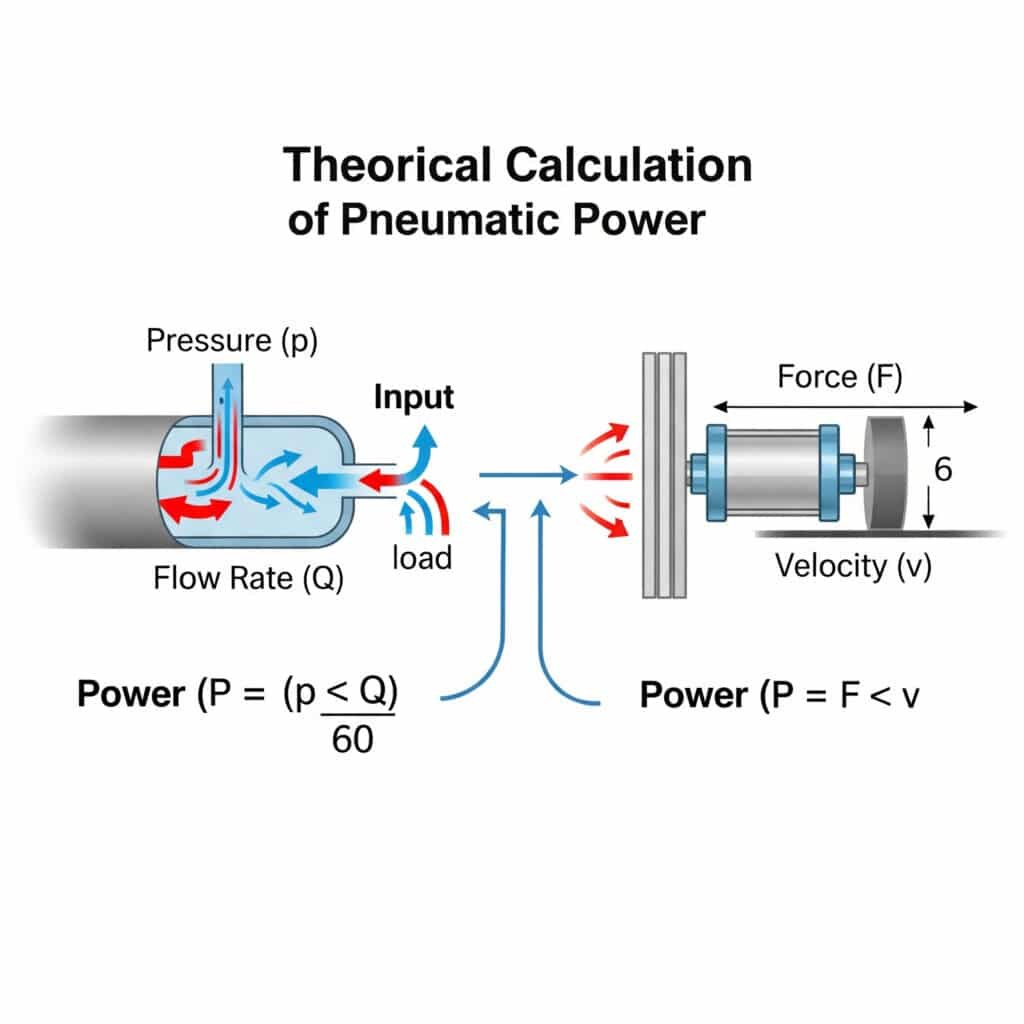
Egy pneumatikus rendszer elméleti teljesítménye a P = (p × Q)/60 egyenlet segítségével számítható ki, ahol P a teljesítmény kilowattban, p a nyomás barban, Q pedig az áramlási sebesség m³/percben. A lineáris működtetők, például a rúd nélküli hengerek esetében a teljesítmény egyenlő az erő és a sebesség szorzatával (P = F × v), ahol az erő a nyomás és az effektív terület szorzata.
Emlékszem, amikor egy ohiói élelmiszer-feldolgozó berendezésgyártónak adtam tanácsot, aki nem értette, miért van szükség a pneumatikus rendszereikhez ekkora kompresszorokra. Amikor alkalmaztuk az elméleti teljesítményegyenleteket, rájöttünk, hogy a rendszerük kialakítása kétszer akkora teljesítményt igényelt, mint amekkorát eredetileg számítottak. Ez az egyszerű matematikai tévedés több ezer forintjukba került a működési hatékonyság hiánya miatt.
Pneumatikus alapteljesítmény egyenletek
Bontsuk le a különböző komponensek alapvető egyenleteit:
Kompresszorokhoz
A kompresszor által igényelt bemeneti teljesítmény a következőképpen számítható ki:
P₁ = (Q × p × ln(p₂/p₁)) / (60 × η)
Hol:
- P₁ = bemeneti teljesítmény (kW)
- Q = légáram (m³/perc)
- p₁ = bemeneti nyomás (abszolút bar)
- p₂ = kimeneti nyomás (abszolút bar)
- η = A kompresszor hatásfoka
- ln = Természetes logaritmus1
Lineáris működtetőkhöz (beleértve a rúd nélküli hengereket is)
A lineáris hajtás kimeneti teljesítménye:
P₂ = F × v
Hol:
- P₂ = kimenő teljesítmény (W)
- F = erő (N) = p × A
- v = sebesség (m/s)
- p = üzemi nyomás (Pa)
- A = effektív terület (m²)
Az elméleti számításokat befolyásoló tényezők
| Tényező | Az elméleti teljesítményre gyakorolt hatás | Beállítási módszer |
|---|---|---|
| Hőmérséklet | 1% változás 3°C-onként | Szorozzuk meg (T₁/T₀) |
| Magasság | ~1% 100 m tengerszint feletti magasságonként | Állítsa be a légköri nyomást |
| Páratartalom | Akár 3% magas páratartalom mellett | Gőznyomás-korrekció alkalmazása |
| Gázösszetétel | A szennyeződésektől függően változik | A fajlagos gázállandók használata |
| Ciklusidő | Befolyásolja az átlagos teljesítményt | Számítsa ki az üzemi ciklustényezőt |
Speciális teljesítménymodellezési megfontolások
Az alapegyenleteken túl számos tényező mélyebb elemzést igényel:
Izotermikus vs. adiabatikus folyamatok
A valódi pneumatikus rendszerek valahol a kettő között működnek:
- Izotermikus folyamat2: A hőmérséklet állandó marad (lassabb folyamatok)
- Adiabatikus folyamat: Nincs hőátadás (gyors folyamatok)
A legtöbb ipari alkalmazásnál, ahol rúd nélküli hengerek vannak, a folyamat működés közben közelebb van az adiabatikushoz, ami az adiabatikus egyenlet használatát teszi szükségessé:
P = (Q × p₁ × (κ/(κ-1)) × [(p₂/p₁)^((κ-1)/κ) - 1]) / 60
Ahol κ a hőkapacitási arány (levegő esetében körülbelül 1,4).
Dinamikus válasz modellezése
Nagy sebességű alkalmazások esetén a dinamikus válasz kritikussá válik:
- Gyorsítási fázis: Nagyobb teljesítményigény a sebességváltások során
- Állandósult fázis: A szabványos egyenleteken alapuló konzisztens teljesítmény
- Lassítási fázis: Az energia visszanyerésének lehetősége
Gyakorlati alkalmazási példa
Dupla működtetésű rúd nélküli hengerhez:
- Furatátmérő: 40mm
- Üzemi nyomás: 6 bar
- Lökethossz: 500mm
- Ciklusidő: 2 másodperc
Az elméleti teljesítményszámítás a következő lenne:
- Erő = nyomás × terület = 6 × 10⁵ Pa × π × (0,02)² m² = 754 N
- Sebesség = távolság/idő = 0,5m / 1s = 0,5 m/s (egyenlő kihúzási/visszahúzási időt feltételezve).
- Teljesítmény = erő × sebesség = 754 N × 0,5 m/s = 377 W
Ez az elméleti maximális kimenő teljesítményt jelenti, mielőtt a rendszer hatékonysági hiányosságait figyelembe vennénk.
Hatékonysági veszteségek lebontása: Hová megy valójában a pneumatikus energiája?
Az elméleti és a tényleges pneumatikus teljesítmény közötti különbség gyakran megdöbbentő. Ha pontosan tudjuk, hol veszik el az energia, az segít a fejlesztési erőfeszítések rangsorolásában.
A pneumatikus rendszerek hatásfokveszteségei jellemzően az elméleti számítások 10-30% értékére csökkentik a tényleges teljesítményt. A főbb veszteségkategóriák közé tartozik a kompressziós hatástalanság (15-20%), az elosztási veszteségek (10-30%), a vezérlőszelepek korlátozása (5-10%), a mechanikai súrlódás (10-15%) és a nem megfelelő méretezés (akár 25%), amelyek mindegyike szisztematikusan kezelhető.
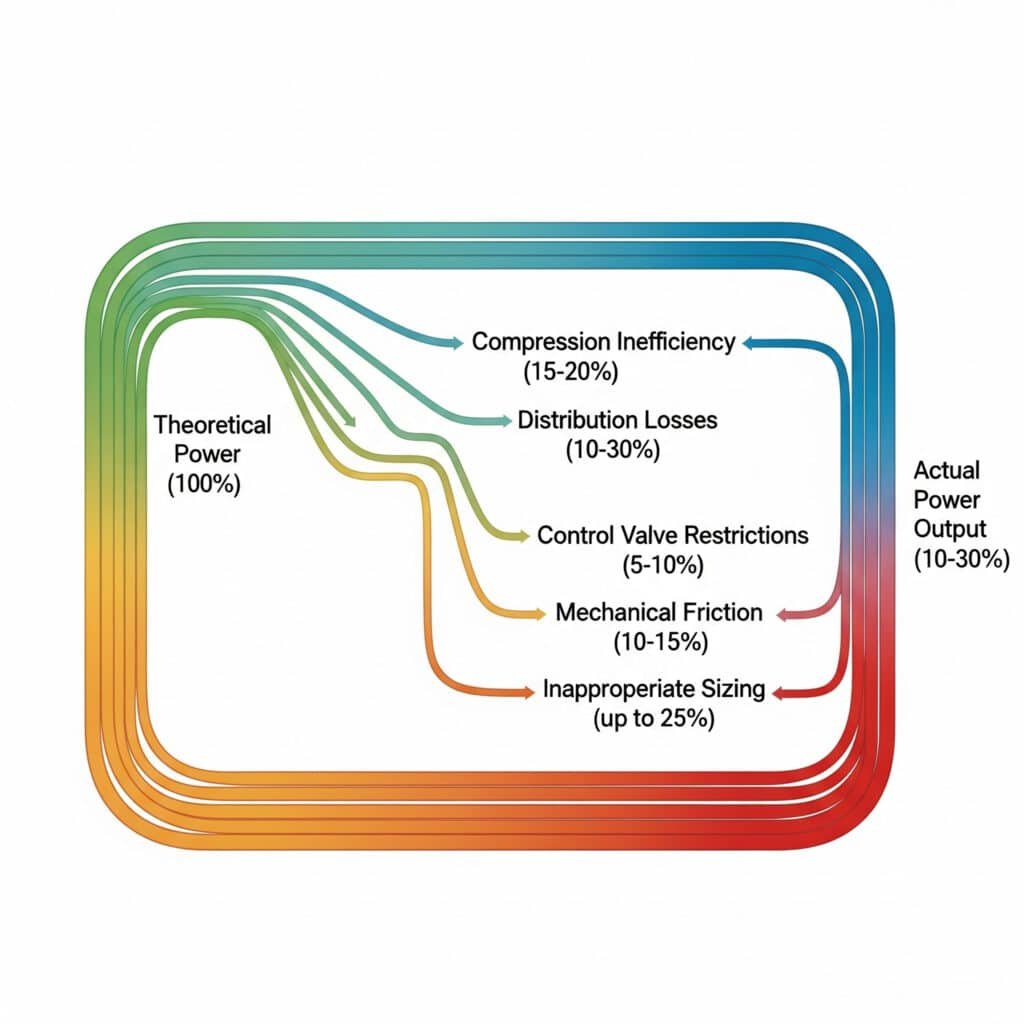
Egy torontói gyártóüzem energiaauditja során felfedeztük, hogy a pneumatikus rúd nélküli hengeres rendszerük mindössze 22% hatékonysággal működött. Az egyes veszteségforrások feltérképezésével olyan célzott fejlesztési tervet dolgoztunk ki, amely nagyobb tőkebefektetés nélkül megduplázta a hatékonyságot. Az üzem vezetője megdöbbent, hogy ilyen jelentős megtakarítás származott a látszólag jelentéktelen problémák kezeléséből.
Átfogó hatékonysági veszteség feltérképezése
Ahhoz, hogy igazán megértsük a rendszerét, minden veszteséget számszerűsíteni kell:
Termelési veszteségek (kompresszor)
| Veszteség típusa | Tipikus tartomány | Elsődleges okok |
|---|---|---|
| A motor hatástalansága | 5-10% | Motor kialakítása, kora, karbantartása |
| Kompressziós hő | 15-20% | Termodinamikai korlátok |
| Súrlódás | 3-8% | Mechanikai tervezés, karbantartás |
| Szivárgás | 2-5% | Tömítés minősége, karbantartás |
| Ellenőrzési veszteségek | 5-15% | Nem megfelelő ellenőrzési stratégiák |
Elosztási veszteségek (csőhálózat)
| Veszteség típusa | Tipikus tartomány | Elsődleges okok |
|---|---|---|
| Nyomáscsökkenés | 3-10% | Csőátmérő, hosszúság, kanyarok |
| Szivárgás | 10-30% | Csatlakozás minősége, kora, karbantartás |
| Kondenzáció | 2-5% | Nem megfelelő szárítás, hőmérséklet-ingadozás |
| Nem megfelelő nyomás | 5-15% | Túl nagy rendszernyomás az alkalmazáshoz |
Végfelhasználói veszteségek (működtetők)
| Veszteség típusa | Tipikus tartomány | Elsődleges okok |
|---|---|---|
| Szelep korlátozások | 5-10% | Alulméretezett szelepek, összetett áramlási útvonalak |
| Mechanikai súrlódás | 10-15% | Tömítés kialakítása, kenés, igazítás |
| Nem megfelelő méretezés | 10-25% | Túlméretezett/alulméretezett alkatrészek |
| Kipufogógáz áramlás | 10-20% | Ellennyomás, korlátozott kipufogógáz |
A valós hatékonyság mérése
A rendszer tényleges hatékonyságának kiszámításához:
Hatékonyság (%) = (Tényleges kimeneti teljesítmény / elméleti bemeneti teljesítmény) × 100
Például, ha a kompresszor 10 kW elektromos energiát fogyaszt, de a rúd nélküli henger csak 1,5 kW mechanikai munkát végez:
Hatékonyság = (1,5 kW / 10 kW) × 100 = 15%
Hatékonyság-optimalizálási stratégiák
A több száz pneumatikus rendszerrel kapcsolatos tapasztalataim alapján a következők a leghatékonyabb fejlesztési megközelítések:
A termelés hatékonysága érdekében
- Optimális nyomás kiválasztása: Minden 1 bar csökkentés körülbelül 7% energiát takarít meg.
- Változó sebességű meghajtók3: A kompresszor kimeneti teljesítménye az igényekhez igazodik
- Hővisszanyerés: A kompressziós hő elnyerése létesítményi felhasználásra
- Rendszeres karbantartás: Különösen légszűrők és intercoolerek
Az elosztás hatékonysága érdekében
- Szivárgás felderítése és javítása4: Gyakran 10-15% azonnali megtakarítást eredményez.
- Nyomás Zónázás: Különböző nyomásszintek biztosítása különböző alkalmazásokhoz
- Cső méretezés optimalizálása: A nyomásesés minimalizálása a megfelelő méretezéssel
- Rövidzárlat megszüntetése: Biztosítani kell, hogy a levegő a legközvetlenebb úton jusson el a felhasználási helyig.
Végfelhasználói hatékonyság
- Megfelelő alkatrész méretezés: A működtető méretének hozzáigazítása a tényleges erőigényhez
- Szelep elhelyezése: A szelepek elhelyezése a működtetőkhöz közel
- Kipufogógáz visszanyerése: Ahol lehetséges, a kipufogógázok levegőjét felfogni és újra felhasználni
- Súrlódáscsökkentés: A mozgó alkatrészek megfelelő beállítása és kenése
Energia-visszanyerési potenciál: Mennyi energiát nyerhet vissza a rendszeréből?
A legtöbb pneumatikus rendszer használat után az értékes sűrített levegőt a légkörbe engedi. Ennek az energiának az összegyűjtése és újrafelhasználása jelentős lehetőséget jelent a hatékonyság javítására.
A pneumatikus rendszerek energia-visszanyerése a bemeneti energia 10-40% részét nyerheti vissza olyan technológiák révén, mint a zárt körfolyamatok, a kipufogógáz újrahasznosítása és a nyomásfokozás. A visszanyerési potenciál a ciklus jellemzőitől, a terhelési profiloktól és a rendszer kialakításától függ, a legnagyobb nyereséget a gyakori leállással és egyenletes terhelési mintákkal rendelkező rendszereknél lehet elérni.
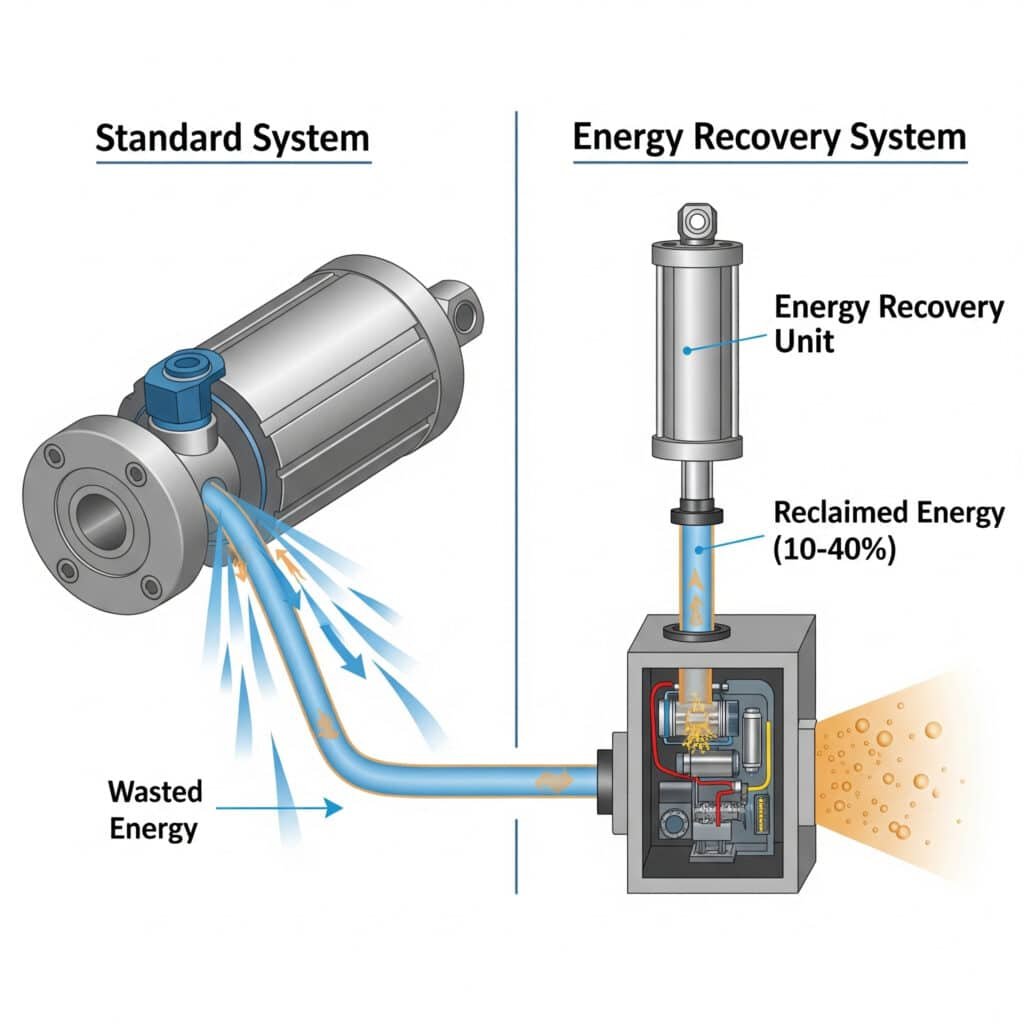
Nemrégiben egy wisconsini csomagolóberendezés-gyártóval dolgoztam együtt, hogy energia-visszanyerést valósítsunk meg a nagy sebességű, rúd nélküli pneumatikus hengeres sorokon. Azáltal, hogy a kipufogógázok levegőjét elnyertük és újra felhasználtuk a visszatérő lökésekhez, 27%-vel csökkentettük a sűrített levegő fogyasztásukat. A rendszer mindössze 7 hónap alatt megtérült - sokkal gyorsabban, mint az eredetileg tervezett 18 hónap.
Energiakihasználási technológiák értékelése
A különböző helyreállítási megközelítések különböző előnyökkel járnak:
Zárt hurkú áramkörök tervezése
Ez a megközelítés a levegő elszívása helyett a levegőt keringeti vissza:
- Működési elv: A kinyújtó löketből származó levegő visszahúzó löketet biztosít
- Visszaszerzési potenciál: 20-30% a rendszer energiája
- Legjobb alkalmazások: Kiegyensúlyozott terhelés, kiszámítható ciklusok
- Végrehajtás bonyolultsága: Mérsékelt (a rendszer átalakítása szükséges)
- ROI Időkeret: Általában 1-2 év
Kipufogógáz levegő újrahasznosítása
Elszívja a kipufogógázt másodlagos alkalmazásokhoz:
- Működési elv: Elszívott levegőt alacsonyabb nyomású alkalmazásokhoz vezetni
- Visszaszerzési potenciál: 10-20% a rendszer energiája
- Legjobb alkalmazások: Vegyes nyomásigény, többzónás létesítmények
- Végrehajtás bonyolultsága: Alacsony vagy közepes (további csővezetékekre van szükség)
- ROI Időkeret: Gyakran 1 év alatt
Nyomásfokozás
A kipufogógáz levegő felhasználása a nyomás növelésére más műveletekhez:
- Működési elv: Elszívott levegő meghajtók nyomásfokozó5 nagynyomású igényekhez
- Visszaszerzési potenciál: 15-25% a megfelelő alkalmazásokhoz
- Legjobb alkalmazások: Nagy és kisnyomású rendszerek
- Végrehajtás bonyolultsága: Mérsékelt (nyomásfokozót igényel)
- ROI Időkeret: 1-3 év a használati profiltól függően
Energia-visszanyerési potenciál számítása
A rendszer helyreállítási potenciáljának becslése:
Visszanyerhető energia (%) = Kibocsátási energia × visszanyerési hatásfok × hasznosítási tényező
Hol:
- Kipufogási energia = A levegő tömege × fajlagos energia a kipufogási körülmények között
- Visszanyerési hatásfok = technológia-specifikus hatásfok (jellemzően 40-70%)
- Hasznosítási tényező = A gyakorlatban hasznosítható elszívott levegő százalékos aránya
Esettanulmány: Rúd nélküli henger energia-visszanyerése
Mágneses rúd nélküli hengereket használó gyártósorhoz:
| Paraméter | A helyreállítás előtt | A helyreállítás után | Megtakarítás |
|---|---|---|---|
| Levegőfogyasztás | 850 L/min | 620 L/min | 27% |
| Energia költség | $12,400/év | $9,050/év | $3,350/év |
| Rendszer hatékonysága | 18% | 24.6% | 6.6% javulás |
| Ciklusidő | 2,2 másodperc | 2,2 másodperc | Nincs változás |
| Végrehajtás költsége | – | $19,500 | 5,8 hónapos megtérülés |
A helyreállítási potenciált befolyásoló tényezők
Számos változó határozza meg, hogy mennyi energiát tudsz gyakorlatilag visszanyerni:
Ciklus jellemzői
- Munkaciklus: Nagyobb regenerálódási potenciál gyakori kerékpározással
- Megállási idő: A hosszabb tartózkodási idő csökkenti a helyreállítási lehetőségeket
- Sebesség követelmények: A nagyon nagy sebesség korlátozhatja a helyreállítási lehetőségeket
Terhelési profil
- Terhelés konzisztencia: Az egyenletes terhelés jobb helyreállítási potenciált kínál
- Inerciális hatások: A nagy tehetetlenségű rendszerek visszanyerhető energiát tárolnak
- Irányváltozások: A gyakori visszafordulások növelik a helyreállítási potenciált
Rendszertervezési korlátozások
- Térbeli korlátozások: Egyes visszanyerési rendszerek további alkatrészeket igényelnek
- Hőmérséklet érzékenység: A visszanyerő rendszerek befolyásolhatják az üzemi hőmérsékletet
- Irányítás bonyolultsága: A fejlett helyreállítás kifinomult ellenőrzéseket igényel
Következtetés
A pneumatikus teljesítményszámítások elsajátítása az elméleti modellezés, a hatékonyságveszteség-elemzés és az energia-visszanyerés értékelése révén átalakíthatja a rendszer teljesítményét. Ezen elvek alkalmazásával csökkentheti az energiafogyasztást, meghosszabbíthatja az alkatrészek élettartamát és javíthatja az üzemi megbízhatóságot - mindezt jelentős költségcsökkentés mellett.
GYIK a pneumatikus teljesítményszámításokról
Mennyire pontosak az elméleti pneumatikus teljesítményszámítások?
Az elméleti számítások általában 85-95% pontosságot biztosítanak, ha minden változót megfelelően figyelembe vesznek. Az eltérés fő forrásai közé tartoznak a termodinamikai modellek egyszerűsítései, a valós gázok viselkedésének eltérései és az állandósult állapotú egyenletekben nem rögzített dinamikus hatások. A legtöbb ipari alkalmazás esetében ezek a számítások elegendő pontosságot biztosítanak a rendszer tervezéséhez és optimalizálásához.
Mekkora az ipari pneumatikus rendszerek átlagos hatékonysága?
Az ipari pneumatikus rendszerek átlagos hatásfoka 10% és 30% között mozog, a legtöbb rendszer 15-20% hatásfok körül működik. Ez az alacsony hatásfok a több átalakítási lépésből adódik: elektromosból mechanikussá a motorban, mechanikussá a kompresszorban, majd pneumatikussá a működtető egységekben, és vissza mechanikussá a működtető egységekben, és minden egyes szakaszban veszteségek keletkeznek.
Hogyan határozhatom meg, hogy az energia-visszanyerés gazdaságilag életképes-e a rendszerem számára?
Számítsa ki a potenciális megtakarítást úgy, hogy megszorozza az éves sűrítettlevegős energiaköltségét a becsült hasznosítási százalékkal (általában 10-30%). Ha ez az éves megtakarítás és a megvalósítási költség hányadosa két év alatti megtérülési időt eredményez, akkor a hasznosítás általában megvalósítható. A nagy üzemi ciklusú, kiszámítható terhelésű és évi $10 000-et meghaladó sűrítettlevegő-költségű rendszerek a legjobb jelöltek.
Mi a kapcsolat a nyomás, az áramlás és a teljesítmény között a pneumatikus rendszerekben?
A teljesítmény (P) egy pneumatikus rendszerben egyenlő a nyomás (p) és az áramlási sebesség (Q) szorzatával, osztva az időállandóval: P = (p × Q)/60 (P kW-ban, p bar-ban, Q pedig m³/perc-ben). Ez azt jelenti, hogy a teljesítmény lineárisan nő a nyomással és az áramlási sebességgel. A növekvő nyomás azonban exponenciálisan nagyobb kompresszorteljesítményt igényel, így a nyomáscsökkentés általában hatékonyabb, mint az áramláscsökkentés.
Hogyan befolyásolja a henger mérete a rúd nélküli pneumatikus rendszerek energiafogyasztását?
A henger mérete közvetlenül befolyásolja az energiafogyasztást az effektív felületén keresztül. A furat átmérőjének megduplázása megnégyszerezi a területet, és így megnégyszerezi a levegőfogyasztást és a teljesítményigényt azonos nyomás mellett. A nagyobb hengerek azonban gyakran alacsonyabb nyomáson működnek ugyanolyan erőkifejtés mellett, ami potenciálisan energiát takaríthat meg. A megfelelő méretezés magában foglalja a henger területének a tényleges erőigényhez való igazítását, ahelyett, hogy túlméretezett alkatrészeket használna.
-
Világos magyarázatot ad a természetes logaritmusról (ln), amely matematikai függvény kulcsfontosságú a pneumatikus rendszerek izotermikus kompressziója során végzett munka pontos kiszámításához. ↩
-
Részletesen ismerteti az izotermikus (állandó hőmérsékletű) és az adiabatikus (hőátadás nélküli) folyamatok közötti különbségeket, amelyek a termodinamikában a gázok sűrítésének és tágulásának modellezésére használt két elméleti végletet jelentik. ↩
-
Elmagyarázza a változó fordulatszámú hajtások (VSD-k) működési elveit, amelyek a kompresszorok hatékonyságának javítására szolgáló kulcsfontosságú technológiát jelentenek a motor fordulatszámának az ingadozó levegőigényhez való pontos igazítása révén. ↩
-
Gyakorlati információkat nyújt az ipari csővezetékek légszivárgásainak felderítésére használt különböző technikákról és eszközökről, ami kritikus karbantartási tevékenység a pneumatikus rendszerek energiapazarlásának csökkentése érdekében. ↩
-
Leírja a nyomásfokozó (vagy nyomásfokozó) mechanikáját, egy olyan eszközét, amely egy alacsony nyomású levegővel hajtott nagy felületű dugattyút használ, hogy egy kisebb dugattyúval nagyobb nyomást hozzon létre, lehetővé téve az energia visszanyerését. ↩


