
Nehezen tudja megjósolni a pneumatikus henger tényleges teljesítményét? Sok mérnök tévesen számítja ki az erőkifejtést és a nyomásigényt, ami rendszerhibákhoz és költséges állásidőhöz vezet. De van egy egyszerű módja annak, hogy elsajátítsa ezeket a számításokat.
A pneumatikus hengerek alapvető fizikai alapelvek szerint működnek, elsősorban Pascal törvénye1, amely szerint a zárt folyadékra kifejtett nyomás minden irányban egyformán terjed. Ez lehetővé teszi, hogy a hengererő kiszámítását a nyomás és a dugattyú effektív területének szorzataként végezzük, az áramlási sebességek és a nyomásegységek pontos átváltást igényelnek a pontos rendszertervezéshez.
Több mint egy évtizede segítek az ügyfeleknek pneumatikus rendszereik optimalizálásában, és láttam, hogy ezen alapelvek megértése hogyan változtathatja meg a rendszer megbízhatóságát. Engedje meg, hogy megosszam önnel a gyakorlati tudást, amely segít elkerülni a gyakori hibákat, amelyeket nap mint nap látok.
Tartalomjegyzék
- Hogyan határozza meg a Pascal-törvény a henger erőterhelését?
- Mi az összefüggés a légáramlás és a hengerek nyomása között?
- Miért kritikus a nyomásegységek átváltásának megértése a rendszertervezéshez?
- Következtetés
- GYIK a pneumatikus rendszerek fizikájáról
Hogyan határozza meg a Pascal-törvény a henger erőterhelését?
A Pascal-törvény megértése alapvető fontosságú bármely pneumatikus rendszerben a hengerek teljesítményének előrejelzéséhez és optimalizálásához.
Pascal törvénye kimondja, hogy a folyadékra zárt rendszerben gyakorolt nyomás egyenletesen terjed a folyadékban. A pneumatikus hengerek esetében ez azt jelenti, hogy a leadott erő egyenlő a nyomás és a dugattyú effektív területének szorzatával (F = P × A). Ez az egyszerű összefüggés az alapja minden hengererő-számításnak.

Az erőszámítás származtatása
Bontsuk le a hengererő-számítások matematikai levezetését:
Alapvető erőegyenlet
A hengererő alapvető egyenlete a következő:
F = P × A
Hol:
- F = kimenő erő (N)
- P = nyomás (Pa)
- A = hatásos dugattyúfelület (m²)
Hatékony területre vonatkozó megfontolások
A hatásos terület a henger típusától és irányától függően változik:
| Henger típusa | Hosszabbító erő | Visszahúzó erő |
|---|---|---|
| Egyszeri működésű | P × A | Csak a rugóerő |
| Dupla működésű (standard) | P × A | P × (A - a) |
| Dupla működésű (rúd nélküli) | P × A | P × A |
Hol:
- A = Teljes dugattyúfelület
- a = a rúd keresztmetszeti területe
Egyszer konzultáltam egy ohiói gyártóüzemmel, amely nem tapasztalt elégséges erőt a préselő alkalmazásukban. A számításaik papíron helyesnek tűntek, de a tényleges teljesítmény nem volt megfelelő. A vizsgálat során rájöttem, hogy mérőnyomás2 a számításaikban az abszolút nyomás helyett, és nem számoltak a rúd behúzás közbeni területével. A helyes képlettel és nyomásértékekkel történő újraszámítás után sikerült megfelelően méretezni a rendszerüket, és 23%-vel növelni a termelékenységet.
Gyakorlati erőszámítási példák
Vizsgáljunk meg néhány valós számítást:
Példa 1: Nyújtóerő egy szabványos hengerben
Egy henger esetében:
- Furatátmérő = 50mm (sugár = 25mm = 0,025m)
- Üzemi nyomás = 6 bar (600 000 Pa)
A dugattyú területe:
A = π × r² = π × (0,025)² = 0,001963 m²
A meghosszabbító erő:
F = P × A = 600 000 Pa × 0,001963 m² = 1178 N ≈ 118 kg erő.
2. példa: Visszahúzó erő ugyanabban a hengerben
Ha a rúd átmérője 20 mm (sugár = 10 mm = 0,01 m):
A rúd területe:
a = π × r² = π × (0,01)² = 0,000314 m²
A hatékony behúzási terület:
A - a = 0,001963 - 0,000314 = 0,001649 m²
A visszahúzó erő:
F = P × (A - a) = 600,000 Pa × 0.001649 m² = 989 N ≈ 99 kg erő
Hatékonysági tényezők valós alkalmazásokban
A gyakorlati alkalmazásokban számos tényező befolyásolja az elméleti erőszámítást:
Súrlódási veszteségek
A dugattyútömítés és a hengerfal közötti súrlódás csökkenti a tényleges erőt:
| Pecsét típusa | Tipikus hatékonysági tényező |
|---|---|
| Standard NBR | 0.85-0.90 |
| Alacsony súrlódású PTFE | 0.90-0.95 |
| Elöregedett/kopott tömítések | 0.70-0.85 |
Gyakorlati erőegyenlet
Egy pontosabb, a valóságban érvényes erőegyenlet a következő:
F_tényleges = η × P × A
Hol:
- η (eta) = Hatékonysági tényező (jellemzően 0,85-0,95)
Mi az összefüggés a légáramlás és a hengerek nyomása között?
Az áramlási sebesség és a nyomás közötti kapcsolat megértése kulcsfontosságú a levegőellátó rendszerek méretezéséhez és a hengerek fordulatszámának előrejelzéséhez.
A pneumatikus rendszerekben a légáramlás és a nyomás fordítottan arányos - mivel a nyomás növekedésével az áramlás jellemzően csökken. Ez az összefüggés a gáztörvényeket követi, és a korlátozások, a hőmérséklet és a rendszer térfogata befolyásolja. A henger megfelelő működése megköveteli e tényezők kiegyensúlyozását a kívánt sebesség és erő elérése érdekében.
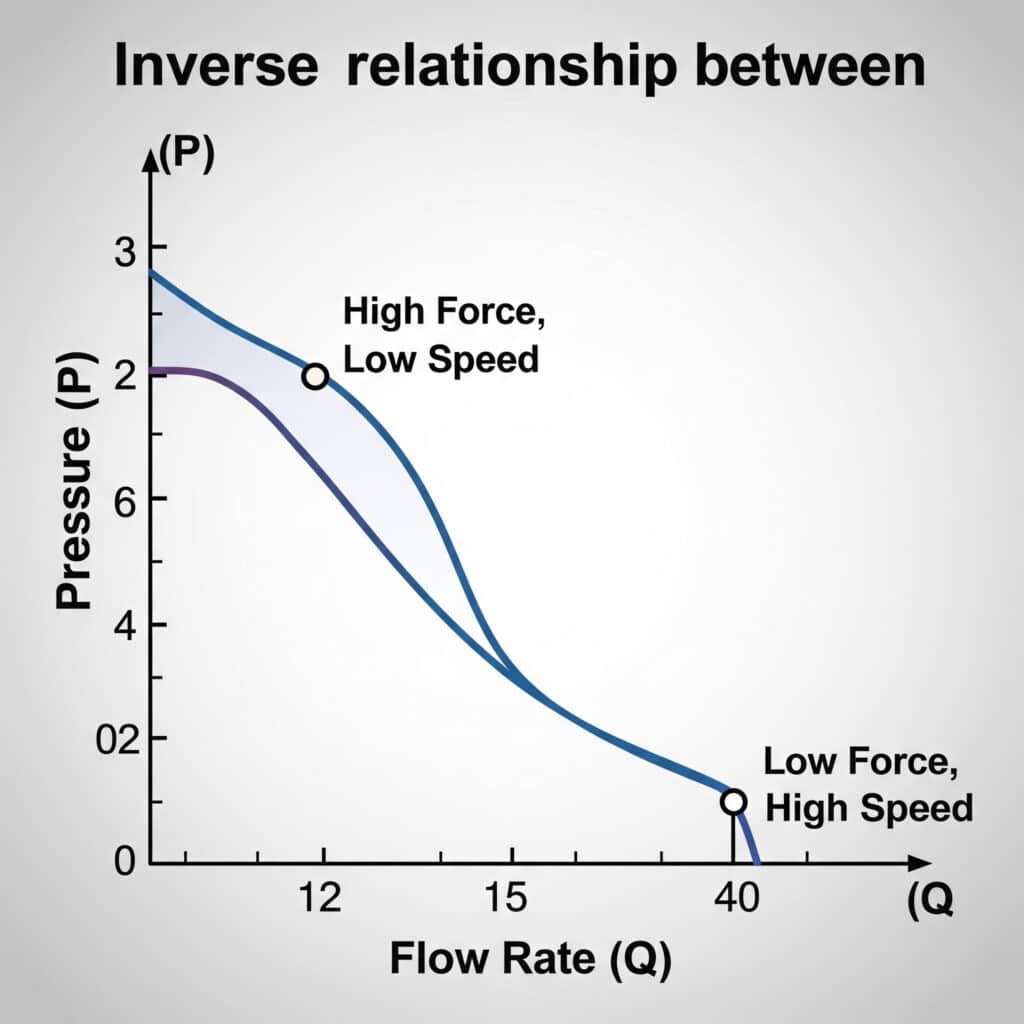
Áramlás-nyomás átváltási táblázat
Ez a praktikus referenciatáblázat az áramlási sebesség és a különböző rendszerelemeken fellépő nyomásesés közötti kapcsolatot mutatja be:
| Csőméret (mm) | Áramlási sebesség (l/min) | Nyomáscsökkenés (bar/méter) 6 bar tápegységnél |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
Az áramlás és a nyomás matematikája
Az áramlás és a nyomás közötti kapcsolat több gáztörvényt követ:
Poiseuille-egyenlet3 lamináris áramlás esetén
Lamináris áramláshoz csöveken keresztül:
Q = (π × r⁴ × ΔP) / (8 × η × L)
Hol:
- Q = térfogatáram
- r = a cső sugara
- ΔP = nyomáskülönbség
- η = dinamikus viszkozitás
- L = A cső hossza
Áramlási együttható (Cv)4 Módszer
Az olyan alkatrészekhez, mint a szelepek:
Q = Cv × √ΔP
Hol:
- Q = Áramlási sebesség
- Cv = Áramlási együttható
- ΔP = nyomásesés az alkatrészen
Henger fordulatszám számítása
A pneumatikus henger sebessége az áramlási sebességtől és a henger felületétől függ:
v = Q / A
Hol:
- v = a henger sebessége (m/s)
- Q = Áramlási sebesség (m³/s)
- A = dugattyú területe (m²)
Egy nemrégiben egy franciaországi csomagolóüzemben végzett projekt során találkoztam egy olyan helyzettel, amikor az ügyfél rúd nélküli hengerei a megfelelő nyomás ellenére túl lassan mozogtak. Az áramlás-nyomás számításaink segítségével elemezve a rendszerüket, azonosítottuk a jelentős nyomásesést okozó, alulméretezett tápvezetékeket. A 6 mm-es csövekről 10 mm-esre történő frissítés után a ciklusidő 40%-vel javult, ami drámaian megnövelte a termelési kapacitást.
Kritikus áramlási megfontolások
A pneumatikus rendszerek áramlás-nyomás viszonyát több tényező befolyásolja:
Fojtott áramlási jelenség5
Ha a nyomásarány meghalad egy kritikus értéket (levegő esetében körülbelül 0,53), az áramlás "fojtottá" válik, és nem tud növekedni, függetlenül a nyomáscsökkentéstől.
Hőmérsékleti hatások
Az áramlási sebességet a hőmérséklet a következő összefüggés szerint befolyásolja:
Q₂ = Q₁ × √(T₂/T₁)
Hol:
- Q₁, Q₂ = Áramlási sebességek különböző hőmérsékleteken
- T₁, T₂ = abszolút hőmérsékletek
Miért kritikus a nyomásegységek átváltásának megértése a rendszertervezéshez?
A világszerte használt különböző nyomásegységek ismerete elengedhetetlen a megfelelő rendszertervezéshez és a nemzetközi kompatibilitáshoz.
A nyomásegységek átváltása kritikus fontosságú, mivel a pneumatikus alkatrészek és specifikációk régiótól és iparágtól függően különböző egységeket használnak. Az egységek helytelen értelmezése jelentős számítási hibákhoz vezethet, amelyek potenciálisan veszélyes következményekkel járhatnak. Az abszolút, a mérő- és a differenciálnyomás közötti átváltás további összetettséget jelent.
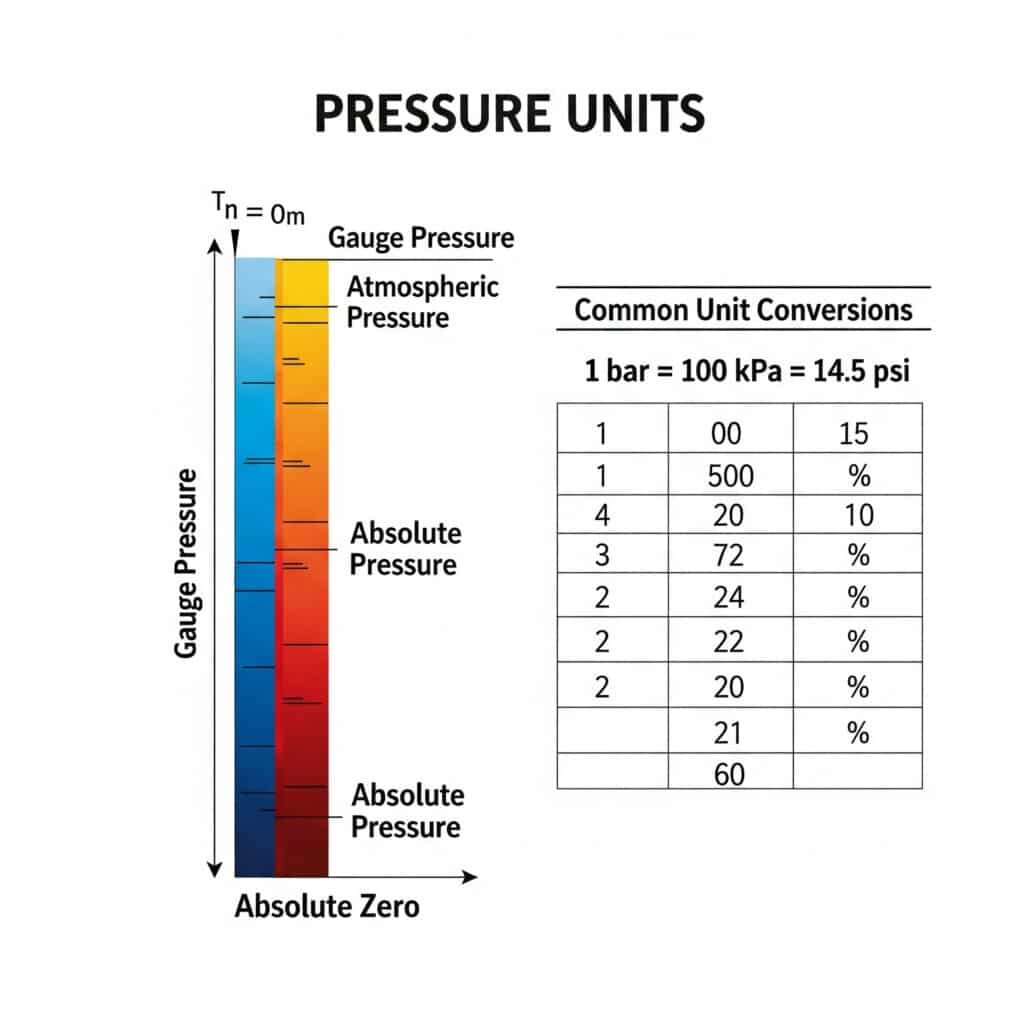
Abszolút nyomás egység átváltási útmutató
Ez az átfogó átváltási táblázat segít eligazodni a világszerte használt különböző nyomásegységekben:
| Egység | Szimbólum | Egyenértékű Pa-ban | Egyenérték barban | Egyenérték psi-ben |
|---|---|---|---|---|
| Pascal | Pa | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| Bar | bár | 1 × 10⁵ | 1 | 14.5038 |
| Font per négyzetcentiméter | psi | 6,894.76 | 0.0689476 | 1 |
| Kilogramm-erő négyzetcentiméterenként | kgf/cm² | 98,066.5 | 0.980665 | 14.2233 |
| Megapascal | MPa | 1 × 10⁶ | 10 | 145.038 |
| Atmoszféra | atm | 101,325 | 1.01325 | 14.6959 |
| Torr | Torr | 133.322 | 0.00133322 | 0.0193368 |
| Milliméter higany | mmHg | 133.322 | 0.00133322 | 0.0193368 |
| Egy hüvelyk víz | inH₂O | 249.089 | 0.00249089 | 0.0361274 |
Abszolút vs. mérőnyomás
Az abszolút és a mérőnyomás közötti különbség megértése alapvető fontosságú:
Nyomás átváltási kalkulátor
Nyomás egység konverter
Henger áramlási sebesség átalakító
Átváltási képletek
- P_abszolút = P_nagyság + P_atmoszférikus
- P_gauge = P_abszolút - P_atmoszférikus
Ahol a szabványos légköri nyomás kb:
- 1,01325 bar
- 14,7 psi
- 101,325 Pa
Egyszer egy németországi mérnöki csapattal dolgoztam együtt, akik megvásárolták a rúd nélküli hengereket, de jelentették, hogy nem érik el a várt erőt. Némi hibaelhárítás után rájöttünk, hogy az erő táblázatainkat használták (amelyek a mérőnyomáson alapultak), de abszolút nyomásértékeket adtak meg. Ez az egyszerű félreértés 1 bar téves számítást okozott az erőelvárásaikban. A nyomásreferencia tisztázása után a rendszerük pontosan a specifikációnak megfelelően működött.
Gyakorlati átalakítási példák
Vegyünk végig néhány gyakori konverziós forgatókönyvet:
Példa 1: Az üzemi nyomás átváltása az egységek között
0,7 MPa maximális üzemi nyomásra méretezett palack:
A bárban:
0,7 MPa × 10 bar/MPa = 7 bar
Psiben:
0,7 MPa × 145,038 psi/MPa = 101,5 psi
Példa 2: Átváltás mérőnyomásról abszolút nyomásra
6 bar nyomáson működő rendszer:
Abszolút nyomás (bar):
6 bar_gauge + 1,01325 bar_atmoszférikus = 7,01325 bar_abszolút
Példa 3: Átváltás kgf/cm²-ről MPa-ra
Egy japán henger, amelyet 7 kgf/cm²-re határoztak meg:
MPa-ban:
7 kgf/cm² × 0,0980665 MPa/(kgf/cm²) = 0,686 MPa
Regionális nyomásegység preferenciák
A különböző régiók jellemzően különböző nyomásegységeket használnak:
| Régió | Közös nyomásegységek |
|---|---|
| Észak-Amerika | psi, inHg, inH₂O |
| Európa | bar, Pa, mbar |
| Japán | kgf/cm², MPa |
| Kína | MPa, bar |
| UK | bar, psi, Pa |
Nyomásmérés a dokumentációban
A nyomási előírások dokumentálásakor fontos, hogy egyértelműen jelezzük:
- A számérték
- A mértékegység
- Legyen szó mérőnyomásról (g) vagy abszolút (a) nyomásról.
Például:
- 6 bar_g (nyomás, 6 bar a légköri nyomás felett)
- 7,01 bar_a (abszolút nyomás, teljes nyomás, beleértve a légköri nyomást is)
Következtetés
A pneumatikus hengerek mögötti fizika megértése - a Pascal-törvény erőszámításaitól az áramlás-nyomás összefüggésekig és a nyomásegységek átváltásáig - elengedhetetlen a megfelelő rendszertervezéshez és hibaelhárításhoz. Ezek az alapelvek segítenek biztosítani, hogy a pneumatikus rendszerek megbízhatóan és hatékonyan nyújtsák az elvárt teljesítményt.
GYIK a pneumatikus rendszerek fizikájáról
Hogyan számolhatom ki egy rúd nélküli pneumatikus henger kimeneti erejét?
A rúd nélküli pneumatikus henger kimenő erejének kiszámításához szorozza meg az üzemi nyomást a dugattyú effektív felületével (F = P × A). Például egy 50 mm-es furatú (0,001963 m² felületű), 6 bar (600 000 Pa) nyomáson működő rúd nélküli henger körülbelül 1178 N erő kifejtésére képes. A hagyományos hengerekkel ellentétben a rúd nélküli hengerek jellemzően mindkét irányban azonos hasznos területtel rendelkeznek.
Hogyan számolhatom ki egy rúd nélküli pneumatikus henger kimeneti erejét?
A rúd nélküli pneumatikus henger kimenő erejének kiszámításához szorozza meg az üzemi nyomást a dugattyú effektív felületével (F = P × A). Például egy 50 mm-es furatú (0,001963 m² felületű), 6 bar (600 000 Pa) nyomáson működő rúd nélküli henger körülbelül 1178 N erő kifejtésére képes. A hagyományos hengerekkel ellentétben a rúd nélküli hengerek jellemzően mindkét irányban azonos hasznos területtel rendelkeznek.
Mi a különbség a mérőnyomás és az abszolút nyomás között?
A nyomás (bar_g, psi_g) a légköri nyomáshoz viszonyított nyomást méri, a légköri nyomás nulla. Az abszolút nyomás (bar_a, psi_a) a tökéletes vákuumhoz viszonyított nyomást méri, amely nulla. A mérőnyomásról abszolút nyomásra történő átváltáshoz a mérőálláshoz hozzá kell adni a légköri nyomást (kb. 1,01325 bar vagy 14,7 psi).
Hogyan befolyásolja a légáramlás a hengerek fordulatszámát?
A henger sebessége egyenesen arányos a levegő áramlási sebességével és fordítottan arányos a dugattyú felületével (v = Q/A). Az alulméretezett tápvezetékek, szűkítő szerelvények vagy nem megfelelő szelepek miatt nem megfelelő áramlási sebesség a nyomástól függetlenül korlátozza a henger sebességét. Például egy 0,002 m² dugattyúfelülettel rendelkező hengeren keresztül történő 20 liter/másodperc áramlási sebesség 10 méter/másodperc sebességet eredményez.
Miért mozognak a pneumatikus hengerek néha lassabban a számítottnál?
A pneumatikus hengerek a számítottnál lassabban mozoghatnak több tényező miatt: nyomásesést okozó levegőellátási korlátozások, a tömítésekből eredő belső súrlódás, a számításokat meghaladó mechanikai terhelések, az effektív nyomást csökkentő szivárgás vagy a hőmérsékletnek a levegő sűrűségére gyakorolt hatása miatt. Ezenkívül a szelepek áramlási együtthatói gyakran korlátozzák a henger számára rendelkezésre álló tényleges áramlási sebességet.
Hogyan konvertálhatok a különböző nyomásegységek között a nemzetközi specifikációkhoz?
A nyomásegységek közötti átváltáshoz használjon szorzótényezőket: 1 bar = 100 000 Pa = 0,1 MPa = 14,5038 psi = 1,01972 kgf/cm². Mindig ellenőrizze, hogy a nyomás mértékegységként vagy abszolút értékként van-e megadva, mivel ez a megkülönböztetés jelentősen befolyásolhatja a számításokat. Például 6 bar_g 7,01325 bar_a értéknek felel meg normál légköri körülmények között.
Mi a kapcsolat a hengerfurat mérete és a leadott erő között?
A henger furatmérete és a leadott erő közötti kapcsolat kvadratikus - a furat átmérőjének megduplázása négyszeresére növeli a leadott erőt (mivel a terület = π × r²). Például 6 bar üzemi nyomáson egy 40 mm-es furatú henger körülbelül 754 N erőt termel, míg egy 80 mm-es furatú henger körülbelül 3 016 N-t, azaz közel négyszer nagyobb erőt.
-
Részletesen elmagyarázza a Pascal-törvényt, a folyadékmechanika egyik alapelvét, amely a hidraulikus és pneumatikus erőátvitel alapja. ↩
-
Világos meghatározást és összehasonlítást nyújt a mérőnyomás és az abszolút nyomás között, ami a pontos mérnöki számítások szempontjából kritikus fontosságú megkülönböztetés, mivel a mérőnyomás a légköri nyomáshoz viszonyítva van. ↩
-
Ismerteti a Poiseuille-törvény levezetését és alkalmazását, amely leírja egy hosszú hengeres csőben lamináris rendszerben áramló inkompresszibilis és newtoni folyadék nyomásesését. ↩
-
Megadja az áramlási együttható (Cv) műszaki meghatározását, amely egy olyan angolszász mértékegység, amely szabványosított módot biztosít a különböző szelepek áramlási kapacitásának összehasonlítására. ↩
-
Részletesen ismerteti a fojtott áramlás fizikáját, amely egy áramlástani feltétel, amely korlátozza egy összenyomható folyadék tömegáramlását egy korláton keresztül, amikor a sebesség eléri a hangsebességet. ↩



