A helytelen dugattyúterület-számítások a pneumatikus rendszer 40% alulteljesítményének problémáit okozzák, ami elégtelen erőkifejtéshez, lassú ciklusidőkhöz és költséges túlméretezett berendezések beszerzéséhez vezet. A dugattyú effektív területe a kettős működésű hengerekben egyenlő a teljes furatfelülettel kihúzáskor és a furatfelület mínusz a rúdfelület behúzáskor, a számításokhoz pontos átmérőmérésekre és a nyomáskülönbségek figyelembevételére van szükség a pontos erő előrejelzéséhez. Tegnap segítettem Davidnek, egy kaliforniai mérnöknek, akinek az automatizált összeszerelő sora 30% lassabban futott a tervezettnél, mert rosszul számolta ki a dugattyúk területét és alulméretezte a levegőellátó rendszerét. 📐
Tartalomjegyzék
- Mi a dugattyú effektív területe és miért fontos a henger teljesítménye szempontjából?
- Hogyan számolja ki a dugattyú területét a kinyújtási és behúzási lökésekhez?
- Milyen tényezők befolyásolják a dugattyúterület számítását valós alkalmazásokban?
Mi a dugattyú effektív területe és miért fontos a henger teljesítménye szempontjából?
A hatékony dugattyúterület megértése alapvető fontosságú a megfelelő pneumatikus rendszer tervezéséhez és a teljesítmény optimalizálásához.
A dugattyú effektív felülete a dugattyú tényleges felülete, amelyre a légnyomás hat, hogy erőt fejtsen ki, ami a dugattyú egyik oldalán lévő rúd által elfoglalt hely miatt különbözik a kitolási és behúzási lökések között.
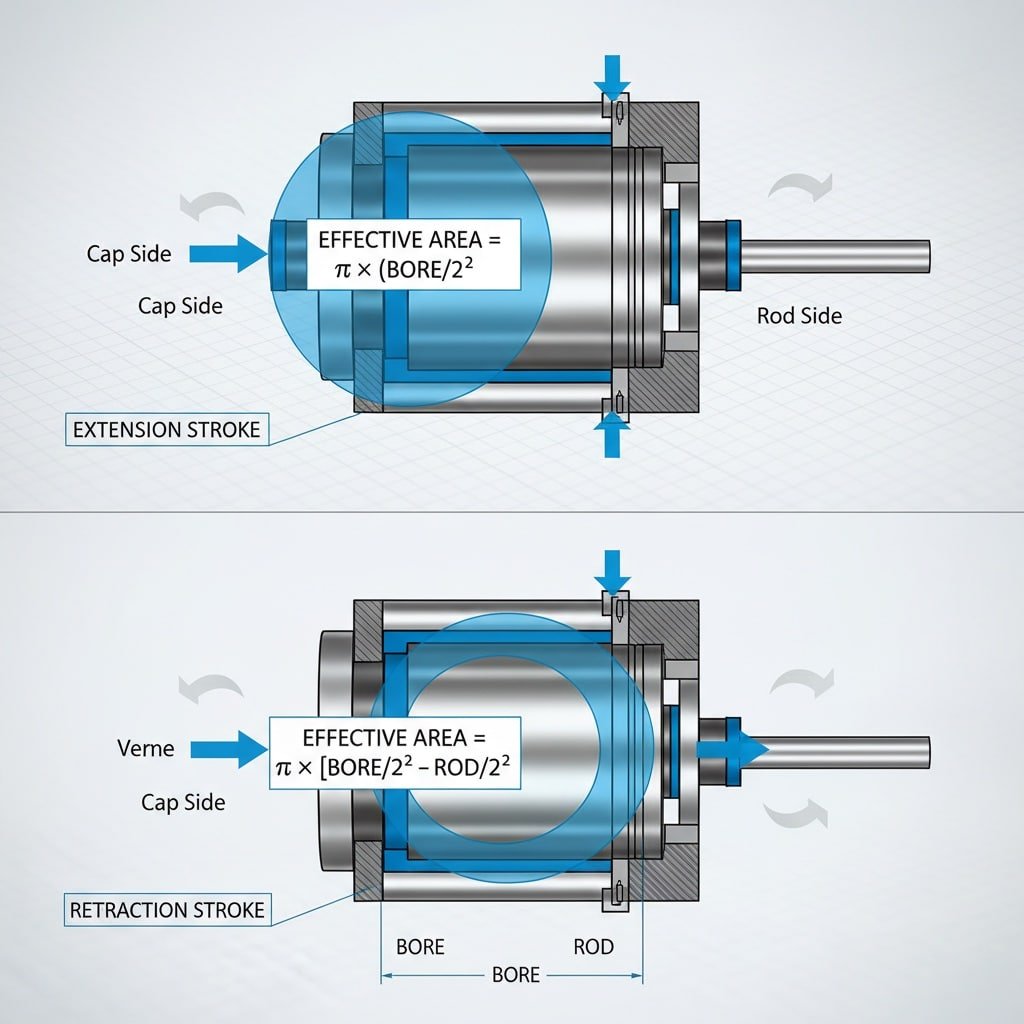
Alapvető dugattyúterületi fogalmak
Hosszabbító löket (rúd kihúzása):
- A teljes furat területe kapja a légnyomást
- Maximális erőkifejtési képesség
- Rúdoldali szellőzőnyílások a légkörbe vagy a visszatérő nyílásba
- Terület = π × (furatátmérő/2)²1
Visszahúzási löket (rúd visszahúzása):
- A rúd elmozdulása miatt csökkent effektív felület
- Alacsonyabb erőkifejtés a hosszabbításhoz képest
- A sapka oldala szellőzik, míg a rúd oldala kapja a nyomást
- Terület = π × [(furatátmérő/2)² - (rúdátmérő/2)²]
Teljesítmény hatása
| Henger mérete | Bővítési terület | Visszahúzási terület | Erő arány |
|---|---|---|---|
| 2″ furat, 1″ rúd | 3,14 in² | 2,36 in² | 1.33:1 |
| 4″ furat, 1,5″ rúd | 12,57 in² | 10,81 in² | 1.16:1 |
| 6″ furat, 2″ rúd | 28,27 in² | 25,13 in² | 1.12:1 |
Miért fontosak a pontos számítások
Rendszertervezési következmények:
- A kimenő erő közvetlenül arányos a hatásos területtel
- A levegőfogyasztás a dugattyú területével változik
- A ciklusidő függ a terület-mennyiség aránytól
- A nyomásigény a területkülönbségekkel együtt skálázódik
Költségek:
- A túlméretezett rendszerek energiát pazarolnak és növelik a költségeket
- Az alulméretezett rendszerek nem felelnek meg a teljesítménykövetelményeknek
- A megfelelő méretezés optimalizálja a berendezés beruházását
- A pontos számítások megelőzik a drága újratervezéseket
Dávid futószalagja tökéletesen illusztrálja ezt. Az eredeti számításai mindkét löketnél a teljes furatfelületet használták, ami a behúzóerő 25% túlbecsléséhez vezetett. Ez azt eredményezte, hogy alulméretezte a levegőellátást, ami lassú behúzási sebességet eredményezett, ami az egész gyártósor szűk keresztmetszetét okozta. Újraszámoltuk a megfelelő hatásos területek felhasználásával, és ennek megfelelően korszerűsítettük a légrendszert, visszaállítva a teljes tervezési teljesítményt. 🎯
Hogyan számolja ki a dugattyú területét a kinyújtási és behúzási lökésekhez?
A pontos matematikai képletek biztosítják a pontos erő- és teljesítmény-előrejelzéseket a kettős működésű pneumatikus hengerek esetében.
A kihúzási terület egyenlő π × (D/2)², ahol D a furat átmérője, míg a behúzási terület egyenlő π × [(D/2)² - (d/2)²], ahol d a rúd átmérője, a pontos eredmények érdekében minden mérés egységes mértékegységben történik.
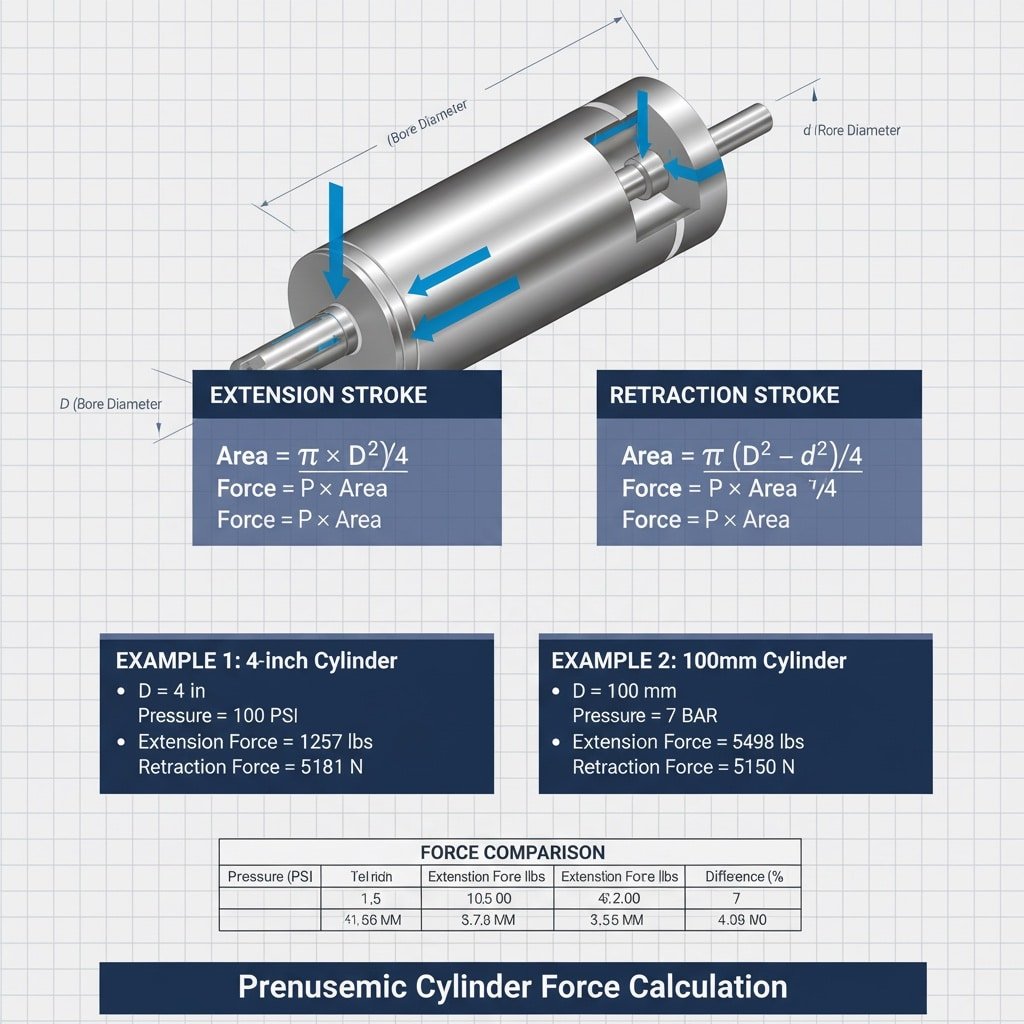
Lépésről lépésre történő számítási folyamat
Szükséges méretek:
- Hengerfurat átmérője (D)
- Rúdátmérő (d)
- Üzemi nyomás (P)
- Biztonsági tényező2 követelmények
Bővítési terület képlete:
- A_kiterjesztés = π × (D/2)²
- A_kiterjesztés = π × D²/4
- A_extension = 0,7854 × D²
Visszahúzási terület képlete:
- A_visszahúzás = π × [(D/2)² - (d/2)²]
- A_visszahúzás = π × (D² - d²)/4
- A_visszahúzódás = 0,7854 × (D² - d²)
Gyakorlati számítási példák
Példa 1: Szabványos 4 hüvelykes henger
- Furatátmérő: 4,0 hüvelyk
- Rúd átmérő: 1,5 hüvelyk
- Bővítési terület: 0,7854 × 4² = 12,57 in²
- Visszahúzódó terület: (4² - 1,5²) = 10,81 in².
Példa 2: 100 mm-es metrikus henger
- Furatátmérő: 100mm
- Rúd átmérő: 25mm
- Bővítési terület: = 7,854 mm².
- Visszahúzódó terület: (100² - 25²) = 7,363 mm².
Erőszámítási alkalmazások
| Nyomás (PSI) | Hosszabbító erő (lbs) | Visszahúzó erő (font) | Erő különbség |
|---|---|---|---|
| 60 PSI | 754 font | 649 font | 14% csökkentés |
| 80 PSI | 1,006 font | 865 font | 14% csökkentés |
| 100 PSI | 1,257 font | 1,081 font | 14% csökkentés |
Haladó szempontok
Nyomáscsökkenés3 Hatások:
- A vezetékveszteségek csökkentik az effektív nyomást
- Az áramláskorlátozások befolyásolják a dinamikus teljesítményt
- A szelepnyomás csökkenése befolyásolja a tényleges erőt
- A hőmérséklet-változások befolyásolják a nyomást
Biztonsági tényező integrálása:
- A számított erőkre 1,5-2,0 biztonsági tényezőt kell alkalmazni.
- Vegyük figyelembe a dinamikus terhelési feltételeket
- A kopás és a teljesítménycsökkenés figyelembevétele
- Környezeti tényező kiigazítások beépítése
Maria, egy oregoni géptervező, következetlen szorítóerőt tapasztalt a csomagolóberendezésében. A számításai helyesnek tűntek, de nem számolt a szeleprendszeren keresztül fellépő 15 PSI nyomáseséssel. Segítettünk neki újraszámolni az effektív nyomást, és ennek megfelelően átméretezni a hengereket, így az egész gyártósoron következetes ±2% erőismétlést ért el. 💪
Milyen tényezők befolyásolják a dugattyúterület számítását valós alkalmazásokban?
A valós alkalmazások olyan változókat vezetnek be, amelyek jelentősen befolyásolják a dugattyúterület hatékony teljesítményét, és amelyeket figyelembe kell venni a pontos rendszertervezéshez.
A gyártási tűrések, a tömítés súrlódása, a nyomásveszteségek, a hőmérsékleti hatások és a dinamikus terhelési körülmények mind befolyásolják a dugattyú tényleges hatékony teljesítményét, ami a rendszer megbízható működéséhez az elméleti számítások mérnöki kiigazítását igényli.
Gyártási tolerancia hatása
Méretváltozatok:
- Furatátmérő tűrés: jellemzően ±0,002″.
- Rúdátmérő tűrés: jellemzően ±0,001″
- A felületkezelés hatása a tömítésre
- Szerelési távolsági követelmények
Tolerancia hatáselemzés:
- 0,002″ furatváltozás = ±0,6% területváltozás
- A kombinált tűrések ±1,2% erőeltérést eredményezhetnek
- A minőségellenőrzés biztosítja az egyenletes teljesítményt
- A Bepto fenntartja a ±0,001″ tűrési szabványokat
Környezeti tényezők
Hőmérsékleti hatások:
- Hőtágulás4 megváltoztatja a méreteket
- Tömítőanyag hőmérsékleti együtthatók
- A levegő sűrűségének változása a hőmérséklet függvényében
- A kenés viszkozitásának változása
Nyomásrendszer-változók:
- Nyomásszabályozási pontosság
- Vezetéknyomás csökkenés működés közben
- Szelep áramlási jellemzői
- A légkezelő rendszer teljesítménye
Dinamikus teljesítményre vonatkozó megfontolások
| Működési feltétel | Területi hatékonyság | Teljesítmény hatása |
|---|---|---|
| Statikus tartás | 100% | Teljes névleges erő |
| Lassú mozgás | 95-98% | Súrlódási veszteségek |
| Nagy sebességű működés | 85-92% | Áramláskorlátozások |
| Piszkos körülmények | 80-90% | Fokozott súrlódás |
Bepto Engineering előnyei
Precíziós gyártás:
- Az ipari szabványoknál szigorúbb tűrések
- A továbbfejlesztett felületi felületek csökkentik a súrlódást
- A prémium tömítőanyagok minimalizálják a veszteségeket
- Átfogó minőségvizsgálati protokollok
Teljesítményoptimalizálás:
- Egyedi területszámítások egyedi alkalmazásokhoz
- Környezeti tényezőelemzés és kompenzáció
- Dinamikus teljesítménymodellezés és validálás
- Folyamatos támogatás a rendszer optimalizálásához
Valós világbeli validálás:
- A helyszíni tesztelés megerősíti az elméleti számításokat
- A teljesítményfigyelés azonosítja az optimalizálási lehetőségeket
- Folyamatos fejlesztés az alkalmazás visszajelzései alapján
- Műszaki támogatás a hibaelhárításhoz és frissítésekhez
Precíziós gyártásunk és mérnöki támogatásunk segítségével ügyfeleink 98%+ elméleti teljesítményt érnek el valós alkalmazásokban, szemben a szabványos alkatrészeknél jellemző 85-90%-vel. Teljes körű számítási szolgáltatásokat, alkalmazáselemzést és teljesítményhitelesítést biztosítunk, hogy pneumatikus rendszerei pontosan azt a teljesítményt nyújtsák, amire szüksége van. 🔧
Következtetés
A pontos hatásos dugattyúfelület-számítások elengedhetetlenek a megfelelő pneumatikus rendszer tervezéséhez, biztosítva az optimális teljesítményt, hatékonyságot és költséghatékonyságot a kettős működésű hengerek alkalmazásainál.
GYIK az effektív dugattyúterület számításairól
K: Miért kisebb a behúzóerő mindig, mint a kinyújtóerő a kettős működésű hengereknél?
A visszahúzó erő kisebb, mivel a rúd a nyomásoldalon helyet foglal, és a rúd keresztmetszetével csökkenti a dugattyú effektív felületét. Ez jellemzően 10-30% kisebb erőt eredményez a rúd és a furat arányától függően.
K: Hogyan befolyásolják a gyártási tűrések a dugattyúterület számításait?
A gyártási tűrések ±1-2% eltérést okozhatnak a tényleges dugattyúfelületben, ami arányosan befolyásolja a leadott erőt. A Bepto a szabványos alkatrészekhez képest (±0,002-0,005″) szigorúbb tűréseket tart fenn (±0,001″) a következetesebb teljesítmény érdekében.
K: Milyen biztonsági tényezőket kell alkalmazni a számított dugattyúterületekhez?
Alkalmazzon 1,5-2,0 biztonsági tényezőt a nyomásveszteségek, a tömítés súrlódása és a teljesítmény idővel történő romlása miatt. Kritikus alkalmazásoknál a kockázatértékelés és a szabályozási követelmények alapján magasabb biztonsági tényezőkre lehet szükség.
K: Hogyan befolyásolják a nyomásesések a dugattyú hatékony teljesítményét?
A nyomásesés nem változtatja meg a dugattyú fizikai felületét, de csökkenti az effektív nyomást, ezzel arányosan csökkentve a leadott erőt. Egy 10 PSI nyomáscsökkenés 80 PSI üzemi nyomáson 12,5%-vel csökkenti az erőt, ami nagyobb hengereket vagy nagyobb tápfeszültségi nyomást igényel.
K: Tud a Bepto egyedi dugattyúfelület-számításokat végezni az adott alkalmazásomhoz?
Igen, mérnöki csapatunk ingyenes dugattyúterület-számításokat, erőelemzést és rendszer méretezési ajánlásokat biztosít bármilyen alkalmazáshoz. Az optimális teljesítmény és megbízhatóság biztosítása érdekében figyelembe vesszük az összes valós tényezőt.
-
Tekintse át a kör területének kiszámítására szolgáló alapvető képletet. ↩
-
Ismerje meg a biztonsági tényezők szerepét a gépészeti tervezésben, és hogy miért kritikusak. ↩
-
Értse a nyomásesés okait a pneumatikus rendszerekben, és hogy ez hogyan befolyásolja a teljesítményt. ↩
-
Fedezze fel a hőtágulás elvét és annak hatásait a mechanikai alkatrészekre. ↩



