A mérnökök a pneumatikus hengerrendszerek tervezésekor gyakran tévesen számítják ki a rúdterületeket, ami helytelen erőszámításokhoz és a rendszer teljesítményének meghibásodásához vezet.
A rúd területe a kör keresztmetszetű terület, amely A = πr² vagy A = π(d/2)², ahol "r" a rúd sugara és "d" a rúd átmérője, ami kritikus az erő- és nyomásszámítások szempontjából.
Tegnap segítettem Carlosnak, egy mexikói tervezőmérnöknek, akinek a pneumatikus rendszere meghibásodott, mert elfelejtette kivonni a rúd területét a dugattyú területéből a kettős működésű henger erőszámításai során.
Tartalomjegyzék
- Mi a rúdterület a pneumatikus hengerrendszerekben?
- Hogyan számolja ki a rúd keresztmetszeti területét?
- Miért fontos a rúd területe az erőszámításoknál?
- Hogyan befolyásolja a rúd területe a henger teljesítményét?
Mi a rúdterület a pneumatikus hengerrendszerekben?
A rúd területe a dugattyúrúd kör keresztmetszeti területét jelöli, ami elengedhetetlen a hatékony dugattyúfelület és a kettős működésű pneumatikus hengereknél kifejtett erő kiszámításához.
A rúd területe a dugattyúrúd keresztmetszete által elfoglalt, a rúd tengelyére merőlegesen mért kör alakú terület, amelyet az erőszámításokhoz használt nettó effektív területek meghatározására használnak.
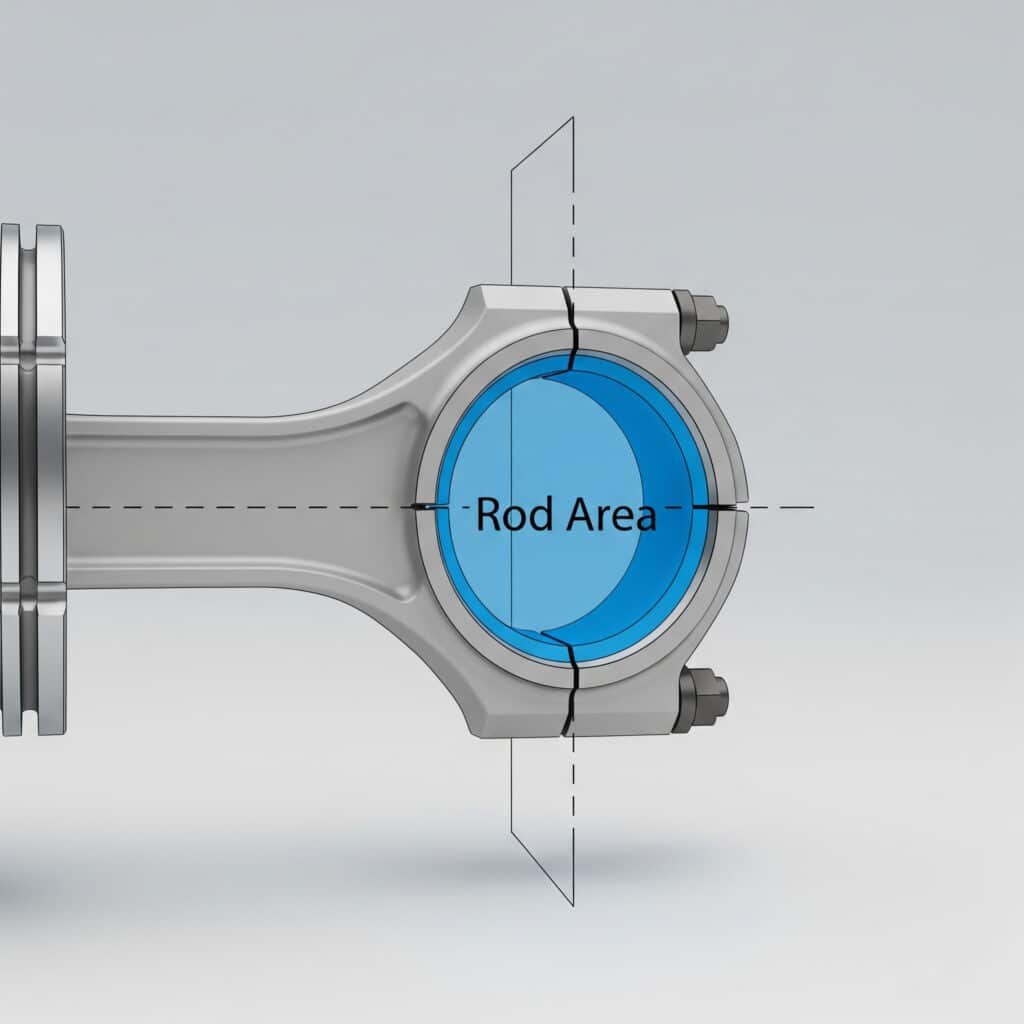
Rúdterület meghatározása
Geometriai tulajdonságok
- Kör keresztmetszet: Szabványos rúdgeometria
- Merőleges mérés: 90° a rúd középvonalához képest
- Állandó terület: Egyenletes a rúd hossza mentén
- Szilárd terület: Teljes anyagi keresztmetszet
Főbb mérések
- Rúd átmérő: Elsődleges dimenzió a terület kiszámításához
- Rúd sugara: Az átmérő mérés fele
- Keresztmetszeti terület: Kör alakú terület képlet alkalmazása
- Hatékony terület: Hatás a henger teljesítményére
Rúd és dugattyú területének viszonya
| Komponens | Terület képlet | Cél | Alkalmazás |
|---|---|---|---|
| Dugattyú | A = π(D/2)² | Teljes furat területe | Erőszámítás kiterjesztése |
| Rod | A = π(d/2)² | Rúd keresztmetszete | Behúzási erő számítása |
| Nettó terület | A_dugattyú - A_rúd | Hatékony behúzási terület | Dupla működtetésű hengerek |
| Gyűrűs terület1 | π(D² - d²)/4 | Gyűrű alakú terület | Rúdoldali nyomás |
Szabványos rúdméretek
Gyakori rúdátmérők
- 8 mm-es rúd: Terület = 50,3 mm²
- 12 mm-es rúd: Terület = 113,1 mm²
- 16 mm-es rúd: Terület = 201,1 mm²
- 20mm-es rúd: Terület = 314,2 mm²
- 25 mm-es rúd: Terület = 490,9 mm²
- 32 mm-es rúd: Terület = 804,2 mm²
Rúd-búrához viszonyított arányok
- Normál arány: Rúdátmérő = 0,5 × furatátmérő
- Nehéz teher: Rúdátmérő = 0,6 × furatátmérő
- Könnyű teher: Rúdátmérő = 0,4 × furatátmérő
- Egyedi alkalmazások: Igény szerint változik
Rúdterületi alkalmazások
Erő számítások
A rúd területét használom:
- Erő kiterjesztése: Teljes dugattyúfelület × nyomás
- Visszahúzó erő: (dugattyú területe - rúd területe) × nyomás
- Erőkülönbség: Különbség a kiterjesztés/visszahúzás között
- Terheléselemzés: A henger illesztése az alkalmazáshoz
Rendszertervezés
A rúd területét érinti:
- Henger kiválasztása: Az alkalmazások megfelelő méretezése
- Sebesség számítások: Áramlási követelmények irányonként
- Nyomási követelmények: Rendszernyomás-specifikációk
- Teljesítmény optimalizálás: Kiegyensúlyozott működés kialakítása
Rúdterület a különböző henger típusokban
Egyszeres működésű hengerek
- Nincs rúdterületre gyakorolt hatás: Tavaszi visszatérés
- Csak az erő kiterjesztése: Teljes dugattyúterület hatékony
- Egyszerűsített számítások: Nincs visszahúzóerő figyelembevétele
- Költségoptimalizálás: Csökkentett összetettség
Dupla működtetésű hengerek
- Rúdterület kritikus: Befolyásolja a behúzási erőt
- Aszimmetrikus működés: Különböző erők minden irányban
- Komplex számítások: Mindkét területet figyelembe kell venni
- Teljesítménykiegyenlítés: Szükséges tervezési megfontolások
Rúd nélküli hengerek
- Nincs rúdterület: A tervezésből kiiktatva
- Szimmetrikus művelet: Egyenlő erők mindkét irányban
- Egyszerűsített számítások: Egyetlen terület figyelembevétele
- Térbeli előnyök: Nincs szükség rúdhosszabbításra
Hogyan számolja ki a rúd keresztmetszeti területét?
A rúd keresztmetszeti területének kiszámítása a szabványos kör alakú terület képletét használja a rúd átmérőjének vagy sugarának mérésével a pontos pneumatikus rendszertervezéshez.
Számítsuk ki a rúd területét A = πr² (sugárral) vagy A = π(d/2)² (átmérővel) segítségével, ahol π = 3,14159, biztosítva a számítás során a következetes mértékegységeket.
Alapvető terület képlet
A rúd sugara használata
A = πr²
- A: Rúd keresztmetszeti területe
- π: 3.14159 (matematikai állandó)
- r: Rúd sugara (átmérő ÷ 2)
- Egységek: Terület négyzetmértékben, sugárban kifejezve
Rúdátmérő használata
A = π(d/2)² vagy A = πd²/4
- A: Rúd keresztmetszeti területe
- π: 3.14159
- d: Rúdátmérő
- Egységek: Terület átmérő egységekben kifejezve négyzetben
Lépésről lépésre történő számítás
Mérési folyamat
- Rúdátmérő mérése: A pontosság érdekében használjon mérőszöget
- Mérés ellenőrzése: Vegyen többszörös leolvasást
- Sugár kiszámítása: r = átmérő ÷ 2 (ha a sugár képletet használjuk)
- Alkalmazza a képletet: A = πr² vagy A = π(d/2)²
- Ellenőrizze az egységeket: Egységes egységrendszer biztosítása
Számítási példa
20 mm átmérőjű rúdhoz:
- 1. módszer: A = π(10)² = π × 100 = 314,16 mm².
- 2. módszer: A = π(20)²/4 = π × 400/4 = 314,16 mm².
- Ellenőrzés: Mindkét módszer azonos eredményt ad
Rúdterület számítási táblázat
| Rúd átmérő | Rúd sugara | Terület számítása | Rúd terület |
|---|---|---|---|
| 8mm | 4mm | π × 4² | 50,3 mm² |
| 12mm | 6mm | π × 6² | 113,1 mm² |
| 16mm | 8mm | π × 8² | 201,1 mm² |
| 20mm | 10mm | π × 10² | 314,2 mm² |
| 25mm | 12.5mm | π × 12.5² | 490,9 mm² |
| 32mm | 16mm | π × 16² | 804,2 mm² |
Mérési eszközök
Digitális kalibrátorok
- Pontosság: ±0,02 mm pontosság
- Tartomány: 0-150mm tipikus
- Jellemzők: Digitális kijelző, egység-átalakítás
- Legjobb gyakorlat: Több mérési pont
Mikrométer
- Pontosság: ±0,001 mm pontosság
- Tartomány: Különböző méretekben kapható
- Jellemzők: Ratchet stop, digitális opciók
- Alkalmazások: Nagy pontosságú követelmények
Gyakori számítási hibák
Mérési hibák
- Átmérő vs. sugár: Rossz dimenzió használata a képletben
- Egység inkonzisztencia: mm és hüvelyk keverése
- Precíziós hibák: Nem elegendő tizedesjegy
- Szerszám kalibrálás: Kalibrálatlan mérőműszerek
Képlet hibák
- Rossz képlet: Terület helyett kerület használata
- Hiányzó π: Felejtés matematikai állandó
- Hibák kiegyenlítése: Helytelen exponens alkalmazása
- Egység átváltás: Helytelen egységtranszformációk
Ellenőrzési módszerek
Keresztellenőrzési technikák
- Többszörös számítások: Különböző formulamódszerek
- Mérési hitelesítés: Átmérőmérések megismétlése
- Referenciatáblázatok: Összehasonlítás a standard értékekkel
- CAD szoftver: 3D modell területének számítása
Ésszerűségi ellenőrzések
- Méretbeli korreláció: Nagyobb átmérő = nagyobb terület
- Standard összehasonlítások: Megfelel a tipikus rúdméreteknek
- Alkalmazási alkalmasság: A henger méretének megfelelő
- Gyártási szabványok: Közönséges rendelkezésre álló méretek
Haladó számítások
Üreges rudak
A = π(D² - d²)/4
- D: Külső átmérő
- d: Belső átmérő
- Alkalmazás: Súlycsökkentés, belső útvonalvezetés
- Számítás: A belső területet kivonjuk a külső területből
Nem kör alakú rudak
- Négyszögletes rudak: A = oldal²
- Téglalap alakú rudak: A = hossz × szélesség
- Különleges formák: Megfelelő geometriai képletek használata
- Alkalmazások: Megakadályozza a forgást, különleges követelmények
Amikor Jenniferrel, egy kanadai pneumatikus rendszer tervezőjével dolgoztam, kezdetben helytelenül számította ki a rúd területét, mivel a πr² képletben az átmérőt használta a sugár helyett, ami 4×-es túlbecslést és teljesen rossz erőszámításokat eredményezett a kettős működésű henger alkalmazásánál.
Miért fontos a rúd területe az erőszámításoknál?
A rúdfelület közvetlenül befolyásolja a kettős működésű hengerek rúdoldalán lévő tényleges dugattyúfelületet, ami erőkülönbségeket eredményez a ki- és behúzási műveletek között.
A rúd területe csökkenti a dugattyú effektív felületét behúzáskor, ami a kettős működésű hengereknél a kihúzóerőhöz képest kisebb behúzóerőt eredményez, ami kompenzációt igényel a rendszer tervezésénél.
Erőszámítás alapjai
Alapvető erő képlet
- Erő kiterjesztése: F = P × A_dugattyú
- Visszahúzó erő: F = P × (A_dugattyú - A_rúd)
- Erőkülönbség: Kinyújtóerő > Behúzóerő
- Tervezési hatás: Mindkét irányt figyelembe kell venni
Hatékony területek
- Teljes dugattyúterület: Elérhető a kiterjesztés során
- Nettó dugattyúterület: A dugattyú területe mínusz a rúd területe behúzáskor
- Gyűrűs terület: Gyűrű alakú terület a rúd oldalán
- Terület aránya: Meghatározza az erőkülönbséget
Erőszámítási példák
63mm furat, 20mm rúd henger
- Dugattyú területe: π(31.5)² = 3,117 mm²
- Rúd terület: π(10)² = 314 mm²
- Nettó terület: 3,117 - 314 = 2,803 mm²
- 6 bar nyomáson:
– Erő kiterjesztése: 6 × 3,117 = 18,702 N
– Visszahúzó erő: 6 × 2,803 = 16,818 N
– Erőkülönbség: 1,884 N (10% csökkentés)
Erő összehasonlító táblázat
| Henger mérete | Dugattyú terület | Rúd terület | Nettó terület | Erő arány |
|---|---|---|---|---|
| 32mm/12mm | 804 mm² | 113 mm² | 691 mm² | 86% |
| 50mm/16mm | 1,963 mm² | 201 mm² | 1,762 mm² | 90% |
| 63mm/20mm | 3,117 mm² | 314 mm² | 2,803 mm² | 90% |
| 80mm/25mm | 5,027 mm² | 491 mm² | 4,536 mm² | 90% |
| 100mm/32mm | 7,854 mm² | 804 mm² | 7,050 mm² | 90% |
Alkalmazás hatása
Terhelés-illesztés
- Terhelések kiterjesztése: Teljes névleges erővel képes megbirkózni
- Visszahúzódó terhek: Korlátozza a csökkentett hasznos terület
- Terheléselosztás: Tekintsük az erőkülönbséget a tervezés során
- Biztonsági tartalékok: A csökkentett behúzási képesség figyelembevétele
Rendszer teljesítménye
- Sebességkülönbségek: Irányonként eltérő áramlási követelmények
- Nyomási követelmények: A behúzáshoz nagyobb nyomásra lehet szükség
- Az ellenőrzés összetettsége: Aszimmetrikus műveletre vonatkozó megfontolások
- Energiahatékonyság: Optimalizálás mindkét irányba
Tervezési megfontolások
Rúdméret kiválasztása
- Szabványos arányok: Rúdátmérő = 0,5 × furatátmérő
- Nehéz terhek: Nagyobb rúd a szerkezeti szilárdság érdekében
- Erőegyensúly: Kisebb rúd az egyenlőbb erőkért
- Alkalmazásspecifikus: Egyedi arányok speciális igényekhez
Erőkiegyenlítési stratégiák
- Nyomáskiegyenlítés: Nagyobb nyomás a rúd oldalán
- Területi kompenzáció: Nagyobb henger a behúzási követelményekhez
- Kettős hengerek: Külön hengerek minden irányhoz
- Rúd nélküli kialakítás: A rúd területének hatásainak kiküszöbölése
Gyakorlati alkalmazások
Anyagmozgatás
- Emelési alkalmazások: Erő kiterjesztése kritikus
- Tolóműveletek: Szükség lehet a behúzóerő illesztésére
- Rögzítő rendszerek: Az erőkülönbség befolyásolja a tartási erőt
- Helymeghatározási pontosság: Az erőváltozások befolyásolják a pontosságot
Gyártási folyamatok
- Sajtóműveletek: Következetes erőigény
- Összeszerelő rendszerek: Pontos erőszabályozás szükséges
- Minőségellenőrzés: Az erőváltozások befolyásolják a termék minőségét
- Ciklusidő: Erőkülönbségek ütközési sebesség
Force problémák hibaelhárítása
Gyakori problémák
- Elégtelen behúzóerő: Túl nagy a terhelés a nettó területhez képest
- Egyenetlen működés: Az erőkülönbség problémákat okoz
- Sebességváltozások: Különböző áramlási követelmények
- Ellenőrzési nehézségek: Aszimmetrikus válasz jellemzői
Megoldások
- Henger méretnövelés: Nagyobb furat a megfelelő visszahúzóerő érdekében
- Nyomás beállítása: Optimalizálja a kritikus irányt
- Rúdméret optimalizálás: Egyensúlyi erő vs. erőigény
- A rendszer újratervezése: Fontolja meg a rúd nélküli alternatívákat
Amikor konzultáltam Michaellel, egy ausztráliai gépgyártóval, a csomagolóberendezései következetlenül működtek, mert csak a kinyújtóerőre tervezte őket. A 15% visszahúzóerő-csökkentés elakadást okozott a visszahúzás során, ami a henger méretének növelését tette szükségessé, hogy mindkét irányt megfelelően tudja kezelni.
Hogyan befolyásolja a rúd területe a henger teljesítményét?
A rúd területe jelentősen befolyásolja a henger sebességét, a leadott erőt, az energiafogyasztást és a rendszer általános teljesítményét a pneumatikus alkalmazásokban.
A nagyobb rúdfelületek csökkentik a behúzóerőt és növelik a behúzási sebességet a kisebb hatásos terület és a kisebb légtérfogatigény miatt, aszimmetrikus henger teljesítményjellemzők kialakulásával.
Sebesség Teljesítmény hatása
Áramlási sebesség összefüggések
Sebesség = Áramlási sebesség3 ÷ Hatékony terület
- Sebesség bővítése: Áramlás ÷ teljes dugattyúfelület
- Visszahúzási sebesség: Áramlás ÷ (dugattyú területe - rúd területe)
- Sebességkülönbség: Visszahúzás jellemzően gyorsabb
- Áramlás optimalizálása: Irányonként eltérő követelmények
Sebességszámítási példa
63 mm-es furat, 20 mm-es rúd 100 L/min áramlásnál:
- Sebesség bővítése: 100,000 ÷ 3,117 = 32,1 mm/s
- Visszahúzási sebesség: 100,000 ÷ 2,803 = 35,7 mm/s
- Sebességnövekedés: 11% gyorsabb behúzás
Teljesítményjellemzők
Erő kimeneti hatások
| Rúd mérete | Erőcsökkentés | Sebesség növelése | Teljesítmény hatása |
|---|---|---|---|
| Kicsi (d/D = 0,3) | 9% | 10% | Minimális aszimmetria |
| Standard (d/D = 0,5) | 25% | 33% | Mérsékelt aszimmetria |
| Nagy (d/D = 0,6) | 36% | 56% | Jelentős aszimmetria |
Energiafogyasztás
- A löket meghosszabbítása: Teljes légmennyiség szükséges
- Visszahúzási löket: Csökkentett légtérfogat (rúdkiszorítás)
- Energiamegtakarítás: Alacsonyabb fogyasztás behúzás közben
- A rendszer hatékonysága: Teljes energiaoptimalizálás lehetséges
Levegőfogyasztás elemzése
Térfogatszámítások
- Bővítse a hangerőt: Dugattyú területe × lökethossz
- Visszahúzott hangerő: (dugattyú területe - rúd területe) × lökethossz
- Térfogatkülönbség: Rúd mennyiségi megtakarítás
- Költségek hatása: Csökkentett kompresszorigény
Fogyasztási példa
100 mm-es furat, 32 mm-es rúd, 500 mm-es löket:
- Bővítse a hangerőt: 7,854 × 500 = 3,927,000 mm³
- Visszahúzott hangerő: 7,050 × 500 = 3,525,000 mm³
- Megtakarítás: 402,000 mm³ (10% redukció)
Rendszertervezés optimalizálása
Rúdméret kiválasztási kritériumok
- Szerkezeti követelmények: Hajlítás4 és hajlító terhelések
- Erőegyensúly: Elfogadható erőkülönbség
- Sebességre vonatkozó követelmények: Kívánt sebességi jellemzők
- Energiahatékonyság: Levegőfogyasztás optimalizálása
- Költségekkel kapcsolatos megfontolások: Anyag- és gyártási költségek
Teljesítménykiegyenlítés
- Áramlásszabályozás: Külön szabályozás irányonként
- Nyomáskiegyenlítés: Állítsa be az erőigényt
- Sebességillesztés: Gázpedál gyorsabb irányba, ha szükséges
- Terheléselemzés: A henger illesztése az alkalmazási igényekhez
Alkalmazásspecifikus megfontolások
Nagy sebességű alkalmazások
- Kis rudak: Minimalizálja a sebességkülönbséget
- Áramlás optimalizálása: Szelepek mérete irányonként
- Az ellenőrzés összetettsége: Aszimmetrikus válasz kezelése
- Pontossági követelmények: A sebességváltozások figyelembevétele
Nehézipari alkalmazások
- Nagy rudak: Szerkezeti szilárdság prioritás
- Erőkompenzáció: Elfogadja a csökkentett behúzóerőt
- Terheléselemzés: Mindkét irányban megfelelő képesség biztosítása
- Biztonsági tényezők: Konzervatív tervezési megközelítés
Teljesítményfigyelés
Kulcsteljesítménymutatók
- Ciklusidő konzisztencia: A sebességváltozások figyelése
- Erő kimenet: Ellenőrizze a megfelelő képességet
- Energiafogyasztás: A levegőhasználati szokások nyomon követése
- Rendszernyomás: Optimalizálja a hatékonyságot
Hibaelhárítási iránymutatások
- Lassú visszahúzódás: Ellenőrizze a túlzott rúdterületet
- Elégtelen erő: A tényleges terület számításainak ellenőrzése
- Egyenetlen sebességek: Állítsa be az áramlásszabályozást
- Magas energiafelhasználás: Rúdméret kiválasztásának optimalizálása
Fejlett teljesítmény koncepciók
Dinamikus válasz
- Gyorsulási különbségek: Tömeg- és területi hatások
- Rezonancia jellemzők: Természetes frekvenciaváltozások
- Szabályozási stabilitás: Aszimmetrikus rendszer viselkedése
- Helymeghatározási pontosság: A sebességkülönbség hatásai
Hőhatások
- Hőtermelés: Kiterjesztési irányban magasabb
- Hőmérséklet emelkedés: Befolyásolja a teljesítmény konzisztenciáját
- Hűtési követelmények: Fokozott hőelvezetésre lehet szükség
- Anyagbővülés: Hőnövekedési megfontolások
Valós világbeli teljesítményadatok
Esettanulmány eredményei
100 létesítmény elemzése kimutatta:
- Szabványos rúdarányok: 10-15% sebességkülönbség tipikusan
- Túlméretezett rudak: Akár 50% sebességnövekedés behúzáskor
- Alulméretezett rudak: Szerkezeti hibák 25% esetben
- Optimalizált tervek: Kiegyensúlyozott teljesítmény érhető el
Amikor Lisa, egy brit csomagolómérnök számára optimalizáltam a henger kiválasztását, a rúdméretét 0,6-os furatarányról 0,5-re csökkentettük, így 20%-tal javítottuk az erőegyensúlyt, miközben megőriztük a megfelelő szerkezeti szilárdságot, és 30%-tal csökkentettük a ciklusidő-változásokat.
Következtetés
A rúd területe π(d/2)² a d átmérőjű rúddal. Ez a terület csökkenti a hatékony behúzóerőt a kettős működésű hengereknél, ami olyan sebesség- és erőkülönbségeket eredményez, amelyeket figyelembe kell venni a pneumatikus rendszer tervezésénél.
GYIK a rúd területéről
Hogyan kell kiszámítani a rúd területét?
Számítsuk ki a rúd területét A = π(d/2)² segítségével, ahol "d" a rúd átmérője, vagy A = πr², ahol "r" a rúd sugara. Egy 20 mm átmérőjű rúd esetében: A = π(10)² = 314,2 mm².
Miért fontos a rúdfelület a pneumatikus hengereknél?
A rúd területe csökkenti a dugattyú effektív felületét a kettős működésű hengerek behúzásakor, ami a behúzási erőhöz képest kisebb behúzási erőt eredményez. Ez befolyásolja az erőszámításokat, a sebességi jellemzőket és a rendszer teljesítményét.
Hogyan befolyásolja a rúd területe a henger erősségét?
A rúd területe csökkenti a behúzóerőt az összeggel: (dugattyú területe - rúd területe). Egy 20 mm-es rúd egy 63 mm-es hengerben körülbelül 10%-vel csökkenti a behúzóerőt a kinyújtóerőhöz képest.
Mi történik, ha a számítások során figyelmen kívül hagyjuk a rúd területét?
A rúdterület figyelmen kívül hagyása túlbecsült behúzóerő-számításokhoz, a behúzási terhelésekhez alulméretezett hengerekhez, helytelen sebesség-előrejelzésekhez és potenciális rendszerhibákhoz vezet, amikor a tényleges teljesítmény nem felel meg a tervezési elvárásoknak.
Hogyan befolyásolja a rúdméret a henger teljesítményét?
A nagyobb rudak jobban csökkentik a behúzóerőt, de a kisebb hatásos terület miatt növelik a behúzási sebességet. A standard rúdarányok (d/D = 0,5) a legtöbb alkalmazásban jó egyensúlyt biztosítanak a szerkezeti szilárdság és az erőszimmetria között.
-
A gyűrűs terület meghatározásának és számításának megértése mérnöki kontextusban. ↩
-
Fedezze fel a Pascal-törvényt, amely a folyadékhajtású rendszerek működését szabályozza. ↩
-
Ismerje meg a szerkezeti csavarodás elveit, amely a tömörítés alatt álló karcsú alkatrészek kritikus meghibásodási módja. ↩
-
Tekintse át az áramlási sebesség meghatározását és annak szerepét a folyadékrendszerek sebességének kiszámításában. ↩



