Folyamatosan küszködik a pneumatikus rendszer számításaival? Sok mérnök szembesül ugyanezzel a problémával a pneumatikus rendszerek tervezésekor vagy hibaelhárításakor. A jó hír az, hogy néhány kulcsfontosságú egyenlet elsajátítása megoldhatja a legtöbb pneumatikus kihívást.
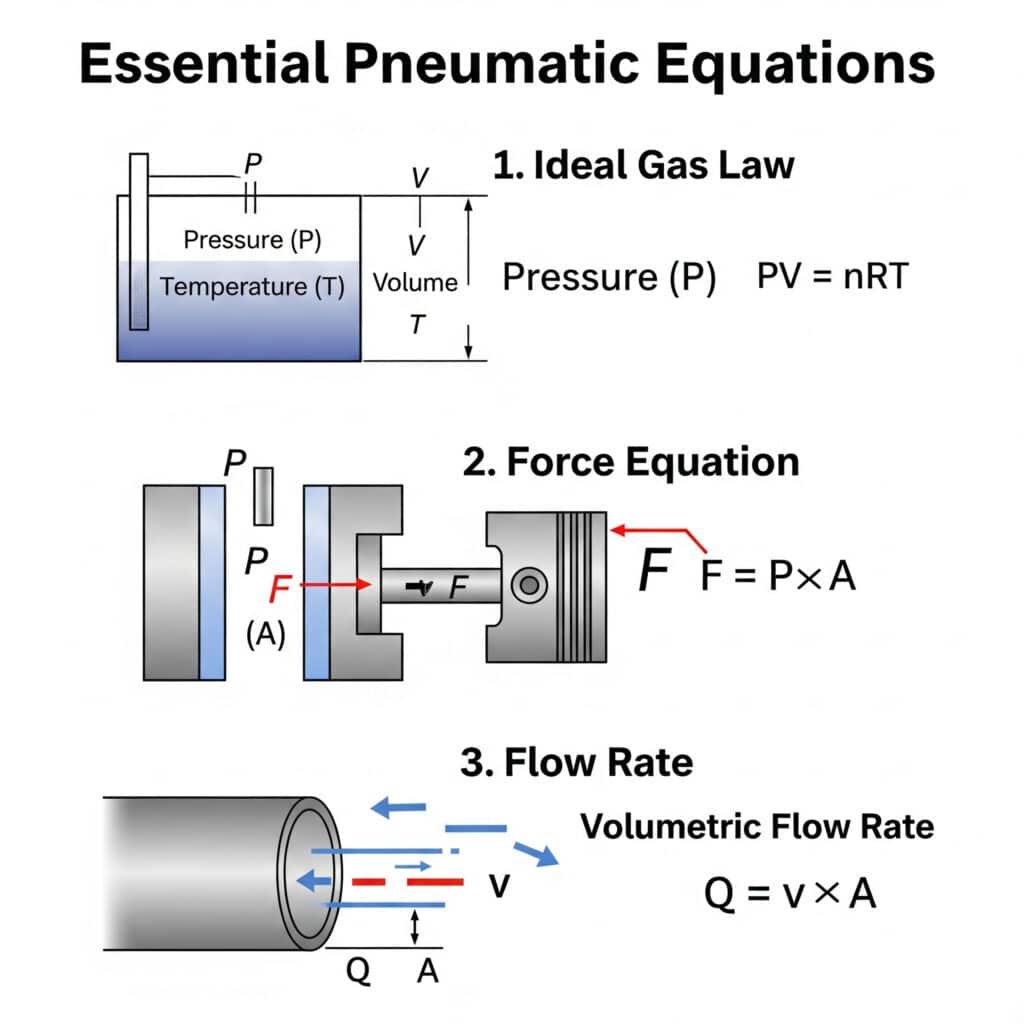
Az alapvető pneumatikus erőátviteli egyenletek, amelyeket minden mérnöknek ismernie kell, a következőket tartalmazzák ideális gáztörvény (PV = nRT)1, az erőegyenlet (F = P × A) és az áramlási sebesség összefüggése (Q = v × A). Ezen alapok megértése lehetővé teszi a pontos rendszertervezést és hibaelhárítást.
Több mint 15 éve dolgozom pneumatikus rendszerekkel a Beptónál, és saját bőrömön tapasztaltam, hogy ezeknek az alapvető egyenleteknek a megértése több ezer dollárnyi állásidőt takaríthat meg, és megelőzheti a költséges tervezési hibákat.
Tartalomjegyzék
- Gázegyenlet levezetése: Miért fontos a PV = nRT a pneumatikus rendszerekben?
- Hogyan viszonyul egymáshoz az erő, a nyomás és a terület a pneumatikus hengerekben?
- Mi a kapcsolat az áramlási sebesség és a sebesség között a pneumatikus rendszerekben?
- Következtetés
- GYIK a pneumatikus átviteli egyenletekről
Gázegyenlet levezetése: Miért fontos a PV = nRT a pneumatikus rendszerekben?
A pneumatikus rendszerek tervezésekor döntő fontosságú annak megértése, hogy a gázok hogyan viselkednek a különböző körülmények között. Ez a tudás jelentheti a különbséget a megbízhatóan működő és a váratlanul meghibásodó rendszer között.
Az ideális gáztörvény (PV = nRT) alapvető fontosságú a pneumatikus rendszerek számára, mivel leírja a nyomás, a térfogat és a hőmérséklet kölcsönhatását. Ez az összefüggés segít a mérnököknek megjósolni, hogyan viselkedik a levegő a rúd nélküli hengerekben és más pneumatikus alkatrészekben különböző üzemi körülmények között.
Az ideális gázok törvénye elméleti fogalomnak tűnhet a fizikaórán, de közvetlen gyakorlati alkalmazásai vannak a pneumatikus rendszerekben. Hadd bontsam le ezt gyakorlatiasabb fogalmakra.
A PV = nRT változóinak megértése
| Változó | Jelentése | Pneumatikus alkalmazás |
|---|---|---|
| P | Nyomás | Üzemi nyomás a rendszerben |
| V | Kötet | Légkamra mérete hengerben |
| n | Molok száma | A rendszerben lévő levegő mennyisége |
| R | Gázkonstans2 | Univerzális állandó (8,314 J/mol-K) |
| T | Hőmérséklet | Üzemi hőmérséklet |
Hogyan befolyásolja a hőmérséklet a pneumatikus teljesítményt?
A hőmérséklet-változások jelentősen befolyásolhatják a pneumatikus rendszer teljesítményét. Tavaly egyik németországi ügyfelünk, Hans, megkeresett engem a rúd nélküli hengeres rendszerének következetlen teljesítménye miatt. A rendszer reggel tökéletesen működött, de délutánra elvesztette a teljesítményét.
Miután elemeztük a berendezését, kiderült, hogy a rendszer közvetlen napfénynek volt kitéve, ami 15°C-os hőmérséklet-emelkedést okozott. Az ideális gáztörvényt használva kiszámítottuk, hogy ez a hőmérsékletváltozás közel 5% nyomásváltozást okozott. Megfelelő szigetelést szereltünk fel, és a probléma azonnal megoldódott.
A gáztörvény gyakorlati alkalmazása a pneumatikus tervezésben
Pneumatikus rendszerek tervezésekor a rúd nélküli hengerek, a gáztörvény segít nekünk:
- A hőmérséklet-ingadozás miatti nyomásváltozások kiszámítása
- A légtartályok térfogatigényének meghatározása
- Az erőkifejtés változásainak előrejelzése különböző körülmények között
- A kompresszorok méretezése az alkalmazásnak megfelelően
Hogyan viszonyul egymáshoz az erő, a nyomás és a terület a pneumatikus hengerekben?
Az erő, a nyomás és a terület közötti kapcsolat megértése alapvető fontosságú a megfelelő rúd nélküli henger kiválasztásakor. Ez a tudás biztosítja a szükséges teljesítményt anélkül, hogy túlköltekezne.
A erő-nyomás-terület kapcsolat3 a pneumatikus hengerekben az F = P × A, ahol F az erő (N), P a nyomás (Pa) és A az effektív terület (m²). Ez az egyenlet lehetővé teszi a mérnökök számára, hogy kiszámítsák a rúd nélküli hengerek pontos erőkifejtését különböző üzemi nyomások mellett.
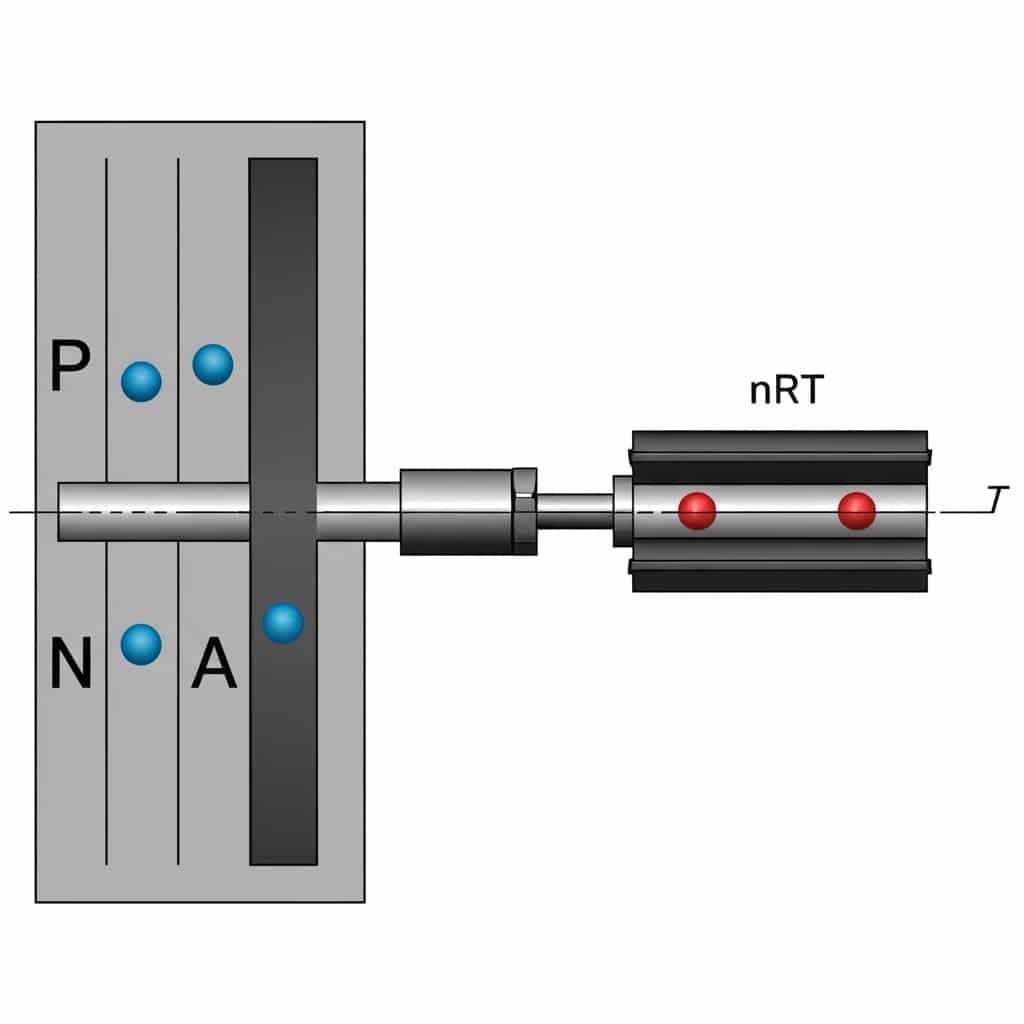
Ez az egyszerű egyenlet az alapja minden pneumatikus erőszámításnak, de számos gyakorlati szempontot sok mérnök figyelmen kívül hagy.
Hatékony terület számításai különböző henger típusok esetén
A hatásos terület a henger típusától függően változik:
| Henger típusa | Hatékony terület kiszámítása | Megjegyzések |
|---|---|---|
| Egyszeri működésű | A = πr² | Teljes furat területe |
| Dupla működésű (hosszabbító) | A = πr² | Teljes furat területe |
| Dupla működésű (behúzás) | A = π(r² - r'²) | r' a rúd sugara |
| Rúd nélküli henger | A = πr² | Következetes mindkét irányban |
Valós világbeli erőhatékonysági tényezők
A gyakorlatban a tényleges erőkifejtést a következők befolyásolják:
- Súrlódási veszteségek: Jellemzően 3-20% a tömítés kialakításától függően
- Nyomáscsökkenés: Az effektív nyomást 5-10%-vel csökkentheti.
- Dinamikus hatások: A gyorsító erők csökkenthetik a rendelkezésre álló erőt
Emlékszem, hogy együtt dolgoztam Sarah-val, egy gépészmérnökkel, aki egy csomagolóipari vállalatnál dolgozott az Egyesült Királyságban. Egy új gépet tervezett, és kiszámolta, hogy a szükséges erő eléréséhez 63 mm-es furattal rendelkező rúd nélküli hengerre van szüksége. Azonban nem számolt a súrlódási veszteségekkel.
Azt javasoltuk, hogy növelje a henger átmérőjét 80 mm-es furatú hengerre, amely elegendő többleterőt biztosított a súrlódás leküzdéséhez, miközben fenntartotta a kívánt teljesítményt. Ez az egyszerű beállítás megmentette őt a beszerelés utáni költséges újratervezéstől.
Az elméleti és a tényleges erőkifejtés összehasonlítása
A rúd nélküli hengerek kiválasztásakor mindig ajánlom:
- Számítsuk ki az elméleti erőt az F = P × A módszerrel.
- A legtöbb alkalmazásnál 25% biztonsági tényezőt kell alkalmazni.
- Ellenőrizze a számításokat a gyártótól származó tényleges teljesítményadatokkal.
- Adott esetben vegye figyelembe a dinamikus terhelési körülményeket
Mi a kapcsolat az áramlási sebesség és a sebesség között a pneumatikus rendszerekben?
Az áramlási sebesség és a sebesség kritikus paraméterek, amelyek meghatározzák, hogy a pneumatikus rendszer milyen gyorsan reagál. Ennek az összefüggésnek a megértése segít megelőzni a lassú teljesítményt, és biztosítja, hogy a rendszer megfeleljen a ciklusidőre vonatkozó követelményeknek.
A kapcsolat a áramlási sebesség (Q) és sebesség (v)4 a pneumatikus rendszerekben a Q = v × A, ahol Q a térfogatáram, v a levegő sebessége, A pedig az átjáró keresztmetszeti területe. Ez az egyenlet kulcsfontosságú a légvezetékek és szelepek megfelelő méretezéséhez.
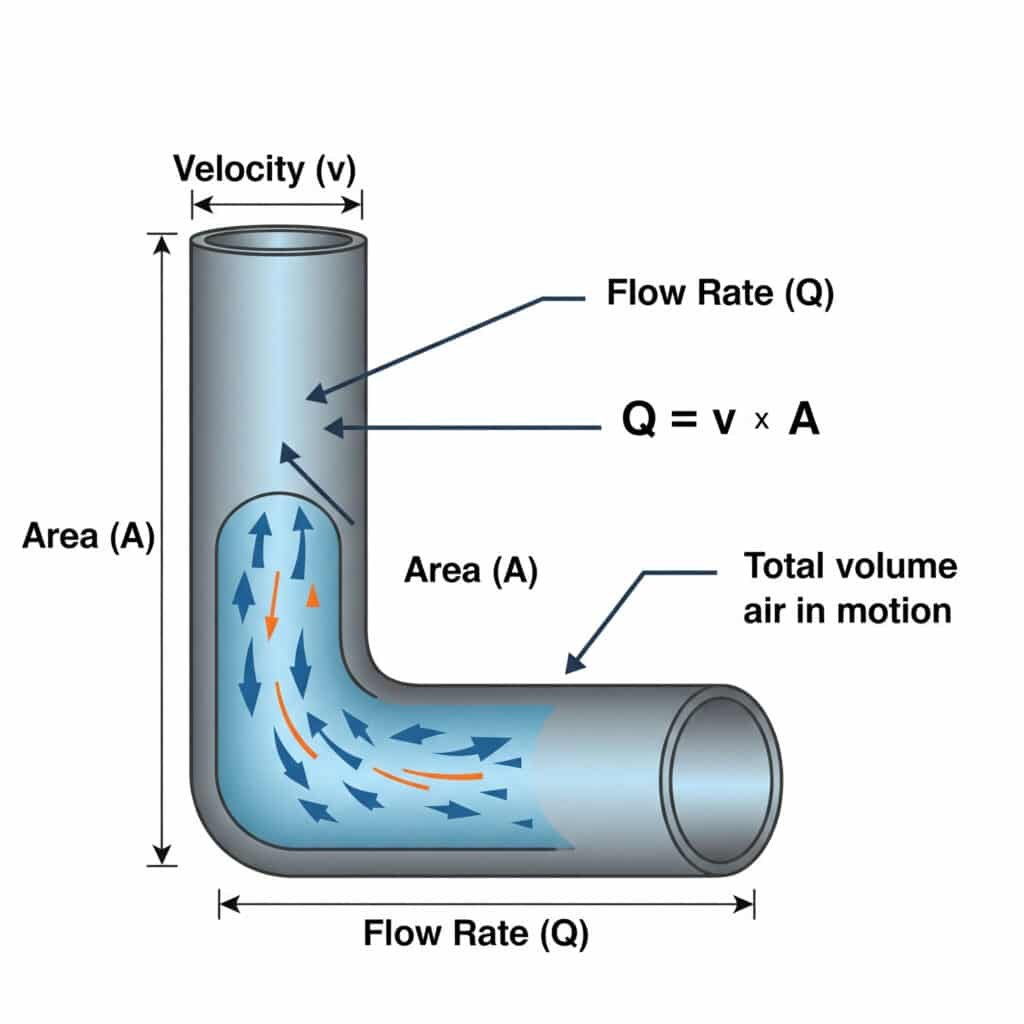
Számos pneumatikus rendszerprobléma a levegőellátó alkatrészek helytelen méretezéséből ered. Vizsgáljuk meg, hogyan befolyásolja ez az egyenlet a valós teljesítményt.
Kritikus áramlási sebességek a gyakori pneumatikus alkatrészekhez
A különböző alkatrészeknek eltérő áramlási követelményeik vannak:
| Komponens | Tipikus áramlási sebesség követelmény | Az alulméretezés hatása |
|---|---|---|
| Rúd nélküli henger (25mm furat) | 15-30 L/min | Lassú működés, csökkentett erő |
| Rúd nélküli henger (63mm furat) | 60-120 L/min | Következetlen mozgás |
| Irányváltó szelep | Méret szerint változik | Nyomáscsökkenés, lassú reakció |
| Levegő előkészítő egység | Rendszer összesen + 30% | Nyomásingadozás |
Hogyan befolyásolja a csőátmérő a rendszer teljesítményét?
A légvezetékek átmérője drámai hatással van a rendszer teljesítményére:
- Nyomáscsökkenés: A sebesség négyzetével nő
- Válaszidő: A kisebb vonalak nagyobb sebességet, de nagyobb ellenállást jelentenek.
- Energiahatékonyság: A nagyobb vezetékek csökkentik a nyomásesést, de növelik a költségeket
A megfelelő vezetékméretek kiszámítása pneumatikus rendszerekhez
A rúd nélküli henger alkalmazásához szükséges légvezetékek megfelelő méretezése:
- A szükséges áramlási sebesség meghatározása a henger mérete és a ciklusidő alapján
- Számítsa ki a megengedett legnagyobb nyomásesést (általában 0,1 bar vagy annál kisebb).
- Olyan vezetékátmérő kiválasztása, amely a sebességet 15-20 m/s alatt tartja.
- Ellenőrizze a szelep áramlási kapacitását (Cv vagy Kv érték5) megfelel a rendszerkövetelményeknek
Egyszer segítettem egy franciaországi ügyfélnek, akinek a nagy kompresszor ellenére lassú volt a henger mozgása. A probléma nem az elégtelen levegőtermelés volt, hanem az, hogy a 6 mm-es csövek túlzott ellenállást képeztek. A 10 mm-es csövekre való frissítés azonnal megoldotta a problémát, és 40%-vel növelte a gép ciklussebességét.
Következtetés
E három alapvető pneumatikai egyenlet - az ideális gáztörvény, az erő-nyomás-terület kapcsolat és az áramlási sebesség-sebesség kapcsolat - megértése biztosítja a sikeres pneumatikai rendszertervezés alapját. Ezen elvek alkalmazásával kiválaszthatja a megfelelő rúd nélküli henger alkatrészeket, hatékonyan elháríthatja a problémákat, és optimalizálhatja a rendszer teljesítményét.
GYIK a pneumatikus átviteli egyenletekről
Mi az ideális gáztörvény, és miért fontos a pneumatikus rendszerek esetében?
Az ideális gáztörvény (PV = nRT) leírja, hogy a nyomás, a térfogat, a hőmérséklet és a gázmennyiség hogyan viszonyul egymáshoz egy pneumatikus rendszerben. Azért fontos, mert segít a mérnököknek megjósolni, hogy a változó körülmények (különösen a hőmérséklet) hogyan befolyásolják a rendszer teljesítményét és a nyomásigényt.
Hogyan számolhatom ki egy rúd nélküli henger erőleadását?
Számítsa ki a leadott erőt a nyomás és az effektív terület szorzataként (F = P × A). A rúd nélküli hengereknél a hatásos terület mindkét irányban azonos, így az erőszámítás egyszerűbb, mint a hagyományos hengereknél, amelyeknél a kitolási és behúzási erők eltérőek.
Mi a különbség az áramlási sebesség és a sebesség között a pneumatikus rendszerekben?
Az áramlási sebesség a rendszeren egységnyi idő alatt áthaladó levegő térfogata (jellemzően L/min-ben), míg a sebesség az a sebesség, amellyel a levegő áthalad egy csatornán (m/s-ban). A két értéket a Q = v × A egyenlet kapcsolja össze, ahol A az átjáró keresztmetszeti területe.
Hogyan befolyásolja a hőmérséklet a pneumatikus rendszer teljesítményét?
Az ideális gáztörvény szerint a hőmérséklet közvetlenül befolyásolja a nyomást. A hőmérséklet 10°C-os növekedése körülbelül 3,5%-vel növeli a nyomást, ha a térfogat állandó marad. Ez nyomásváltozásokat okozhat, befolyásolhatja a tömítés teljesítményét, és megváltoztathatja a rúd nélküli hengerek erőkifejtését.
Mi a leggyakoribb oka a nyomásesésnek a pneumatikus rendszerekben?
A nyomásesés leggyakoribb okai az alulméretezett légvezetékek, a szűkítő szerelvények és a nem megfelelő szelepáramlási kapacitás. Az áramlási egyenlet szerint a kisebb átmenetek nagyobb légsebességet igényelnek, ami exponenciálisan növeli az ellenállást és a nyomásesést.
Hogyan méretezzem megfelelően a légvezetékeket egy rúd nélküli hengerhez?
A légvezetékek méretezése a szükséges áramlási sebesség kiszámításával történik a henger térfogata és a ciklusidő alapján, majd olyan vezetékátmérő kiválasztásával, amely a nyomásesés minimalizálása érdekében 15-20 m/s alatt tartja a levegő sebességét. A legtöbb rúd nélküli hengeres alkalmazásnál a 8-12 mm-es vezetékek megfelelő egyensúlyt biztosítanak a teljesítmény és a költségek között.
-
Részletes magyarázatot ad az ideális gáztörvényről, egy hipotetikus ideális gáz alapvető állapotegyenletéről, amely számos gáz viselkedését közelíti meg különböző körülmények között. ↩
-
Megmagyarázza az egyetemes gázállandó (R) szerepét és értékét az ideális gáztörvényben, amely az energiaskálákat a hőmérsékleti skálákkal összekötő fizikai állandóként szolgál. ↩
-
Alapvető magyarázatot ad a nyomásról, amelyet egy tárgy felületére merőlegesen kifejtett erőként definiálnak egységnyi területre vonatkoztatva, amelyen az erő eloszlik. ↩
-
Részletesen ismerteti a folytonossági egyenlet elvét, amely a folyadékdinamika egyik alapvető fogalma, és amely kimondja, hogy egy összenyomhatatlan folyadék esetében a tömegáramlásnak állandónak kell lennie a cső egyik keresztmetszetétől a másikig. ↩
-
Megadja az áramlási együttható (Cv) és az áramlási tényező (Kv) műszaki meghatározását, amelyek szabványosított értékek, amelyeket a különböző szelepek áramlási kapacitásainak összehasonlítására használnak. ↩
English 
Deutsch 
Français 
Italiano 
Español 
Português 
Русский 
العربية 
日本語 
한국어 
Bahasa Indonesia 
Türkçe 
Nederlands 
Ελληνικά 
Български 
Čeština 
Dansk 
Eesti 
Suomi 
Magyar 
Lietuvių kalba 
Latviešu valoda 
Polski 
Română 
Svenska 
Slovenčina 
Slovenščina 
Norsk bokmål 
Українська