A pneumatikus elméleti tévhitek évente több mint $30 milliárd forintba kerülnek a gyártóknak a nem hatékony tervezés és a rendszerhibák miatt. A mérnökök a pneumatikus rendszereket gyakran egyszerűsített hidraulikus rendszerekként kezelik, figyelmen kívül hagyva a levegő alapvető viselkedési elveit. A pneumatikai elmélet megértése megelőzi a katasztrofális tervezési hibákat, és felszabadítja a rendszer optimalizálásának lehetőségeit.
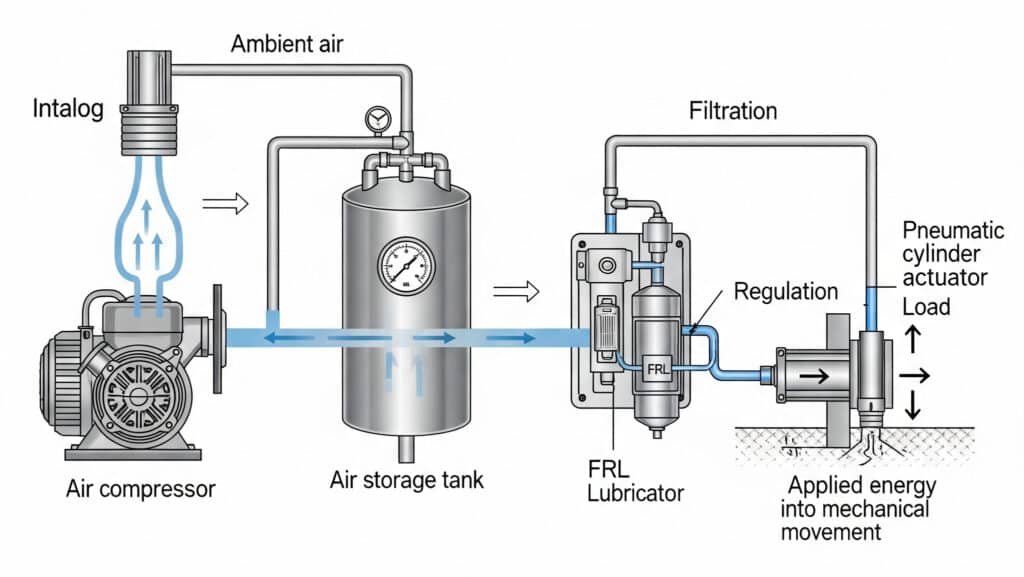
A pneumatika elmélete a sűrített levegő energiaátalakításán alapul, ahol a légköri levegőt a potenciális energia tárolása érdekében sűrítik, az elosztórendszereken keresztül továbbítják, és a működtetőkön keresztül mechanikai munkává alakítják, amelyet a következők szabályoznak. termodinamikai elvek1 és a folyadékmechanika.
Hat hónappal ezelőtt egy Erik Lindqvist nevű svéd automatizálási mérnökkel dolgoztam együtt, akinek a gyári pneumatikus rendszere 40%-tal több energiát fogyasztott a tervezettnél. Csapata alapvető nyomásszámításokat alkalmazott anélkül, hogy megértette volna a pneumatikai elmélet alapjait. A megfelelő pneumatikai elméleti alapelvek bevezetése után 45%-tal csökkentettük az energiafogyasztást, miközben 60%-tal javítottuk a rendszer teljesítményét.
Tartalomjegyzék
- Melyek a pneumatika elméletének alapelvei?
- Hogyan hoz létre a levegő kompressziója pneumatikus energiát?
- Melyek a pneumatikus rendszerek termodinamikai alapelvei?
- Hogyan alakítják át a pneumatikus alkatrészek a levegő energiáját mechanikai munkává?
- Milyen energiaátviteli mechanizmusok vannak a pneumatikus rendszerekben?
- Hogyan alkalmazható a pneumatika elmélete az ipari rendszerek tervezésénél?
- Következtetés
- GYIK a pneumatikus elméletről
Melyek a pneumatika elméletének alapelvei?
A pneumatika elmélete magában foglalja a sűrített levegős rendszereket irányító tudományos elveket, beleértve az energia átalakítását, átvitelét és felhasználását az ipari alkalmazásokban.
A pneumatika elmélete a termodinamikai energiaátalakításon, a levegőáramlás áramlástanán, az erőkifejtés mechanikai elvein és a rendszer automatizálásának vezérléselméletén alapul, integrált sűrített levegős energiarendszereket hozva létre.
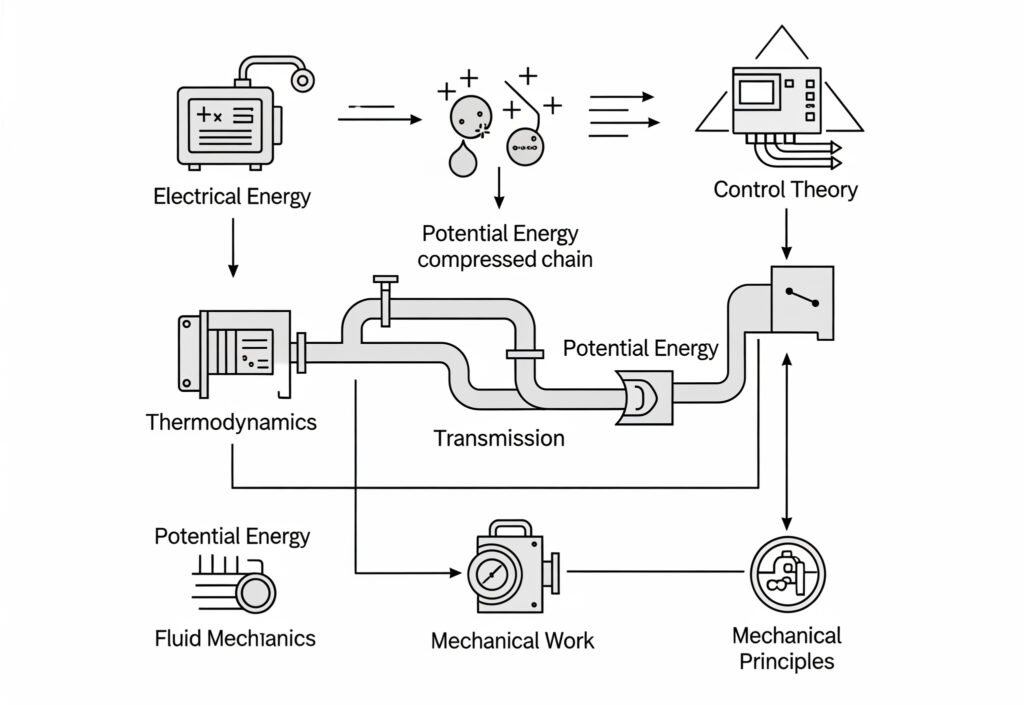
Energiaátalakítási lánc
A pneumatikus rendszerek szisztematikus energiaátalakítási folyamaton keresztül működnek, amely az elektromos energiát sűrített levegőn keresztül mechanikai munkává alakítja át.
Energiaátalakítási sorrend:
- Elektromosból mechanikusba: Elektromos motor hajtja a kompresszort
- Mechanikus to Pneumatikus: A kompresszor sűrített levegőt állít elő
- Pneumatikus tárolás: Receptorokban tárolt sűrített levegő
- Pneumatikus sebességváltó: A levegő elosztása csővezetéken keresztül
- Pneumatikusból mechanikusba: A működtetők a légnyomást munkává alakítják
Energiahatékonysági elemzés:
| Átalakítási szakasz | Tipikus hatékonyság | Energia veszteség források |
|---|---|---|
| Elektromos motor | 90-95% | Hő, súrlódás, mágneses veszteségek |
| Légkompresszor | 80-90% | Hő, súrlódás, szivárgás |
| Levegőelosztás | 85-95% | Nyomásesés, szivárgás |
| Pneumatikus működtető | 80-90% | Súrlódás, belső szivárgás |
| Általános rendszer | 55-75% | Halmozott veszteségek |
Sűrített levegő mint energiahordozó
A sűrített levegő a pneumatikus rendszerekben energiaátviteli közegként szolgál, amely a nyomáspotenciálon keresztül tárolja és szállítja az energiát.
Levegős energiatárolás alapelvei:
Tárolt energia = P × V × ln(P/P₀)
Hol:
- P = Sűrített levegő nyomása
- V = Tárolási térfogat
- P₀ = légköri nyomás
Energiasűrűség-összehasonlítás:
- Sűrített levegő (100 PSI): 0,5 BTU köbméterenként
- Hidraulikafolyadék (1000 PSI): 0,7 BTU köbméterenként
- Elektromos akkumulátor: 50-200 BTU köbméterenként
- Benzin: 36,000 BTU gallononként
Rendszerintegrációs elmélet
A pneumatika elmélete olyan rendszerintegrációs elveket foglal magában, amelyek optimalizálják az alkatrészek kölcsönhatását és az általános teljesítményt.
Integrációs elvek:
- Nyomás illesztés: Kompatibilis nyomásra tervezett alkatrészek
- Flow Matching: A levegőellátás megfelel a fogyasztási követelményeknek
- Válaszillesztés: Az alkalmazáshoz optimalizált rendszeridőzítés
- Ellenőrzési integráció: Koordinált rendszerüzemeltetés
Alapvető irányadó egyenletek
A pneumatikai elmélet a rendszer viselkedését és teljesítményét leíró alapvető egyenletekre támaszkodik.
Pneumatikus egyenletek:
| Elvileg | Egyenlet | Alkalmazás |
|---|---|---|
| Ideális gáztörvény2 | PV = nRT | A levegő viselkedésének előrejelzése |
| Erő generálása | F = P × A | A működtető erő kimenete |
| Áramlási sebesség | Q = Cd × A × √(2ΔP/ρ) | Légáramlási számítások |
| Munka kimenete | W = P × ΔV | Energiaátalakítás |
| Teljesítmény | P = F × v | A rendszer energiaigénye |
Hogyan hoz létre a levegő kompressziója pneumatikus energiát?
A légsűrítés a légköri levegőt a térfogat csökkentése és a nyomás növelése révén nagy energiájú sűrített levegővé alakítja át, létrehozva a pneumatikus rendszerek energiaforrását.
A levegő kompressziója termodinamikai folyamatok révén pneumatikus energiát hoz létre, amikor a mechanikai munka összenyomja a légköri levegőt, és a megnövekedett nyomás formájában potenciális energiát tárol, amely hasznos munka elvégzéséhez felszabadítható.
Kompressziós termodinamika
A légsűrítés termodinamikai elveket követ, amelyek meghatározzák az energiaszükségletet, a hőmérsékletváltozást és a rendszer hatékonyságát.
Tömörítési folyamat típusok:
| Folyamat típusa | Jellemzők | Energia egyenlet | Alkalmazások |
|---|---|---|---|
| Izotermikus3 | Állandó hőmérséklet | W = P₁V₁ln(P₂/P₁) | Lassú sűrítés hűtéssel |
| Adiabatikus | Nincs hőátadás | W = (P₂V₂-P₁V₁)/(γ-1) | Gyors tömörítés |
| Polytropikus | Valós világbeli folyamat | W = (P₂V₂-P₁V₁)/(n-1) | A kompresszor tényleges működése |
Hol:
- γ = fajlagos hőhányad (levegő esetében 1,4)
- n = Polytrópikus exponens (1,2-1,35 tipikus)
Kompresszor típusok és elmélet
A különböző kompresszortípusok különböző mechanikai elveket alkalmaznak a levegő sűrítésének eléréséhez.
Pozitív kiszorítású kompresszorok:
Dugattyús kompresszorok:
- Elmélet: A dugattyú mozgása térfogatváltozást okoz
- Tömörítési arány: P₂/P₁ = (V₁/V₂)ⁿ
- Hatékonyság: 70-85% térfogati hatásfok
- Alkalmazások: Nagynyomású, szakaszos üzem
Rotációs csavarkompresszorok:
- Elmélet: A hálós rotorok csapdába ejtik és összenyomják a levegőt
- Tömörítés: Folyamatos folyamat
- Hatékonyság: 85-95% térfogati hatásfok
- Alkalmazások: Folyamatos üzem, mérsékelt nyomás
Dinamikus kompresszorok:
Centrifugális kompresszorok:
- Elmélet: A járókerék mozgási energiát közvetít, amelyet nyomássá alakít át.
- Nyomás emelkedés: ΔP = ρ(U₂² - U₁²)/2
- Hatékonyság: 75-85% teljes hatékonyság
- Alkalmazások: Nagy térfogat, alacsony vagy közepes nyomás
Tömörítési energiaigény
A légsűrítés elméleti és tényleges energiaszükséglete határozza meg a rendszer energiaigényét és üzemeltetési költségeit.
Elméleti kompressziós teljesítmény:
Izotermikus energia: P = (mRT/550) × ln(P₂/P₁)
Adiabatikus teljesítmény: P = (mRT/550) × (γ/(γ-1)) × [(P₂/P₁)^((γ-1)/γ) - 1]
Tényleges energiaigény:
Fékezési lóerő = elméleti teljesítmény / teljes hatásfok
Energiafogyasztási példák:
| Nyomás (PSI) | CFM | Elméleti HP | Tényleges HP (75% eff) |
|---|---|---|---|
| 100 | 100 | 18.1 | 24.1 |
| 100 | 500 | 90.5 | 120.7 |
| 150 | 100 | 23.8 | 31.7 |
| 200 | 100 | 28.8 | 38.4 |
Hőtermelés és hőgazdálkodás
A levegő tömörítése jelentős hőt termel, amelyet a rendszer hatékonysága és az alkatrészek védelme érdekében kezelni kell.
Hőtermelés elmélete:
Termelt hő = bemenő munka - hasznos kompressziós munka
Adiabatikus tömörítés esetén:
Hőmérséklet-emelkedés = T₁[(P₂/P₁)^((γ-1)/γ) - 1]
Hűtési módszerek:
- Levegő hűtés: Természetes vagy kényszerített légkeringetés
- Vízhűtés: A hőcserélők eltávolítják a tömörítési hőt
- Hűtésközi hűtés: Többlépcsős sűrítés közbenső hűtéssel
- Utóhűtés: Végső hűtés a levegős tárolás előtt
Melyek a pneumatikus rendszerek termodinamikai alapelvei?
A termodinamikai elvek szabályozzák az energiaátalakítást, a hőátadást és a hatékonyságot a pneumatikus rendszerekben, meghatározva a rendszer teljesítményét és a tervezési követelményeket.
A pneumatikus termodinamika magában foglalja a termodinamika első és második törvényét, a gázok viselkedési egyenleteit, a hőátadási mechanizmusokat és a rendszer hatékonyságát és teljesítményét befolyásoló entrópia megfontolásokat.
A termodinamika első törvénye Alkalmazás
A termodinamika első törvénye szabályozza az energia megőrzését a pneumatikus rendszerekben, a munkabefektetés, a hőátadás és a belső energiaváltozás összefüggésében.
Az első törvény egyenlete:
ΔU = Q - W
Hol:
- ΔU = A belső energia változása
- Q = A rendszerhez hozzáadott hő
- W = A rendszer által végzett munka
Pneumatikus alkalmazások:
- Tömörítési folyamat: A munkabefektetés növeli a belső energiát és a hőmérsékletet
- Bővítési folyamat: A belső energia csökken a munka elvégzésével
- Hőátvitel: Befolyásolja a rendszer hatékonyságát és teljesítményét
- Energiaegyensúly: A teljes energiabevitel egyenlő hasznos munka plusz veszteségek
A termodinamika második törvénye Hatás
A második törvény meghatározza a maximális elméleti hatékonyságot, és azonosítja a rendszer teljesítményét csökkentő irreverzibilis folyamatokat.
Entrópia megfontolások:
ΔS ≥ Q/T (irreverzibilis folyamatok esetén)
Irreverzibilis folyamatok pneumatikus rendszerekben:
- Súrlódási veszteségek: A mechanikai energia átalakítása hővé
- Veszteségek megfékezése: Nyomáscsökkenés munkateljesítmény nélkül
- Hőátvitel: A hőmérsékletkülönbségek entrópiát hoznak létre
- Keverési folyamatok: Különböző nyomású áramlatok keveredése
Gáz viselkedése pneumatikus rendszerekben
A valós gáz viselkedése bizonyos körülmények között eltér az ideális gázra vonatkozó feltételezésektől, ami befolyásolja a rendszer teljesítményének számításait.
Ideális gáz feltételezések:
- Térfogat nélküli pontmolekulák
- Nincsenek intermolekuláris erők
- Csak rugalmas ütközések
- A mozgási energia a hőmérséklettel arányos
Valódi gázkorrekciók:
Van der Waals-egyenlet: (P + a/V²)(V - b) = RT
Ahol a és b gázspecifikus konstansok, amelyek a következőket veszik figyelembe:
- a: Molekulák közötti vonzóerők
- b: Molekuláris térfogathatások
Összenyomhatósági tényező4:
Z = PV/(nRT)
- Z = 1 ideális gáz esetén
- Z ≠ 1 a valós gáz viselkedése esetén
Hőátvitel pneumatikus rendszerekben
A hőátadás a légsűrűséget, a nyomást és az alkatrészek működését befolyásoló hőmérséklet-változásokon keresztül befolyásolja a pneumatikus rendszerek teljesítményét.
Hőátviteli módok:
| Mód | Mechanizmus | Pneumatikus alkalmazások |
|---|---|---|
| Vezetés | Közvetlen érintkezéses hőátadás | Csőfalak, alkatrészfűtés |
| Konvekció | Folyadékmozgás hőátadás | Léghűtés, hőcserélők |
| Sugárzás | Elektromágneses hőátadás | Magas hőmérsékletű alkalmazások |
Hőátviteli hatások:
- Levegő sűrűségének változása: A hőmérséklet befolyásolja a levegő sűrűségét és áramlását
- Komponens bővítés: A hőtágulás befolyásolja a távolságokat
- Nedvesség-kondenzáció: A hűtés vízképződést okozhat
- Rendszer hatékonysága: A hőveszteségek csökkentik a rendelkezésre álló energiát
Termodinamikai ciklusok pneumatikus rendszerekben
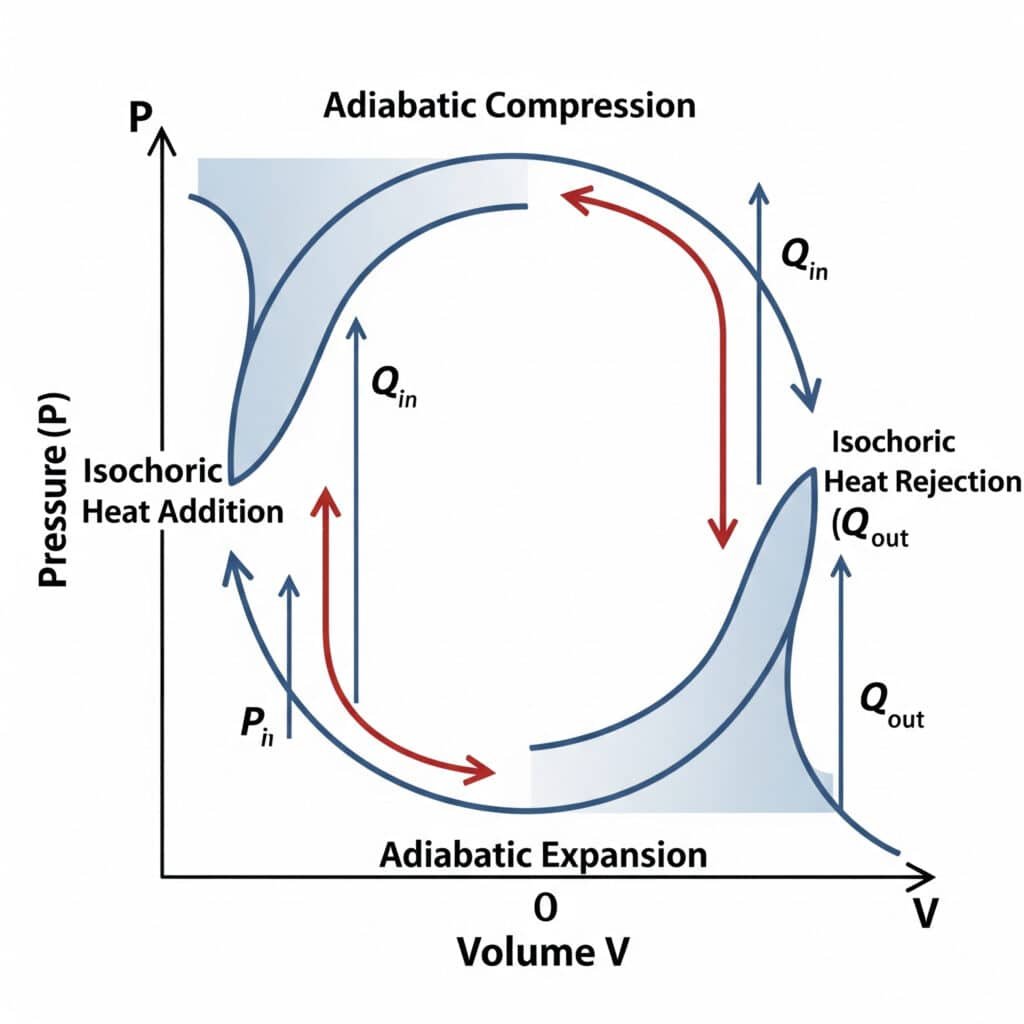
A pneumatikus rendszerek termodinamikai ciklusokon keresztül működnek, amelyek meghatározzák a hatékonyságot és a teljesítményjellemzőket.
Pneumatikus alapciklus:
- Tömörítés: Rendszernyomásig sűrített légköri levegő
- Tárolás: Állandó nyomáson tárolt sűrített levegő
- Bővítés: A levegő kitágul a működtetőkön keresztül a munka elvégzéséhez
- Kipufogó: A légkörbe kibocsátott, kitágult levegő
Ciklushatékonysági elemzés:
Ciklus hatásfok = Hasznos munka leadott teljesítmény / energiabevitel
Tipikus pneumatikus ciklus hatásfoka: 20-40% a következők miatt:
- Tömörítési elégtelenségek
- Hőveszteségek a tömörítés során
- Nyomáscsökkenés az elosztásban
- Tágulási veszteségek a működtetőkben
- Nem visszanyert kipufogógáz-energia
Nemrégiben segítettem egy Lars Andersen nevű norvég gyártómérnöknek optimalizálni a pneumatikus rendszer termodinamikáját. A megfelelő hővisszanyerés megvalósításával és a fojtási veszteségek minimalizálásával 28%-ről 41%-re javítottuk a rendszer teljes hatékonyságát, és 35%-tel csökkentettük az üzemeltetési költségeket.
Hogyan alakítják át a pneumatikus alkatrészek a levegő energiáját mechanikai munkává?
A pneumatikus alkatrészek a sűrített levegő energiáját hasznos mechanikai munkává alakítják különböző mechanizmusok segítségével, amelyek a nyomást és az áramlást erővé, mozgássá és nyomatékká alakítják.
A pneumatikus energiaátalakítás a lineáris erőhöz nyomás-térfogat összefüggéseket, a mozgáshoz nyomás-térfogat kiterjedést, a forgó mozgáshoz pedig speciális mechanizmusokat használ, amelyek hatékonyságát az alkatrészek kialakítása és a működési feltételek határozzák meg.
Lineáris működtető energiaátalakítás
Lineáris pneumatikus működtetők a légnyomást dugattyús-hengeres mechanizmusokon keresztül lineáris erővé és mozgássá alakítják.
Erőfejlesztés elmélete:
F = P × A - F_friction - F_spring
Hol:
- P = rendszernyomás
- A = hatásos dugattyúfelület
- F_friction = Súrlódási veszteségek
- F_spring = Visszatérő rugóerő (egyszeres működésű)
Munkakimeneti számítás:
Munka = erő × távolság = P × A × löket
Teljesítmény:
Teljesítmény = erő × sebesség = P × A × (ds/dt)
Henger típusok és teljesítmény
A különböző hengerkialakítások optimalizálják az energiaátalakítást az adott alkalmazásokhoz és teljesítménykövetelményekhez.
Egyszeres működésű hengerek:
- Energiaforrás: Sűrített levegő csak egy irányban
- Visszatérési mechanizmus: Rugós vagy gravitációs visszatérés
- Hatékonyság: 60-75% a rugóveszteségek miatt
- Alkalmazások: Egyszerű pozícionálás, kis erőkifejtésű alkalmazások
Dupla működtetésű hengerek:
- Energiaforrás: Sűrített levegő mindkét irányban
- Erő kimenet: Teljes nyomóerő mindkét irányban
- Hatékonyság: 75-85% megfelelő kialakítással
- Alkalmazások: Nagy erőkifejtés, precíziós alkalmazások
Teljesítmény-összehasonlítás:
| Henger típusa | Erő (Hosszabbítás) | Erő (visszahúzás) | Hatékonyság | Költségek |
|---|---|---|---|---|
| Egyszeri működésű | P × A - F_rugó | Csak F_spring | 60-75% | Alacsony |
| Kettős működésű | P × A | P × (A - A_rod) | 75-85% | Közepes |
| Rúd nélküli | P × A | P × A | 80-90% | Magas |
Rotációs működtető energiaátalakítás
A forgó pneumatikus működtetők a légnyomást különböző mechanikai elrendezéseken keresztül alakítják át forgó mozgássá és nyomatékká.
Vane-típusú forgó működtetők:
Nyomaték = P × A × R × η
Hol:
- P = rendszernyomás
- A = effektív szárnyfelület
- R = a lendítőkar sugara
- η = mechanikai hatásfok
Fogasléces és fogasléces működtetők:
Nyomaték = (P × A_dugattyú) × R_csapszeg
Ahol R_pinion a fogaskerék sugara, amely a lineáris erőt forgatónyomatékká alakítja.
Energiaátalakítási hatékonysági tényezők
A sűrített levegőből hasznos munkává alakított pneumatikus energia átalakításának hatékonyságát több tényező befolyásolja.
Hatékonysági veszteségforrások:
| Veszteség forrása | Tipikus veszteség | Enyhítési stratégiák |
|---|---|---|
| Súrlódás | 5-15% | Alacsony súrlódású tömítések, megfelelő kenés |
| Belső szivárgás | 2-10% | Minőségi tömítések, megfelelő hézagok |
| Nyomás cseppek | 5-20% | Megfelelő méretezés, rövid csatlakozások |
| Hőtermelés | 10-20% | Hűtés, hatékony kialakítás |
| Mechanikai súrlódás | 5-15% | Minőségi csapágyak, igazítás |
Átalakítás teljes hatékonysága:
η_total = η_tömítés × η_szivárgás × η_nyomás × η_mechanikai
Tipikus tartomány: 60-80% jól megtervezett rendszerek esetén
Dinamikus teljesítményjellemzők
A pneumatikus működtető teljesítménye a terhelési körülményektől, a sebességigénytől és a rendszer dinamikájától függően változik.
Erő-sebesség összefüggések:
Állandó nyomás és áramlás mellett:
- Nagy terhelés: Alacsony sebesség, nagy erő
- Alacsony terhelés: Nagy sebesség, csökkentett erő
- Állandó teljesítmény: Erő × sebesség = állandó
Válaszidő-tényezők:
- Levegő összenyomhatósága: Időkésleltetést hoz létre
- Hangerő hatások: Nagyobb térfogat lassabb reakció
- Áramlási korlátozások: A válaszadási sebesség korlátozása
- Vezérlőszelep reakció: Befolyásolja a rendszer dinamikáját
Milyen energiaátviteli mechanizmusok vannak a pneumatikus rendszerekben?
A pneumatikus rendszerekben az energiaátvitel többféle mechanizmust foglal magában, amelyek a sűrített levegő energiáját a forrástól a felhasználási pontig szállítják, miközben minimalizálják a veszteségeket.
A pneumatikus energiaátvitel a csőhálózatokon keresztül történő nyomásátvitelt, a szelepeken és szerelvényeken keresztül történő áramlásszabályozást, valamint a folyadékmechanikai és termodinamikai elvek által szabályozott energiatárolást használja.
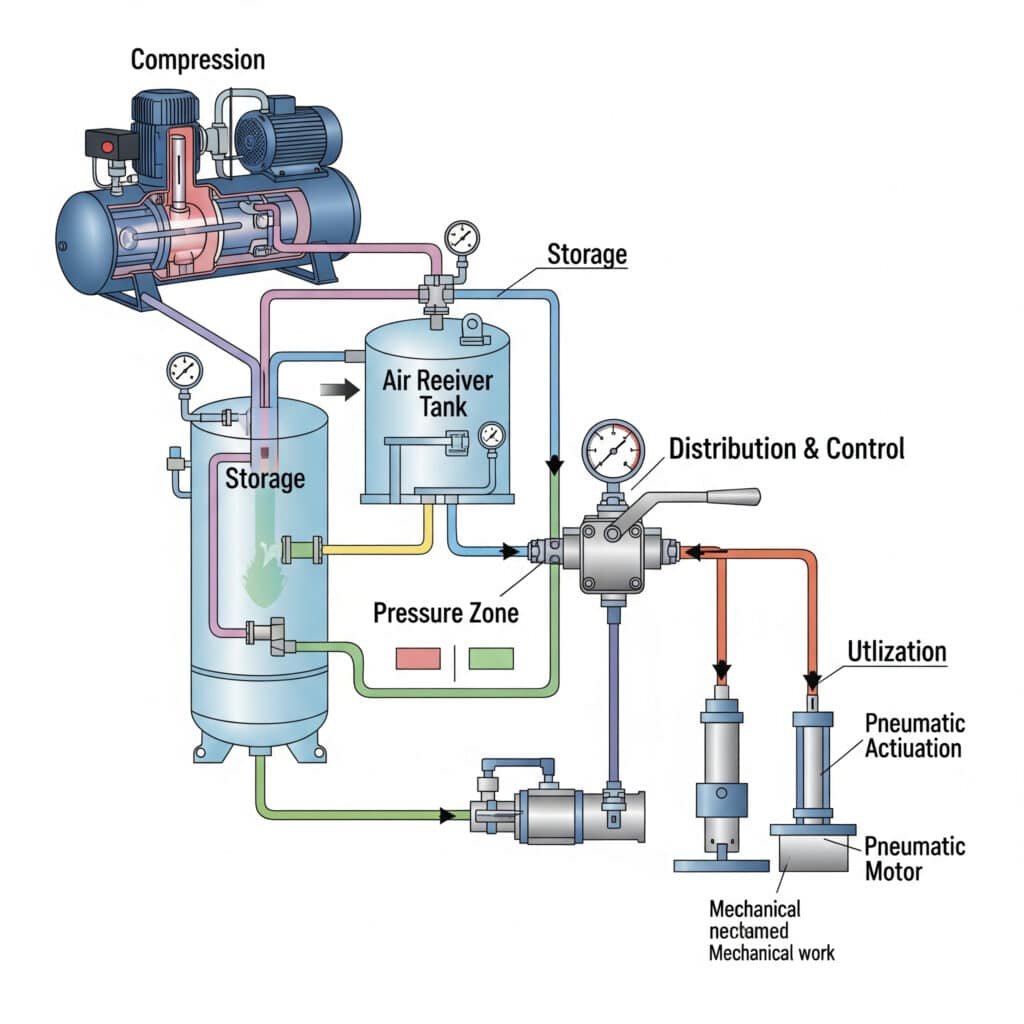
Nyomás átvitel elmélete
A sűrített levegő energiája a pneumatikus rendszerekben nyomáshullámok révén terjed, amelyek hangsebességgel terjednek a légközegben.
Nyomáshullámok terjedése:
Hullámsebesség = √(γRT) = √(γP/ρ)
Hol:
- γ = fajlagos hőhányad (levegő esetében 1,4)
- R = gázállandó
- T = abszolút hőmérséklet
- P = nyomás
- ρ = A levegő sűrűsége
Nyomásátviteli jellemzők:
- Hullámsebesség: Körülbelül 1,100 ft/s levegőben, standard körülmények között.
- Nyomáskiegyenlítés: Gyorsan az összes csatlakoztatott rendszerben
- Távolsági hatások: Minimális a tipikus pneumatikus rendszereknél
- Frekvenciaválasz: Nagyfrekvenciás nyomásváltozások csillapítása
Áramlás alapú energiaátvitel
A pneumatikus rendszereken keresztül történő energiaátvitel a sűrített levegőt a működtető elemekhez és alkatrészekhez juttató levegőáramlási sebességtől függ.
Tömegáramlás energiaátvitel:
Energiaáramlás = ṁ × h
Hol:
- ṁ = Tömegáramlás
- h = a sűrített levegő fajlagos entalpiája
Térfogatáramlási megfontolások:
Q_tényleges = Q_standard × (P_standard/P_tényleges) × (T_tényleges/T_standard)
Flow Energy Relationships:
- Nagy áramlás: Gyors energiaszállítás, gyors reagálás
- Alacsony áramlás: Lassú energiaszállítás, késleltetett válasz
- Áramlási korlátozások: Csökkenti az energiaátvitel hatékonyságát
- Áramlásszabályozás: Szabályozza az energiaszállítási sebességet
Az elosztórendszer energiaveszteségei
A pneumatikus elosztórendszerekben energiaveszteségek keletkeznek, amelyek csökkentik a rendszer hatékonyságát és teljesítményét.
Jelentősebb veszteségforrások:
| Veszteség típusa | Ok | Tipikus veszteség | Enyhítés |
|---|---|---|---|
| Súrlódási veszteségek | Csőfali súrlódás | 2-10 PSI | Megfelelő csőméretezés |
| Szerelési veszteségek | Áramlási zavarok | 1-5 PSI | Minimális szerelvények |
| Szivárgási veszteségek | Rendszerszivárgások | 10-40% | Rendszeres karbantartás |
| Nyomás cseppek | Áramláskorlátozások | 5-15 PSI | A korlátozások megszüntetése |
Nyomáscsökkenés számítása:
ΔP = f × (L/D) × (ρV²/2)
Hol:
- f = Súrlódási tényező
- L = A cső hossza
- D = csőátmérő
- ρ = A levegő sűrűsége
- V = A levegő sebessége
Energiatárolás és -visszanyerés
A pneumatikus rendszerek a hatékonyság és a teljesítmény javítása érdekében energiatárolási és -visszanyerési mechanizmusokat használnak.
Sűrített levegő tárolása:
Tárolt energia = P × V × ln(P/P₀)
Tárolási előnyök:
- Csúcskereslet: Kezelje az ideiglenesen magas keresletet
- Nyomás stabilitás: Fenntartani az egyenletes nyomást
- Energia puffer: A kereslet ingadozásának kiegyenlítése
- Rendszervédelem: A nyomásingadozások megelőzése
Energia-visszanyerési lehetőségek:
- Kipufogógáz visszanyerése: A tágulási energia befogása
- Hővisszanyerés: Használja ki a tömörítési hőt
- Nyomásvisszanyerés: Részlegesen kitágított levegő újrafelhasználása
- Regeneratív rendszerek: Többlépcsős energia-visszanyerés
Vezérlőrendszer Energiagazdálkodás
A pneumatikus vezérlőrendszerek a teljesítmény optimalizálása és a fogyasztás minimalizálása érdekében kezelik az energiaátvitelt.
Ellenőrzési stratégiák:
- Nyomásszabályozás: Az optimális nyomásszintek fenntartása
- Áramlásszabályozás: A kínálat és a kereslet összehangolása
- Szekvenáló vezérlés: Több működtető koordinálása
- Energiafigyelés: A fogyasztás nyomon követése és optimalizálása
Haladó irányítási technikák:
- Változó nyomás: Állítsa be a nyomást a terhelési követelményekhez
- Keresletalapú ellenőrzés: Csak akkor szolgáltat levegőt, ha szükséges
- Terhelésérzékelés: A rendszer beállítása a tényleges kereslet alapján
- Előrejelző vezérlés: Az energiaszükséglet előrejelzése
Hogyan alkalmazható a pneumatika elmélete az ipari rendszerek tervezésénél?
A pneumatika elmélete tudományos alapot nyújt a hatékony, megbízható ipari pneumatikus rendszerek tervezéséhez, amelyek megfelelnek a teljesítménykövetelményeknek, miközben minimalizálják az energiafogyasztást és az üzemeltetési költségeket.
Az ipari pneumatikus rendszerek tervezése a termodinamikai elveket, a folyadékmechanikát, a vezérléselméletet és a gépészmérnöki ismereteket alkalmazza a gyártási, automatizálási és folyamatirányítási alkalmazásokhoz optimalizált sűrített levegős rendszerek létrehozásához.
Rendszertervezési módszertan
A pneumatikus rendszerek tervezése szisztematikus módszertant követ, amely az elméleti alapelveket a gyakorlati követelményekre alkalmazza.
A tervezési folyamat lépései:
- Követelményelemzés: Teljesítményspecifikációk meghatározása
- Elméleti számítások: Alkalmazza a pneumatikai elveket
- Komponens kiválasztása: Válassza ki az optimális alkatrészeket
- Rendszerintegráció: Koordinált komponensek kölcsönhatása
- Teljesítmény optimalizálás: Az energiafogyasztás minimalizálása
- Biztonsági elemzés: A biztonságos működés biztosítása
Tervezési kritériumok megfontolások:
| Tervezési tényező | Elméleti alap | Gyakorlati alkalmazás |
|---|---|---|
| Erőkövetelmények | F = P × A | A működtető méretezése |
| Sebesség követelmények | Áramlási sebesség számítások | Szelepek és csövek méretezése |
| Energiahatékonyság | Termodinamikai elemzés | Komponens optimalizálás |
| Válaszidő | Dinamikus elemzés | Vezérlőrendszer tervezése |
| Megbízhatóság | Hibamód-elemzés | Komponens kiválasztása |
Nyomásszint optimalizálás
Az optimális rendszernyomás egyensúlyt teremt a teljesítménykövetelmények, az energiahatékonyság és az alkatrészköltségek között.
Nyomáskiválasztás elmélete:
Optimális nyomás = f(erőigény, energiaköltségek, alkatrészköltségek)
Nyomásszint-elemzés:
- Alacsony nyomás (50-80 PSI): Alacsonyabb energiaköltségek, nagyobb alkatrészek
- Közepes nyomás (80-120 PSI): Kiegyensúlyozott teljesítmény és hatékonyság
- Nagy nyomás (120-200 PSI): Kompakt alkatrészek, magasabb energiaköltségek
A nyomás energiahatása:
Teljesítmény ∝ P^0.286 (izotermikus tömörítés esetén)
20% nyomásnövekedés = 5,4% teljesítménynövekedés
Komponensek méretezése és kiválasztása
Az elméleti számítások meghatározzák a rendszer teljesítménye és hatékonysága szempontjából optimális alkatrészméreteket.
Működtetőelemek méretezése:
Szükséges nyomás = (terhelési erő + biztonsági tényező) / effektív terület
Szelep méretezése:
Cv = Q × √(ρ/ΔP)
Hol:
- Cv = Szelep áramlási együtthatója
- Q = Áramlási sebesség
- ρ = A levegő sűrűsége
- ΔP = nyomásesés
Csőméret-optimalizálás:
Gazdasági átmérő = K × (Q/v)^0,4
Ahol K az energiaköltségektől és a csőköltségektől függ.
Rendszerintegrációs elmélet
A pneumatikus rendszerintegráció az alkatrészek működésének összehangolására a vezérléselméletet és a rendszerdinamikát alkalmazza.
Integrációs elvek:
- Nyomás illesztés: Az alkatrészek kompatibilis nyomáson működnek
- Flow Matching: A kínálati kapacitás megfelel a keresletnek
- Válaszillesztés: A rendszer időzítése optimalizálva
- Ellenőrzési integráció: Koordinált rendszerüzemeltetés
Rendszerdinamika:
Transzferfüggvény5 = Kimenet/Bemenet = K/(τs + 1)
Hol:
- K = Rendszererősítés
- τ = időállandó
- s = Laplace-változó
Energiahatékonysági optimalizálás
Az elméleti elemzés meghatározza a pneumatikus rendszerek energiahatékonyságának javítási lehetőségeit.
Hatékonyság-optimalizálási stratégiák:
| Stratégia | Elméleti alap | Potenciális megtakarítások |
|---|---|---|
| Nyomás optimalizálás | Termodinamikai elemzés | 10-30% |
| Szivárgás megszüntetése | Tömegmegmegőrzés | 20-40% |
| Komponensek méretezése | Áramlás optimalizálása | 5-15% |
| Hővisszanyerés | Energiatakarékosság | 10-20% |
| Vezérlés optimalizálása | Rendszerdinamika | 5-25% |
Életciklusköltség-elemzés:
Teljes költség = kezdeti költség + működési költség × jelenérték-tényező
Ahol az üzemeltetési költség magában foglalja a rendszer élettartama alatti energiafogyasztást.
Nemrégiben egy Michael O'Brien nevű ausztrál gyártómérnökkel dolgoztam együtt, akinek a pneumatikus rendszer újratervezési projektje elméleti validálásra szorult. A megfelelő pneumatikai elméleti alapelvek alkalmazásával optimalizáltuk a rendszer kialakítását, hogy 52% energiacsökkentést érjünk el, miközben 35%-tel javítottuk a teljesítményt és 40%-tel csökkentettük a karbantartási költségeket.
Biztonsági elmélet alkalmazása
A pneumatikus biztonságelmélet biztosítja a rendszerek biztonságos működését a teljesítmény és a hatékonyság fenntartása mellett.
Biztonsági elemzési módszerek:
- Veszélyelemzés: A potenciális biztonsági kockázatok azonosítása
- Kockázatértékelés: A valószínűség és a következmények számszerűsítése
- Biztonsági rendszer tervezése: Védőintézkedések végrehajtása
- Hibamód-elemzés: Az alkatrészek meghibásodásának előrejelzése
Biztonsági tervezési elvek:
- Meghibásodásbiztos tervezés: A rendszer biztonságos állapotba kerül
- Redundancia: Többszörös védelmi rendszerek
- Energia elszigetelés: A tárolt energia eltávolításának képessége
- Nyomáscsökkentés: Túlnyomásos körülmények megelőzése
Következtetés
A pneumatika elmélete magában foglalja a termodinamikai energiaátalakítást, a folyadékmechanikát és a sűrített levegős rendszereket szabályozó vezérlési elveket, amelyek tudományos alapot biztosítanak a hatékony és megbízható ipari automatizálási és gyártási rendszerek tervezéséhez.
GYIK a pneumatikus elméletről
Mi a pneumatikus rendszerek alapvető elmélete?
A pneumatika elmélete a sűrített levegő energiaátalakításán alapul, ahol a légköri levegőt a potenciális energia tárolása érdekében összenyomják, az elosztórendszereken keresztül továbbítják, és a termodinamikai és áramlástani elvek felhasználásával működtetőkön keresztül mechanikai munkává alakítják.
Hogyan alkalmazható a termodinamika a pneumatikus rendszerekre?
A termodinamika a pneumatikus rendszerek energiaátalakítását az első törvény (az energia megőrzése) és a második törvény (entrópia/határértékek) segítségével szabályozza, meghatározva a kompressziós munkát, a hőtermelést és a maximális elméleti hatásfokot.
Melyek a legfontosabb energiaátalakítási mechanizmusok a pneumatikában?
A pneumatikus energiaátalakítás a következőket foglalja magában: elektromosból mechanikusba (kompresszor meghajtása), mechanikusból pneumatikusba (levegő sűrítése), pneumatikus tárolás (sűrített levegő), pneumatikus átvitel (elosztás) és pneumatikusból mechanikusba (működtető munkakimenet).
Hogyan alakítják át a pneumatikus alkatrészek a levegő energiáját munkává?
A pneumatikus alkatrészek a levegő energiáját lineáris erő esetén nyomás-térfogat összefüggésekkel (F = P × A), mozgás esetén nyomás-térfogat kiterjedéssel, forgó mozgáshoz pedig speciális mechanizmusokkal alakítják át, amelyek hatékonyságát a kialakítás és a működési feltételek határozzák meg.
Milyen tényezők befolyásolják a pneumatikus rendszer hatékonyságát?
A rendszer hatásfokát a sűrítési veszteségek (10-20%), az elosztási veszteségek (5-20%), a működtetőegységek veszteségei (10-20%), a hőtermelés (10-20%) és a vezérlési veszteségek (5-15%) befolyásolják, így a teljes hatásfok jellemzően 20-40%.
Hogyan irányítja a pneumatika elmélete az ipari rendszerek tervezését?
A pneumatikai elmélet a rendszertervezés tudományos alapját termodinamikai számítások, áramlástani elemzés, alkatrészméretezés, nyomásoptimalizálás és energiahatékonysági elemzés révén biztosítja az optimális ipari sűrítettlevegő-rendszerek létrehozásához.
-
Áttekintést nyújt a termodinamika alapelveiről, beleértve a zéró, első, második és harmadik törvényt, amelyek az energiát, a hőt, a munkát és az entrópiát szabályozzák a fizikai rendszerekben. ↩
-
Részletes magyarázatot ad az ideális gáztörvényre (PV=nRT), az alapvető állapotegyenletre, amely megközelíti a legtöbb gáz viselkedését különböző körülmények között, és összefüggésbe hozza a nyomást, a térfogatot, a hőmérsékletet és a gáz mennyiségét. ↩
-
Leírja és összehasonlítja az izotermikus (állandó hőmérsékletű), az adiabatikus (nincs hőátadás) és a polytropikus (hőátadást lehetővé tevő) kulcsfontosságú termodinamikai folyamatokat, amelyek kulcsfontosságúak a valós gázkompresszió és -tágulás modellezéséhez. ↩
-
Ismerteti a kompresszibilitási tényező (Z) fogalmát, amely egy korrekciós tényező, amely egy valós gáz ideális gáz viselkedésétől való eltérését írja le, és amelyet az ideális gáztörvény módosítására használnak, hogy nagyobb pontosságot biztosítsanak a valós számítások során. ↩
-
Megadja az átviteli függvény definícióját, amely egy olyan matematikai ábrázolás az irányításelméletben, amely egy lineáris időinvariáns rendszer bemenete és kimenete közötti kapcsolatot modellezi a Laplace-tartományban. ↩


