A nyomásmérések még a tapasztalt mérnököket is összezavarják. Számtalan olyan pneumatikus rendszerrel foglalkoztam már, ahol a helytelen nyomásreferenciák teljesítményproblémákat okoztak. Az abszolút nyomás megértése megelőzi a költséges számítási hibákat és a rendszerhibákat.
Az abszolút nyomás (ABS-nyomás) a tökéletes vákuumhoz viszonyított nyomást méri, beleértve a légköri nyomást is a mérésbe. Ez egyenlő a nyomás és a légköri nyomás (14,7 PSI tengerszinten), így a pneumatikus alkatrészekre ható valódi teljes nyomást adja meg.
A múlt héten segítettem Thomasnak, egy holland gyártó cég tervezőmérnökének, hogy megoldja a magassággal kapcsolatos teljesítményproblémákat az ő rúd nélküli pneumatikus henger1 rendszer. Számításai tökéletesen működtek a tengerszinten, de a hegyi létesítményükben nem sikerült. A probléma nem a berendezés meghibásodása volt - hanem az abszolút nyomás téves értelmezése.
Tartalomjegyzék
- Mi az abszolút nyomás és miben különbözik a mérőnyomástól?
- Miért kritikus az abszolút nyomás a pneumatikus számításoknál?
- Hogyan befolyásolja a magasság az abszolút nyomást a pneumatikus rendszerekben?
- Melyek az abszolút nyomás általános alkalmazásai ipari környezetben?
- Hogyan lehet átváltani a különböző nyomásmérések között?
- Milyen hibákat követnek el a mérnökök az abszolút nyomásszámításokkal?
Mi az abszolút nyomás és miben különbözik a mérőnyomástól?
Az abszolút nyomás a rendszerre ható teljes nyomást jelenti, egy tökéletes vákuum referenciapontból mérve. Ez a mérés tartalmazza a légköri nyomás hatásait, amelyeket a mérőnyomás figyelmen kívül hagy.
Az abszolút nyomás egyenlő a nyomás plusz a légköri nyomás. A tengerszinten a légköri nyomás 14,7 PSI, így a 80 PSIG mérőnyomás 94,7 PSIA abszolút nyomásnak felel meg. Ez a különbségtétel kulcsfontosságú a pontos pneumatikus rendszer számításaihoz.

A nyomás referenciapontok megértése
A különböző nyomásmérések különböző referenciapontokat használnak:
| Nyomás típus | Referenciapont | Szimbólum | Tipikus tartomány |
|---|---|---|---|
| Abszolút | Tökéletes vákuum | PSIA | 0 és 1000+ PSIA között |
| Mérőeszköz | Atmoszféra | PSIG | -14,7 és 1000+ PSIG között |
| Differenciális | Két pont között | PSID | Változó |
| Vákuum | Légköri értékek alatt | "Hg | 0 és 29,92 "Hg között |
Abszolút nyomás alapjai
Az abszolút nyomás teljes nyomásképet nyújt. Ez magában foglalja mind az alkalmazott nyomást, mind a rendszert körülvevő légköri nyomást.
Az alapvető kapcsolat a következő:
PSIA = PSIG + légköri nyomás
Normál tengerszint feletti körülmények között:
PSIA = PSIG + 14,7
Mérőnyomás-korlátozások
A nyomásmérések figyelmen kívül hagyják a légköri nyomásváltozásokat. Ez problémákat okoz, amikor a légköri nyomás a magasság vagy az időjárási körülmények miatt változik.
A nyomásmérő a legtöbb ipari alkalmazásban jól működik, mivel a légköri nyomás viszonylag állandó marad a rögzített helyeken. Az abszolút nyomás azonban kritikussá válik a következő esetekben:
- Magassági kompenzációs számítások
- Vákuumrendszer kialakítása
- Gáztörvény alkalmazásai
- Áramlási sebesség számítások
- Hőmérséklet-kompenzáció
Gyakorlati mérési különbségek
Nemrégiben együtt dolgoztam Annával, egy norvég tengeri platform folyamatmérnökével. A pneumatikus számításai tökéletesen működtek a szárazföldön, de meghibásodtak, amikor a berendezés átkerült a tengeri üzembe.
A probléma a légköri nyomás változása volt. Az időjárási rendszerek 1-2 PSI légköri nyomásváltozást okoztak, ami befolyásolta a nyomásmérők leolvasását. Az abszolút nyomásmérésre való áttéréssel kiküszöböltük az időjárással kapcsolatos teljesítményváltozásokat.
Vizuális megértés
Gondoljon úgy az abszolút nyomásra, mintha egy medence aljától (tökéletes vákuum) a vízfelszínig (rendszernyomás) mérné. A mérőnyomás csak a normál vízszinttől (légköri nyomás) a felszínig mér.
Ez az analógia segít megérteni, hogy az abszolút nyomás miért nyújt teljesebb információt a mérnöki számításokhoz.
Miért kritikus az abszolút nyomás a pneumatikus számításoknál?
Az abszolút nyomás képezi a pontos pneumatikus rendszerszámítások alapját. Számos mérnöki képlethez abszolút nyomásértékek szükségesek a helyes eredményekhez.
Az abszolút nyomás elengedhetetlen a pneumatikai számításokhoz, mivel a gáztörvények, az áramlási egyenletek és a termodinamikai összefüggések abszolút nyomásértékeket használnak. Ha ezekben a képletekben a mérőnyomást használjuk, akkor helytelen eredményeket kapunk, ami a rendszer meghibásodásához vezethet.
Gáztörvény alkalmazások
A ideális gáztörvény2 a pontos számításokhoz abszolút nyomás szükséges:
PV = nRT
Hol:
- P = abszolút nyomás
- V = térfogat
- n = a mólok száma
- R = gázállandó
- T = Abszolút hőmérséklet3
A gáztörvény számításaiban a nyomásmérők használata a légköri nyomással arányos hibákat eredményez. Tengerszinten ez a legtöbb számításban 15% hibát okoz.
Áramlási sebesség számítások
A pneumatikus áramlási sebesség képletei abszolút nyomásarányokat igényelnek:
Áramlási sebesség ∝ √(P₁² - P₂²)
Ahol P₁ és P₂ a szűkítés előtti és utáni abszolút nyomás.
Az áramlási számításokban a nyomásmérők használata 20%-t meghaladó hibákat eredményezhet, ami a rendszeralkatrészek alulméretezéséhez vagy túlméretezéséhez vezethet.
Henger erő számítások
Míg az alapvető erőszámítások (F = P × A) mérőnyomással működnek, a haladó alkalmazásokhoz abszolút nyomás szükséges:
Magassági kompenzáció
Az erőkifejtés a magassággal változik a légköri nyomás változása miatt. Az abszolút nyomásszámítások figyelembe veszik ezeket a változásokat.
Hőmérsékleti hatások
A gáztágulási és -összehúzódási számításokhoz abszolút nyomás- és hőmérsékletértékekre van szükség a pontosság érdekében.
Kompresszor teljesítménye
A kompresszorok méretezése és teljesítményszámításai abszolút nyomásarányokat használnak:
Tömörítési arány = P₂(abs) ÷ P₁(abs)
Ez az arány határozza meg a kompresszorfokozat követelményeit és az energiafogyasztást. A nyomásmérők használata helytelen tömörítési arányok4.
Valós világbeli példa
Segítettem Marcusnak, egy svájci precíziós gyártóüzem karbantartási felügyelőjének megoldani a rúd nélküli hengerek következetlen teljesítményét. A létesítménye 3000 láb magasan működött, ahol a légköri nyomás 13,2 PSI a tengerszint feletti 14,7 PSI helyett.
A nyomásmérője 80 PSIG-t mutatott, de az abszolút nyomás csak 93,2 PSIA volt a várt 94,7 PSIA helyett. Ez az 1,5 PSI különbség 1,6%-vel csökkentette a henger erőterhelését, ami pozicionálási pontossági problémákat okozott a precíziós alkalmazásokban.
Számításainak a helyi légköri nyomásra való újrakalibrálásával helyreállítottuk a rendszer megfelelő teljesítményét.
Vákuum alkalmazások
A vákuumrendszerek abszolút nyomásmérést igényelnek, mivel a légköri nyomás alatt a mérőnyomás negatívvá válik:
| Vákuumszint | Nyomásmérő nyomás | Abszolút nyomás |
|---|---|---|
| Durva vákuum | -10 PSIG | 4.7 PSIA |
| Közepes vákuum | -13 PSIG | 1.7 PSIA |
| Magas vákuum | -14,5 PSIG | 0,2 PSIA |
| Tökéletes vákuum | -14,7 PSIG | 0,0 PSIA |
Hogyan befolyásolja a magasság az abszolút nyomást a pneumatikus rendszerekben?
A tengerszint feletti magasság jelentősen befolyásolja a légköri nyomást, ami kihat a pneumatikus rendszer teljesítményére. E hatások megértése megelőzi a teljesítményproblémákat a magasan fekvő létesítményekben.
A légköri nyomás körülbelül 0,5 PSI-vel csökken 1000 lábnyi emelkedésenként. Ez a csökkenés befolyásolja az abszolút nyomásszámításokat, és 1000 láb magassági emelkedésenként 3-4%-vel csökkentheti a pneumatikus hengerek teljesítményét.
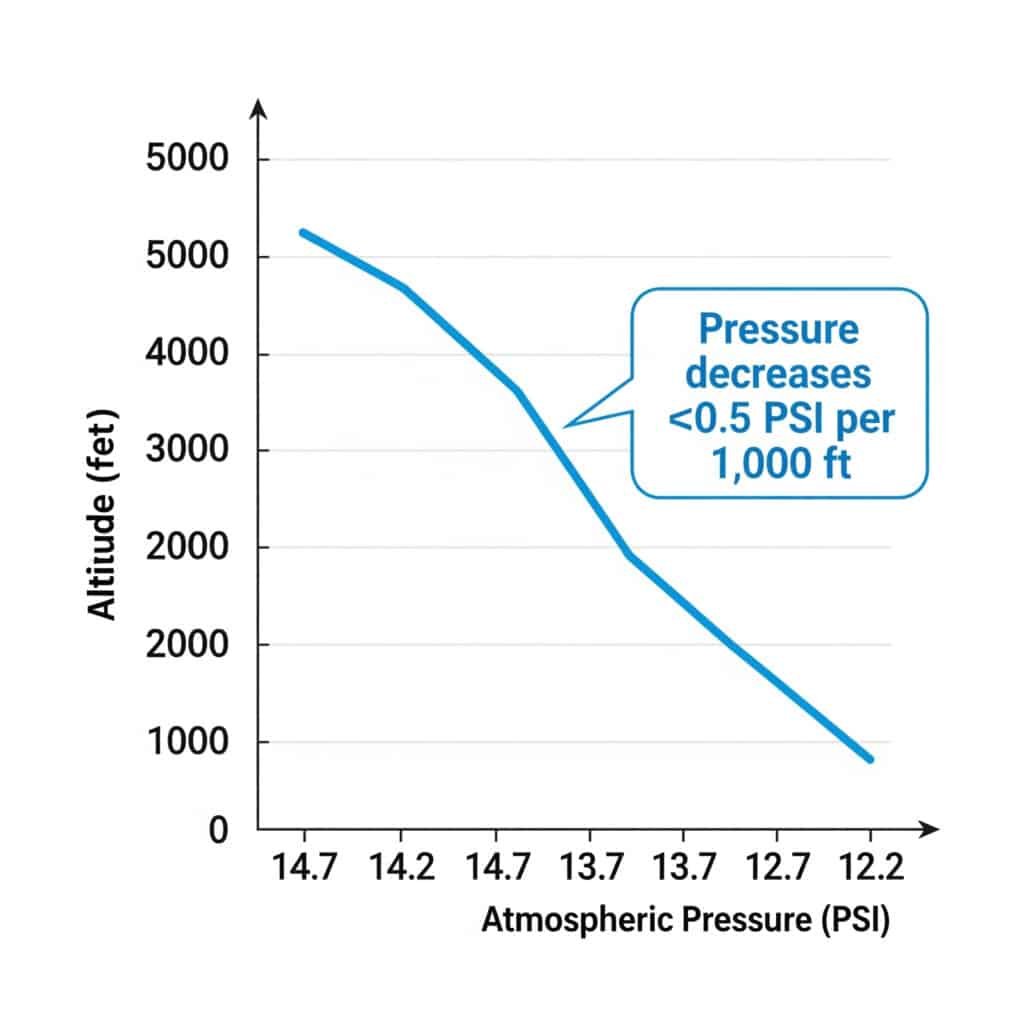
A légköri nyomás és a tengerszint feletti magasság függvénye
A normál légköri nyomás kiszámíthatóan változik a magassággal:
| Magasság (láb) | Légköri nyomás (PSIA) | Nyomáscsökkentés |
|---|---|---|
| Tengerszint | 14.7 | 0% |
| 1,000 | 14.2 | 3.4% |
| 2,000 | 13.7 | 6.8% |
| 5,000 | 12.2 | 17.0% |
| 10,000 | 10.1 | 31.3% |
Erő kimeneti hatás
A csökkentett légköri nyomás befolyásolja a hengererő számításokat, ha abszolút nyomást használunk:
Hatásos nyomás = nyomás + helyi légköri nyomás
Egy 80 PSIG nyomáson működő henger esetében:
- Tengerszint: 80 + 14,7 = 94,7 PSIA
- 5,000 láb: 80 + 12,2 = 92,2 PSIA
- Erőcsökkentés: 2.6%
Magassági kompenzációs stratégiák
A magassági hatások kompenzálására több módszer is létezik:
Nyomás beállítása
Növelje a mérőnyomást az állandó abszolút nyomás fenntartásához:
Szükséges mérőnyomás = cél abszolút nyomás - helyi légköri nyomás
A rendszer újratervezése
A hengerek méretének módosítása a teljesítmény fenntartása érdekében csökkentett abszolút nyomás mellett.
Vezérlőrendszer kompenzáció
Programozza a vezérlőrendszereket a helyi légköri nyomásváltozásokhoz való alkalmazkodásra.
A hőmérséklet és a magasság együttes hatása
A magasság és a hőmérséklet egyaránt befolyásolja a levegő sűrűségét és a rendszer teljesítményét:
Levegő sűrűsége = (abszolút nyomás × molekulatömeg) ÷ (gázkonstans × abszolút hőmérséklet)
A nagyobb magasságokban jellemzően alacsonyabb a hőmérséklet, ami részben ellensúlyozza a légsűrűségre gyakorolt nyomáscsökkentő hatást.
Valós magassági alkalmazás
Carlos projektmenedzserrel dolgoztam együtt, aki pneumatikus rendszereket telepített egy perui bányászati üzemben, 12 000 láb magasan. A tengerszint feletti számításai megfelelő erőt mutattak az anyagmozgatási alkalmazásokhoz.
A telepítés magasságában a légköri nyomás csak 9,3 PSIA volt, szemben a tengerszint feletti 14,7 PSIA-val. Ez a 37% légköri nyomáscsökkenés jelentősen befolyásolta a rendszer teljesítményét.
Mi kompenzáltuk:
- Az üzemi nyomás növelése 80-ról 95 PSIG-re
- A kritikus hengerek 15%-vel történő növelése
- Nyomásfokozók hozzáadása nagy erőkifejtéshez
A módosított rendszer a szélsőséges magassági körülmények ellenére is biztosította a szükséges teljesítményt.
Időjárási hatások a magasságban
A magasan fekvő helyeken az időjárás miatt nagyobb légköri nyomásingadozás tapasztalható:
A tengerszint változása
- Nagy nyomás: 15,2 PSIA (+0,5 PSI)
- Alacsony nyomás: 14,2 PSIA (-0,5 PSI)
- Teljes tartomány: 1.0 PSI
Nagy magassági variációk (10,000 láb)
- Nagy nyomás: 10,6 PSIA (+0,5 PSI)
- Alacsony nyomás: 9.6 PSIA (-0.5 PSI)
- Teljes tartomány: 1,0 PSI (10% alapnyomás)
Melyek az abszolút nyomás általános alkalmazásai ipari környezetben?
Az abszolút nyomásmérés számos ipari alkalmazásban elengedhetetlen, ahol a pontos nyomásviszonyok meghatározzák a rendszer teljesítményét és biztonságát.
Az abszolút nyomás gyakori alkalmazásai közé tartoznak a vákuumrendszerek, gázáramlási számítások, kompresszorok méretezése, magassági kompenzáció és termodinamikai folyamatok. Ezek az alkalmazások abszolút nyomást igényelnek, mivel a nyomásmérések nem nyújtanak teljes körű információt.
Vákuum rendszer tervezése
A vákuumos alkalmazások abszolút nyomásmérést igényelnek, mivel a mérőnyomás negatívvá válik a légköri viszonyok alatt:
Vákuumszivattyú méretezése
A vákuumszivattyú teljesítménye az abszolút nyomásarányoktól függ:
Szivattyúzási sebesség = Térfogatáram ÷ (P₁ - P₂)
Ahol P₁ és P₂ a szivattyú bemeneti és kimeneti abszolút nyomása.
Vákuumszint specifikációk
Az ipari vákuumszintek abszolút nyomásmérést használnak:
| Alkalmazás | Vákuumszint (PSIA) | Tipikus használat |
|---|---|---|
| Anyagmozgatás | 10-12 | Szívókupakok, szállítószalagok |
| Csomagolás | 5-8 | Vákuumcsomagolás |
| Folyamatos iparágak | 1-3 | Desztilláció, szárítás |
| Laboratórium | 0.1-0.5 | Kutatási alkalmazások |
Gázáramlás mérése
A pontos gázáramlási számításokhoz abszolút nyomásértékekre van szükség:
Fojtott áramlási feltételek
A gázáramlás elszorul, amikor a nyomás a kritikus nyomás alá csökken:
Kritikus nyomásarány = 0,528 (levegő esetében)
Ehhez a számításhoz abszolút nyomás szükséges az áramlási korlátozások meghatározásához.
Tömegáramlási számítások
A tömegáram függ az abszolút nyomástól és a hőmérséklettől:
Tömegáram = (abszolút nyomás × terület × sebesség) ÷ (gázkonstans × abszolút hőmérséklet)
Kompresszor alkalmazások
A kompresszorok méretezése és teljesítménye az abszolút nyomásarányokat használja:
Kompressziós arány számítások
Kompressziós arány = Kiáramlási nyomás (abs) ÷ szívási nyomás (abs)
Ez az arány határozza meg:
- A szükséges tömörítési fokozatok száma
- Energiafogyasztás
- Kiürítési hőmérséklet
- Hatékonysági jellemzők
Kompresszor teljesítménytérképek
A gyártó teljesítménytérképei abszolút nyomásviszonyokat használnak a pontos kiválasztáshoz és működéshez.
Folyamatszabályozási alkalmazások
Számos folyamatirányító rendszerben abszolút nyomásmérésre van szükség:
Sűrűség számítások
Gázsűrűség-számítások áramlásméréshez és -szabályozáshoz:
Sűrűség = (abszolút nyomás × molekulatömeg) ÷ (gázállandó × abszolút hőmérséklet)
Hőátadási számítások
A hőcserélők és technológiai berendezések termodinamikai számításai abszolút nyomás- és hőmérsékleti értékeket használnak.
Valós világbeli folyamat alkalmazása
Nemrégiben segítettem Elenának, egy német vegyi üzem folyamatmérnökének, hogy pneumatikus szállítás5 rendszertervezés. Az ő rendszere sűrített levegővel szállította a műanyag pelleteket a magasan fekvő csővezetékeken keresztül.
A szállítási számításokhoz abszolút nyomásértékek meghatározására volt szükség:
- A levegő sűrűsége a csővezeték különböző magasságaiban
- Nyomásveszteség számítások függőleges szakaszokon keresztül
- Anyagsebességre vonatkozó követelmények
- A rendszer kapacitásának korlátai
A mérőnyomás használata 15-20% hibákat eredményezett volna a szállítási kapacitás számításaiban, ami alulméretezett berendezésekhez és gyenge teljesítményhez vezetett volna.
Minőségellenőrzési alkalmazások
A precíziós gyártás gyakran igényel abszolút nyomásmérést:
Szivárgásvizsgálat
Az abszolút nyomásmérés pontosabb szivárgásérzékelést biztosít:
Szivárgási sebesség = Térfogat × nyomásesés ÷ idő
Az abszolút nyomás használata kiküszöböli a légköri nyomás ingadozásait, amelyek befolyásolják a mérőnyomás leolvasását.
Kalibrációs szabványok
A nyomáskalibráló etalonok abszolút nyomásreferenciákat használnak a pontosság és a nyomon követhetőség érdekében.
Hogyan lehet átváltani a különböző nyomásmérések között?
A különböző mérőrendszerek közötti nyomásátváltáshoz meg kell ismerni a referenciapontokat és az átváltási tényezőket. A pontos átváltások megakadályozzák a számítási hibákat a nemzetközi projekteknél.
A nyomásátváltások az abszolút és a manométeres mérések közötti váltáskor a légköri nyomás hozzáadásával vagy kivonásával, valamint az egységátváltási tényezők alkalmazásával történnek. A gyakori átváltások közé tartozik a PSIA barra, a PSIG kPa-ra és a vákuum mérések abszolút nyomásra történő átváltása.
Alapvető átváltási képletek
A nyomástípusok közötti alapvető kapcsolat:
Abszolút nyomás = mérőnyomás + légköri nyomás
Manométernyomás = abszolút nyomás - légköri nyomás
Vákuum = légköri nyomás - abszolút nyomás
Egység-átváltási tényezők
Gyakori nyomásegység-átváltások:
| From | To | Multiply By |
|——|—-|———–|
| PSI | bar | 0.06895 |
| bar | PSI | 14.504 |
| PSI | kPa | 6.895 |
| kPa | PSI | 0.1450 |
| PSI | "Hg | 2.036 |
| "Hg | PSI | 0.4912 |
Légköri nyomás szabványok
Átváltásokhoz használt szabványos légköri nyomásértékek:
| Helyszín/Standard | Nyomás Érték |
|---|---|
| Tengerszint szabvány | 14,696 PSIA, 1,01325 bar |
| Mérnöki szabvány | 14,7 PSIA, 1,013 bar |
| Metrikus szabvány | 101.325 kPa, 760 mmHg |
Átalakítási példák
PSIG to PSIA történő átváltás.
80 PSIG - PSIA tengerszinten:
80 PSIG + 14,7 = 94,7 PSIA
Barométer to Bar abszolút to Bar abszolút
5 barg to bara tengerszinten:
5 barg + 1.013 = 6.013 bara
Vákuum to Abszolút nyomás
25 "Hg vákuum a PSIA-hoz:
14,7 - (25 × 0,4912) = 2,42 PSIA
Nemzetközi egységgel kapcsolatos megfontolások
A különböző országok különböző nyomásegységeket használnak:
| Régió | Közös egységek | Standard légköri |
|---|---|---|
| USA | PSIG, PSIA | 14,7 PSI |
| Európa | bar, kPa | 1,013 bar |
| Ázsia | MPa, kgf/cm² | 1,033 kgf/cm² |
| Tudományos | Pa, kPa | 101,325 kPa |
Átváltási pontossági megfontolások
Az átváltás pontossága a légköri nyomásra vonatkozó feltételezésektől függ:
Szabványos vs. tényleges feltételek
- Standard: 14,7 PSI légköri nyomást használ.
- Tényleges: A helyi légköri nyomást használja
- Hiba: A helytől és az időjárástól függően 1-3% lehet.
Hőmérsékleti hatások
A légköri nyomás a hőmérséklet és az időjárási viszonyok függvényében változik. A pontos átváltásokhoz a szabványos értékek helyett a tényleges helyi légköri nyomást használja.
Digitális konverziós eszközök
A modern nyomásmérő műszerek gyakran automatikus egységátváltást biztosítanak. A kézi átváltás elveinek megértése azonban segít a digitális leolvasások ellenőrzésében és az átváltási hibák elhárításában.
Gyakorlati átalakítás alkalmazása
Jean-Pierre-rel, egy francia autóipari beszállító projektmérnökével dolgoztam egy globális projekt pneumatikus rendszerének specifikációin. Az európai specifikációi bar nyomást használtak, de az észak-amerikai telepítés PSIG értékeket követelt meg.
Az átalakítás folyamata:
- Európai specifikáció: 6 barg üzemi nyomás
- Abszolútra konvertálás: 6 + 1,013 = 7,013 bara
- Egységek átalakítása: 7,013 × 14,504 = 101,7 PSIA
- Átalakítás to Gauge: 101,7 - 14,7 = 87,0 PSIG
Ez a szisztematikus megközelítés biztosította a különböző mérőrendszerek pontos nyomásmeghatározását, és megelőzte a berendezések méretezési hibáit.
Milyen hibákat követnek el a mérnökök az abszolút nyomásszámításokkal?
Az abszolút nyomásszámítási hibák gyakoriak, és jelentős rendszerteljesítmény-problémákhoz vezethetnek. E hibák megértése segít megelőzni a költséges tervezési és üzemeltetési problémákat.
Az abszolút nyomás gyakori tévedései közé tartozik a mérőnyomás használata a gáztörvény számításaiban, a légköri nyomásváltozások figyelmen kívül hagyása, a helytelen mértékegység-átváltások és a vákuummérések félreértése. Ezek a hibák jellemzően 10-30% számítási pontatlanságokat és rendszerteljesítmény-problémákat okoznak.
A mérőnyomás használata a gáztörvény számításaiban
A leggyakoribb hiba, hogy abszolút nyomást igénylő képletekben a mérőnyomást használják:
Helytelen gáztörvény alkalmazása
Téves: PV = nRT mérőnyomással
Helyes: PV = nRT abszolút nyomás alkalmazásával
Ez a hiba a légköri nyomással arányos számítási hibákat okoz - tengerszint feletti körülmények között körülbelül 15%.
A légköri nyomásváltozások figyelmen kívül hagyása
Sok mérnök helytől és körülményektől függetlenül állandó 14,7 PSI légköri nyomást feltételez:
Helyszínváltozatok
- Tengerszint: 14.7 PSIA
- Denver (5,280 ft): 12.2 PSIA
- Hiba: 17%, ha a denveri tengerszint feletti értéket használja.
Időjárási változások
- Nagynyomású rendszer: 15.2 PSIA
- Alacsony nyomású rendszer: 14.2 PSIA
- Variáció: ±3,4% a szabványtól eltérően
Hibás egység-átváltások
Az abszolút és a manométeres nyomásegységek keverése jelentős hibákat okoz:
Gyakori konverziós hibák
- 14,7 hozzáadása a bar-mérő leolvasásához (1,013-at kell hozzáadni)
- 14,7 PSI használata a nem tengerparti helyeken
- Elfelejtette az abszolút és a mértékegységek közötti átváltást az egységek váltásakor
Vákuum mérési zűrzavar
A vákuummérések gyakran összezavarják a mérnököket, mert a légköri nyomás alatti nyomást jelentenek:
Vákuumnyomás összefüggések
- 29 "Hg vákuum = 0,76 PSIA (nem -29 PSIA)
- Tökéletes vákuum = 0 PSIA abszolút
- Légköri nyomás = Maximális lehetséges vákuum "Hg-ban
Nemrégiben segítettem Robertónak, egy olasz csomagolóipari vállalat tervezőmérnökének a vákuumrendszer teljesítményével kapcsolatos problémák megoldásában. Számításai megfelelő vákuumszivattyú kapacitást mutattak, de a rendszer nem tudta elérni a szükséges vákuumszintet.
A probléma a vákuummérés zavara volt. Roberto a szivattyú szükségleteit -25 PSIG helyett a helyes 1,4 PSIA abszolút nyomás alapján számolta ki. Ez a hiba a szivattyút a tényleges kapacitásnál 18-szor nagyobb teljesítményűnek tüntette fel.
Hőmérséklet-kompenzációs hibák
Az abszolút nyomásszámítások gyakran figyelmen kívül hagyják a hőmérsékleti hatásokat:
Gáztörvény Hőmérsékleti követelmények
A gáztörvény számításaihoz abszolút hőmérsékletre (Rankine vagy Kelvin) van szükség:
- Fahrenheit to Rankine történő átváltás.: °R = °F + 459,67
- Celsius to Kelvin történő átváltás.: K = °C + 273,15
A Fahrenheit vagy Celsius hőmérséklet használata a gáztörvény számításaiban jelentős hibákat eredményez.
Magassági kompenzációs felügyelet
A mérnökök gyakran a tengerszint feletti légköri nyomást használják a nagy magasságú létesítményekhez:
Magassági nyomáshibák
10,000 láb magasságban:
- Tényleges légköri: 10.1 PSIA
- Tengerszint feltételezés: 14.7 PSIA
- Hiba: 45% abszolút nyomás túlbecslése
Kompresszor arány számítási hibák
A sűrítési arány számításaihoz abszolút nyomás szükséges, de a mérnökök gyakran mérőnyomást használnak:
Helytelen sűrítési arány
80 PSIG nyomás, atmoszférikus szívás esetén:
- Téves: 80 ÷ 0 = meghatározatlan
- Helyes: 94.7 ÷ 14.7 = 6.44:1
Áramlási számítási hibák
A nyomáskülönbségeket használó áramlási számításokhoz abszolút nyomásértékekre van szükség:
Fojtott áramlási hibák
Kritikus nyomásarány számítások:
- Téves: A nyomásarányok használata
- Helyes: Abszolút nyomásarányok használata
- Hatás: 15-20%-vel túlbecsülheti az áramlási kapacitást.
Biztonsági rendszer tervezési hibái
A biztonsági túlnyomáscsökkentő szelepek méretezéséhez abszolút nyomásszámításokra van szükség:
A nyomáscsökkentő szelep méretezése
A nyomáscsökkentő szelep kapacitása az abszolút nyomásviszonyoktól függ. A mért nyomásértékek használata alulméretezett túlnyomásszelepeket és biztonsági kockázatokat eredményezhet.
Megelőzési stratégiák
Kerülje el az abszolút nyomásszámítási hibákat:
Szisztematikus megközelítés
- A szükséges nyomástípus azonosítása: Határozza meg, hogy a számításhoz abszolút vagy mérőnyomás szükséges-e
- Helyes légköri nyomás használata: A helyi légköri nyomást alkalmazza, nem a szabványos tengerszintet.
- Az egység konzisztenciájának ellenőrzése: Biztosítsa, hogy minden nyomás ugyanazt az egységrendszert használja
- Kétszeresen ellenőrizze a konverziókat: Az átváltási tényezők és referenciapontok ellenőrzése
Dokumentációs szabványok
- A nyomástípusok egyértelmű címkézése: Mindig adja meg a PSIA, PSIG, bara, barg értékeket.
- Állami referenciafeltételek: Dokumentálja a légköri nyomásra vonatkozó feltételezéseket
- Átváltási táblázatok beépítése: Adjon referencia-átváltási tényezőket
Következtetés
Az abszolút nyomás a pontos pneumatikus rendszer számításaihoz elengedhetetlenül szükséges teljes nyomásképet nyújt. Az abszolút nyomás elveinek megértése megelőzi a gyakori számítási hibákat, és biztosítja a rúd nélküli hengeres rendszer megbízható teljesítményét a különböző üzemi körülmények között.
GYIK az abszolút nyomásról a pneumatikus rendszerekben
Mi a különbség az abszolút nyomás és a mérőnyomás között?
Az abszolút nyomás a tökéletes vákuumból származó teljes nyomást, míg a mérőnyomás a légköri nyomás feletti nyomást méri. Az abszolút nyomás egyenlő a nyomásmérő nyomása és a légköri nyomás (14,7 PSI tengerszinten).
Miért van szükség a pneumatikus számításokhoz abszolút nyomásra?
A gáztörvények, az áramlási egyenletek és a termodinamikai számítások abszolút nyomást igényelnek, mivel olyan nyomásarányokat és összefüggéseket tartalmaznak, amelyek teljes nyomásértékeket igényelnek. A mérőnyomás használata 10-30% számítási hibát eredményez.
Hogyan befolyásolja a magasság az abszolút nyomást a pneumatikus rendszerekben?
A légköri nyomás körülbelül 0,5 PSI-vel csökken 1000 lábnyi magasságonként. Ez csökkenti az abszolút nyomást, és 1000 lábonként 3-4%-tel csökkentheti a hengerek teljesítményét, hacsak nem kompenzáljuk nyomásszabályozással.
Hogyan alakítja át a mérőnyomást abszolút nyomássá?
Adja hozzá a légköri nyomást a mérőnyomáshoz: PSIA = PSIG + légköri nyomás. A pontos átváltáshoz a helyi légköri nyomást (a magasságtól függően változik) használja a szabványos 14,7 PSI helyett.
Mi történik, ha abszolút nyomás számításánál a mérőnyomást használja?
Az abszolút nyomást igénylő képletekben a mérőnyomás használata a légköri nyomással arányos hibákat okoz - tengerszinten jellemzően 15%. Ezek a hibák alulméretezett berendezéseket és rossz rendszerteljesítményt okozhatnak.
A rúd nélküli palackoknál szükség van abszolút nyomásszámításra?
Igen, a rúd nélküli hengerek ugyanazokat a nyomásviszonyokat használják, mint a hagyományos hengerek. Az erőszámítások, az áramlás méretezése és a teljesítményelemzés mind az abszolút nyomásértékek előnyeit élvezik, különösen magassági vagy vákuumos alkalmazásokban.
-
Ismerje meg a rúd nélküli pneumatikus hengerek tervezési és működési előnyeit, amelyeket gyakran alkalmaznak az anyagmozgatásban és az automatizálásban. ↩
-
Fedezze fel az ideális gáztörvényt (PV=nRT), amely egy alapvető állapotegyenlet, amely leírja a gázok nyomása, térfogata és hőmérséklete közötti kapcsolatot. ↩
-
Ismerje meg az olyan abszolút hőmérsékleti skálákat, mint a Kelvin és a Rankine, és azt, hogy ezek miért nélkülözhetetlenek a termodinamikai és gáztörvény-számításokhoz. ↩
-
Értse a sűrítési arány jelentőségét a kompresszor teljesítményében, és azt, hogy hogyan kell kiszámítani az abszolút nyomás alapján. ↩
-
Fedezze fel, hogyan működnek a pneumatikus szállítórendszerek az ömlesztett anyagok sűrített gázzal történő szállítására az ipari folyamatokban. ↩




