
Avete mai notato misteriose vibrazioni nelle vostre linee pneumatiche? O inspiegabili variazioni di forza nei cilindri nonostante una pressione di alimentazione stabile? Questi fenomeni non sono casuali: sono il risultato di onde di pressione che si propagano nel sistema, creando effetti che possono variare da piccole inefficienze a guasti catastrofici.
Le fluttuazioni di pressione nei sistemi pneumatici sono fenomeni ondulatori che si propagano a velocità prossime alla velocità del suono1creando effetti dinamici, tra cui la risonanza, onde stazionarie2e l'amplificazione della pressione. La comprensione di queste fluttuazioni è fondamentale perché possono provocare l'affaticamento dei componenti, l'instabilità del controllo e l'aumento della pressione. perdite di energia di 10-25% in tipici sistemi industriali3.
Il mese scorso ho prestato la mia consulenza a uno stabilimento di assemblaggio automobilistico del Tennessee, dove un sistema di serraggio pneumatico critico presentava variazioni di forza intermittenti nonostante una pressione di alimentazione stabile. Il team di manutenzione aveva sostituito valvole, regolatori e persino l'intero sistema. unità di preparazione dell'aria4 senza successo. Analizzando la dinamica delle onde di pressione, in particolare i modelli di onde stazionarie nelle linee di alimentazione, abbiamo individuato che stavano operando a una frequenza che creava un'interferenza distruttiva sul cilindro. Un semplice aggiustamento della lunghezza della linea ha eliminato il problema, risparmiando settimane di ritardi nella produzione. Lasciate che vi mostri come la comprensione della teoria delle fluttuazioni di pressione possa trasformare l'affidabilità del vostro sistema pneumatico.
Indice dei contenuti
- Velocità di propagazione delle onde: A che velocità viaggiano le perturbazioni di pressione nel vostro sistema?
- Verifica delle onde stazionarie: In che modo le frequenze risonanti creano problemi di prestazioni?
- Metodi di attenuazione degli impulsi: Quali tecniche smorzano efficacemente le oscillazioni di pressione distruttive?
- Conclusione
- Domande frequenti sulle fluttuazioni di pressione nei sistemi pneumatici
Velocità di propagazione delle onde: A che velocità viaggiano le perturbazioni di pressione nel vostro sistema?
La comprensione della velocità di propagazione dei disturbi di pressione attraverso i sistemi pneumatici è fondamentale per prevederne e controllarne gli effetti. La velocità di propagazione determina il tempo di risposta del sistema, le frequenze di risonanza e il potenziale di interferenza distruttiva.
Le onde di pressione nei sistemi pneumatici viaggiano alla velocità del suono nel mezzo gassoso, che può essere calcolata con la formula c = √(γRT), dove γ è il rapporto di calore specifico, R è la costante specifica del gas e T è la temperatura assoluta. Per l'aria a 20°C, ciò equivale a circa 343 m/s, sebbene questa velocità sia modificata da fattori quali l'elasticità del tubo, la comprimibilità del gas e le condizioni di flusso.
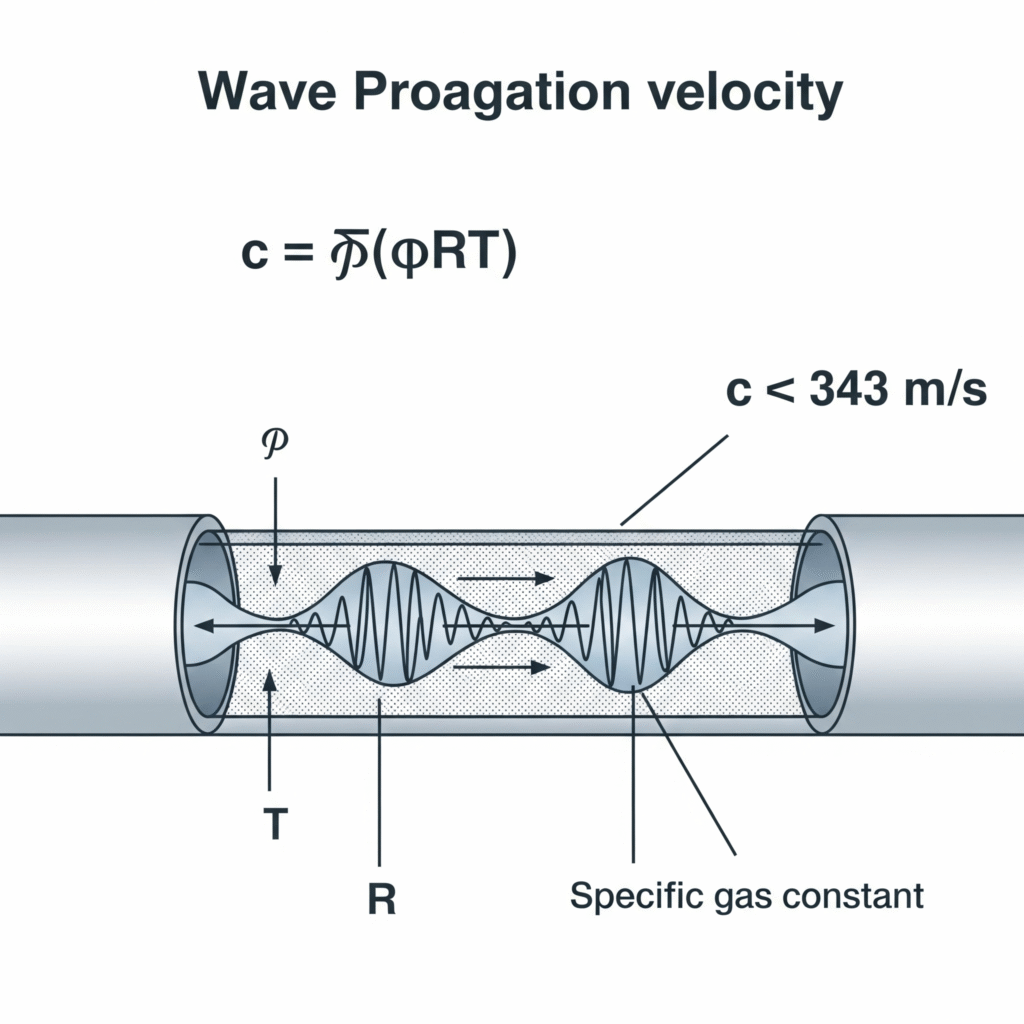
Di recente ho contribuito alla risoluzione dei problemi di una macchina di assemblaggio di precisione in Svizzera, dove le pinze pneumatiche registravano un ritardo di 12 ms tra l'attivazione e l'applicazione della forza, un'enormità in un ambiente di produzione ad alta velocità. I loro ingegneri avevano ipotizzato una trasmissione istantanea della pressione. Misurando l'effettiva velocità di propagazione delle onde nel loro sistema (328 m/s) e tenendo conto della lunghezza della linea di 4 metri, abbiamo calcolato un tempo di trasmissione teorico di 12,2 ms, quasi esattamente corrispondente al ritardo osservato. Avvicinando le valvole agli attuatori, il ritardo si è ridotto a 3 ms e la velocità di produzione è aumentata di 14%.
Equazioni di velocità dell'onda fondamentale
L'equazione di base per la velocità di propagazione delle onde di pressione in un gas è:
c = √(γRT)
Dove:
- c = Velocità di propagazione dell'onda (m/s)
- γ = Rapporto di calore specifico (1,4 per l'aria)
- R = costante specifica dei gas (287 J/kg-K per l'aria)
- T = Temperatura assoluta (K)
Per l'aria a 20°C (293K), si ottiene:
c = √(1,4 × 287 × 293) = 343 m/s
Velocità d'onda modificata nelle linee pneumatiche
Nei sistemi pneumatici reali, la velocità effettiva dell'onda è modificata dall'elasticità del tubo e da altri fattori secondo la formula:
c_eff = c / √(1 + (Dψ/Eh))
Dove:
- c_eff = Velocità effettiva dell'onda (m/s)
- D = Diametro del tubo (m)
- ψ = fattore di compressibilità del gas
- E = Modulo elastico del materiale del tubo (Pa)
- h = spessore della parete del tubo (m)
Effetti della temperatura e della pressione sulla velocità dell'onda
La velocità dell'onda varia in base alle condizioni operative:
| Temperatura | Pressione | Velocità d'onda nell'aria | Implicazioni pratiche |
|---|---|---|---|
| 0°C (273K) | 1 bar | 331 m/s | Risposta più lenta in ambienti freddi |
| 20°C (293K) | 1 bar | 343 m/s | Condizione di riferimento standard |
| 40°C (313K) | 1 bar | 355 m/s | Risposta più rapida in ambienti caldi |
| 20°C (293K) | 6 bar | 343 m/s* | La pressione ha un effetto diretto minimo sulla velocità |
*Nota: mentre la velocità d'onda di base è indipendente dalla pressione, la velocità effettiva nei sistemi reali può essere influenzata dalle variazioni indotte dalla pressione nell'elasticità del tubo e nel comportamento del gas.
Calcolo pratico del tempo di propagazione delle onde
Per un sistema pneumatico con:
- Lunghezza della linea (L): 5 metri
- Temperatura di esercizio: 20°C (c = 343 m/s)
- Materiale del tubo: Tubo in poliuretano (modifica la velocità di circa 5%)
La velocità effettiva delle onde sarebbe:
c_eff = 343 × 0,95 = 326 m/s
E il tempo di propagazione dell'onda sarebbe:
t = L/c_eff = 5/326 = 0,0153 secondi (15,3 millisecondi)
Questo rappresenta il tempo minimo necessario per una variazione di pressione da un'estremità all'altra della linea, un fattore critico nelle applicazioni ad alta velocità.
Tecniche di misurazione della velocità dell'onda
Per misurare la velocità effettiva delle onde nei sistemi pneumatici si possono utilizzare diversi metodi:
Metodo del doppio sensore di pressione
- Installare i sensori di pressione a distanze note
- Creare un impulso di pressione (apertura rapida della valvola)
- Misurare il ritardo tra l'aumento di pressione di ciascun sensore
- Calcolo della velocità come distanza divisa per il tempo di ritardo
Metodo della frequenza di risonanza
- Creare oscillazioni di pressione in un tubo chiuso
- Misurare la frequenza fondamentale di risonanza (f)
- Calcolare la velocità utilizzando c = 2Lf per un tubo chiuso.
- Verifica con le armoniche (multipli dispari della fondamentale)
Metodo di temporizzazione della riflessione
- Installare un sensore di pressione vicino a una valvola
- Creare un impulso di pressione aprendo rapidamente la valvola
- Misura del tempo tra l'impulso iniziale e l'impulso riflesso
- Calcolare la velocità come 2L diviso il tempo di riflessione
Caso di studio: Impatto della velocità d'onda sulla risposta del sistema
Per un dispositivo finale robotico con pinze pneumatiche:
| Parametro | Progetto originale (5 linee) | Design ottimizzato (linee da 1 m) | Miglioramento |
|---|---|---|---|
| Lunghezza della linea | 5 metri | 1 metro | Riduzione 80% |
| Tempo di propagazione dell'onda | 15,3 ms | 3,1 ms | 12,2 ms più veloce |
| Tempo di accumulo della pressione | 28 ms | 9 ms | 19 ms più veloce |
| Stabilità della forza di presa | Variazione ±12% | Variazione ±3% | Miglioramento 75% |
| Tempo di ciclo | 1,2 secondi | 0,95 secondi | 21% più veloce |
| Tasso di produzione | 3000 parti/ora | 3780 parti/ora | Aumento 26% |
Questo caso di studio dimostra come la comprensione e l'ottimizzazione della propagazione delle onde possa avere un impatto significativo sulle prestazioni del sistema.
Verifica delle onde stazionarie: In che modo le frequenze risonanti creano problemi di prestazioni?
Le onde stazionarie si verificano quando le onde di pressione si riflettono e interferiscono tra loro, creando schemi fissi di nodi e antinodi di pressione. Questi fenomeni di risonanza possono causare gravi problemi di prestazioni nei sistemi pneumatici se non vengono adeguatamente compresi e gestiti.
Le onde stazionarie nei sistemi pneumatici si verificano quando le onde di pressione si riflettono sui confini e interferiscono in modo costruttivo, creando frequenze di risonanza in cui le fluttuazioni di pressione vengono amplificate. Queste risonanze seguono la formula f = nc/2L per tubi chiusi, dove n è il numero armonico, c è la velocità dell'onda e L è la lunghezza del tubo. La verifica sperimentale attraverso sensori di pressione, accelerometri e misure acustiche conferma queste previsioni teoriche e guida strategie di mitigazione efficaci.
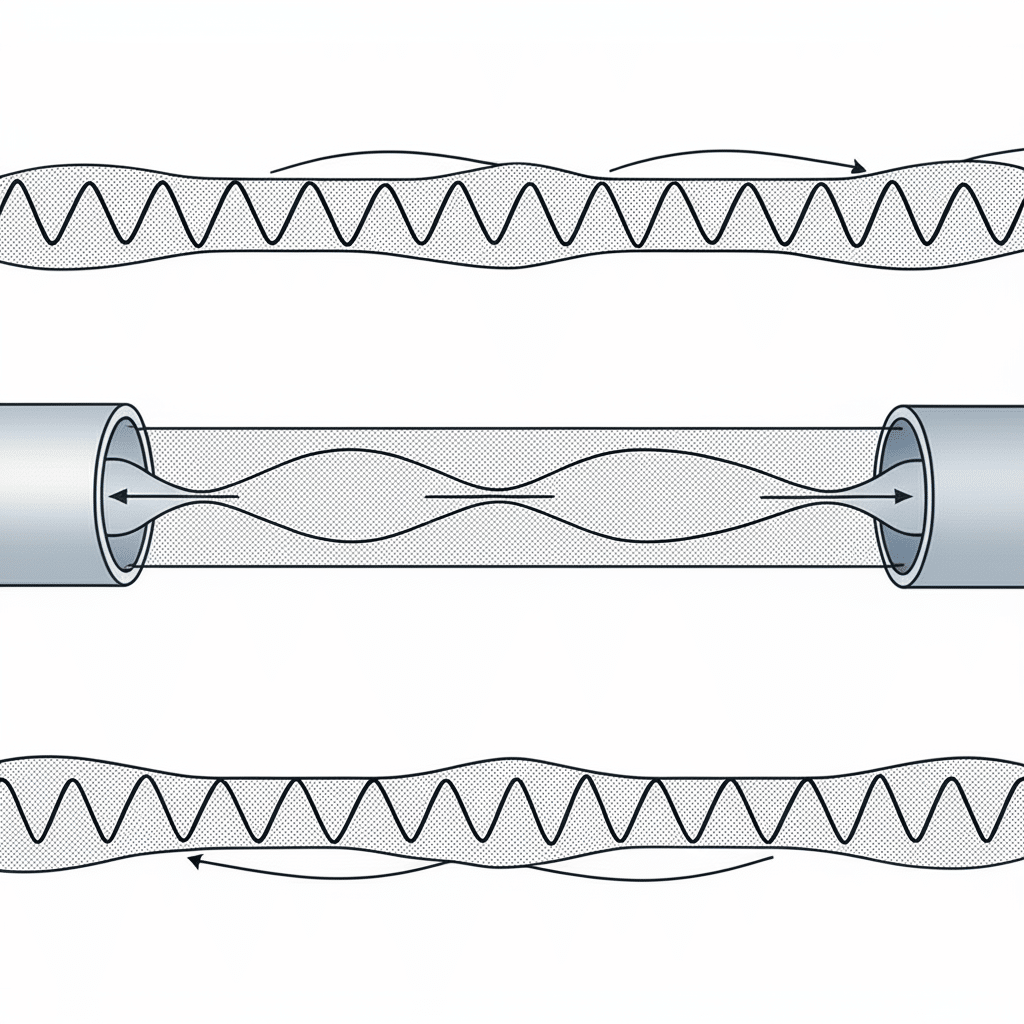
Durante un recente progetto con un produttore di dispositivi medici del Massachusetts, il loro sistema di posizionamento pneumatico di precisione presentava misteriose fluttuazioni di forza a frequenze operative specifiche. Conducendo test di verifica delle onde stazionarie, abbiamo identificato che la linea di alimentazione di 2,1 metri presentava una risonanza fondamentale a 81 Hz, che corrispondeva esattamente alla frequenza di ciclo dell'attuatore. Questa risonanza amplificava le fluttuazioni di pressione di 320%. Regolando la lunghezza della linea a 1,8 metri, abbiamo allontanato la frequenza di risonanza dal loro intervallo operativo e abbiamo eliminato completamente il problema, migliorando la precisione di posizionamento da ±0,8 mm a ±0,15 mm.
Fondamenti delle onde stazionarie
Le onde stazionarie si formano quando le onde incidenti e riflesse interferiscono, creando modelli fissi di nodi di pressione (fluttuazione minima) e antinodi (fluttuazione massima).
Le frequenze di risonanza di una linea pneumatica dipendono dalle condizioni al contorno:
Per una linea con estremità chiuse (più comune nei sistemi pneumatici):
f = nc/2L
Dove:
- f = frequenza di risonanza (Hz)
- n = Numero armonico (1, 2, 3, ecc.)
- c = Velocità dell'onda (m/s)
- L = Lunghezza della linea (m)
Per una linea con un'estremità aperta:
f = (2n-1)c/4L
Per una linea con entrambe le estremità aperte (raramente nella pneumatica):
f = nc/2L
Metodi di verifica sperimentale
Diverse tecniche possono verificare i modelli di onde stazionarie nei sistemi pneumatici:
Schiera di sensori di pressione multipli
- Installare i trasduttori di pressione a intervalli regolari lungo la linea pneumatica.
- Eccitare il sistema con una scansione di frequenza o un impulso.
- Registrare le fluttuazioni di pressione in ciascuna posizione
- Mappare l'ampiezza della pressione rispetto alla posizione per identificare nodi e antinodi.
- Confrontare le frequenze misurate con le previsioni teoriche
Correlazione acustica
- Utilizzare sensori acustici (microfoni) per rilevare il suono dalle fluttuazioni di pressione.
- Correlare l'intensità sonora alla frequenza operativa
- Identificare i picchi di intensità sonora corrispondenti alle frequenze di risonanza.
- Verificare che i picchi si verifichino alle frequenze previste
Misure dell'accelerometro
- Montaggio di accelerometri su linee e componenti pneumatici
- Misura dell'ampiezza delle vibrazioni in tutta la gamma di frequenze
- Identificare i picchi di risonanza nello spettro di vibrazione
- Correlazione con le frequenze delle onde stazionarie previste
Calcolo pratico della frequenza delle onde stazionarie
Per un tipico sistema pneumatico con:
- Lunghezza della linea (L): 3 metri
- Velocità dell'onda (c): 343 m/s
- Configurazione delle estremità chiuse
La frequenza fondamentale di risonanza sarebbe:
f₁ = c/2L = 343/(2×3) = 57,2 Hz
E le armoniche sarebbero:
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz
Queste frequenze rappresentano potenziali punti problematici in cui le fluttuazioni di pressione possono essere amplificate.
Modelli di onde stazionarie e loro effetti
| Armonico | Modello di nodo/antinodo | Effetti del sistema | Componenti critici interessati |
|---|---|---|---|
| Fondamentale (n=1) | Un antinodo di pressione al centro | Grandi variazioni di pressione sulla linea mediana | Componenti in linea, raccordi |
| Secondo (n=2) | Due antinodi, nodo al centro | Variazioni di pressione in prossimità delle estremità | Valvole, attuatori, regolatori |
| Terzo (n=3) | Tre antinodi, due nodi | Modello di pressione complesso | Componenti multipli del sistema |
| Quarto (n=4) | Quattro antinodi, tre nodi | Oscillazioni ad alta frequenza | Guarnizioni, piccoli componenti |
Studio di caso di verifica sperimentale
Per un sistema di posizionamento pneumatico di precisione che presenta prestazioni incoerenti:
| Parametro | Previsione teorica | Misura sperimentale | Correlazione |
|---|---|---|---|
| Frequenza fondamentale | 81,2 Hz | 79,8 Hz | 98.3% |
| Seconda armonica | 162,4 Hz | 160,5 Hz | 98.8% |
| Terza Armonica | 243,6 Hz | 240,1 Hz | 98.6% |
| Amplificazione della pressione | 3:1 alla risonanza (stima) | 3,2:1 alla risonanza (misurato) | 93.8% |
| Posizioni dei nodi | 0, 1,05, 2,1 metri | 0, 1,08, 2,1 metri | 97.2% |
Questo caso di studio dimostra l'eccellente accordo tra le previsioni teoriche e le misure sperimentali dei fenomeni di onde stazionarie.
Implicazioni pratiche delle onde stazionarie
Le onde stazionarie creano diversi problemi significativi nei sistemi pneumatici:
Amplificazione della pressione
- Le fluttuazioni possono essere amplificate da 3 a 5 volte alla risonanza.
- Può superare i valori nominali di pressione dei componenti
- Crea variazioni di forza negli attuatoriFatica dei componenti
- I cicli di pressione ad alta frequenza accelerano l'usura delle tenute
- Le vibrazioni causano l'allentamento dei raccordi e le perdite
- Riduce la durata del sistema di 30-70% nei casi più graviInstabilità del controllo
- I sistemi a retroazione possono oscillare a frequenze di risonanza.
- Il controllo della posizione e della forza diventa imprevedibile
- Può creare oscillazioni auto-rinforzantiPerdite di energia
- Le onde stazionarie rappresentano energia intrappolata
- Può aumentare il consumo di energia di 10-30%
- Riduce l'efficienza complessiva del sistema
Metodi di attenuazione degli impulsi: Quali tecniche smorzano efficacemente le oscillazioni di pressione distruttive?
Il controllo delle fluttuazioni di pressione è essenziale per un funzionamento affidabile del sistema pneumatico. Per ridurre o eliminare le oscillazioni di pressione problematiche, si possono utilizzare vari metodi di attenuazione.
L'attenuazione degli impulsi di pressione nei sistemi pneumatici può essere ottenuta con diversi metodi: camere volumetriche che assorbono l'energia attraverso la compressione del gas, elementi restrittivi che creano smorzamento attraverso effetti viscosi, risonatori accordati che annullano frequenze specifiche e sistemi di cancellazione attiva che generano controimpulsi. Per ottenere un'attenuazione efficace è necessario adattare il metodo al contenuto di frequenza specifico e all'ampiezza delle fluttuazioni di pressione.
Di recente ho lavorato con un produttore di apparecchiature per l'imballaggio dell'Illinois il cui sistema pneumatico ad alta velocità era soggetto a forti fluttuazioni di pressione che causavano forze di tenuta incoerenti. I loro ingegneri avevano provato a utilizzare serbatoi riceventi di base senza successo. Attraverso un'analisi dettagliata degli impulsi di pressione, abbiamo individuato che il sistema presentava diverse componenti di frequenza che richiedevano approcci di attenuazione diversi. Implementando una soluzione ibrida che combina un Risonatore di Helmholtz5 sintonizzati sulla loro oscillazione dominante di 112 Hz e una serie di orifizi di restrizione, abbiamo ridotto le fluttuazioni di pressione di 94% ed eliminato completamente le incongruenze di tenuta.
Meccanismi di attenuazione fondamentali
Per attenuare gli impulsi di pressione si possono utilizzare diversi meccanismi fisici:
Attenuazione basata sul volume
Funziona grazie alla comprimibilità del gas:
- Fornisce un elemento di conformità che assorbe l'energia di pressione.
- Più efficace per le fluttuazioni a bassa frequenza
- Implementazione semplice con una caduta di pressione minima
Attenuazione basata sulla restrizione
Funziona attraverso la dissipazione viscosa:
- Converte l'energia della pressione in calore attraverso l'attrito.
- Efficace in un'ampia gamma di frequenze
- Crea una caduta di pressione permanente
Attenuazione basata su risonatori
Funziona attraverso un'interferenza distruttiva sintonizzata:
- Annulla le componenti di frequenza specifiche
- Altamente efficace per frequenze mirate
- Impatto minimo sul flusso allo stato stazionario
Attenuazione basata sui materiali
Funziona attraverso la flessibilità e lo smorzamento delle pareti:
- Assorbe l'energia attraverso la deformazione delle pareti
- Fornisce un'attenuazione a banda larga
- Può essere integrato nei componenti esistenti
Principi di progettazione della camera di volume
Le camere di volume (serbatoi di ricezione) sono i dispositivi di attenuazione più comuni:
L'efficacia di una camera volumetrica dipende dal rapporto tra volume della camera e volume della linea:
Rapporto di attenuazione = 1 + (Vc/Vl)
Dove:
- Vc = Volume della camera
- Vl = Volume della linea
Per l'analisi in funzione della frequenza, il rapporto di trasmissione è:
TR = 1/√(1 + (ωVc/Zc)²)
Dove:
- ω = frequenza angolare (2πf)
- Zc = Impedenza caratteristica della linea
Attenuazione dell'elemento restrittivo
Orifizi, materiali porosi e passaggi lunghi e stretti creano un'attenuazione per effetto viscoso:
La caduta di pressione attraverso una restrizione è la seguente:
ΔP = k(ρv²/2)
Dove:
- k = coefficiente di perdita
- ρ = densità del gas
- v = Velocità
L'attenuazione fornita aumenta con:
- Maggiore velocità del flusso
- Maggiore lunghezza della restrizione
- Diametro di passaggio ridotto
- Percorso di flusso più tortuoso
Sistemi di attenuazione con risonatore
I risonatori sintonizzati forniscono un'attenuazione di frequenza mirata:
Risonatore di Helmholtz
Camera di volume con collo stretto, sintonizzata su una frequenza specifica:
f = (c/2π)√(A/VL)
Dove:
- f = frequenza di risonanza
- c = velocità del suono
- A = Area della sezione trasversale del collo
- V = Volume della camera
- L = Lunghezza effettiva del collo
Risonatore a quarto d'onda
Un tubo di lunghezza specifica aperto a un'estremità:
f = c/4L
Dove:
- L = Lunghezza del tubo
Risonatori a branca laterale
Rami multipli sintonizzati per contenuti di frequenza complessi:
- Ogni ramo si rivolge a una frequenza specifica
- Può trattare più armoniche contemporaneamente
- Impatto minimo sul percorso principale del flusso
Sistemi di cancellazione attiva
Sistemi avanzati che generano controimpulsi:
Fase di rilevamento
- Rilevare le onde di pressione in arrivo
- Analizzare il contenuto di frequenza e l'ampiezzaFase di lavorazione
- Calcolo del segnale di cancellazione richiesto
- Tenere conto delle dinamiche e dei ritardi del sistemaFase di attuazione
- Generare onde di contropressione
- Tempo preciso per l'interferenza distruttiva
Confronto delle prestazioni di attenuazione
| Metodo | Bassa frequenza (<50 Hz) | Media frequenza (50-200 Hz) | Alta frequenza (>200 Hz) | Caduta di pressione | Complessità |
|---|---|---|---|---|---|
| Camera di volume | Eccellente (>90%) | Moderato (40-70%) | Scarso (<30%) | Molto basso | Basso |
| Orifizio restrittivo | Scarso (<30%) | Buono (60-80%) | Eccellente (>80%) | Alto | Basso |
| Risonatore di Helmholtz | Scarsa risonanza esterna | Eccellente alla risonanza | Scarsa risonanza esterna | Basso | Medio |
| Tubo a quarto d'onda | Scarsa risonanza esterna | Eccellente alla risonanza | Scarsa risonanza esterna | Basso | Medio |
| Risonatori multipli | Moderato (40-60%) | Eccellente (>80%) | Buono (60-80%) | Basso | Alto |
| Cancellazione attiva | Eccellente (>90%) | Eccellente (>90%) | Buono (70-85%) | Nessuno | Molto alto |
| Sistemi ibridi | Eccellente (>90%) | Eccellente (>90%) | Eccellente (>90%) | Moderato | Alto |
Implementazione pratica dell'attenuazione
Per un'efficace attenuazione degli impulsi di pressione:
Caratterizzare le fluttuazioni
- Misurare il contenuto di ampiezza e frequenza
- Identificare le frequenze dominanti
- Determinare se è necessario attenuare la banda larga o frequenze specifiche.Selezionare i metodi appropriati
- Per le basse frequenze: Camere di volume
- Per frequenze specifiche: Risonatori accordati
- Per l'attenuazione a banda larga: Limitazioni o approcci ibridi
- Per applicazioni critiche: Cancellazione attivaOttimizzare il posizionamento
- Vicino alle sorgenti per evitare la propagazione
- Vicino ai componenti sensibili per proteggerli
- In posizioni strategiche per rompere i modelli di onde stazionarieVerifica delle prestazioni
- Misura prima/dopo l'attenuazione
- Confermare le condizioni di funzionamento
- Garantire l'assenza di conseguenze indesiderate
Caso di studio: Attenuazione multimetodo nel confezionamento ad alta velocità
Per un sistema di tenuta pneumatico ad alta velocità soggetto a fluttuazioni di pressione:
| Parametro | Prima dell'attenuazione | Dopo la Camera di volume | Dopo la soluzione ibrida | Miglioramento |
|---|---|---|---|---|
| Bassa frequenza (<50 Hz) | ±0,8 bar | ±0,12 bar | ±0,05 bar | Riduzione 94% |
| Media frequenza (112 Hz) | ±1,2 bar | ±0,85 bar | ±0,07 bar | Riduzione 94% |
| Alta frequenza (>200 Hz) | ±0,4 bar | ±0,36 bar | ±0,04 bar | Riduzione 90% |
| Variazione della forza di tenuta | ±28% | ±22% | ±2,5% | Miglioramento 91% |
| Tasso di rifiuto dei prodotti | 4.2% | 3.1% | 0.3% | Riduzione 93% |
| Efficienza del sistema | Linea di base | +4% | +12% | Miglioramento 12% |
Questo caso di studio dimostra come un approccio mirato e multimetodo all'attenuazione possa migliorare notevolmente le prestazioni del sistema.
Tecniche di attenuazione avanzate
Per applicazioni particolarmente impegnative:
Attenuazione distribuita
Utilizzo di più dispositivi di piccole dimensioni piuttosto che di uno grande:
- L'attenuazione è più vicina alle sorgenti e ai componenti sensibili.
- Rompe in modo più efficace i modelli di onde stazionarie
- Fornisce ridondanza e prestazioni più costanti
Smorzamento selettivo in frequenza
Mirate a frequenze problematiche specifiche:
- Utilizza risonatori multipli sintonizzati su frequenze diverse
- Conserva la risposta desiderata del sistema eliminando i problemi
- Riduce al minimo l'impatto sulle prestazioni complessive del sistema
Sistemi adattivi
Regolazione dell'attenuazione in base alle condizioni operative:
- Utilizza sensori per monitorare le fluttuazioni di pressione.
- Regola automaticamente i parametri di attenuazione
- Ottimizza le prestazioni in condizioni diverse
Conclusione
La comprensione della teoria delle fluttuazioni di pressione, della velocità di propagazione delle onde, della verifica delle onde stazionarie e dei metodi di attenuazione degli impulsi, fornisce le basi per una progettazione affidabile ed efficiente dei sistemi pneumatici. Applicando questi principi, è possibile eliminare misteriosi problemi di prestazioni, prolungare la durata dei componenti e migliorare l'efficienza del sistema, garantendo un funzionamento costante in tutte le condizioni operative.
Domande frequenti sulle fluttuazioni di pressione nei sistemi pneumatici
In che modo le fluttuazioni di pressione influiscono sulla durata dei componenti pneumatici?
Le fluttuazioni di pressione riducono significativamente la durata dei componenti attraverso diversi meccanismi: causano un'usura accelerata delle guarnizioni creando micromovimenti sulle superfici di tenuta; inducono l'affaticamento dei materiali nei diaframmi e negli elementi flessibili attraverso cicli di sollecitazione ripetuti; favoriscono l'allentamento delle connessioni filettate a causa delle vibrazioni; creano concentrazioni di sollecitazioni localizzate in corrispondenza delle transizioni geometriche. I sistemi con forti fluttuazioni di pressione incontrollate hanno in genere una vita dei componenti 40-70% più breve rispetto ai sistemi correttamente smorzati, e le guarnizioni e i diaframmi sono particolarmente vulnerabili.
Qual è la relazione tra la lunghezza della linea e il tempo di risposta alla pressione nei sistemi pneumatici?
La lunghezza della linea influisce direttamente sul tempo di risposta alla pressione secondo una semplice relazione: il tempo di risposta aumenta linearmente con la lunghezza della linea a un tasso determinato dalla velocità di propagazione dell'onda. Per l'aria in condizioni standard (velocità dell'onda ≈ 343 m/s), ogni metro di linea aggiunge circa 2,9 millisecondi di ritardo nella trasmissione. Tuttavia, il tempo effettivo di formazione della pressione è in genere da 2 a 5 volte superiore al tempo iniziale di trasmissione dell'onda, a causa della necessità di riflessioni multiple per equalizzare la pressione. Ciò significa che una linea di 5 metri potrebbe avere un tempo di trasmissione dell'onda di 14,5 ms, ma un tempo di accumulo della pressione di 30-70 ms.
Come posso identificare se il mio sistema pneumatico è soggetto a fluttuazioni di pressione risonante?
Le fluttuazioni di pressione risonanti si manifestano tipicamente attraverso diversi sintomi osservabili: i componenti vibrano a frequenze operative specifiche ma non ad altre; le prestazioni del sistema variano in modo incoerente con piccole variazioni delle condizioni operative; si sente un "canto" o un "fischio" dalle linee pneumatiche; i manometri mostrano letture oscillanti; le prestazioni degli attuatori (velocità, forza) variano ciclicamente. Per confermare la risonanza, misurate la pressione in diversi punti del sistema utilizzando trasduttori a risposta rapida (tempo di risposta <1ms) e cercate modelli di onde stazionarie in cui l'ampiezza della pressione varia con la posizione lungo la linea.
Le fluttuazioni di pressione influiscono sull'efficienza energetica dei sistemi pneumatici?
Le fluttuazioni di pressione hanno un impatto significativo sull'efficienza energetica, riducendola in genere di 10-25% attraverso diversi meccanismi: aumentano i tassi di perdita creando pressioni di picco più elevate; sprecano energia nella compressione e nell'espansione cicliche; causano un aumento dell'attrito nei componenti a causa delle vibrazioni; e spesso inducono gli operatori ad aumentare la pressione di alimentazione per compensare i problemi di prestazioni. Inoltre, la turbolenza e la separazione del flusso create dalle fluttuazioni di pressione convertono l'energia utile della pressione in calore disperso. Una corretta attenuazione delle fluttuazioni di pressione può migliorare l'efficienza del sistema di 5-15% senza altre modifiche.
In che modo le variazioni di temperatura influenzano il comportamento delle onde di pressione nei sistemi pneumatici?
La temperatura influisce in modo significativo sul comportamento delle onde di pressione attraverso diversi meccanismi: influisce direttamente sulla velocità di propagazione delle onde (circa +0,6 m/s per ogni aumento di °C); cambia la densità e la viscosità del gas, alterando le caratteristiche di smorzamento; modifica le proprietà elastiche delle linee pneumatiche, influenzando la riflessione e la trasmissione delle onde; e sposta le frequenze di risonanza (circa +0,17% per °C). Questa sensibilità alla temperatura significa che un sistema che funziona perfettamente a 20°C può presentare risonanze problematiche quando opera a 40°C, o che i dispositivi di attenuazione tarati per le condizioni invernali possono essere inefficaci in estate.
-
Fornisce una spiegazione dettagliata della fisica che sta alla base della velocità del suono, di come viene calcolata e dei fattori che la influenzano. ↩
-
Offre una comprensione fondamentale dei fenomeni delle onde stazionarie, compreso il modo in cui si formano dall'interferenza e le loro caratteristiche principali, come i nodi e gli antinodi. ↩
-
Fornisce prove e studi di settore che verificano la gamma tipica di perdite energetiche causate da inefficienze come le fluttuazioni di pressione nei sistemi pneumatici. ↩
-
Spiega i componenti e il funzionamento di un'unità di preparazione dell'aria (FRL), essenziale per mantenere la qualità dell'aria nei sistemi pneumatici. ↩
-
Offre una spiegazione approfondita dei principi alla base di un risonatore di Helmholtz, un dispositivo fondamentale per l'attenuazione mirata delle frequenze nei sistemi acustici e fluidi. ↩


